自动驾驶汽车测试场景基元自动提取方法*

朱 冰，孙宇航，赵 健，张培兴，范天昕，宋东鉴

（吉林大学，汽车仿真与控制国家重点实验室，长春 130022）

前言

准确可靠的测试技术是自动驾驶汽车安全上路的重要保障［1］，但海量测试里程、超长测试周期等因素导致传统基于里程的测试手段不再适用于自动驾驶汽车，基于场景的测试方法成为当前的研究热点［2］。

自然驾驶数据库是测试场景的重要来源之一。最传统的场景化测试方法是研究人员根据测试场景类型和定义，从自然驾驶数据库中手动和主观地提取感兴趣的特定测试场景，对汽车进行测试［3］。然而，随着自动驾驶汽车智能化等级的提高，相机、毫米波雷达、激光雷达、GPS、V2X等先进环境感知设备提供了丰富的交通场景信息，自然驾驶数据库的数据长度和维度爆炸式增长，通过手工提取测试场景不仅费时费力［4］，并且难以满足测试场景的覆盖性。

对自然驾驶数据库中的场景序列进行抽象和聚类是测试场景提取的基础。Li等［5］通过自编码器和k-means聚类方法，将自然驾驶数据库中的测试场景分成了4类。Lenard等［6］针对9 360例汽车与行人碰撞事故，应用系统聚类分析，挖掘出能够代表86%事故案例的6类典型逻辑场景。但是，交通场景具有复杂性和不确定性，一段场景序列可能包含多种行驶特征，直接对自然驾驶场景序列进行聚类会降低聚类的典型性和准确性。因此，需要根据场景序列中主车、交通参与者等动态要素的运动特征对场景序列进行基元提取。

场景基元是自然驾驶场景序列中有限的、不重叠的、时间连续的子集，是场景序列的基础组成部分，不同种类的场景基元反映了场景序列中要素之间的不同特性，例如：主车加速且前车减速、主车加速且前车匀速场景子序列分别代表两种不同类型的场景基元。

通过规则判断的方法可以对场景基元进行提取划分［7-9］。Kilicarslan等［8］分析了车载相机传感器中视频流信息的运动发散特征，制定了复杂的判定规则，从而从图像数据中识别判定安全、危险和碰撞3种场景。但是基于规则的方法不可避免会引入主观规则和阈值设置，不仅对不同的自然驾驶数据库不具有通用性，并且结果包含主观误差。Wang等［10］采用黏性层次狄利克雷过程-隐马尔科夫模型（sticky hierarchical Dirichlet process hidden Markov model，Sticky HDP-HMM）自动提取跟车场景序列的场景基元，但是Sticky HDP-HMM模型中车辆的运动特征独立性与场景基元持续时间具有耦合性，并且模型采用的多维高斯分布难以精确描述车辆运动状态在时间维度的变化，导致场景基元的可解释性和合理性相对较差。

针对上述问题，本文中提出基于解耦黏性-层次狄利克雷过程-隐马尔科夫模型（disentangled sticky hierarchical Dirichlet process hidden Markov model，DS-HDP-HMM）的自然驾驶数据库场景基元自动提取方法。以隐马尔科夫模型（hidden Markov model，HMM）作为框架，将车辆的运动状态视为隐马尔科夫过程，并采用向量自回归模型（vector autoregressive process，VAR）作为隐马尔科夫模型的观测概率分布函数，描述车辆运动状态与隐马尔科夫模型隐状态之间的映射关系；将自然驾驶数据库的多维场景时间序列作为隐马尔科夫模型的观测序列，作为模型的输入；将隐马尔科夫模型的隐状态作为模型的输出，不同的隐状态类型代表不同类型的场景基元。为了实现隐马尔科夫模型的求解，采用层次狄利克雷过程（hierarchical Dirichlet process，HDP）为隐马尔科夫模型提供先验分布和后验更新方法，采用解耦过程和黏性过程抑制隐马尔科夫模型隐状态的频繁切换。最后，采用HighD自然驾驶数据库对算法进行验证。

1 测试场景基元提取方法

本文中提出的DS-HDP-HMM方法的架构如图1所示，将车辆的运动状态视为隐马尔科夫过程。观测序列Y={y1，y2，y3，…}为自然驾驶数据库中的一段车辆运动状态序列，其中yt∈R1×d，yt为t时刻的观测向量，表示由前车相对距离、主车速度等组成的d维车辆状态向量。模型输出为隐状态序列，Z={z1，z2，z3，…}，zt为t时刻的隐状态，表示观测向量对应的场景基元类型。求解HMM模型首先需要确定模型的初始状态概率向量α、状态转移概率矩阵π和观测概率分布函数的参数θ等模型参数。为了准确表征车辆的运动状态，采用VAR模型作为隐马尔科夫模型的观测概率分布函数。为了实现HMM模型的求解，本文中基于贝叶斯理论采用HDP赋予模型参数先验分布和后验更新方法，并加入解耦过程和黏性过程抑制隐状态的频繁切换，通过吉布斯（Gibbs）采样方法对模型参数进行迭代更新，得到隐状态序列Z，将隐状态zt相同的观测向量yt标记为相同类型的场景基元。自然驾驶数据库中每一段场景序列都由一个或多个场景基元构成。

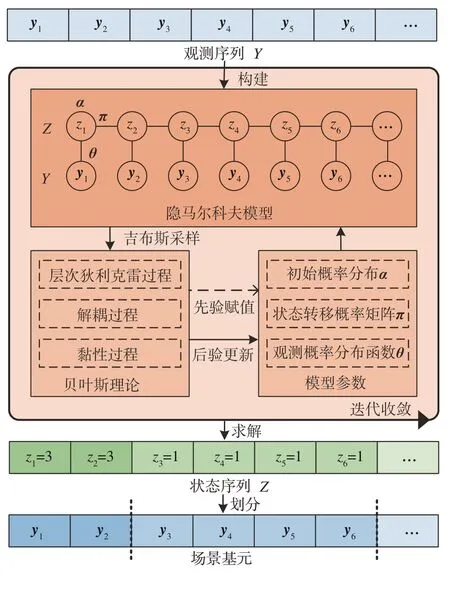
图1 DS-HDP-HMM整体流程示意图

1.1 隐马尔可夫模型

隐马尔可夫模型（HMM）描述通过马尔可夫链生成不可观测的状态随机序列，再由各个状态生成观测随机序列的过程［11］。隐马尔可夫模型由初始状态概率向量、状态转移概率矩阵和观测概率分布函数确定。

给定一个测试场景的车辆运动状态序列Y=Y∈Rd×T，构建HMM模型，观测概率分布函数 参 数 集 合 为隐状态序列为Z=其中zt=k，表示在t时刻的隐状态zt对应第k类观测概率分布函数，其参数为θk。

定义初始状态概率向量a为t=1时刻状态z1=k的概率：

式中ak=P(z1=k)，k=1，2，…，K。

定义状态转移概率矩阵中每个元素πzt-1，zt表示隐状态在t-1时刻处于zt-1的条件下在t时刻转移到zt的概率。则可以得到隐状态zt-1下一时刻的状态转移概率向量：

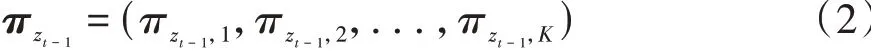
定义观测概率分布函数F(θzt)为向量自回归模型，模型由两个参数矩阵[ ]A，Σ确 定，即θzt=

因此，隐马尔可夫模型可简化描述为

1.2 解耦黏性层次狄利克雷模型

自然驾驶数据库场景复杂多变，难以穷尽。隐马尔科夫模型的初始状态概率向量α、状态转移概率矩阵π和观测概率分布函数的参数θ难以确定。本文中引入层次狄利克雷过程（HDP）为HMM模型参数提供先验分布和后验更新方法。

狄利克雷过程（Dirichlet process，DP）是一种应用于非参数贝叶斯模型的随机过程［12-13］，表示为

式（4）的含义为：G服从由基分布H和集中参数γ组成的狄利克雷过程。其Stick-breaking构造表示为

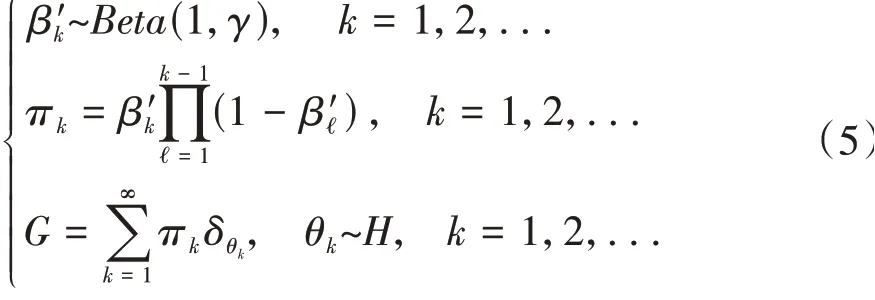
式中δθ是θ点的概率测度。通常用β～GEM(γ)表示权重系数的构造关系。

HDP是对DP的层次性拓展。首先，以基分布H和集中参数γ构造DP模型，G0～DP(γ，H)。然后以G0为基分布，以α0为集中参数，对每一组数据构造狄利克雷混合模型，Gj～DP(α0，G0)。

HDP-HMM模型在特征提取、模式识别、状态预测等方面［14-15］已经得到了广泛的应用，但是当HDPHMM模型应用于自然驾驶数据库场景基元提取时，很容易引起模型隐状态的快速频繁切换［13］，导致提取的场景基元时序过短，难以应用。状态转移概率矩阵π的特性对隐状态zt转换有很大影响，从而影响场景基元序列的时序长度。文献［16］中分析了状态转移概率矩阵π的3点特征：（1）状态转移概率矩阵每行值与基分布H的相似性；（2）状态转移概率矩阵对角线元素均值的大小；（3）状态转移概率矩阵对角线元素的相似性。

其中，HDP-HMM模型通过集中参数α0只能实现对特征1的控制，然而状态转移矩阵对角线元素反映了隐状态自转移的概率，模型无法对特征2和特征3的控制导致了隐状态的快速频繁切换。黏性HDP-HMM模型［17］是对其的改进，通过加入一个p参数，实现p∕(α0+p)参数控制特征2，(α0+p)参数同时控制特征1和特征3。考虑到在自然驾驶数据库中，不同的场景基元的车辆运动特性具有较高的独立性，特征1较大，而不同场景基元的持续时间不尽相同，特征3较小。为了实现特征1和特征3的解耦，本文采用了解耦黏性-层次狄利克雷-隐马尔科夫模型（DS-HDP-HMM）进行场景基元的提取。相比于HDP-HMM模型，DS-HDP-HMM模型增加两个超参数ρ1、ρ2，如图2所示，在相邻时间序列下，模型表示为

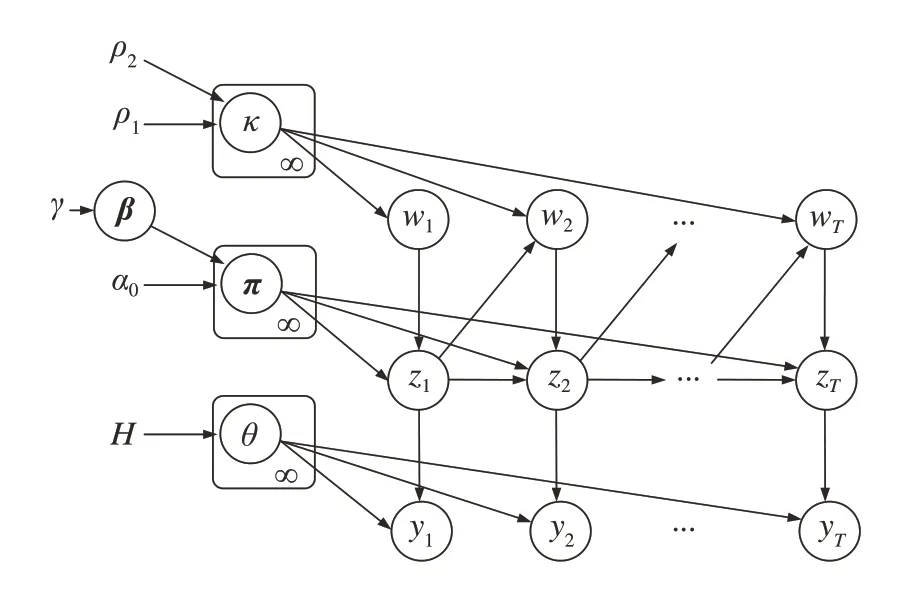
图2 DS-HDP-HMM模型结构示意图

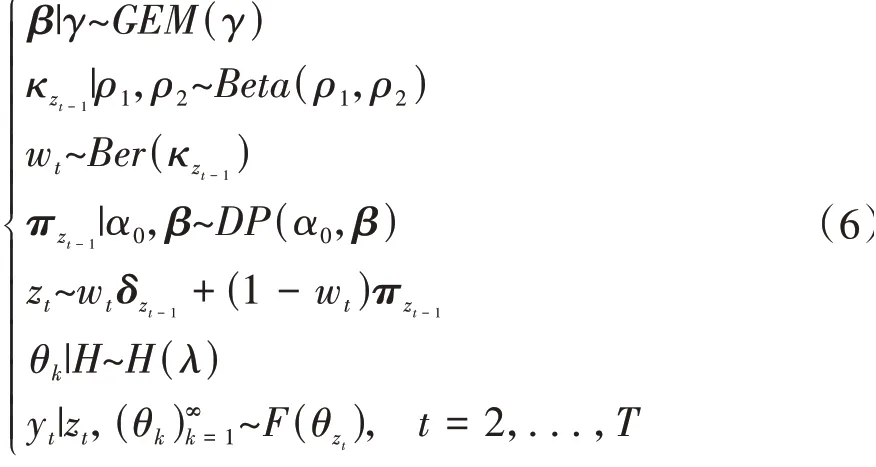
式中：δzt-1为第zt-1个元素为1、其余元素为0的向量；超参数ρ1、ρ2为状态自转移概率κzt-1的控制端参数；超参数γ、a0为集中参数，反映了状态转移概率πzt-1与基分布的相似性；超参数λ为基分布H的参数，基分布H表示VAR模型的参数分布；参数β、κzt-1、wt为中间变量。

1.3 向量自回归模型

目前场景基元提取所用的观测概率分布函数大多采用多维高斯分布［10］，计算复杂度较低，但是难以精确描述车辆运动状态变化，降低了场景基元提取的准确性。本文中引入向量自回归模型（VAR）作为观测概率分布函数。VAR模型认为当前时刻的观测向量与过去时刻的观测向量线性相关，VAR模型不仅适用于描述机动车辆的运动状态变化［18］，并且与隐马尔科夫模型的假设有较好的一致性。VAR(r)模型可表示为

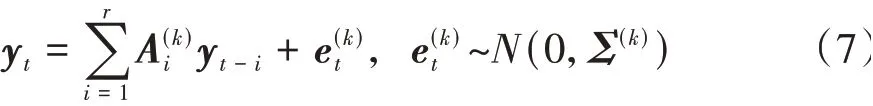
式中r为历史时刻的步长数量。考虑到在离散时间下，汽车t时刻的相对位置xt可以近似表征为

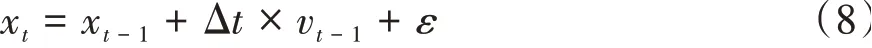
式中：xt-1表示t-1时刻的相对位置观测值；vt-1表示t-1时刻的相对速度观测值；Δt表示离散步长；ε表示误差值。式（8）与式（7）具有一致的表征形式，其它观测维度也类似，所以VAR模型适用于描述车辆的运动状态。

定义{t1，...，tNk}={t|zt=k}，Nk表示属于第k类场景基元的离散时刻数量。将式（7）写成矩阵的形式：

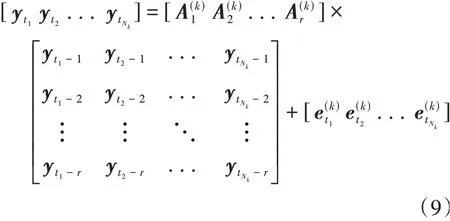
式（9）可以简写为

从式（10）可以看出，A(k)和Σ(k)为VAR（r）模型的核心参数，反映了车辆的运动状态。需要对参数{A(k)，Σ(k)}进行先验赋值和后验更新，其共轭先验分布为矩阵正态-逆威沙特（matrix-normal inverse-Wishart）分布［19］。在给定参数Σ(k)下参数A(k)∈Rd×m的矩阵正态分布先验MN(A(k)；M，Σ(k))为

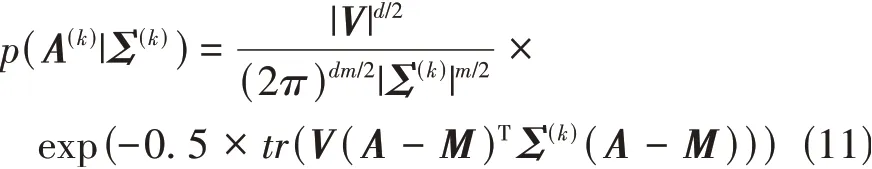
式中：M为均值矩阵，M∈Rd×m；Σ(k)为按行计算的协方差矩阵，Σ(k)∈Rd×d；V-1为按列计算的协方差矩阵，V-1∈Rm×m。设置初始参数为：M=0，V=Im×m。

参数Σ(k)的逆威沙特分布先验IW(S0，n0)为

式 中Γd(·)为 多 元 伽 马 函 数（multivariate Gamma function）。设 置 初 始 参 数 为：n0=d+2，S0=

在给定参数Σ(k)下参数A(k)的后验为

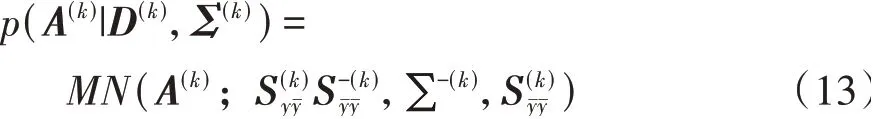
其中

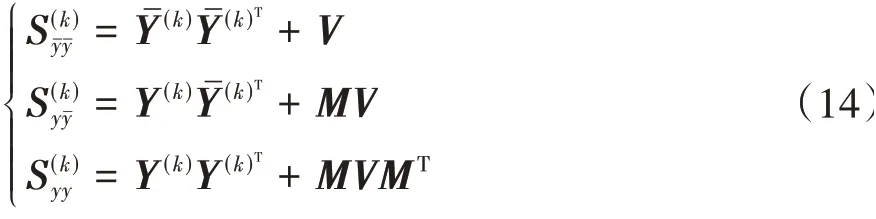
参数Σ(k)的后验为

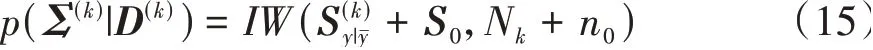
其中

1.4 模型初始化和后验更新

本节介绍DS-HDP-HMM模型关键参数的后验更新规则，但是其规则具有高度的抽象性，学者们巧妙地采用中国餐馆过程（Chinese restaurant franchise，CRF）［12-13］表征变量的含义及变量之间的关系。

CRF由多家餐厅构成，如图3所示，每家餐厅包含多张桌子，所有餐厅公用相同的菜单，用符号j表示餐厅序号，符号q表示餐桌序号，符号k表示菜品序号。菜单象征观测概率分布函数参数集合θ*，菜品序号k象征从观测概率分布函数参数集合θ*中取第k个参数θk。餐厅j与菜品k组成的方阵象征状态转移概率矩阵，表示在t-1时刻处于状态j在t时刻转移到状态k的概率。客人象征不同时刻的观测值yt。客人想点的菜品象征不同时刻观测值yt对应的观测概率分布函数的参数ϕt，定义每张桌子只有一道菜ψjq，一个餐馆不同桌子菜品可以相同，所以一张桌子的多位客人ϕt对应一个ψjq，不同桌子的菜品ψjq可以对应一个θk。新增统计变量mjk表示第j个餐厅里所有享用第k道菜的餐桌数，njk表示第j个餐厅享用第k道菜的所有客人总数，njqk表示第j个餐厅第q张餐桌上享用第k道菜的人数，“.”表示全部。DSHDP-HMM模型的变量更新要遵循中国餐馆过程。

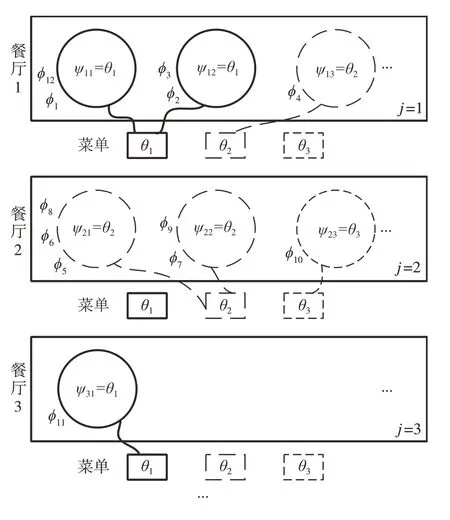
图3 CRF构造示意图

首先，根据DS-HDP-HMM模型定义（即式（6））初始化CRF模型。然后，计算模型参数的后验分布。

因为二项分布b(n，θ)的成功概率θ的共轭先验分布为贝塔分布，所以κ的后验概率满足：

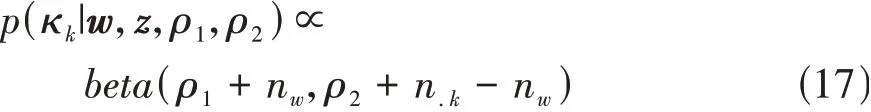
根据图2所示的DS-HDP-HMM模型结构示意图，nw为第k类场景基元对应的隐状态中wt=1的数量。n.k为第k类场景基元对应的隐状态数量。

β的后验概率为

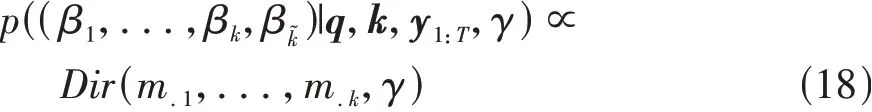
π的后验概率为

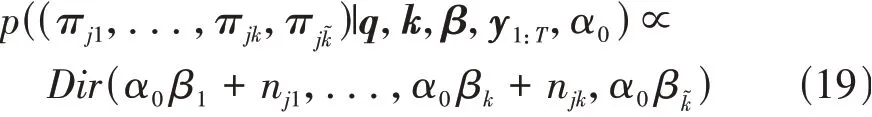
q的后验概率为

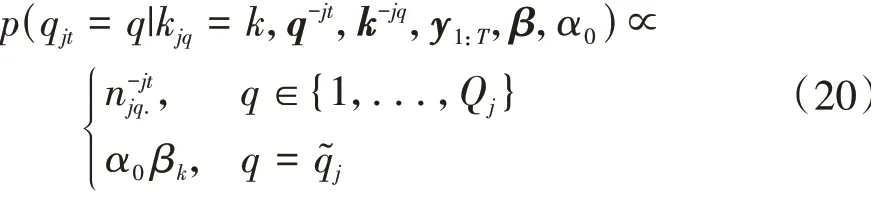
式中：Qj表示第j个餐馆的桌子总数表示在第j个餐馆第q张桌子除了第t位客人外的人数；q-jt表示除了第j个餐馆第t位客人外的餐桌分配；k-jq表示除了第j个餐馆第q张餐桌外的菜品分配。

m的后验概率可以通过对餐桌q后验概率的数学统计得出，即mjk为在j餐馆中，统计菜品为菜单上第k道菜的餐桌的数量。m的后验概率符合如下分布：

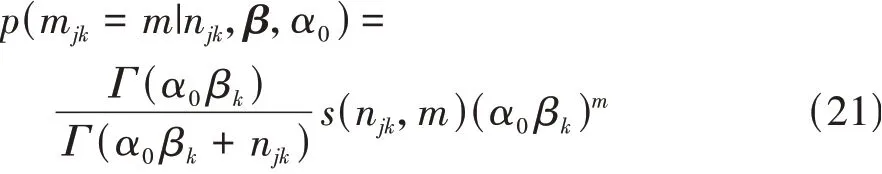
式中s(njk，m)为无符号斯特林数。

zt的后验概率由两部分组成，表示为

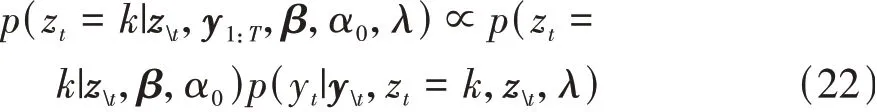
式中：z 表示除时间t以外所有状态；y 表示除时间t以外的所有观测向量。

对于HDP-HMM，第1部分可具体表示为

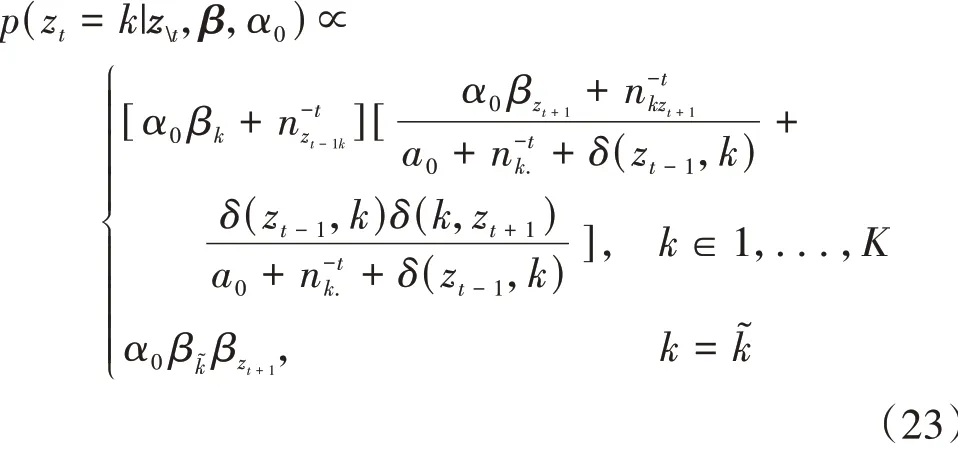
式中：δ(z，k)表示克罗内克δ函数表示从状态k到任意状态的数目，其中不包括原来从zt到zt+1，其它变量含义类似。式（23）表示在t时刻的隐状态概率分布，其中，第1式表示zt属于当前模型已存在的隐状态类型的概率，第2式表示zt属于一个新的隐状态类型的概率。当zt属于当前模型已存在的隐状态类型时，设zt-1=j，zt+1=l，第1式两个中括号［］分别为由隐状态j到隐状态zt的概率g(j)和由隐状态zt到状态l的概率g(l)。

对于DS-HDP-HMM模型，考虑到式（6）定义的解耦黏性过程，从隐状态j到隐状态zt再到隐状态l必须考虑到隐状态自转移概率κ，根据下一时刻隐状态是否保持不变，此过程会产生5种情况：①jjl(l=j)，表示隐状态zt-1到隐状态zt和隐状态zt到隐状态zt+1皆为状态自转移；②jjl，表示隐状态zt-1到隐状态zt为状态自转移，隐状态zt到隐状态zt+1遵循状态转移概率矩阵πzt；③jll，表示隐状态zt-1到隐状态zt遵循状态转移概率矩阵πzt-1，隐状态zt到隐状态zt+1为状态自转移；④jkl，k∈[1，…K]，表示隐状态zt-1到隐状态zt遵循状态转移概率矩阵πzt-1，隐状态zt到隐状态zt+1遵循状态转移概率矩阵πzt；⑤jk͂l，表示隐状态zt为新的状态，zt=k͂。此时式（23）可以改写为

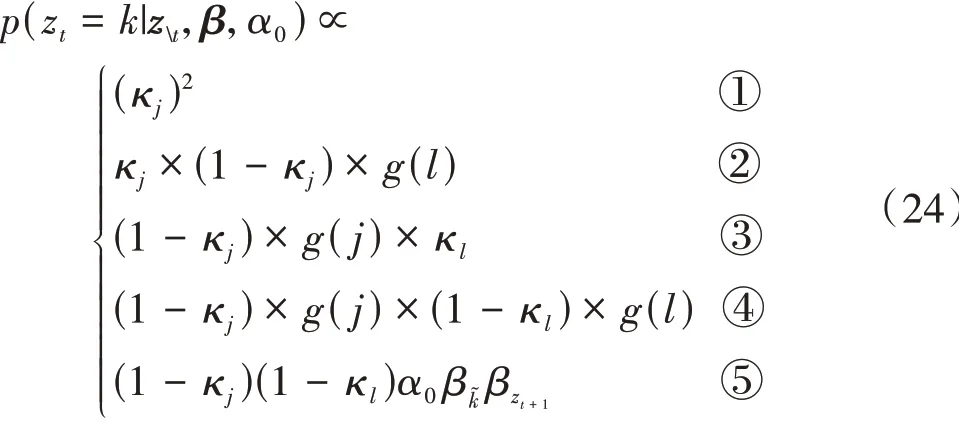
第2部分可具体表示为

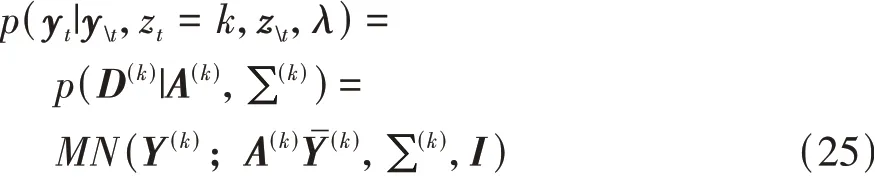
式（25）的实质为1.4节正态-逆威沙特共轭先验的似然函数。其中，I为单位矩阵。

1.5 直接分配Gibbs采样

DS-HDP-HMM采用Gibbs采样算法，基于1.4节CRF模型初始化和参数后验更新规则，经过多轮迭代模型收敛，模型更新流程如表1所示。

表1 基于Gibbs采样的模型更新流程

DS-HDP-HMM模型的超参数先验设置如表2所示。

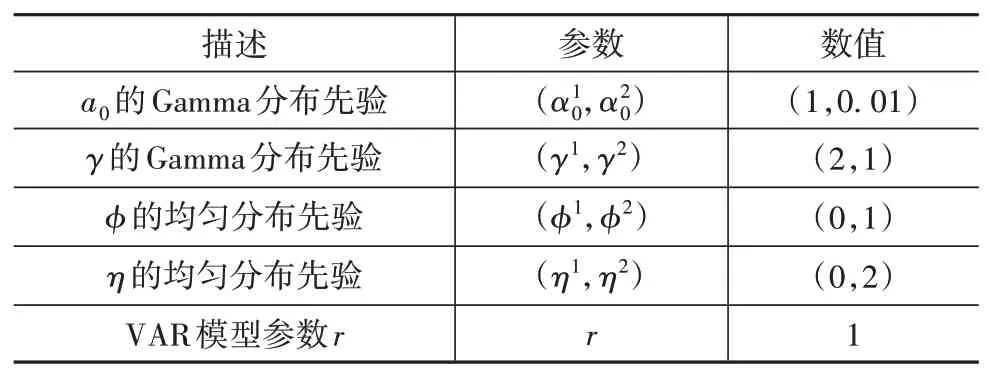
表2 超参数设置

其中，ϕ=ρ1∕(ρ1+ρ2)，η=(ρ1+ρ2)13。

2 测试场景基元提取方法验证

为了验证本文提出的场景基元自动提取方法，选取随机自然驾驶数据库进行场景基元自动提取。

2.1 自然驾驶数据库

本文针对HighD数据集进行场景基元提取测试，HighD数据集提供了来自德国高速公路的自然车辆轨迹数据［20］。HighD数据集使用配备高分辨率摄像头的无人机从空中测量每辆车的位置和运动，在6个不同的位置制作了60条记录，路段的平均长度大约为420 m，每条记录长约17 min（总计16.5 h），其中包含了11万辆车，总行驶距离约4.5万km，含有多种场景工况。

2.2 场景基元提取

基于HighD高速公路数据集，本文将测试场景抽象成图4所示工况。测试场景包括主车所在车道和主车左右两侧车道。主车在纵向自动驾驶算法的控制下在本车道进行加减速运动，只有纵向速度vx一维观测量；每个车道只选取主车前方距离主车最近的至多1辆车，可以按照交通法规自由换道行驶。主车两侧车道的目标车分别有纵向速度vx、相对纵向距离Δdx和相对侧向距离Δdy三维观测量，与主车同车道的前面车辆有纵向速度vx、相对纵向距离Δdx二维观测量。如果对应车道没有车辆，则对应的观测量置0。测试场景多维数据向量输入到模型前，首先要对每一维数据进行［-1，1］标准化，避免不同维度数据范围不同对试验结果产生影响。

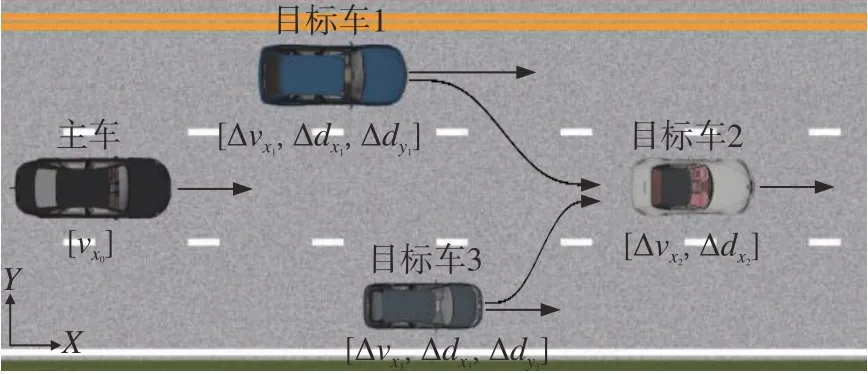
图4 测试场景工况

为了确定模型收敛的迭代次数，本文从HighD数据库随机选择5组测试场景序列作为模型输入，计算其观测向量的对数似然函数，结果如图5所示。可以看出，随着迭代次数增加，5组随机测试场景序列观测向量的对数似然函数结果快速收敛。但是较少的迭代次数可能使输出的场景基元持续时间过短，适当增加迭代次数可以使具有相似特征的场景基元自动合并，使场景基元序列的长度更长，物理含义更加明确。所以，综合考虑计算效率与模型性能，本文最终选择模型迭代次数为100。

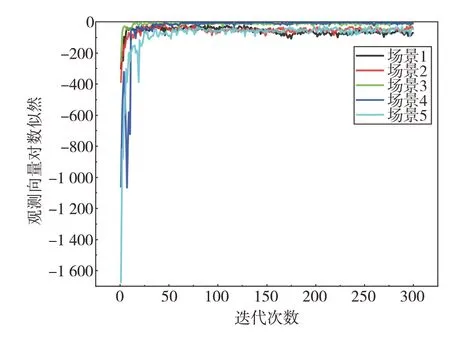
图5 5组随机场景观测向量对数似然

从HighD自然驾驶数据库中随机选取某段测试场景，采用DS-HDP-HMM模型提取场景基元。为了证明采用的模型效果，对比采用基于多维高斯分布作为观测概率分布函数的Sticky HDP-HMM模型提取场景基元，其结果如图6所示，上面9幅图片是测试场景不同维度的观测值输入，下面两幅图片状态序列的不同状态值输出代表了不同类型的场景基元。两种模型在场景基元提取方面存在差异，相比于DS-HDP-HMM，Sticky HDP-HMM场景基元的时间长度更均匀，难以根据车辆的运动特性对场景基元进行不同时长的划分，证明了1.2节中Sticky HDP-HMM模型特征1和特征3不能解耦对场景基元提取造成了影响。并且，由于Sticky HDP-HMM模型采用多维高斯分布作为观测概率分布函数，不能很好地描述车辆的运动。例如在主车纵向速度维度，19.2～22.8和22.8～24.92 s（红色点划线部分）的测试场景分别代表主车加速和主车减速，物理意义上应该为两种类型场景基元，但是在Sticky HDPHMM模型中被分成了隐状态14代表的一种场景基元类型。因为多维高斯分布的边缘分布为高斯分布，这两段场景子序列在主车纵向速度维度均可以用相同参数的高斯分布表示，而高斯分布只能表示主车的速度范围，不能表示速度随时间的变化关系，从而对基元提取结果产生了影响。而本文提出的DS-HDP-HMM模型采用了VAR模型，认为当前时刻的观测值与过去时刻的观测值线性相关，表征了时间属性对观测值的影响，使场景基元提取结果更为精确。

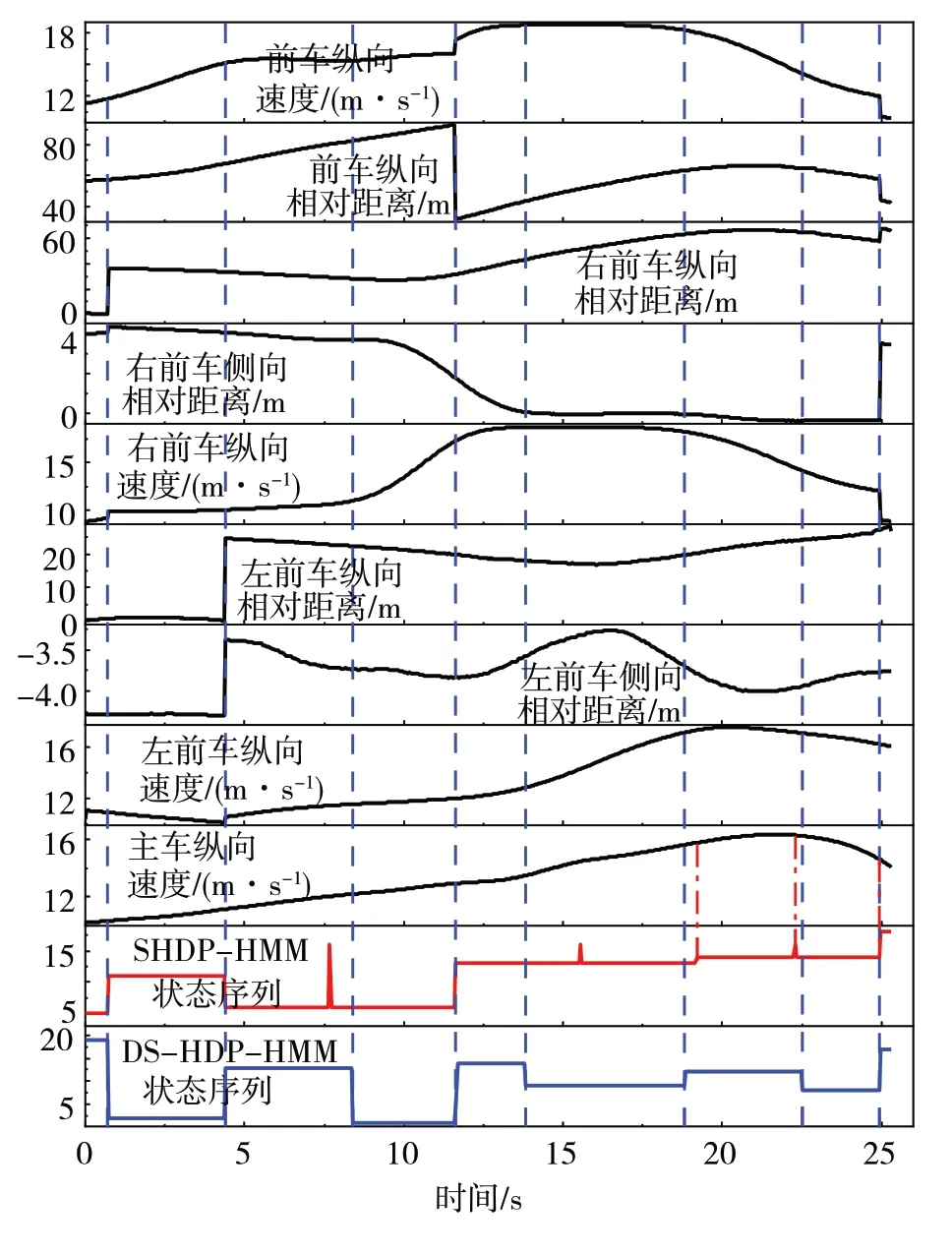
图6 随机测试场景序列基元提取结果

对DS-HDP-HMM模型提取的场景基元的物理含义进行总结，如表3所示，表中的场景基元类别为模型输出的隐状态值。例如，结合图6中的DSHDP-HMM状态序列输出，表中第2行的含义是：模型隐状态为2对应的场景基元时间为0.72～4.36 s，左前车的运动状态为减速未换道，与主车的相对距离近似不变，右前车的运动状态为匀速未换道，与主车的相对距离逐渐减小，前车的运动状态为加速，与主车的相对距离逐渐增大，主车加速。不同类别的场景基元根据主车和周围车辆的运动状态都具有不同的物理含义，具有较强的可解释性。

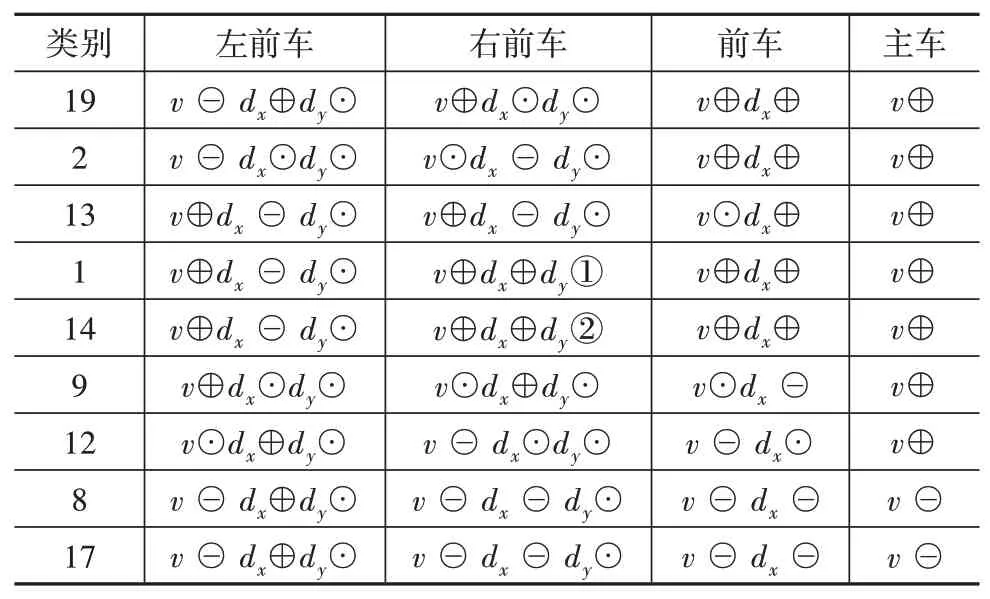
表3 DS-HDP-HMM模型场景基元物理含义

综上所述，本文中采用的基于VAR作为观测概率分布函数的DS-HDP-HMM模型可以在Gibbs迭代过程中通过后验更新自动优化模型参数，从而实现从自然驾驶数据库中非参数地、可解释地、全自动地提取测试场景基元，与Sticky HDP-HMM相比，DS-HDP-HMM提取测试场景基元具有更好的解释性和更高的合理性，具有优良的性能。

3 结论

本文中提出了一种基于自然驾驶数据库的测试场景基元自动提取方法，其结合DS-HDP-HMM模型和VAR模型，将车辆运动状态视为隐马尔科夫过程，采用VAR模型精确拟合车辆运动状态，并加入DS-HDP过程为HMM模型参数提供先验分布和后验更新，最后通过Gibbs采样方法求解HMM模型隐状态，进而实现测试场景基元的非参数、可解释、全自动提取。从HighD自然驾驶数据库中随机选取一段场景序列进行测试验证的结果表明，本文提出的模型可以自动提取自然驾驶数据库场景序列中的场景基元，场景基元具有较强的可解释性。与现有的Sticky HDP-HMM方法相比，本文提出的方法在提取测试场景基元方面具有更高的准确性和合理性。