基于Tube MPC的多轴重型车辆全轮转向路径跟踪策略

王玮琛，李军求，孙逢春，宋 健，吴永华

（北京理工大学，电动车辆国家工程研究中心，北京 100081）

前言

准确有效的路径规划技术推动着智能驾驶车辆进一步提高其路径跟踪效果［1］。路径跟踪的主要目标是合理管理车辆运动，准确跟踪参考路径，保证车辆动态稳定性［2］。

路径跟踪作为一个多目标优化问题，并不是在所有情况下都能获得理想的效果。对于较大的路径曲率或者较低的路面附着系数，路径跟踪精度和车辆稳定性之间会存在冲突。后轮转向（RWS）的方式可增加车辆控制自由度，被证实可以改变和提高路径跟踪过程中的瞬态性能［3-4］。Chen等［5］以零质心侧偏角为目标，通过加入RWS提高极限路径跟踪的综合性能。文献［6］中通过加入后桥差动转向的方式提高八轴重型车辆转向过程的车辆稳定性。除此之外，RWS的加入使两轴车实现了全轮转向。它可以提高两轴车对多余轮胎力的利用，增加安全裕度。文献［7］中证明全轮转向可以实现更大曲率的路径跟踪，可使前后桥轮胎的利用率在必要时最大化，克服了因前轴轮胎力更早达到饱和带来的转向不足问题。同样的，对于多轴车而言，若想充分利用各桥轮胎侧向力，有必要进行全轮转向控制。这样可以使得多轴车辆在大曲率过弯处，各桥可以同时提供更大的侧向力来抵抗车辆所受的离心力［8］。但是，如果对每个桥进行单独控制，其控制成本是昂贵的。

在路径跟踪算法方面，MPC是目前使用的最广泛的方法，因为它可以预测系统未来状态，实现多目标优化［9］。但是，针对求解过程存在不确定性干扰，如轮胎参数不确定以及侧向风干扰等影响，普通MPC的优化效果会大打折扣。为了解决这一类问题，有越来越多的关于Tube MPC的车辆控制算法被提出。Tube MPC将无不确定性系统（标称系统）约束在容许区域内［10］，可以实现鲁棒正不变集的离线计算，策略在线计算量相对小。Mata等［11］提出了基于mRPI的Tube MPC解决了路径跟踪过程速度不确定性干扰的问题；Gao等［12］针对无人车避障问题，提出了基于鲁棒可达集的非线性MPC解决方案。但是现有的关于Tube MPC的研究中，无论是鲁棒正不变集还是可达集的求解，都是基于Minkowski求和进行迭代计算，所求得的集合的顶点数会随着迭代次数的增加呈指数增长。这极大增加集合离线计算的负担，复杂的集合也会降低MPC在线求解的效率。

针对以上所提及的全轮转向策略及控制算法的问题，本文中以五轴重型车辆为研究对象，提出了一种基于Tube MPC的全轮转向路径跟踪策略。首先为了改善多轴车辆在路径跟踪过程中的灵活性和提高各桥轮胎的利用率，提出了基于前桥（第1桥）和后桥（第5桥）转角控制的全轮转向路径跟踪策略。所提全轮转向策略仅有两个控制自由度，同时其控制可使前两桥和后三桥在转向过程分别实现侧偏角响应同步。该策略可以视为两轴车中AFS叠加DWS的延伸。其次，在面对路径跟踪过程中轮胎参数不确定以及侧向风干扰的问题，通过采用Tube MPC的策略来提高路径跟踪控制的鲁棒性。针对mRPI在迭代计算中计算量大及顶点数多的缺点，应用了一种基于支撑函数理论的高效mRPI求解方法取代原有的基于Minkowski求和的方法。最后，通过半实物仿真验证了所提全轮转向策略相对其他全轮转向策略在路径跟踪效果上的优势，同时验证了Tube MPC策略在面对干扰的情况下对比常规MPC策略有更好的鲁棒性。基于Tube MPC的全轮转向路径跟踪策略的整体控制框架如图1所示。

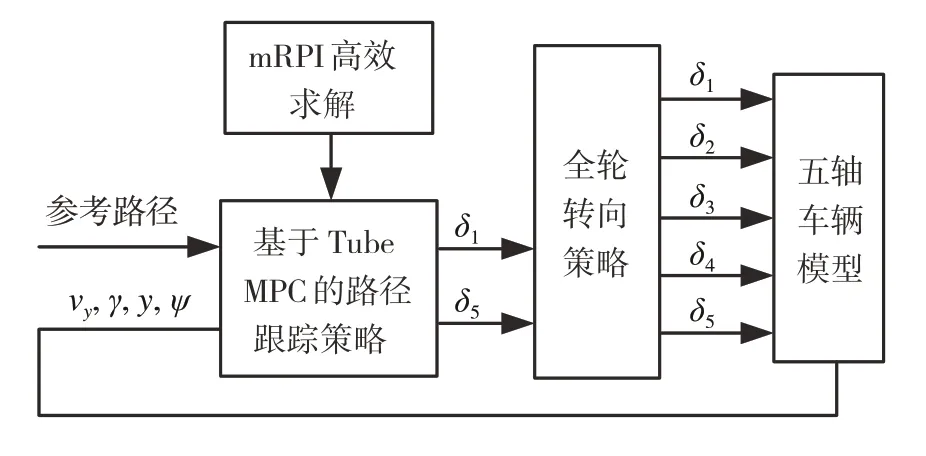
图1 控制框图

1 整车动力学建模

本节基于某五轴重型车辆，建立18自由度的非线性整车动力学模型，包括车身纵向、横向、横摆运动3个自由度、5个转向自由度和10个车轮旋转自由度。

1.1 车身纵向-侧向-横摆3自由度模型

图2为五轴重型车辆的动力学分析图。

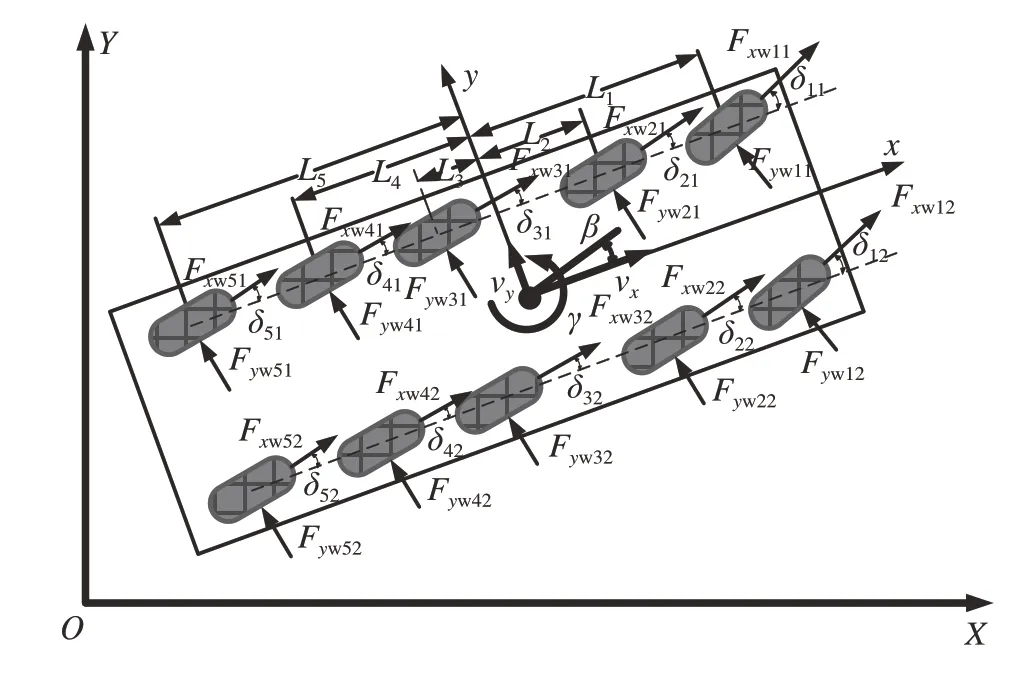
图2 五轴重型车辆动力学分析图

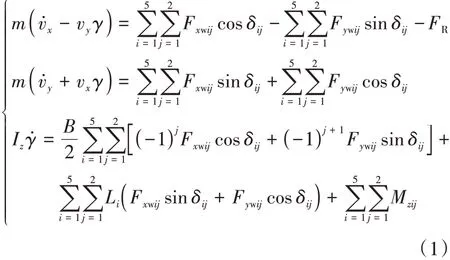
车身纵向、侧向及横摆运动关系式可表示为式中：i∈{1，...，5}代表第i轴，j∈{1，2}代表左右侧车轮；m、vx、vy和γ分别为整车质量、车辆纵向速度、车辆侧向速度和车辆横摆角速度；Fxwij、Fywij和Mzij分别为轮胎受到的纵向力、侧向力和回正力矩；δij为对应轮胎转角；FR为行驶阻力；Iz为车辆绕z轴的转动惯量；B为车辆的轮距；Li代表各轴到质心（CG）的水平投影距离，在质心前方为正，后方为负。

1.2 轮胎载荷计算

如图3所示，本文的研究对象装备有多轴互联式油气弹簧悬架，与其相连通的同侧悬架的输出力情况相同［13-14］。

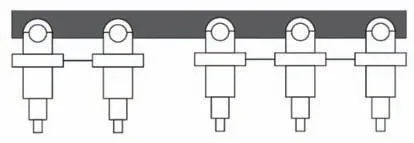
图3 多轴平衡式油气弹簧系统示意图

在获取各轴轮胎静态载荷时，可将车辆视为两轮自行车模型进行计算，前两轴的静态垂向力相等，后三轴的静态垂向力相等。加上考虑纵横向加速度，各轴垂向力表示如下：

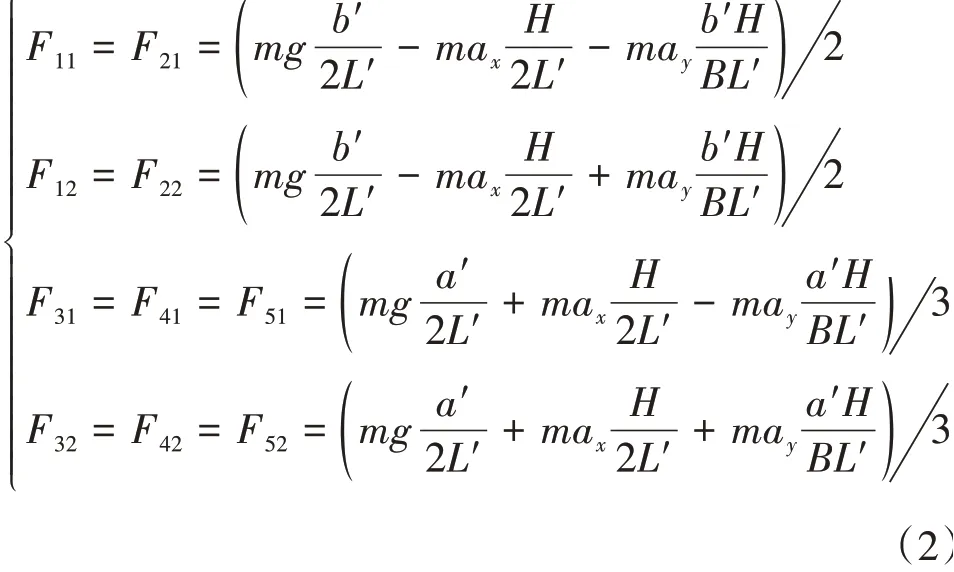
式中：H为质心高度；ax和ay分别为纵向和横向加速度；a'和b'分别代表等效前后轴距，满足：

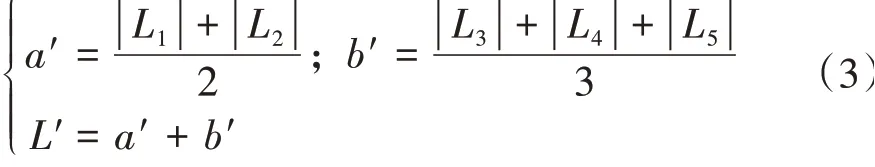
1.3 车轮运动模型

以单个车轮为例，其旋转运动的微分方程可表达为

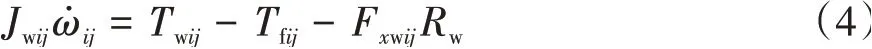
式中：Jwij为车轮的转动惯量；ωij为车轮角速度；Rw为轮胎滚动半径；Twij为轮毂电机施加给车轮的驱动∕制动转矩；Tfij为地面产生的滚动阻力矩。

各车轮中心的纵向和侧向速度可表示为

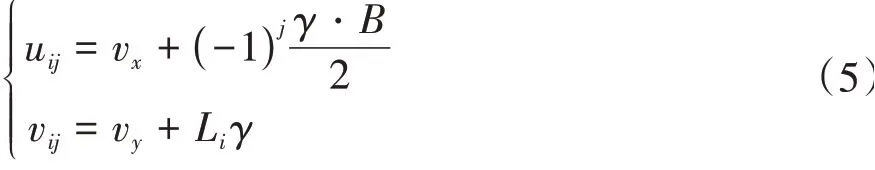
车轮在对应轮胎坐标系下的速度为

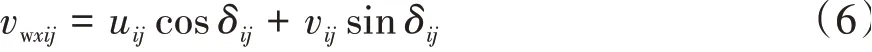
最终可获得车轮的滑移率和侧偏角：

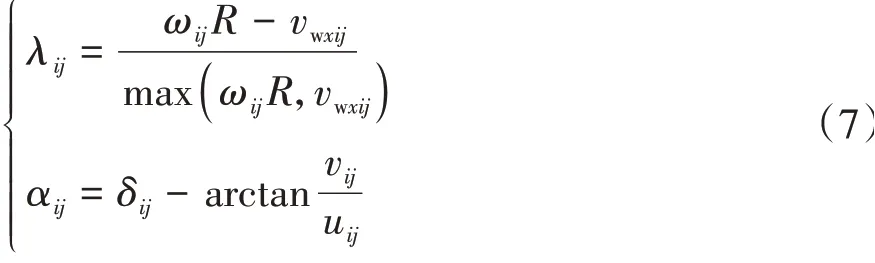
1.4 轮胎模型

基于Pacejka教授提出的“Pacejka2002”版本的魔术公式模型建立轮胎模型。联合工况下的轮胎力可以表示为

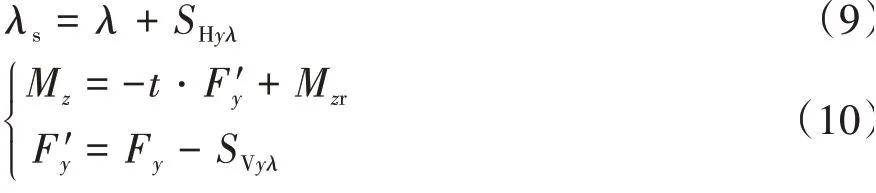
式中：Fx、Fy和Mz为联合工况下轮胎所受的纵向力、侧向力和回正力矩；Fx0和Fy0分别为纯纵滑的纵向力和纯侧偏的侧向力；Gxα和Gyλ为联合工况下对纵向力和侧向力的加权函数；Cxα和Cyλ为形状因子；Bxα和Byλ为刚度因子；Exα和Eyλ为曲率因子；SHxα、SHyλ和SVyλ为曲线水平漂移；t为轮胎拖距；Mzr为残余力矩。

2 控制模型搭建

控制模型的搭建基于所提出的全轮转向策略，在五轴车辆的线性2自由度模型基础上考虑了路径跟踪过程轮胎参数不确定性和强侧风产生的有界干扰。

2.1 全轮转向策略制定

对于多轴车辆路径跟踪，不考虑急加∕减速情况，根据前面分析，单轨模型的前两桥静态垂向载荷相等，后三桥也相等。近似匀速的路径跟踪工况下各轮滑移率很小，纯侧偏轮胎模型能有效且准确逼近联合工况轮胎模型的结果，因此前两桥和后三桥的侧向力特性相近。基于此，本文中提出前后转角控制的全轮转向路径跟踪策略，控制量只有两个，为u=[δf，δr]。其 中δf以 第1桥 的 转 向 角 为 基 准，δf=δ1，δr以第5桥的转向角为基准，δr=δ5。各轴转角和控制量存在如下关系：

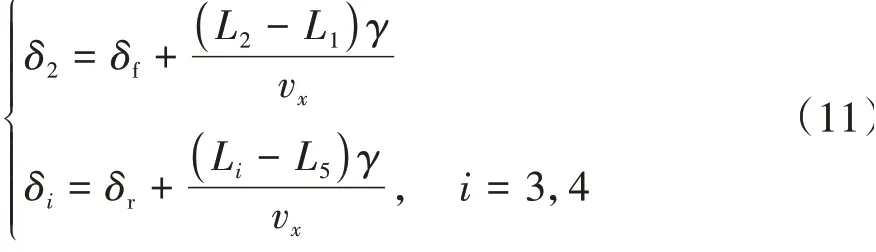
该转角关系可以保证前两桥和后三桥轮胎侧偏角分别实现同步。当第1桥和第5桥轮胎侧向力获得最大化利用的同时，中间桥轮胎的利用率可以实现同步。这避免了多轴车辆某些桥侧向力达到饱和时，其他桥侧向力利用率仍然很低的情况，有利于提高车辆在大曲率过弯时的路径跟踪性能［8］。

2.2 控制模型建立

图4为线性2自由度模型示意图。

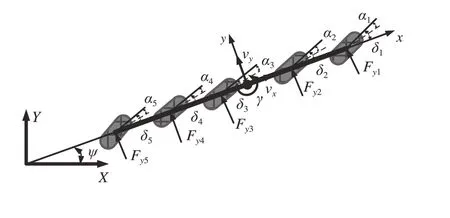
图4 线性2自由度模型示意图

控制模型为考虑五轴车辆的线性2自由度动力学模型：

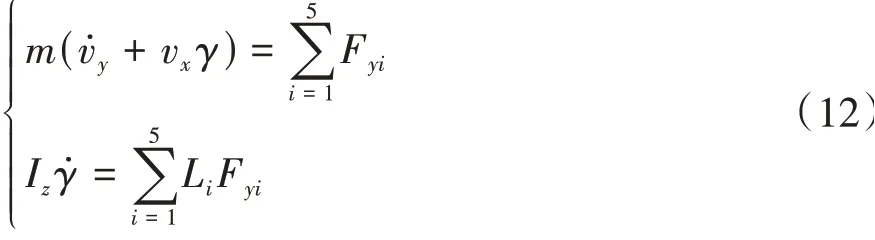
式中Fyi为各桥侧向力。侧向力和侧偏角的关系为

其中，记前两桥侧偏刚度为Cf，后三桥侧偏刚度为Cr。

以第1桥和第5桥转向角为控制变量，各桥的轮胎侧偏角可以表示为

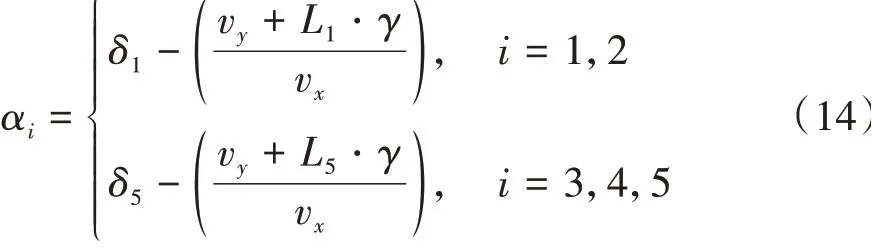
车辆的横向距离y和车辆航向角ψ的关系式如下：

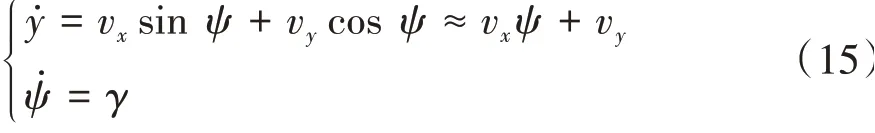
整理式（12）～式（15），得到状态空间方程：

将式（16）通过零阶保持的方式进行离散化：

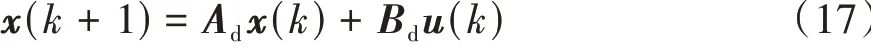
控制模型参数基于固定的纵向车速vx，同时考虑的轮胎侧偏刚度Cf和Cr是在道路附着系数为μ0时对应的值。考虑有界干扰w(k)包括两部分，即轮胎参数不确定性和环境中侧向风的扰动。实际被控系统表示为

x(k+1)=Adx(k)+Bdu(k)+w(k) （18）

轮胎参数的干扰实际由两部分引起。首先标称系统中忽略了轮胎的非线性特性；其次是当路面附着变化μ≠μ0时，实际的轮胎侧偏刚度和标称系统对应的侧偏刚度不匹配。同时强侧向风的突然出现，会使得车辆所受到的侧向力和横摆转矩发生突变，影响路径跟踪性能。对于多轴车而言，其较大的外形尺寸对应大的迎风面积会加剧侧向风的影响。

3 基于Tube MPC的路径跟踪策略设计

Tube MPC控制算法是将标称系统从实际系统中分离出来，通过计算mRPI将标称系统状态量和控制量约束在新的范围内，从而有效维持控制系统的稳定性。

3.1 Tube MPC理论

式（18）实际系统，其状态量x(k)∈R4，控制量u(k)∈R2，有界干扰量w(k)∈R4。同时，系统受到的约束为x(k)∈X，u(k)∈U，w(k)∈W。X、U和W为包含内点的多面体集合（紧凸集）。分离有界干扰对系统的影响，定义如下标称系统：

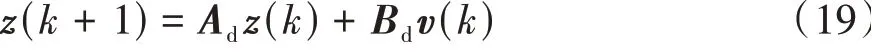
式中：z(k)∈R4为标称系统状态；v(k)∈R2为标称系统控制量。

则实际系统和标称系统的状态量误差为

控制目标须在不违反约束的情况下，补偿实际状态和标称系统状态之间的误差，使得标称系统状态尽可能接近参考。由此，定义实际系统的控制输入为

式中K为状态反馈增益，通过极点配置进行离线选择，可以保证Acl=Ad+BdK严格稳定。

联立式（18）～式（21），可以求得误差系统的闭环状态方程：

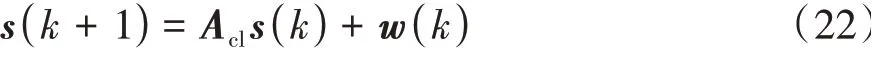
定义S为误差系统的鲁棒正不变集（RPI），也称为Tube。对于任意的有界扰动，当误差状态位于RPI之内，其状态演化一定还在RPI之内：

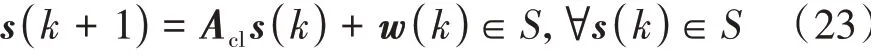
用集合的形式可以表示为

式中⊕表示集合之间的Minkowski和运算，对于给定两个集合M，N⊂Rn，Minkowski和定义为

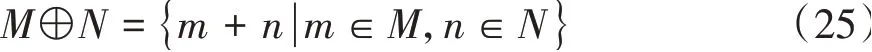
由此可获得标称系统的状态量和控制量的约束为

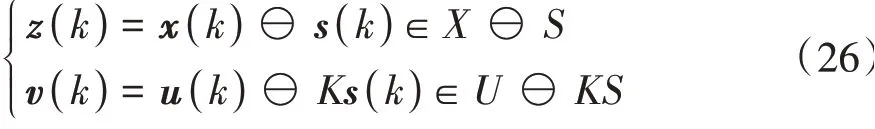
式中⊖为集之间的Pontryagin差运算。对于给定两个集合M，N⊂Rn，Pontryagin差定义为

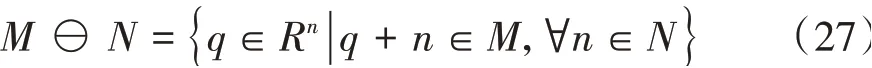
3.2 mRPI的高效计算

更小的RPI会形成较小的约束收紧，同时也会使系统获得更好的鲁棒性和较低的保守性［15］。mRPI包含在所有RPI中。mRPI通过如下序列的极限集获取：

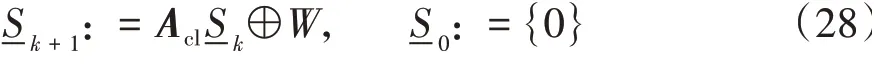
mRPI满足Smin=-S∞。虽然-S∞不是有限确定，文献［16］中提出有限次迭代的方法外近似以获取mRPI，其目标是寻找到数组(k*，ε)使其满足：

则最小鲁棒不变集为

因此，本研究通过采用一种高效的mRPI计算方法［17］来替代基于Minkowski求和的传统求解方法。

首先定义集合X、U和D分别为

则最大鲁棒不变集（MRPI）同样可以通过序列的极限集给出：

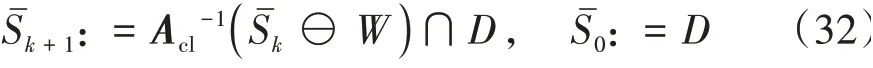
mRPI、MRPI等相关集合满足如下关系：

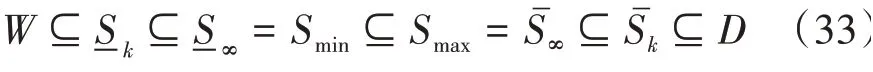
相关MRPI可以借助支撑函数的概念进行计算，同时集合的顶点数量只会随着迭代次数呈线性增加。但是，Smax通常比Smin大的多。据此，文献［17］中重新构造了一个集合满足：

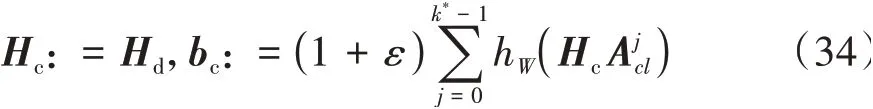
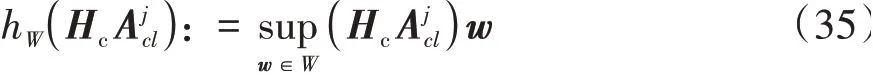
因此可以通过式（36）的迭代求解集合P∞。

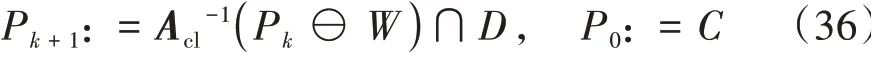
P∞逼近mRPI，同时也保证了式（37）的成立。

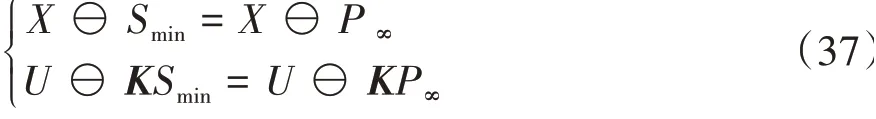
对于P∞的求解可以通过k次迭代实现，其中k≤并 且满足：

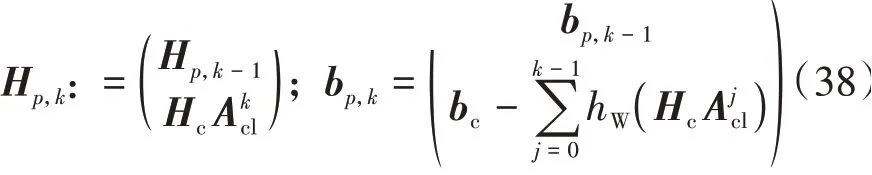
高效mRPI的具体计算流程如表1所示。

表1 高效mRPI计算流程

3.3 基于Tube MPC的求解问题构建

MPC作为一种最优控制方法，求解器从系统状态反馈中推导出未来状态，并根据给定的参考输出，通过最小化性能指标确定最优控制序列。然后将控制序列中的第一个元素作为当前时刻的系统控制量。mRPI（Smin）的求解用于对MPC优化问题中约束的重新制定。实际系统和标称系统在初始点的误差应保证在Smin内，才能满足MPC迭代的可行性。同时，Smin收紧迭代过程状态量和控制量约束，保证策略的鲁棒性。具体关于五轴车辆路径跟踪的Tube MPC的优化问题构建如下：

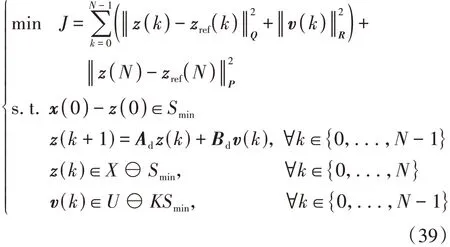
其 中z(k)∈X⊖Smin等 价 于因此z(k)和v(k)约束收缩均可通过支撑函数计算。

式中：N为预测步长；Q、R和P分别为状态量、控制量和终端代价权重矩阵；zref=[vy，refγrefyrefψref]T为标称系统的参考状态，在Q中仅对侧向速度、横向距离和航向角的跟踪误差施加惩罚，以保证车辆稳定性和路径跟踪精度。

对应地，取侧向速度参考量vy，ref(k)=0。对于横向距离参考量yref(k)和航向角参考量ψref(k)的获取，首先根据车辆当前时刻的位置，获取在参考路径上距离其最近的点[xref(0)，yref(0)，ψref(0)]。并以此为起点获取预测视界对应的参考路径预览点序列[xref(k)，yref(k)，ψref(k)]，其中 相邻 两 点满 足关系：xref(k+1)-xref(k)=vx·T。

经式（39）优化求解可以获得标称系统的控制量v*(0)和对应标称系统初始状态量z(0)，则实际系统最终的控制量为

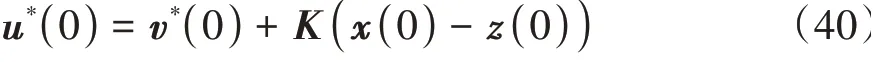
式中x(0)为实际系统反馈的当前时刻的状态。

定义实际状态量x和实际控制量u的约束如下：

如2.2节所述，模型扰动考虑了线性轮胎模型的不确定性、附着不确定性和侧风扰动。标称模型中附着系数为μ0=0.8，考虑实际道路附着系数μ∈[0.4，1]，侧向风速v∈[0，25]m∕s。获取标称系统和实际系统在采样时间T=0.1 s的一步状态预测偏差（扰动）范围为

关于mRPI的计算，取ε=0.01，对应的k*=19，表明传统的Minkowski求和运算需要经过19次迭代计算，而当进行到第5次迭代时，不变集的顶点数就多达2 116个。对于本文所采用的高效mRPI算法，最终结果仅有78个顶点。由于最终的简化mRPI为四维多面体，通过命令“projection”将其进行三维方向投影，如图5所示。

图5 简化mRPI三维投影图

4 硬件在环仿真验证

结合所提策略模型和整车动力学模型搭建了硬件在环仿真平台，以验证所提策略的有效性和实时性。仿真流程和平台如图6和图7所示。将整车动力学模型下载到Speedgoat实时仿真机中，控制策略下载到整车控制器（VCU）中。VCU和实时仿真机通过CAN总线实现信息交互。基于Tube MPC策略的主要仿真参数如表2所示。

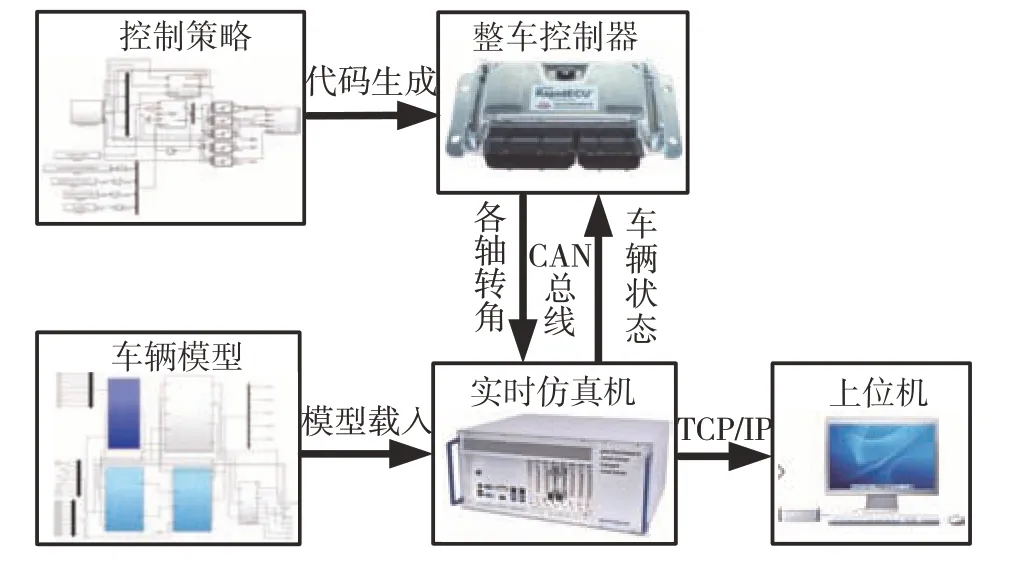
图6 硬件在环仿真流程

图7 硬件在环仿真平台

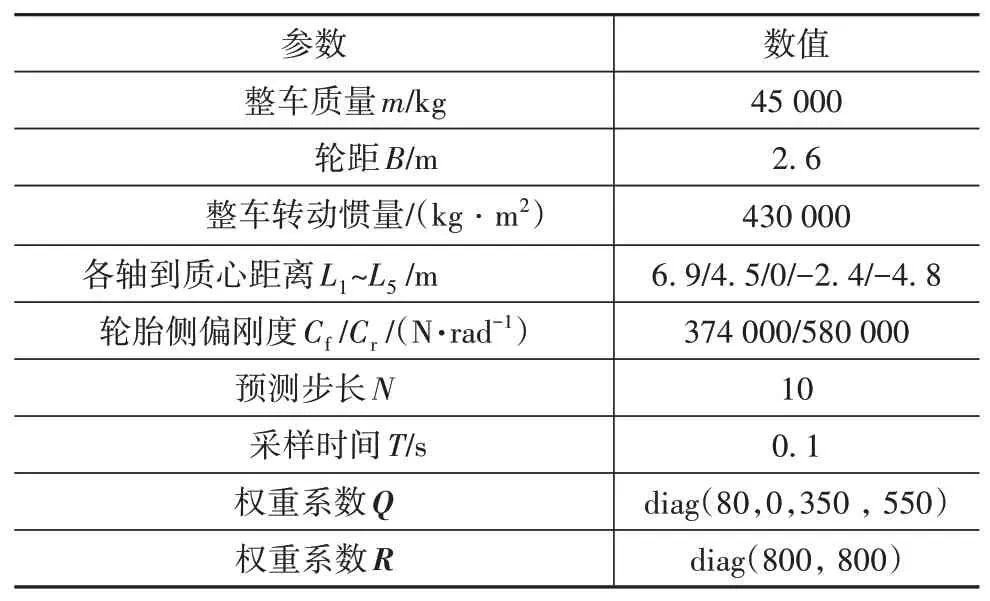
表2 主要仿真参数

除了所描述的Tube MPC横向路径跟踪策略之外，同时设计了基于PID的纵向控制器保证路径跟踪过程的匀速条件，车辆所需的纵向力矩T(k)可以表示为

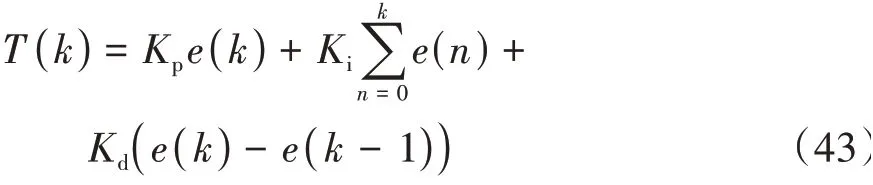
式中：Kp、Ki和Kd分别为比例系数、微分系数和积分系数；跟踪误差为e(k)=vx_ref-vx，vx_ref为目标纵向车速。

仿真包括3个内容。仿真1首先对所提全轮转向策略进行验证，并将其与另外两种全轮转向策略进行对比，对于3种策略的求解均采用基于线性2自由度模型的普通MPC，不涉及Tube MPC求解策略。对比策略1为基于阿克曼原理的全轮转向策略，只有一个控制自由度。转向中心在车辆几何中心的延长线上。对比策略2根据文献［6］设置，基于第1桥和第5桥转角进行控制，第1、2桥和第3、4、5桥分别共享转向自由度，且它们的转向中心均在车辆纵向几何中心的延长线上，但不重合。两个对比策略的转角关系示意图如图8所示，两个对比策略的转角关系分别如式（44）和式（45）所示，li为各桥到纵向几何中心的距离。

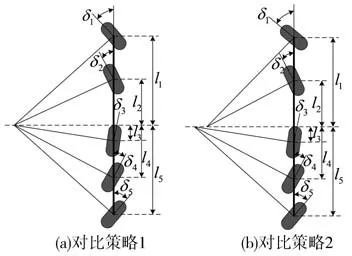
图8 两种对比策略的转角关系示意图

仿真2和3，基于相同的全轮转向策略，对所提出的Tube MPC路径跟踪策略和普通MPC策略进行对比验证。虽然仿真2和3中受到的扰动不同，但它们均属于有界扰动，满足式（42），3.3节求得的mRPI对它们都是适用的。

4.1 全轮转向策略验证

仿真工况1选取路面摩擦因数为μ=0.8，目标参考路径设置如图9所示，为蛇行工况，被控车辆的纵向目标车速为25 m∕s。

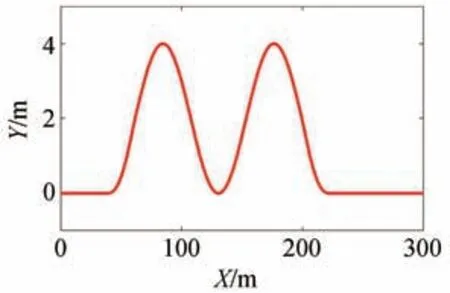
图9 参考路径

图10为所提全轮转向策略以及对比策略的转角求解结果。可以看出，所提全轮转向策略和对比策略2前后桥通过同向转向实现路径跟踪，而对比策略1的阿克曼转向前两桥和后三桥转向方向相反。图11为各桥轮胎侧偏角，图12为路径跟踪效果对比图，结合图11和图12可以看出，阿克曼转向策略早早失去了对路径的跟踪控制。当然，这也说明了增加转向控制自由度有助于提高车辆的控制效果。以下的结果分析中对于对比策略1的结果不再赘述。

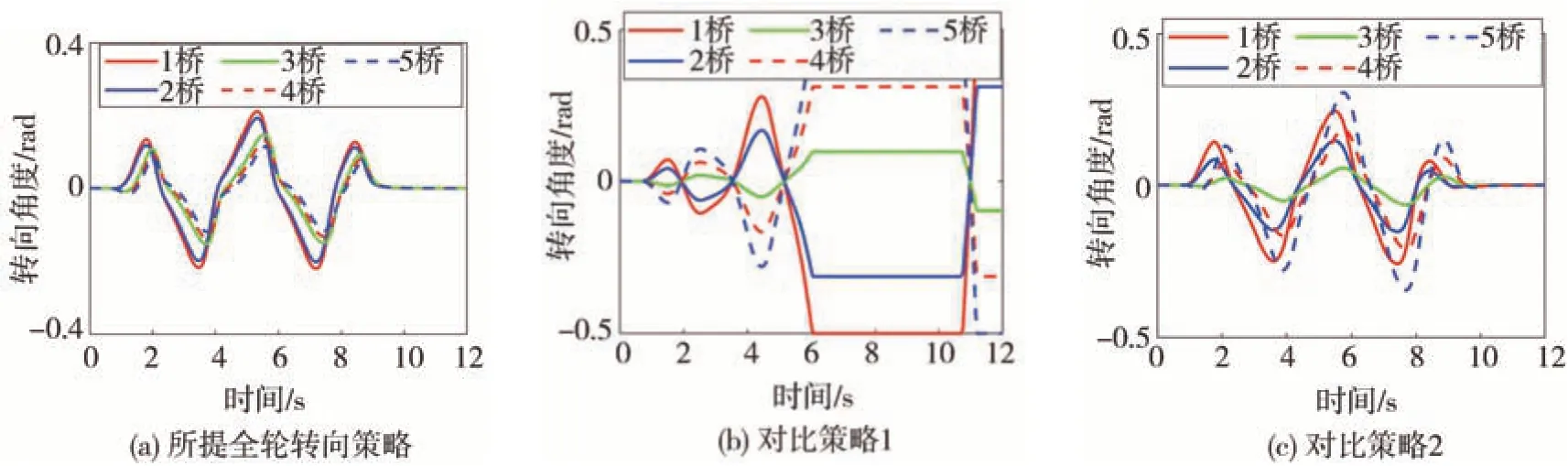
图10 转角结果图

通过图11不同策略之间各桥轮胎侧偏角的对比中可以看出，在路径跟踪过程中所提全轮转向策略可以分别实现前两桥和后三桥轮胎质心侧偏角的同步；而对比策略2中第2桥和第3、4桥侧偏角的响应分别滞后于第1桥和第5桥，同时也难以通过调节第1桥和第5桥的转角使得其他中间桥的轮胎侧向力充分发挥。如图11（c）中，在t=6 s和t=8 s时，第5桥的侧偏角达到0.4 rad，到达轮胎侧向力饱和区，而此时第3桥的侧偏角只有0.1 rad，侧向力还有较大的利用空间。相反的，所提的全轮转向策略则可以及时给整车提供足够的侧向力缓解过弯时的转向不足，侧向力的贡献对于前两桥和后三桥而言是平均的，它们无须使第5桥轮胎逼近或者超过饱和区。

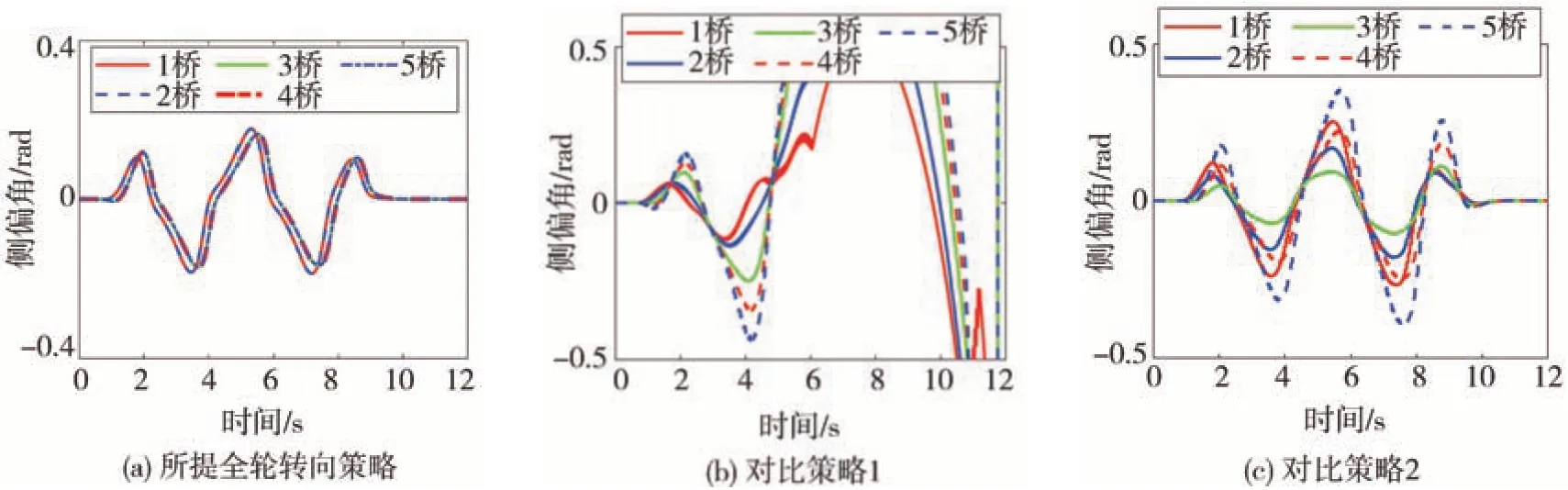
图11 各桥轮胎侧偏角

因此，图12（a）中所提全轮转向策略对应的侧向速度相较于对比策略2更小，最大值不超过0.5 m∕s，车辆拥有更高的稳定性。由图12（b）可见，所提策略的横摆角速度同时也更为平滑。图12（c）和图12（d）显示了所提全轮转向策略在横向位移误差和航向角误差的控制方面优于对比策略2，横向位移偏差的最大值只有对比策略2的40%，所提全轮转向策略拥有更高的路径跟踪精度。

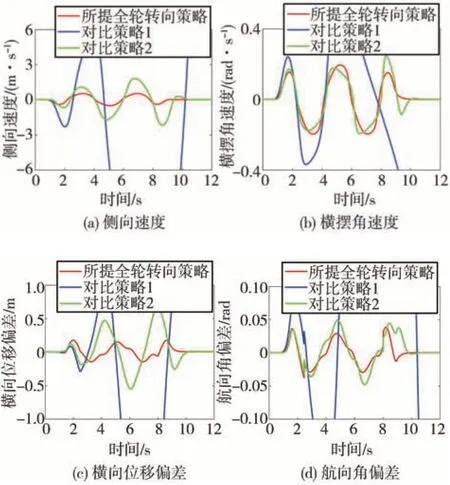
图12 路径跟踪效果对比

4.2 轮胎参数不确定工况

仿真工况2参考路径设置为如图13（a）所示的双变道工况，对应的实际路面附着系数如图13（b）所示，车辆纵向目标车速为25 m∕s。标称模型中的线性轮胎模型对应在路面附着系数μ0=0.8时获得。如在第2节中所提到的，轮胎参数的不确定性可以包括线性轮胎模型带来的不确定性和路面附着不确定性。参考路径中对应的两次变道试验，是对这两个不确定性的分别验证。由于对应在第一个变道参考路径转弯处曲率较大，单纯通过线性区域轮胎力不足以完成路径跟踪。而Tube MPC策略考虑了轮胎非线性部分造成的扰动，如图14所示，其求解获得的转角结果也不像普通MPC策略的转角变化那么剧烈，对应的转角峰值更小。如图15所示，普通MPC对应的轮胎侧偏角甚至都到达饱和区域附近，而Tube MPC对应的侧偏角则小得多。

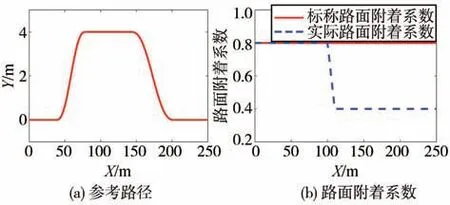
图13 仿真工况设置

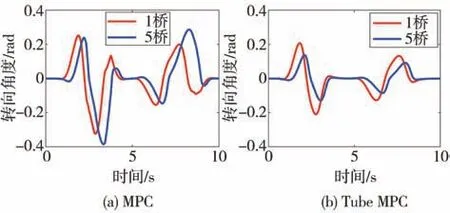
图14 转角结果图

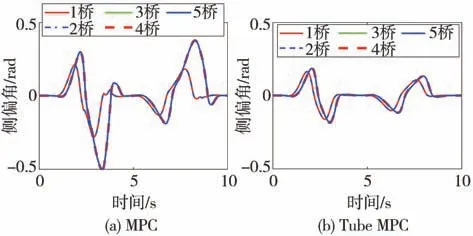
图15 各桥轮胎侧偏角

图16为路径跟踪效果对比。由图可见，对于轮胎非线性区域的适配导致在t=3.5 s附近，MPC策略产生一个较大的侧向速度，为2 m∕s。对应的横向位移误差峰值接近0.5 m，航向角误差峰值接近-0.1 rad。而基于Tube MPC的路径跟踪策略可以将侧向速度维持在一个较小的范围，即0.5 m∕s之内；对应的横摆角速度变化也较符合路径曲率变化的趋势，变化缓和。对应的第2个变道过程，道路实际附着系数为0.4，Tube MPC策略同样展现出在抑制模型不确定性方面的优势。整个路径跟踪过程，Tube MPC策略将横向位移偏差均方根值由0.135 4减少到0.064 6 m，减小了52.3%。综上，表明了Tube MPC对比普通MPC在面对轮胎参数不确定时，可以表现出更好的路径跟踪性能。

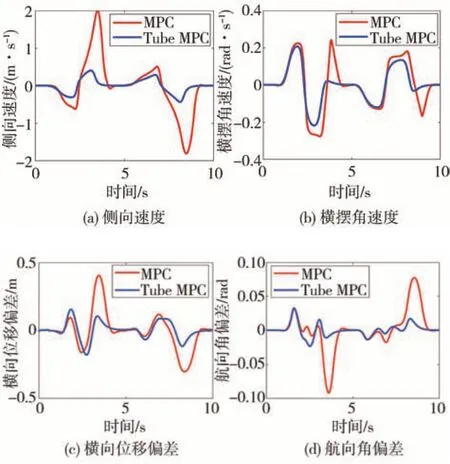
图16 路径跟踪效果对比

4.3 轮胎参数不确定叠加侧向风干扰工况

仿真工况3在附着系数为0.5的路面上进行，仿真工况设置如图17所示。在1～4 s，有风速为25 m∕s的脉冲式侧向风由车辆右侧吹向车辆左侧。经计算，在此期间侧向风对车辆产生的附加侧向力和横摆力矩分别为Fyw=23026 N和Mzw=30748 N·m。图18为路径跟踪过程的转角求解结果，普通MPC策略对应的转角波动大，峰值也大；而Tube MPC策略对应转角则平缓得多。图19为路径跟踪效果对比。由图可见，类似于仿真2，Tube MPC策略在面对轮胎参数不确定性和侧向风的外界干扰下，展现出优于普通MPC策略的动力学稳定性。特别地，由于横摆力矩的影响，MPC策略在第2个转弯t=3.5 s处，横向位移出现一个向左侧的超调，横向位移偏差最大到达0.7 m。而Tube MPC控制器在路径跟踪过程横向位移偏差最大值仅为0.32 m，减小了54.3%，横向位移的均方根误差值从0.292 7减少到0.121 7 m，减小了58.4%。这同样说明Tube MPC策略有更强的抗干扰能力。

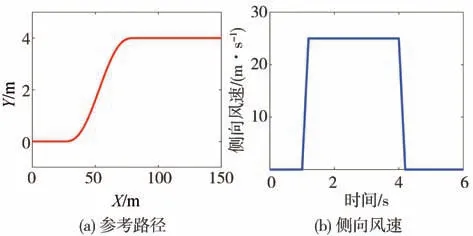
图17 仿真工况设置

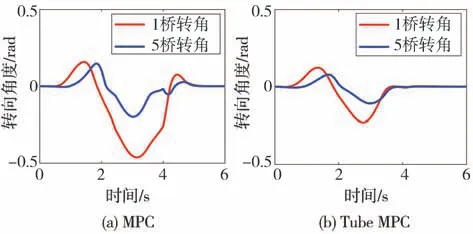
图18 转角结果图

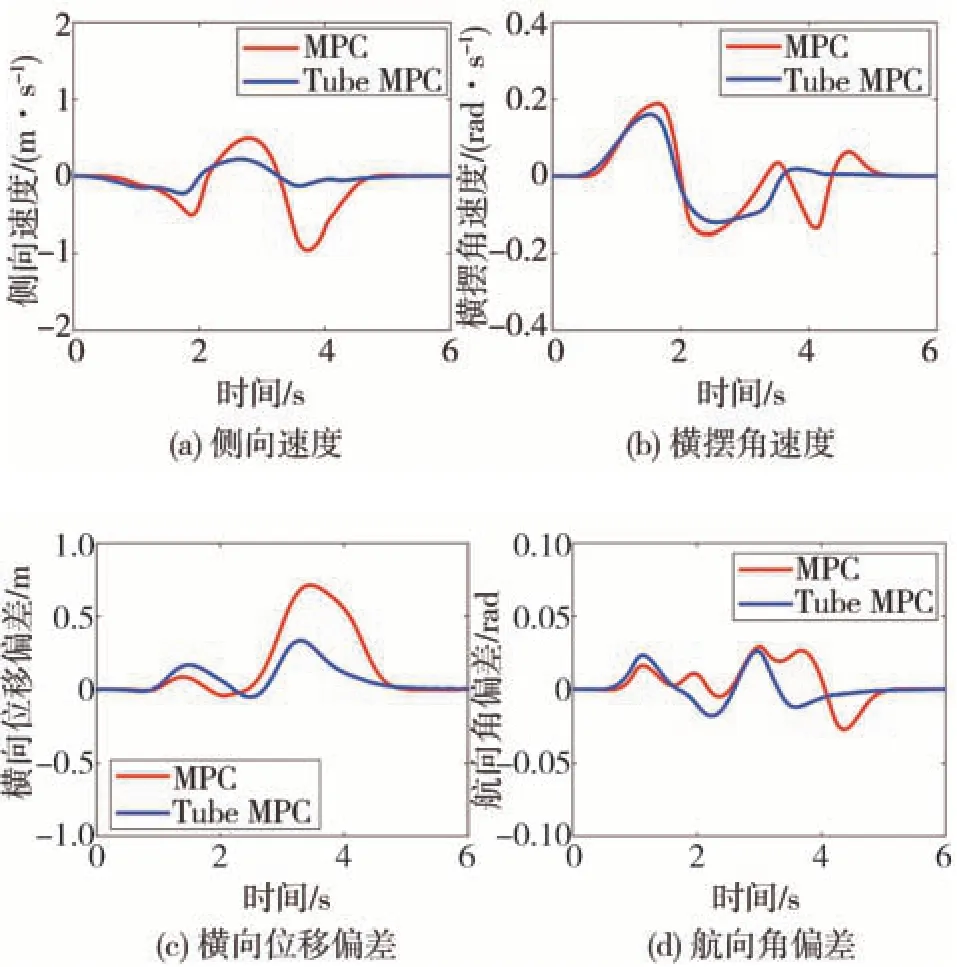
图19 路径跟踪效果对比

5 结论

本文以五轴重型车辆为研究对象，提出了基于Tube MPC控制的全轮转向路径跟踪策略，得到如下结论。

（1）设计基于第1桥和第5桥转角控制的全轮转向路径跟踪策略，使得多轴车在路径跟踪控制上更灵活且各桥侧偏角可实现同步，同时各桥侧向力有机会获得充分利用。

（2）考虑轮胎参数不确定性和侧向风干扰的控制模型，运用Tube MPC策略进行路径跟踪问题求解。

（3）采用基于支撑函数的高效mRPI算法代替Minkowski和运算的迭代方法，有效减少了不变集的顶点数，可以提高离线不变集计算和在线策略运算的效率。

（4）通过半实物仿真验证表明，所提出的全轮转向策略对比普通的全轮转向策略有更好的路径跟踪性能，同时证明基于Tube MPC的全轮转向策略面对未知干扰，有更强的鲁棒性，可以获得较高的跟踪精度和车辆稳定性。