增压条件下浮沉子不可逆下沉的动力学研究

欧阳严严，陈 靖，陈宗强，孔勇发

(南开大学 物理科学学院，天津 300071)

浮沉子由法国科学家笛卡尔发明，为玻璃制的小瓶体，其下端开有小孔，水可通过小孔进出瓶体. 把浮沉子放入高贮水筒中，并使之浮在水面上. 用薄橡皮膜覆盖筒口并扎紧，用手按橡皮膜，筒内的水和空气在密闭的容器内. 可以通过调节外加压强的大小，改变浮沉子的排水体积来实现浮沉子的浮沉. 根据帕斯卡定律，当改变外部封闭容器中的压强时，试管内的水会被排出或试管外部容器中的水会被挤入，导致空气柱的体积增大或者减小，从而改变浮沉子受到的浮力，实现上浮或者下沉.

浮沉子在液体中特定位置的浮沉状态受到其几何结构[1]、外界压强[1]、液体密度[1-2]以及温度[3]等因素的影响. 由于浮沉子在展示浮力变化以及浮力与重力的相对大小方面具有现象明显的特点，故常常作为教具[4-6]. 浮沉子原理也被应用于高空气球形貌的预测[7]、磁力浮沉子密度计的设计[8]、检测高浓度水[9-10]等. 由于浮沉子的研究内容广泛而有趣，该内容被选为2021年IYPT的第6题：不可逆转浮沉子.

本文首先通过受力分析给出了浮沉子发生不可逆下沉的原因是由于浮沉子所受浮力小于增加的压强给浮沉子向下的力. 接着，从势能角度给出了在增压情况下浮沉子的临界深度位置，解释了浮沉子不可逆下沉点的物理本质为不稳定平衡的势能极大值点，并讨论了压强的改变对该势能极大值点存在性的影响. 最后，通过实验验证了浮沉子不可逆下沉点的位置，并探究了相关参量对不可逆点位置的影响.

1 理论分析

1.1 浮沉子不可逆临界深度的分析

假设气体均为理想气体，且浮沉子内气柱温度以及水温保持恒定不变.记浮沉子下降到一定深度时顶端到液面的距离为x，气柱位于液面下的部分高度为ξ，浮沉子的不同状态如图1所示.

(a)与液面齐平 (b)液面上方 (c)液面下方

对浮沉子中的气柱，由玻意尔方程可得：

(1)

其中，p0为大气压强，l0为未放入水前浮沉子初始气柱的长度，ρ为液体的密度，g为重力加速度，p为液面上方气体的压强.求解式(1)，得到

其中

a′=ρg,b′=p+|x|ρg,

对试管顶端面元进行受力分析，如图2所示. 浮沉子受到的水压力为Fwater，浮沉子内气柱产生的压力为Fgas，面元自身重力、面元受到的浮力和侧壁对面元的拉力的合力为Gtube.

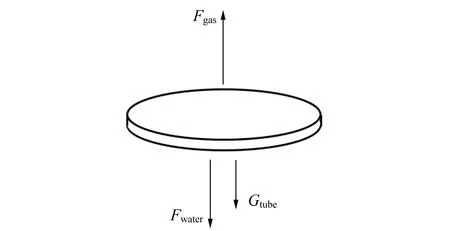
图2 试管顶端面元的受力示意图

令面元所受合力为F，可得：

F=Gtube+Fwater-Fgas,

(2)

其中，

(3)

其中，d0为上方面元厚度，dext和dint分别为试管外径和内径，L为试管长度，ρglass和ρ分别为玻璃和水的密度.式(3)中第一项为浮沉子重力项，第二项为浮沉子所受浮力项.

(4)

(5)

其中，pgas为浮沉子内部气柱的压强.

当考虑浮沉子上端在水下(即x≤0)时，由浮沉子平衡条件得F=0，由式(2)～(5)得：

(6)

分析浮沉子中空气柱的压强，可得：

pgas=p+(ξ+|x|)ρg.

(7)

式(6)和(7)交点的位置坐标即为临界深度，此时为浮沉子可逆下沉与不可逆下沉的分界点.

(8)

其中，

(9)

当浮沉子初始时完全位于液体内部，增大压强将导致|Fwater|>|Fgas-Gtube|，合力向下，导致浮沉子下沉.此时，只要给予浮沉子微小的向下速度，就能够使其发生不可逆下沉，在这种情况下初始位置即为临界深度.

如图1(b)所示，当浮沉子初始时部分位于液体内部时，增大压强即增大了浮沉子向下的压力，浮沉子向下移动，导致向上的合力|Fgas-Gtube|增大，从而达到|Fwater|=|Fgas-Gtube|，浮沉子处于平衡状态.如果不断增压将导致浮沉子的位置不断向下移动.在达到临界深度之前，如果恢复原始压强将导致Fwater减小，而Fgas和Gtube不变，则浮沉子受到向上的合力而向上移动，此时的下沉可逆.

如图1(c)所示，浮沉子初始时处于液体中的某一位置.当这一位置处于临界深度上方时，|Fwater|<|Fgas-Gtube|，浮沉子上浮；当这一位置处于临界深度时，|Fwater|=|Fgas-Gtube|，浮沉子悬浮；当这一位置处于临界深度下方时，|Fwater|>|Fgas-Gtube|，浮沉子下沉.

综上所述，增大浮沉子体系的压强，浮沉子将下沉至某一位置.当浮沉子处于该位置时，恢复初始压强，浮沉子有3种浮沉状态：处于临界深度上方时，浮沉子上浮，此过程称为可逆下沉；恰好处于临界深度，浮沉子悬浮；处于临界深度下方时，浮沉子下沉，此过程称为不可逆下沉.

1.2 浮沉子受迫下沉以及不可逆现象的解释

假设温度不变，忽略浮沉子顶端面元受到的重力和浮力[1]，得到

(10)

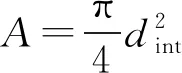
(11)

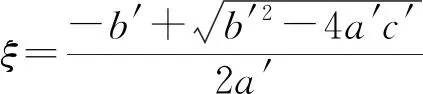
由此，利用Matlab数值模拟可以做出浮沉子势能U(x)与位置x的关系曲线，如图3所示.其中参量取值为：浮沉子的质量m=0.018 63 kg，液体密度ρ=1 ×103kg/m3,浮沉子内气柱的横截面积A=0.000 16 m2,重力加速度g=9.8 m/s2,大气压强p0=1.013×105Pa,浮沉子未放入水中时气柱长度l0=7 cm,组成浮沉子的试管体积V=8.101 5×10-6m3,石英密度ρglass=2.3 ×103kg/m3,浮沉子的总长度L=16 cm.

不同压强条件下的势能曲线如图3所示，当压强逐渐增大时，势能逐渐由类似于三次函数过渡到单调递增的函数；当压强在较小范围内时，浮沉子势能存在1个极大值和1个极小值，图3中的压强为1.025p0时，势能存在极大值Umax和极小值Umin.

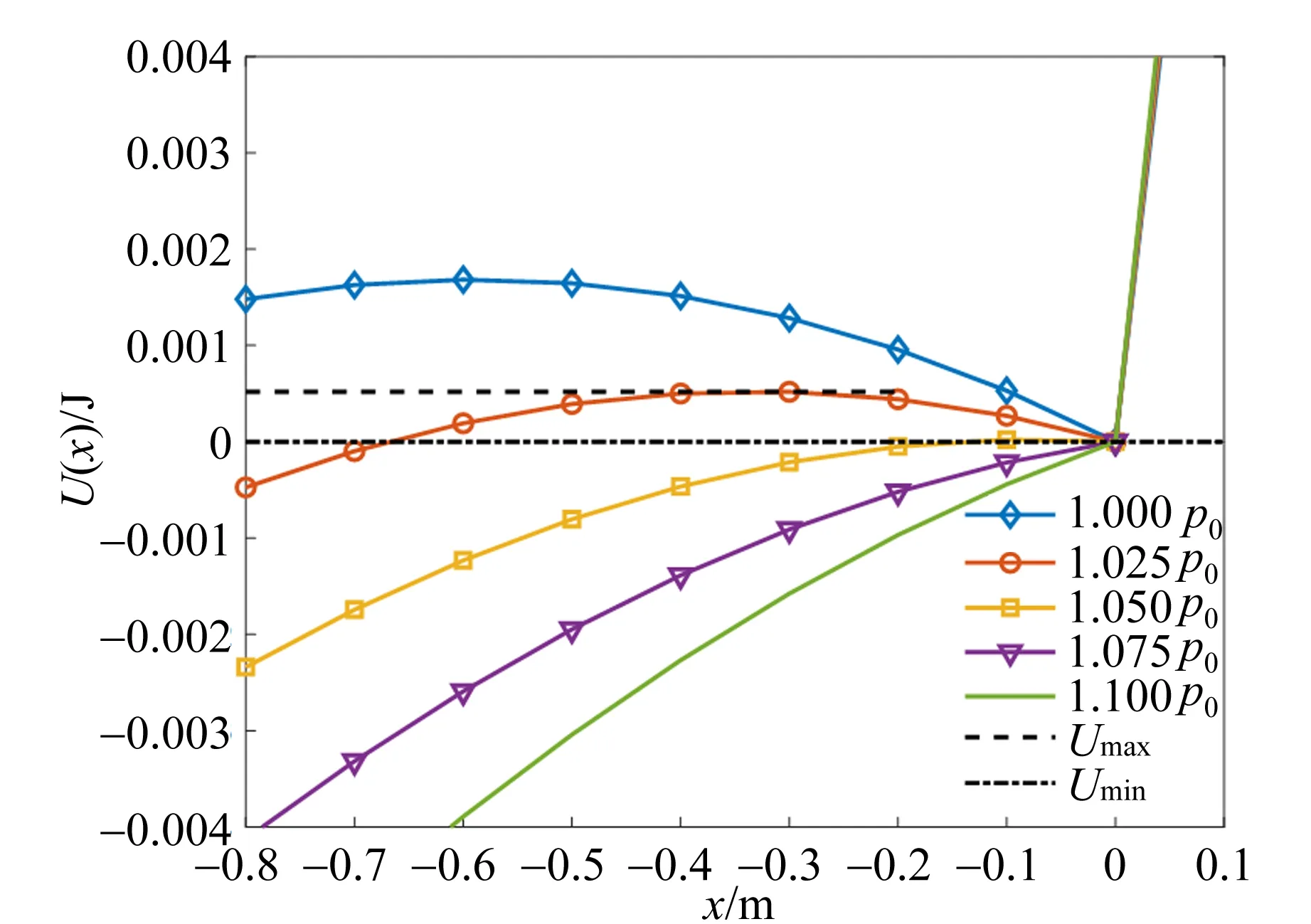
图3 不同压强下浮沉子势能随位置的变化

在势能最大值处浮沉子的受力方向发生改变，如图4所示.

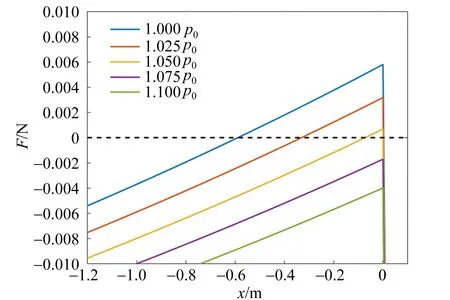
图4 不同压强下浮沉子受力随位置的变化

当压强较大时，受力始终竖直向下，浮沉子只能发生不可逆下沉，如图4中压强为1.100p0的受力曲线.浮沉子体系的增压大小是浮沉子可逆或者不可逆下沉的重要因素.较小的微扰使得浮沉子在稳定平衡点附近做类似谐振子振动，即浮沉子在稳定位置附近往复振动.而较大的微扰会导致浮沉子越过Umax所对应的位置，从而受不稳定平衡点附近运动规律的支配.势能的极小值点对应浮沉子的稳定平衡点，即浮沉子在液面上方的平衡位置.当浮沉子受到较小扰动偏离该位置时，由于浮力作用而回到初始稳定平衡位置.势能极大值点对应浮沉子不稳定平衡位置，浮沉子的受力在此处发生变化：在此位置上方，浮沉子所受浮力大于重力，从而回到其稳定平衡位置，下沉是可逆的；在此位置下方，浮沉子所受浮力小于重力，从而发生不可逆的下沉.

2 实验验证

实验中组成浮沉子的试管为内外径以及长度均不同的石英管，根据实验需要在石英管中有不同长度的水柱. 为了使实验时能够在更大范围内调节相关参量，实验中浮沉子被置于高度为2 m的垂直长管中. 通过将垂直长管密封并连接到流量可控的气泵来控制管中压强.

实验液体为水，重力加速度为9.8 m/s，p0为理想大气压，石英密度为2.3×103kg/m3. 为了探究相关参量，定制仅改变长度或内外径比例的试管，规格如表1所示.

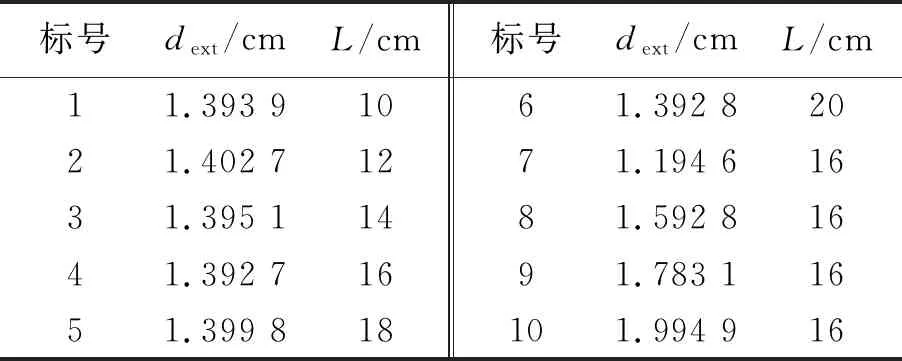
表1 实验中所使用的浮沉子规格

在其他参量保持不变时，测量了临界深度随初始时浮沉子中气柱长度的变化，如图5所示. 测量试管6得到的浮沉子顶端完全浸没时的气柱长度为113.0 mm. 当其他条件保持不变，浮沉子中的初始气柱长度l0增加时，临界深度将会随之线性增加. 这是因为当l0增加时浮沉子在水中受到的浮力将会增大，从而将在更深的位置发生不可逆下沉现象. 当初始气柱从114.0 mm增加到127.1 mm时，不可逆位置从-16.21 cm下降到-141.19 cm.

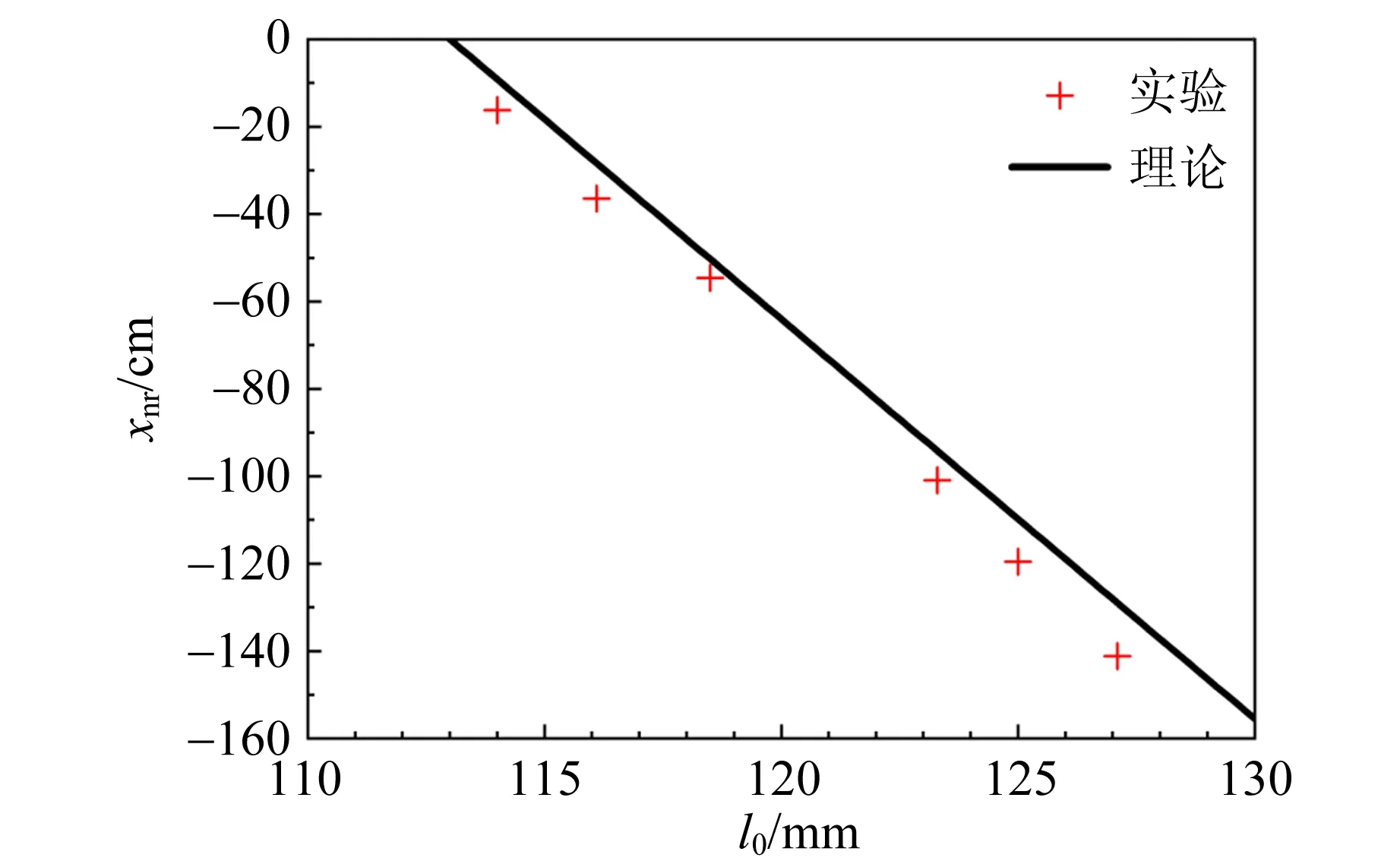
图5 临界深度随初始气柱长度的变化

图6 临界气柱长度与水的密度倒数的关系

使用相同长度、不同内径和外径的试管探究了不可逆参量随外径和内径的比值平方的变化，如图7所示，所用浮沉子为试管4，7，8，9，10. 当外径和内径的比值的平方从1.24增大到1.44时，不可逆参量从4.30 cm增大到7.32 cm. 外径与内径的比值的平方越大，将导致浮沉子玻璃的质量增加，从而浮沉子的气柱中的气体体积变大才能保持平衡状态，因此临界气柱长度随外径与内径的比值的平方增大而增大. 这里实验与理论的数值出现偏差的原因是由试管内外径的测量精度造成的.

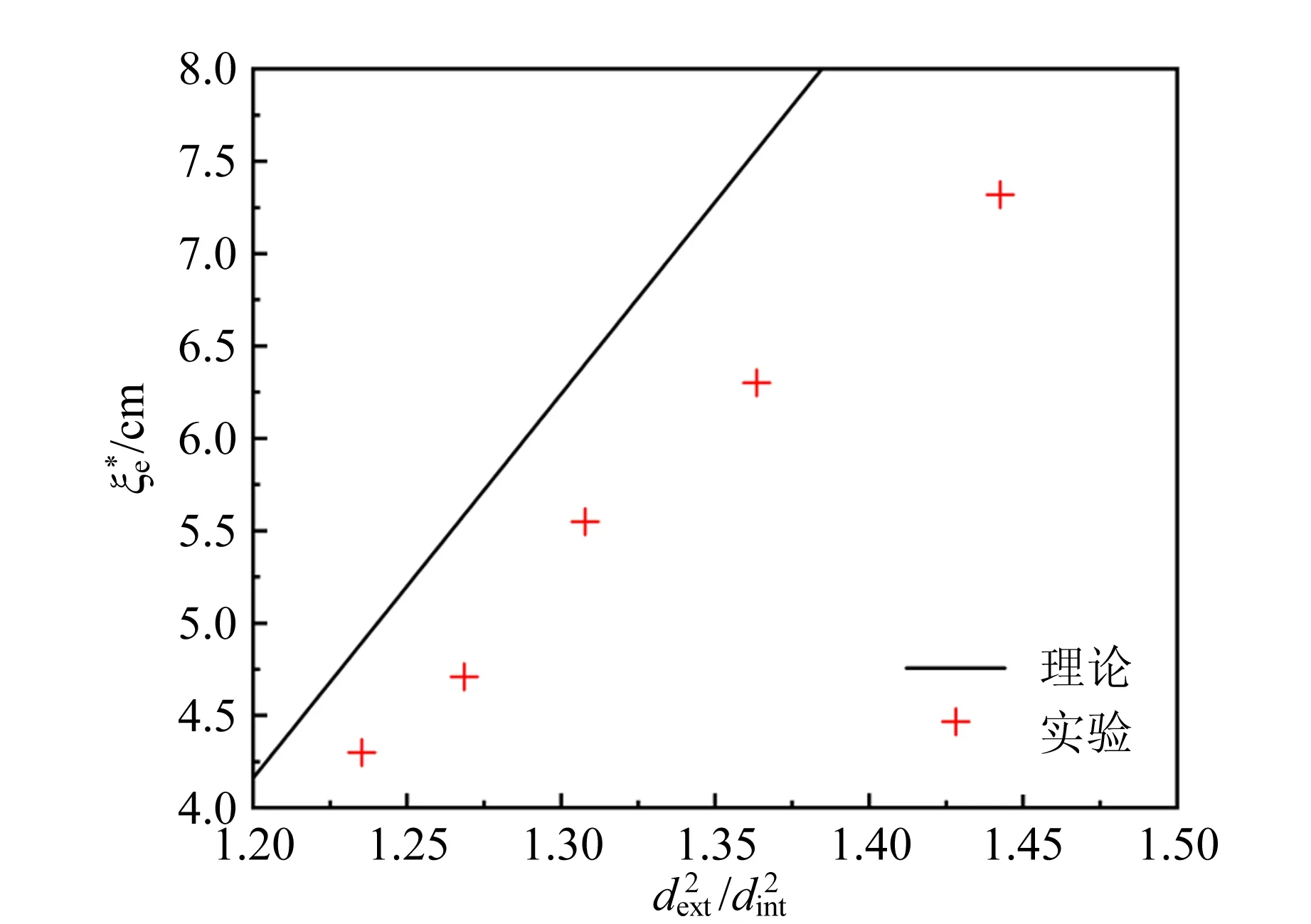
图7 临界气柱长度与外径和内径比值平方的关系

在其他参量保持不变时，探究不可逆参量随试管总长度的变化，如图8所示，所用浮沉子为表1中试管1～6. 当浮沉子长度增大时，需要浸没到较深处才能达到可逆位置. 当试管长度从10 cm增加到20 cm时，不可逆参量从4.54 cm增加到9.10 cm.

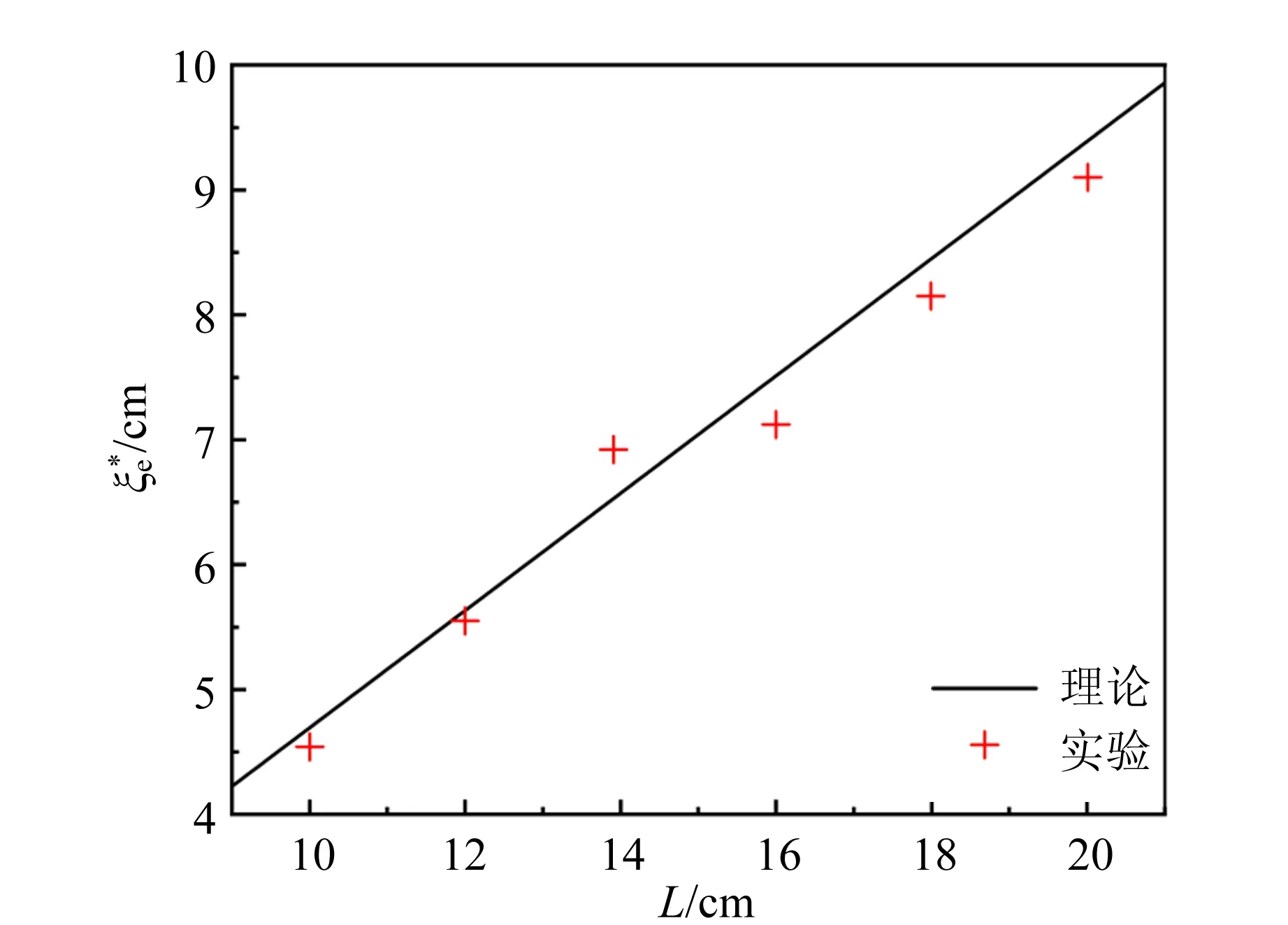
图8 临界气柱长度与试管长度的关系

3 结束语

本文从理论上探究了浮沉子不可逆下沉的临界位置，解释了压强对浮沉子不可逆下沉现象的影响. 浮沉子在液体中存在不稳定平衡的临界位置. 从受力角度解释，是当浮沉子完全浸没时无法依靠增大气体体积而增大浮力所致；从势能的角度解释，该位置是浮沉子的不稳定平衡点，改变压强会导致不可逆平衡点发生改变，进而导致出现不可逆下沉. 另外，通过实验验证了浮沉子不可逆下沉的临界深度与浮沉子未置入水中时的气柱长度、液体密度和试管的外径与内径的比值以及总长度之间的关系，并对实验现象给出了直观的物理图像解释.