基于共模电感的RLC电路非线性动力学研究

苏 籍,白在桥

(北京师范大学 物理学系，北京 100875)

非线性动力学研究兴起于上世纪60年代，从研究对象和方法上扩展了当代物理学的内容，并从观念上改变了人们对经典物理决定论的认识. 将非线性动力学实验引入基础物理实验教学，可以引导学生从动力学的角度认识物理系统，激发学生探索自然规律的兴趣. 由于课时和背景知识的限制，这类实验的教学目标应为使学生认识典型的非线性动力学现象和规律，并了解动力学的研究方法.

非线性动力学的研究对象具有普适性，在不同的物理体系中都有体现. 相比于力学系统，电学系统(混沌电路)具有稳定性好、时间尺度短、便于调节控制参量和数据采集等优点，在非线性动力学实验研究中具有更高的可行性. 最早验证费根鲍姆关于倍周期分岔通往混沌道路普适性的实验就是在非线性电路上完成的[1]，该电路采用变容二极管作为非线性元件. 基于非线性电阻的蔡氏电路(Chua’s circuit)则被广泛应用于科研和教学中[2]. 关于混沌电路的详细介绍可以参考文献[3-7].

上世纪90年代北京师范大学在本科教学中引入非线性动力学实验，其中包括以磁环电感作为非线性元件的混沌电路[8-10]. 该电路含有3个绕组的特制变压器，在电路中3个绕组分别接成直流偏置、无源RLC振子和驱动RLC振子，如图1所示. 选择合适的参量，通过这个电路可以观察到通过倍周期分岔到混沌的过程.

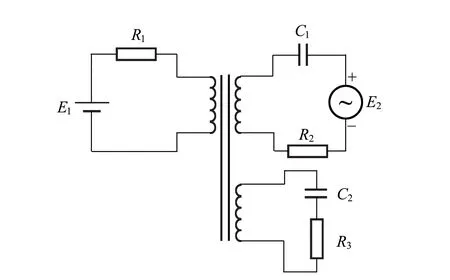
图1 含有3个绕组的变压器非线性电路

本文对该混沌电路进行改进：1)简化电路，省去无源RLC振子部分，同时使用商品共模电感替代特制变压器，便于在教学中推广；2)对电路进行数学建模，该模型可以复现大部分实验现象，从而加深学生对混沌电路原理的理解.

除了倍周期分岔和混沌，改进的电路还可以出现阵发、激变、多吸引子共存等动力学现象，可以更好地应用于基础物理实验教学.

1 实验装置

1.1 共模电感

共模电感本质为1∶1的变压器，如图2所示，常用于滤除电源线的共模干扰. 由于一次和二次绕组的匝数相同，磁场强度H正比流过2个绕组的电流的代数和,即

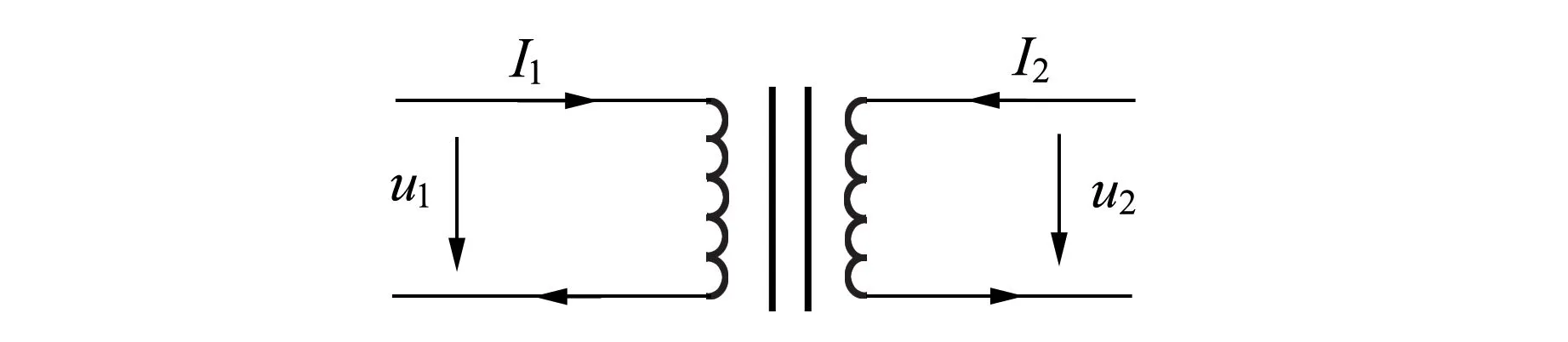
图2 共模电感电路

I(t)=I1(t)+I2(t) ，

(1)

根据电磁感应原理，忽略漏磁，2个绕组的电压为

(2)

其中，Φ(t)为绕组的总磁通量，等于磁环的磁通量与绕组匝数的乘积.对于线性电感，在任意时刻Φ和I都成正比，即Φ(t)=MI(t)，根据式(1)和式(2)，可以得到

(3)

其中，比例系数M为每个绕组的自感量或它们之间的互感量(忽略漏磁，则二者相等).但实际磁环材料存在饱和与磁滞现象，这是共模电感元件非线性的来源.值得注意的是，磁滞现象意味着Φ(t)与I在t时刻之前的变化历史有关，一般不能写成I(t)的单值函数.

在一次绕组中通入交流周期电流I1(t)，测量二次绕组的开路电压u2(t)，采用傅里叶变换计算其积分得到Φ(t).图3所示为不同电流幅度 (频率为750 Hz)的7条实测Φ-I关系曲线.

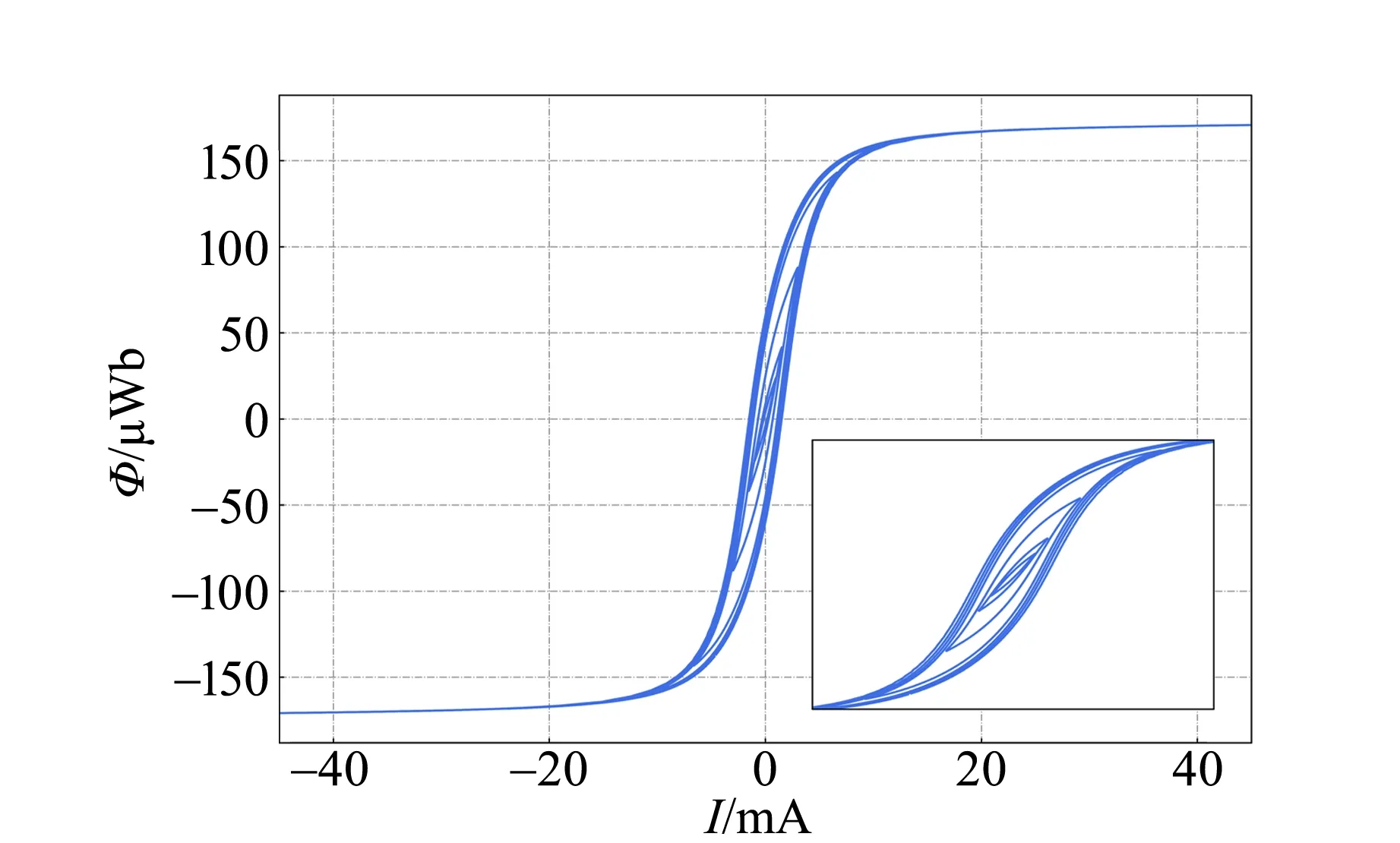
图3 实测共模电感特性(插图为曲线局部放大图)

这些曲线经过适当的标度后就是磁环材料的磁滞回线[11].从图3中可以看出磁滞回线很窄，表明磁环为软磁材料，而且mA量级的电流可以产生明显的饱和现象[作为滤波元件时，I1(t)和I2(t)基本反相，I(t)很小].

1.2 实验电路

改进的实验电路如图4所示，其中，E1为直流电源，E1/R1称为偏置电流；E2为正弦信号发生器，输出波形为激励信号，其峰峰值记为Vpp.为了减小信号发生器的输出阻抗，激励信号需要经过功率放大器(图中未画)再接入电路.

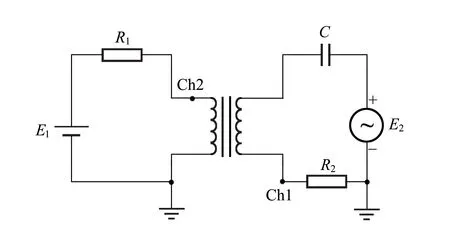
图4 非线性RLC电路

实验中，用示波器通道1观察R2两端的电压v2(t)(与回路电流成正比)，通道2观察一次绕组的感应电压u1(t).在不严格的意义下，下文称用XY方式显示的曲线为轨迹图.

2 实验现象与分析

典型非线性动力学现象具有结构稳定性，因此电路元件取值(在一定范围内)并不影响实验效果.本节实验现象是在R1=10 kΩ，R2=4.1 Ω，C=9.4 μF，E1=24 V，f=750 Hz时得到的.逐渐升高Vpp，系统会表现出与一维logistic映射相似的混沌带与周期窗口相互嵌套的复杂结构[12]. 图5所示为有代表性的轨迹图(图5由示波器保存的数据绘制).

2.1 通过倍周期分岔达到混沌

电阻和磁环(由于存在磁滞)都会把电能转换为热能，因此本实验电路是耗散系统. 倍周期分岔是耗散系统中最常见的通往混沌的道路，图5(a)～(f)体现了该过程. 理论上倍周期分岔可以一直进行下去，由于信号源调节以及数据采集的精度有限，再加上电路噪声的影响，实验上只看到了4次倍周期分岔.

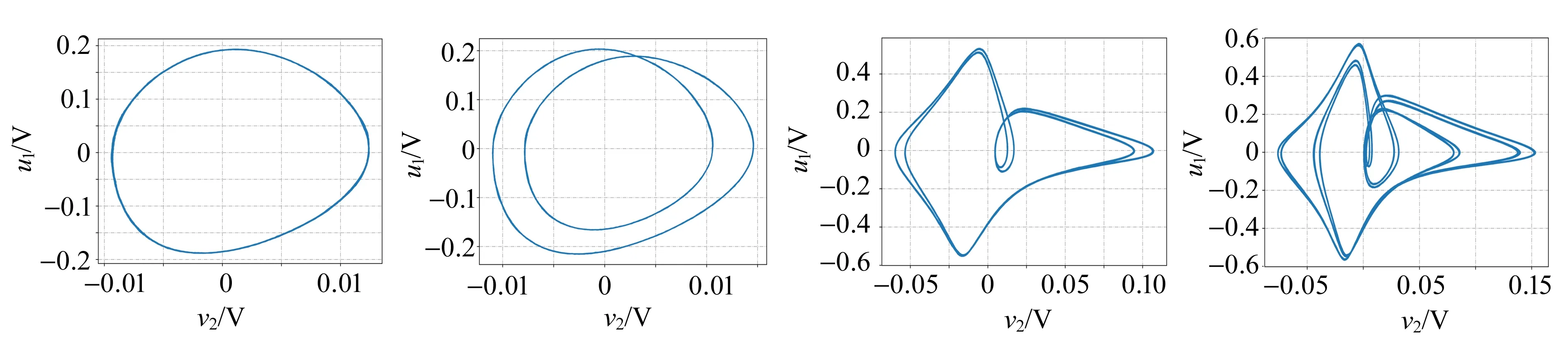
(a)Vpp=167 mV,1周期 (b) Vpp=254 mV,2周期 (c) Vpp=521 mV,4周期 (d) Vpp=534 mV,8周期

2.2 周期窗口

继续增大Vpp，电路出现一系列稳定的周期轨道，如图5(g)～(j)所示. 实验上可以找到周期数从3到10(相对驱动信号周期)的初级(不是某个倍周期分岔的产物)周期轨道. 相反，每条初级周期轨道都会随着Vpp的增大而发生倍周期分岔，从而形成一段规则运动的窗口. 相邻的初级周期窗口之间为混沌带.

图5 (g)和5(j)都是5周期轨道，但是这2条轨道的特征存在明显区别：前者的v2在1个周期内出现了3个正向大尖峰和1个负向尖峰，而后者有4个正向尖峰和3个反向尖峰，具体如图6所示.

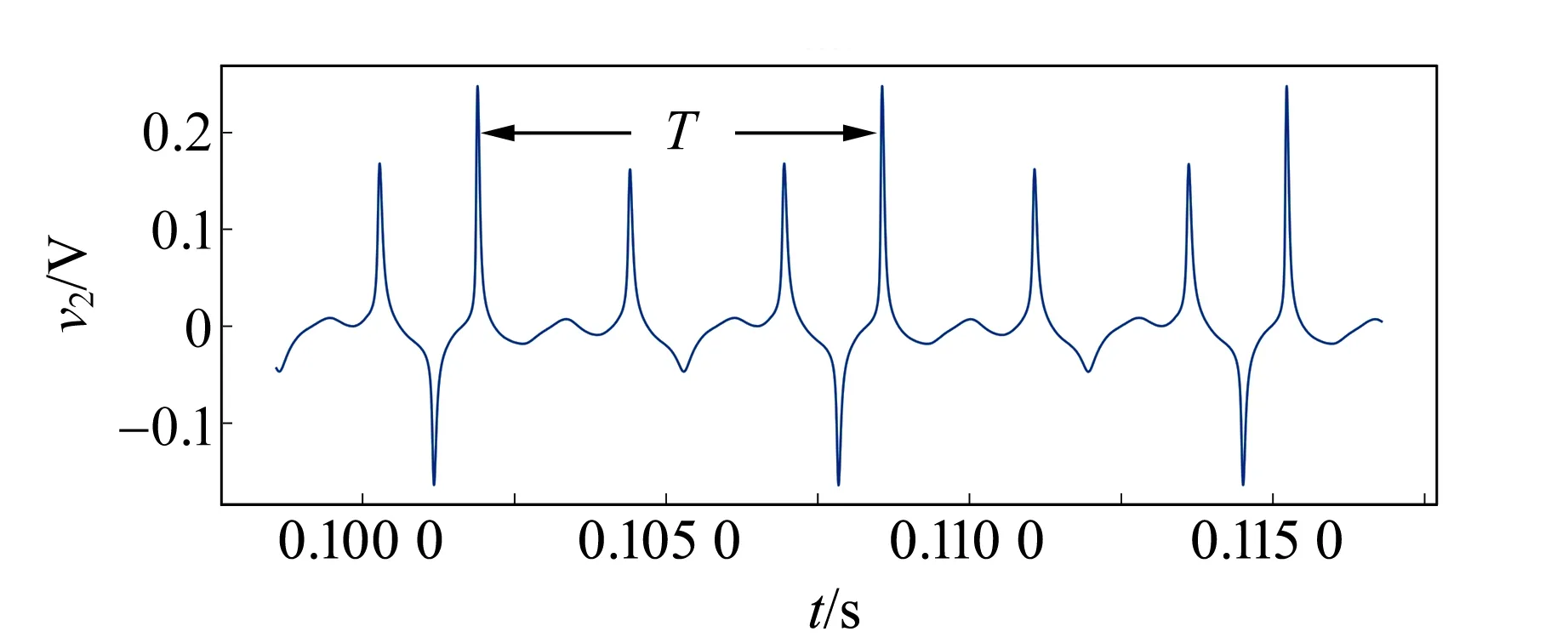
(a)Vpp=593 mV

表1为部分代表性轨道以及特征. 表1中n*2m表示初级n周期轨道经过m次倍周期分岔后的轨道.

表1 部分代表性轨道及特征(f=750 Hz)

2.3 阵发

当Vpp不断增加，系统最终会归于如图5(l)所示的1周期轨道. 此时如果降低Vpp，系统会连续返回如图5(k)所示的混沌状态. 这里从规则变化到混沌的过程是通过阵发实现的. 阵发的特点是大部分时间轨道看起来是规则的，但偶尔会插入一段不规则的运动，如图7所示.

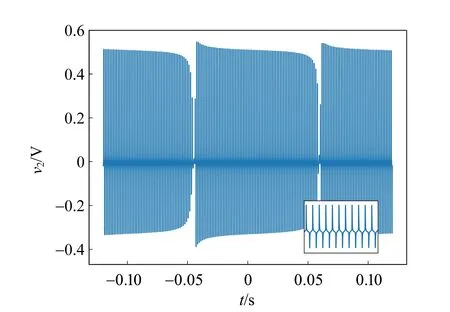
图7 阵发轨道的电流波形(Vpp=827 mV)

随着Vpp趋向临界值，规则片段(图7插图)的长度趋于无穷，最终回到周期轨道. 事实上，每条初级周期轨道都是通过阵发的形式从混沌带的边缘产生，其中最后的阵发过程最为明显.

2.4 激变

激变是有别于倍周期和阵发的另一种常见的通往混沌的道路[13]. 激变的含义：在参量接近阈值之前，系统处于混沌状态，而超过阈值后，原来的混沌轨道成为瞬态，最终会离开该区域，进入相空间的另一部分. 与阵发不同的是，激变属于全局分岔，当扫描参量接近突变点时，激变的轨道一直保持无规则状态，不会出现长时间的规则片段.

在E1=12 V,f=650 Hz时可观察到激变现象.逐渐增加Vpp，在Vpp=636 mV时系统还处于混沌状态，如图8和9(a)所示.当Vpp=637 mV时，吸引子突变为周期轨道，如图9(b)所示，表明Vpp在636～637 mV之间，电路发生了激变.此外，当Vpp超过临界值到达周期轨道之后，再逐渐减小Vpp，由上向下经过突变点，周期轨道并不会立即变成混沌轨道，即激变是不可逆的. 继续减小Vpp，周期轨道可以保持到Vpp= 610 mV，然后在Vpp= 609 mV时突变为混沌轨道，时间波形图和轨迹图与图8和图9(a)相似.

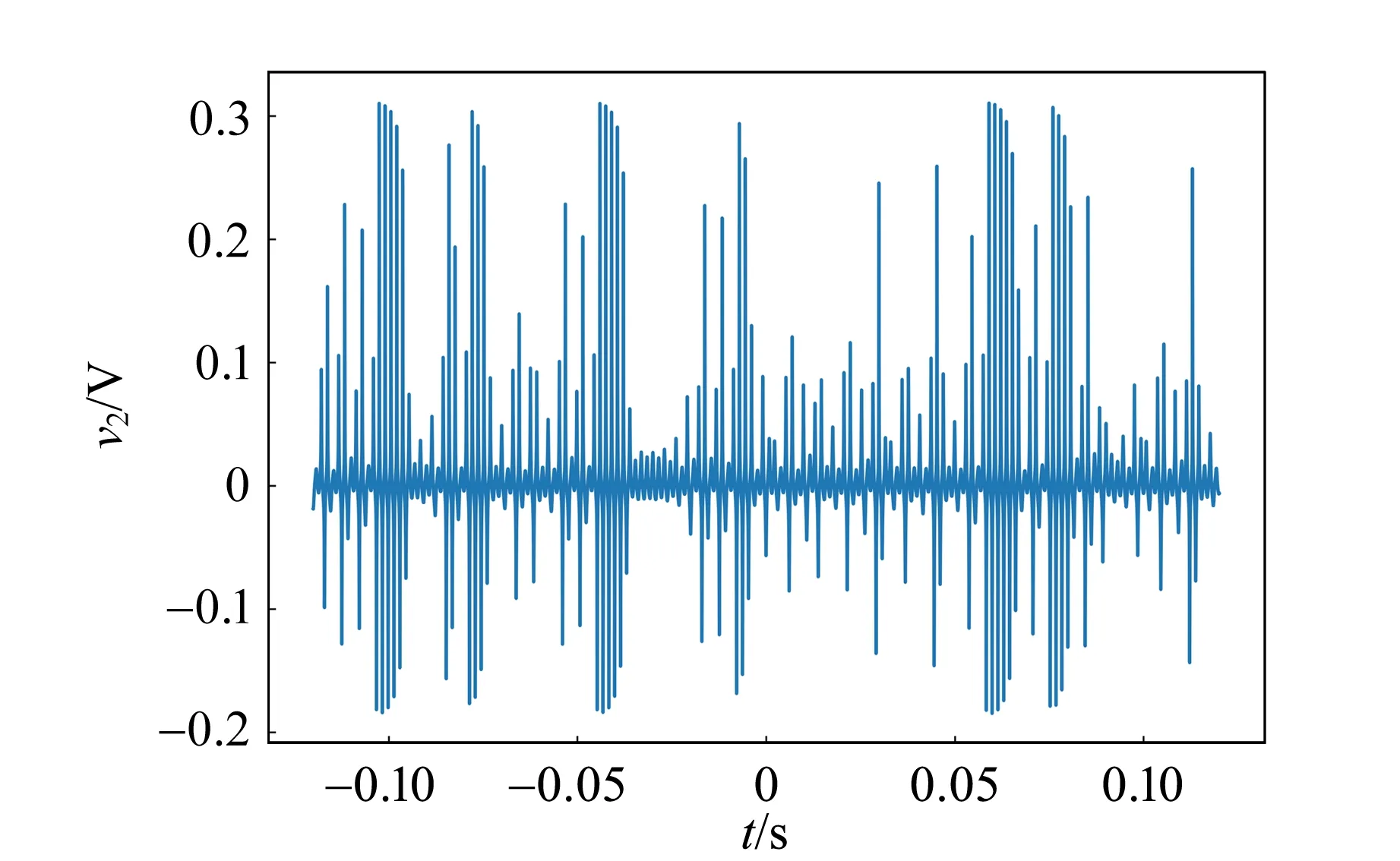
图8 激变前的混沌轨道(Vpp=636 mV)

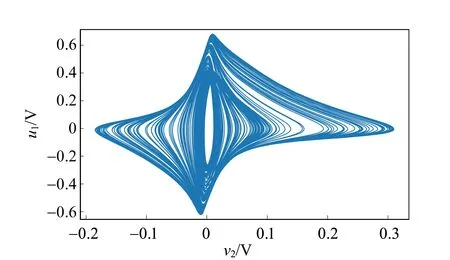
(a)Vpp=636 mV

根据上述现象可以推出：如果Vpp在610～636 mV之间，电路存在2个稳定状态(吸引子)：周期轨道和混沌吸引子. 事实上，如果施加扰动(例如关闭信号源再迅速打开)，可以让电路稳态以一定概率在这2个吸引子之间跳转. 多吸引子同存是非线性系统中的常见现象.

最后需要说明的是，如果Vpp保持合适取值，连续降低激励信号的频率，也可以出现类似的分岔和突变现象.

3 理论分析

3.1 数学建模

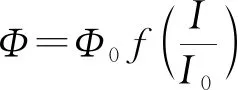
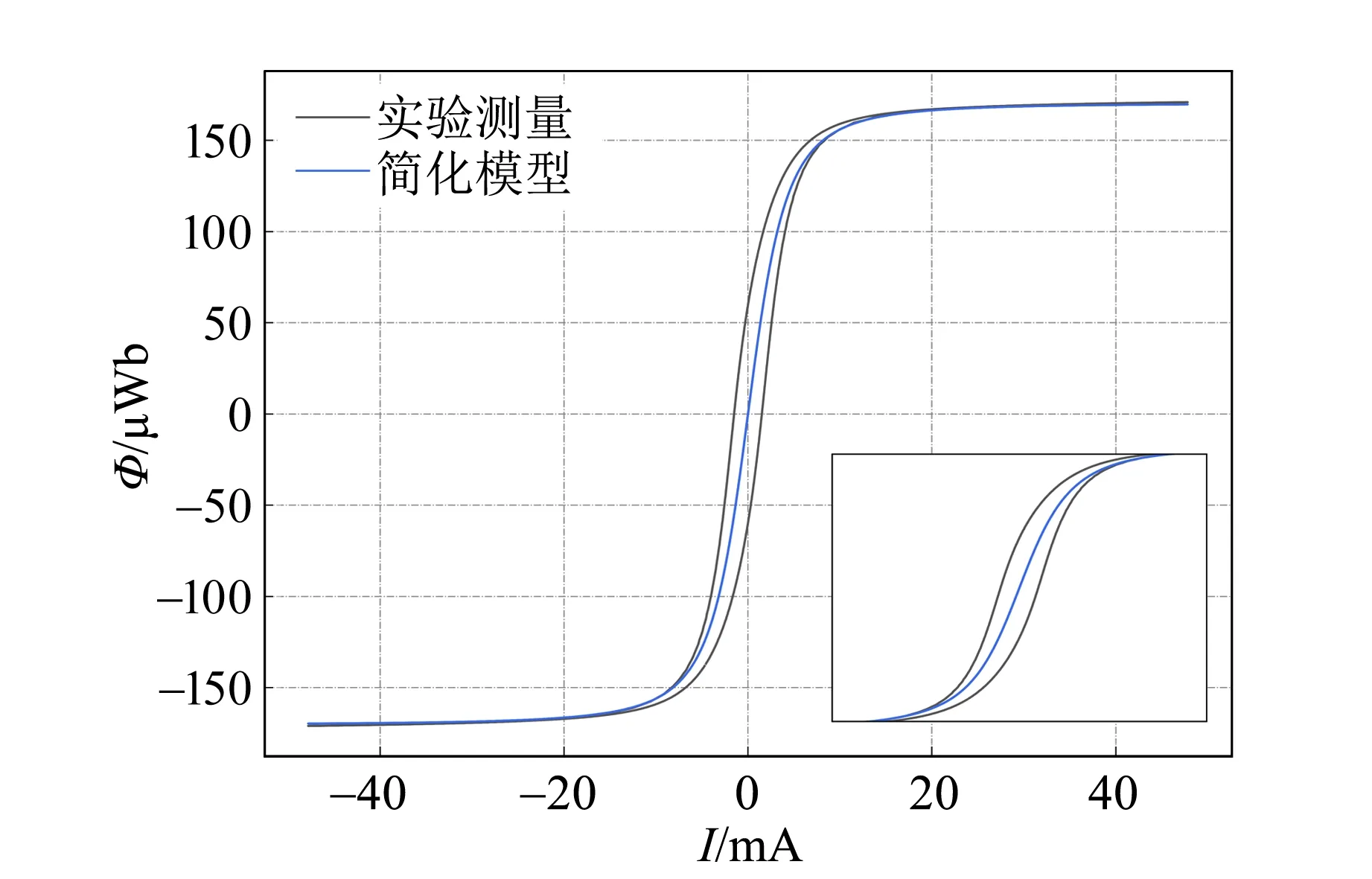
图10 实验与拟合的磁通量与电流关系

(4)

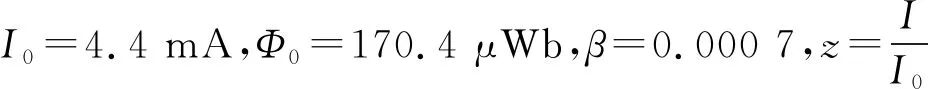
下面基于简化的共模电感模型分析电路.为方便起见，首先进行无量纲化[14]，取I0=Φ0=C=1，因此电压和角频率为

其中1/ω0为时间的单位，电阻为

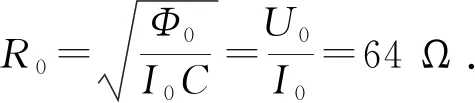
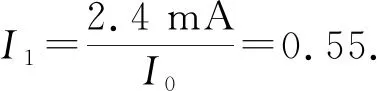
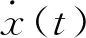
(5)

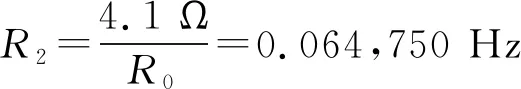
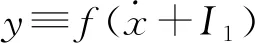
(6)

其中，Δ≡I1,ν≡R2.式(6)即为描述电路的简化微分方程.

3.2 模拟结果及分析

为了与图5和表1的结果对比，在数值模拟中取Δ=0.55，ω=2.88.考虑到磁滞损耗以及功率放大器的输出阻抗，ν略微高估为0.1，A为可调整参量.注意与A等效的Vpp表示为

Vpp=2AU0.

(7)

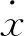
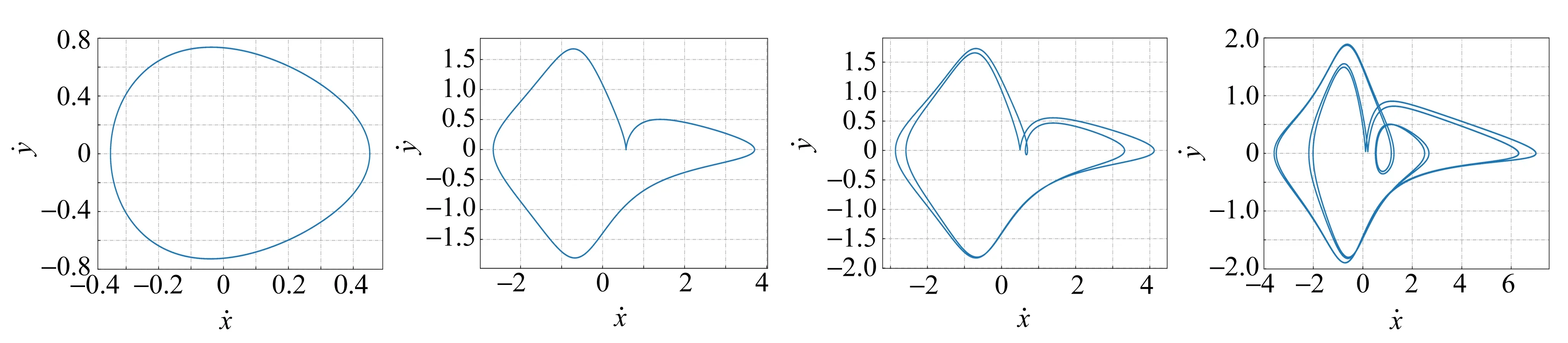
(a)A=0.600,1周期 (b) A=0.620,2周期 (c) A=0.755,4周期 (d) A=0.794,8周期

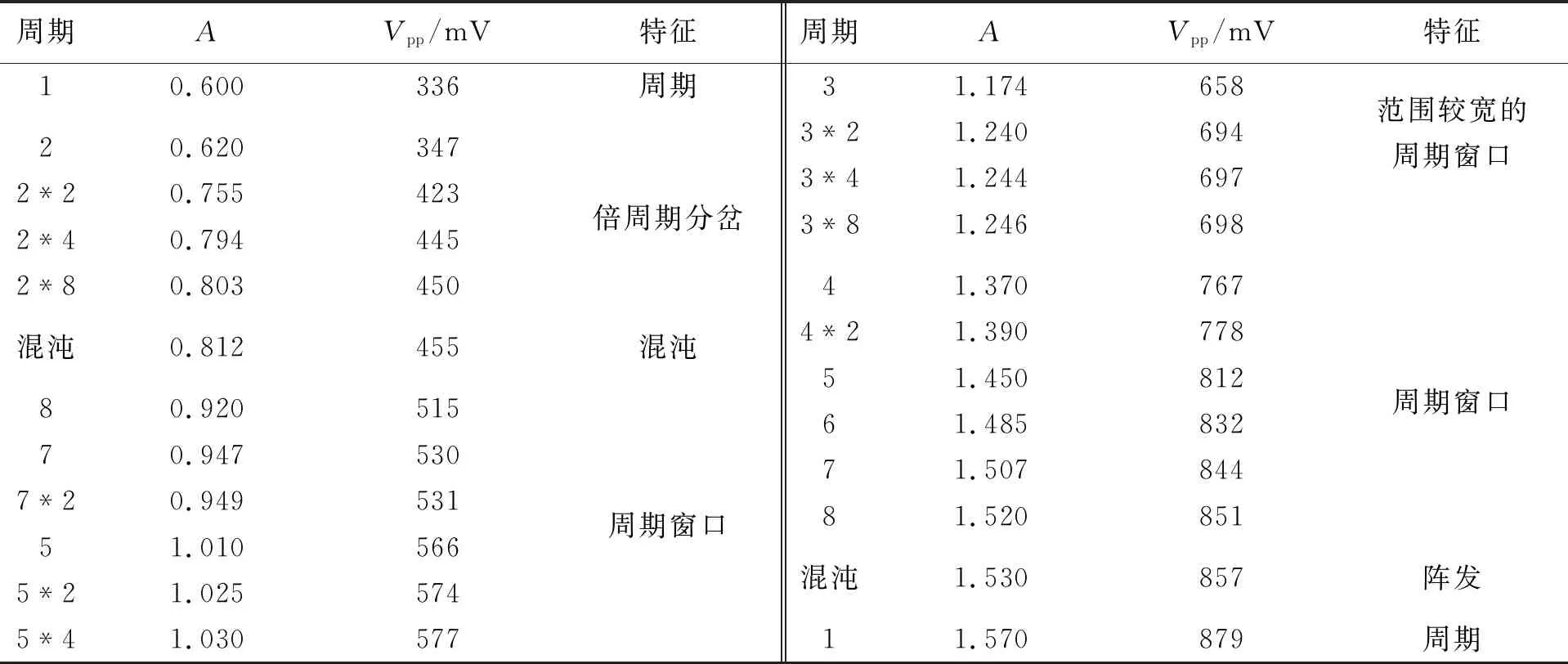
表2 简化模型代表性轨道及特征

模型与实验最明显的区别是：随着Vpp增大，模型中的1周期轨道经过了1次突变(失稳) 直接跳到2周期轨道，中间并没有发生倍周期分岔. 然后从2周期轨道开始，发生了通过倍周期分岔到混沌的转变. 实验上，虽然开始的2周期轨道[图5(b)]和4周期轨道[图5(c)]的形态相差很大，但在连续改变Vpp的过程中，轨道的形态变化是平滑且可逆的. 另外，对比表1和表2，可以发现模型和实验中相同动力学现象对应的参量值也存在差距. 但是模型可以复现大部分实验中发现的动力学现象. 这表明仅考虑共模电感的饱和行为就可以解释电路的主要非线性动力学行为.

4 结束语

本文对包含非线性电感的混沌电路进行了简化，并根据实测数据对电路进行了简化建模. 实验发现，通过调节激励幅度或频率，该电路可以产生倍周期分岔、混沌带中周期窗口、阵发、激变与多吸引子共存等典型的非线性动力学现象. 而数值仿真也发现忽略磁滞效应的简化模型可以复现大部分实验现象. 该电路结构简单，制作成本低，易于在教学中使用，且动力学现象丰富，教学内容选择自由度大，可以作为大学物理实验中的RLC串联谐振电路的自然推广.