破解外接球问题三法:定义,构造,交轨
湖北省大冶市实验高中 石晓皎
1 引言
空间几何体的外接球问题,其问题创设的形式各样,变化多端,是一类常考常新的综合应用问题.解决问题时,关键是利用空间几何体的结构特征,以及外接球的定义、性质等,确定空间几何体外接球的球心位置或球的半径.下面结合具体案例,从球的定义(定义法)、几何体的结构特征(构造法)以及球的性质(交轨法)等视角来分析与处理空间几何体的外接球问题,并巧妙归类与总结.
2 破解三法
2.1 定义法
通过题目中所给的空间几何体的结构特征,结合球的定义确定其外接球的球心位置或半径.其实就是抓住球的定义本质进行求解.

A.72π B.144π C.50π D.100π
分析:根据给定条件,取PC中点O,结合线面垂直的判定与性质,利用直角三角形的性质,结合球的定义来确定四棱锥P-ABCD外接球的球心位置,进而构建关系式计算出球半径,代入球的表面积公式计算即可.

图2
解析:四棱锥P-ABCD的底面是矩形,取PC中点O,连接AC,OA,OB,OD,如图1所示.
因为PA⊥平面ABCD,BC⊂平面ABCD,则PA⊥BC.而AB⊥BC,AB∩PA=A,AB,PA⊂平面PAB,则有BC⊥平面PAB.
又PB⊂平面PAB,所以BC⊥PB.
同理,可证CD⊥PD.
而PA⊥AC,因此
结合球的定义,可知四棱锥P-ABCD外接球的球心为O,半径为OA.
在矩形ABCD中,AC2=AB2+BC2,从而得
即球半径OA=5,所以四棱锥P-ABCD外接球的表面积为S=4π×52=100π.
故选择答案:D.
点评:定义法确定空间几何体外接球的球心位置或半径,其实就是抓住球的定义这一实质,利用球心到球面上任意一点的距离都相等,巧妙综合空间几何体的对称性、平面几何图形的基本性质等,结合球的定义巧妙构建相应的关系式,实现问题的化归与应用的目的.
2.2 构造法
通过题目中所给的空间几何体的结构特征,巧妙构造立体几何模型,如所给空间几何体是柱体、锥体等,可构造长方体或正方体等特殊立几模型来转化与应用.

分析:如图2,连接AO,并延长交BC于点D.由顶点P在底面的射影O为△ABC的垂心,可得BC⊥PA,AC⊥PB,AB⊥PC.由S△ABC·S△OBC=S△PBC2,可得△POD∽△APD,PA⊥PD.即可得PA,PB,PC两两互相垂直.通过构造立体几何模型法,利用三棱锥P-ABC的外接球为以PA,PB,PC为棱的长方体的外接球,即可建立涉及外接球半径的关系式,结合三角形的面积公式以及基本不等式的应用来转化与应用.

图2
解析:如图2所示,连接AO并延长交BC于点D,连结PD.
由于顶点P在底面的射影O为△ABC的垂心,则知AD⊥CB.
又PO⊥平面ABC,可得PO⊥BC.
又AD∩PO=O,所以BC⊥平面APD,可得BC⊥AP,BC⊥PD.同理AC⊥PB.
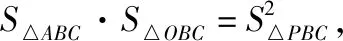
又∠PDO=∠PDA,则有△POD∽△APD,所以∠APD=∠POD=90°,即PA⊥PD.
又PA⊥BC,BC∩PD=D,所以AP⊥平面PBC,而PB⊂平面PBC,故PA⊥PB.
又PB⊥AC,且AP∩AC=A,所以PB⊥平面APC,而PB⊂平面APC,故PB⊥PC.
所以PA,PB,PC两两互相垂直.
所以三棱锥P-ABC的外接球为以PA,PB,PC为棱的长方体的外接球.
设三棱锥P-ABC的外接球半径为R,则有PA2+PB2+PC2=4R2.
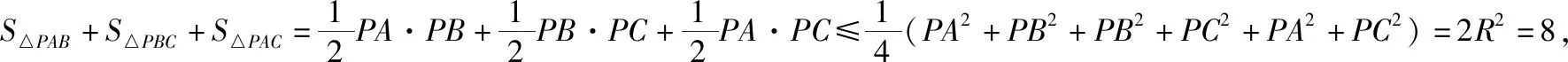
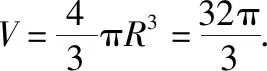
点评:构造法确定空间几何体的外接球的球心位置或半径,其实就是借助补形思维,通过合理补形等方式构造特殊的空间几何体——正方体或长方体等,利用原几何体与所构造的特殊空间几何体的外接球一致,合理转化,快捷处理,进而利用正方体或长方体外接球的球心是其体对角线的中点(体对角线恰是该外接球的直径)来解决问题.
2.3 交轨法
通过题目中所给空间几何体的结构特征,结合外接球的几何特征,从不同视角确定球心所在的直线,而满足条件的两条相交直线的交点就是对应的外接球球心.

分析:根据题目条件,利用交轨法求解.先求出到A,B,C三点等距离的点的轨迹是直线MN,再求出到P,B两点等距离的点的轨迹是直线DE,则直线MN与直线DE的交点即是三棱锥P-ABC外接球的球心,进而结合余弦定理、正弦定理加以分析与求解,确定外接球的半径,即可求解对应的表面积.
解析:设M为BC的中点,在平面PBC内过点M作MN⊥BC交PB于点N.
因为平面PBC⊥平面ABC,所以MN⊥平面ABC.
又三角形ABC是以BC为斜边的直角三角形,所以直线MN上任意一点到A,B,C三点的距离相等.
在平面PBC内作线段PB的垂直平分线DE,设DE与MN的交点为O,则点O到P,A,B,C四点的距离都相等,即点O为三棱锥P-ABC外接球的球心,并且点O也是三角形PBC的外心.
因此,三棱锥P-ABC外接球的半径与三角形PBC外接圆的半径相等.
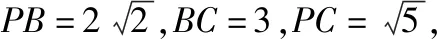
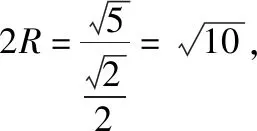
所以,三棱锥P-ABC外接球的表面积S=4πR2=10π.
故填答案:10π.
点评:交轨法确定空间几何体外接球的球心位置或半径,其实就是借助球的相关性质:“球心O与截面圆的圆心O1的连线垂直于截面圆”“球心O与弦中点的连线垂直于弦”等,利用满足条件的两条相交直线的交点直接确定空间几何体外接球的球心.
3 结语
解决空间几何体的外接球问题,除了以上借助球的定义(定义法)、几何体的结构特征(构造法)以及球的性质(交轨法)等方法来解决外,还可以结合空间坐标法、向量法以及其他一些相关的技巧来处理,关键就是要“心中有图”,正确进行空间想象,构建不同元素之间的联系,合理数学运算,巧妙逻辑推理,实现数学运算、直观想象以及逻辑推理等核心素养的培养与提升.

