立体几何中二面角问题的解法例析

江苏省淮安中学 丁 军

1 向量法

向量法，是指将待求的两个平面放入直角坐标系中，通过向量的知识(例如向量的夹角公式等)进行求解的方法，是求解二面角问题最有效的方法之一.利用向量法求解，避免了添加辅助线作二面角的平面角的麻烦，有效降低题目难度.利用向量法解题的主要步骤：①根据题设找出三条相互垂直的直线建立空间直角坐标系，这是正确求解的关键之一；②将待求的两个平面上的点的坐标及每个面的法向量表示出来；③计算向量的坐标，并利用向量的夹角公式计算，最后还需注意判断二面角的平面角和两个法向量的夹角之间的关系，结合实际图形判断所求角是钝角还是锐角[1].

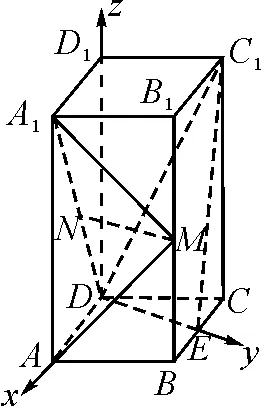
图1

例1直四棱柱ABCD-A1B1C1D1的底面是菱形，已知AA1=4,AB=2,∠BAD=60°，BC,BB1,A1D的中点分别是E,M,N，求二面角A-MA1-N的正弦值.

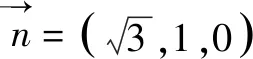
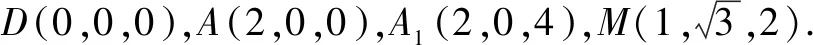
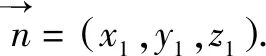
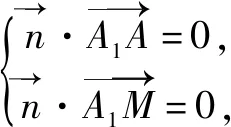
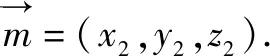
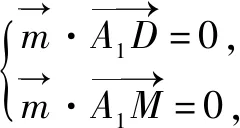
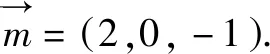
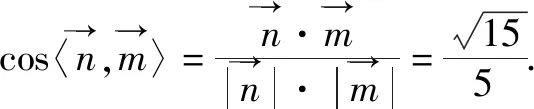
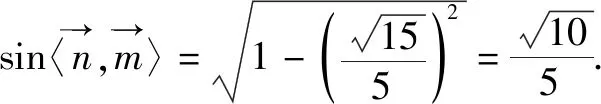
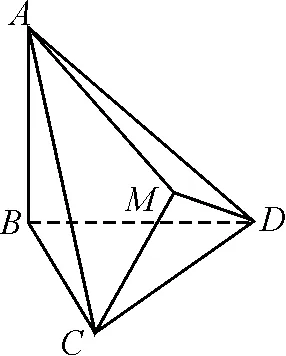
图2

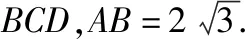
(1)求直线AM与平面BCD所成的角的大小；

(2)求平面ACM与平面BCD所成的二面角的正弦值.

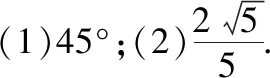
2 定义法

定义法是指利用二面角的定义进行求解的一种方法.从一条直线出发的两个半平面所组成的图形就叫做二面角.一般利用二面角的平面角度量二角面，二面角的平面角是多少度，就说这个二面角是多少度(平面角的取值范围是0°≤θ≤180°).二面角的定义也是求解二面角问题的有效手段，关键在于正确找出二面角的平面角.利用定义法解题的主要步骤：①根据题意作辅助线，准确找出二面角的平面角；②根据题设条件证明上述角是二面角的平面角；③根据题意利用余弦定理等公式计算求解.简要概括为“一作、二证、三计算”.

图3

例2在四面体ABCD中，AC=AB=1，CD=BD=2，AD=2.5，BC=1.5，求二面角A-BC-D的余弦值.

分析:如图3所示，设E为BC的中点.选择辅助线AE，DE，然后利用二面角的定义确定角A-BC-D的平面角为∠AED，再分别计算线段AE，DE的长度，利用余弦定理进行求解.

解析:设线段BC的中点是E，连接AE，DE.

由AC=AB=1，CD=BD=2，可得

AE⊥BC，DE⊥BC.

所以∠AED是二面角A-BC-D的平面角.

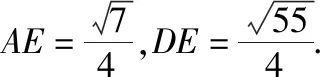
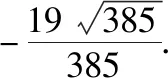
拓展：如图4,在四棱锥P-ABCD中，ABCD是正方形，PA⊥平面ABCD，PA=AB=a，求二面角B-PC-D的大小.

图4

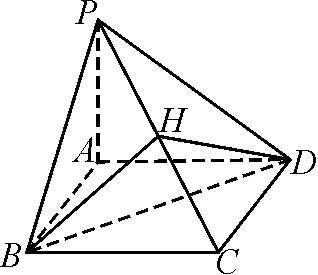
图5

3 垂面法

求解二面角问题的常用方法还包括垂面法.垂面法，就是指作一个与二面角的棱垂直的平面，该垂面与二面角两半平面相交得到交线所成的角为二面角的平面角.适用于锐二面角或直角二面角问题.利用垂面法解题的主要步骤：①根据题意作出与棱垂直的平面；②结合实际问题找出二面角的平面角；③证明上述平面角为二面角的平面角并求出其大小[2].

图6

例3在平面角等于60° 的二面角α-l-β中有一点P，点P到α，β的垂线段长分别为PC=3 cm，PD=5 cm，求点P到棱l的距离.

分析:如图6所示，本题所选择的垂面为平面PCD，进而确定二面角α-l-β的平面角为∠CED=60°，最后根据l⊥平面PCED，得l⊥PE，PE即为点P到棱l的距离.

解析:设过P，C，D三点的平面分别交平面α，β于CE，DE.易证l⊥平面PCD.

∴l⊥DE，l⊥CE.

∴∠CED即为二面角α-l-β的平面角.

∴∠CED=60°，∠CPD=120°.

由余弦定理，可知CD=7.

∵l⊥平面PCED，

∴l⊥PE.

∴PE即为点P到棱l的距离.

又∵P，C，E，D四点共圆，∠PCE=90°，

∴PE是该圆的直径.

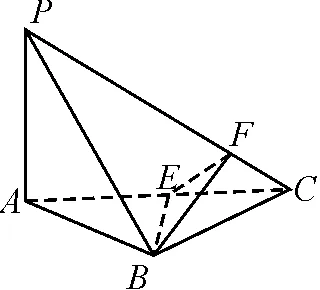
图7

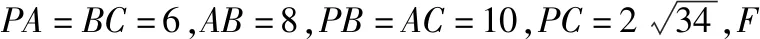
(1)求证：PC⊥平面BEF；

(2)求二面角C-BE-F的大小.

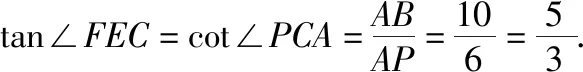
求解二面角问题是高中数学的重要内容，在全国各地高考数学试卷中也经常出现，求解二面角的方法中，笔者认为最简单且最普遍适用的方法莫过于向量法，只要合理建系，正确计算求解即可.