基于APOS理论的数学概念形成教学方式
——以“复数的概念”教学实录与反思为例*
董荣森
(江苏省怀仁中学 214196)
1 基本情况
1.1 授课对象
学生来自省级重点中学高二普通班,基础相对来说比较好,具有一定的自主学习能力、逻辑推理能力、数学运算能力以及数学语言表达能力.
1.2 目标要求
(1)通过解方程遇到具体问题认识复数,理解引入复数的必要性;了解数系的扩充过程:自然数—整数—有理数—实数—复数.
(2)认识虚数单位,掌握复数概念,实部、虚部相关概念,理解两个复数相等的充要条件,提升逻辑推理及数学运算等数学核心素养.
(3)类比有理数集和实数集的关系,认识实数集和复数集的关系,理解实数是复数的一种形式;通过从实数集到复数集的扩充过程和方法,提升抽象概括及逻辑推理素养.
2 设计理念
本节课的设计以杜宾斯基等人创立的APOS理论为基础与依据,紧紧围绕活动(Action)、过程(Process)、对象(Objcet)、图式(Schema)等四个阶段设计教学,选择数学概念形成的教学方式(图1).即通过创设丰富典型的例证性情境,激发学生进行操作或活动,发现真问题(情境驱动、活动阶段);引导学生自主探究提出问题,抽象问题的本质属性,形成初步概念(主体活动、过程阶段);组织学生合作构建,促进深度学习分析问题,对概念的深化与理解(立体互动、对象阶段);强化知识迁移,运用概念解决问题,形成智慧(智慧灵动、图式阶段)进行课堂教学,努力让学生建构复数的概念.

图1
3 教学实录
3.1 创设情境、发现问题(活动阶段)

问题1负实数到底能不能开平方呢?即方程x2+a=0(a>0)有没有解?
生1:在实数范围内不能开平方;在实数范围内没有解.
评析通过创设数学文化情境,设置适合学生认知的问题引发其思考,引导其身临其境地去感受数学家们勇于探究、勇于创新的精神,体会数系的每次扩充都与实际需求密切相关,感受人类理性思维在社会发展中的作用.
3.2 自主探究、提出问题(过程阶段)
师:我们知道x2+1=0在实数集中无解,联系从自然数集到实数集扩充的过程,你能给出一种方法,适当扩充实数集,使这个方程有解吗?
活动1 理解数系的扩充是生产实践与社会发展的需要.
师:通过预习与查阅资料,你能叙述一下数的发展史吗?
生2:因为计数的需要,所以产生了自然数.
生3:为了表示具有相反意义的量引入负数,于是数集由自然数集扩充为整数集.
生4:为了测量与分配的需要,引入了分数,于是数集由整数集扩充为有理数集.
生5:第一次数学危机使人们发现了无理数,于是数集由有理数集扩充为实数集.
师:你遇到过在实数集范围内解不了的方程吗?
生6:遇到过,如一元二次方程ax2+bx+c=0,当Δ=b2-4ac<0时,方程无解.
评析让学生对数集扩充的历史有所了解,感受数学的发展是生产实践与社会发展的需要;让学生从已有的学习经验中自主探究实数集扩充的必要性.
活动2 理解数系的扩充是数学内部发展的需要.
师:在自然数集中,方程x+1=0有解吗?
生7:没有解,在整数集中有解.
师:在整数集中,方程2x-1=0有解吗?
生8:没有解,在有理数集中有解.
师:在有理数集中,方程x2=2有解吗?
生9:没有解,在实数集中有解.
师:在实数集中,方程x2+1=0有解吗?
生10:在实数集中,方程x2+1=0无解,需要一个新的数集.
评析让学生从求解方程的需要,理解数系扩充的必要性,从而自然引入虚数单位i.
活动3 引入新数——虚数单位i.
师:我们需要引入一个数,使它是方程x2+ 1=0的解.如何引入?谈谈你的看法.
生11:可以引入虚数单位i,它的平方等于 -1,即i2=-1;它可以与实数进行四则运算,进行四则运算时,原有加、乘法运算律仍然成立.
师:把新引进的数i添加到实数集中,我们希望数i和实数之间仍然能像实数那样进行加法和乘法运算,并希望加法和乘法都满足交换律、结合律以及乘法对加法满足分配律.那么,实数集经过扩充后,得到新的数集由哪些数组成呢?
生12:形如a+bi(a,b∈R)的数组成新的数集.
评析数系经过扩充后要保证原来的运算律仍然成立,依据这个原则,新的数集的表达是一个很好的切入点.学生经过抽象过程认识到虚数单位,为实现复数概念的构建作铺垫,体现了数学概念教学中螺旋上升的思维过程,得出对象概念,实现认识上的飞跃.
3.3 建构概念、分析问题(对象阶段)
活动4 理解复数的概念.
师:形如a+bi(a,b∈R)的数,其中的a,b分别叫做什么?
生13:形如a+bi(a,b∈R)的数叫做复数,其中a叫做复数的实部,b叫做复数的虚部.
师:形如a+bi(a,b∈R)的数包括所有实数吗?它还包括哪些你原来没有遇到过的新数呢?
生14:包括所有实数,当b=0时,a+bi为实数;当b≠0时,a+bi为虚数,这是我们遇到的新数.
师:两个复数相等的条件是什么?对于a,b,c,d∈R,a+bi=c+di得满足什么条件?
生15:由a+bi=c+di得a=c,b=d.
评析通过以上问题促成学生对复数概念的准确理解;通过合作构建,为抽象出的复数概念赋予形式化的定义及符号表示,并让学生将复数主动纳入数系中.
活动5 类比实数集,认识复数集.
师:复数集C与实数集R之间有什么关系?
生16:每个实数都是虚部为0的复数,所以实数集R是复数集C的真子集.
师:依据复数a+bi中a,b的取值,如何给复数分类?
生17:对于复数a+bi(a,b∈R),当且仅当b=0时,复数a+bi是实数a;当b≠0时,复数z=a+bi叫做虚数;当a=0且b≠0时,z=bi叫做纯虚数;当且仅当a=b=0时,z就是实数0.
评析类比实数集,更清楚地认识复数集,感受数集的再次扩充.复数概念的抽象,其中虚数、纯虚数等概念容易混淆,细致的介绍说明可以帮助学生理解辨析,深刻理解复数的概念,有利于掌握复数的本质.将复数放在整个数系发展的历史长河中去认识,能够更加全面地认识复数概念,有利于下一阶段在头脑中更好地构建复数图式.
3.4 数学应用、解决问题(图式阶段)
例1已知(2x-1)+i=y-(3-y)i,其中x,y∈R,求x与y.
方法规律:若a,b,c,d∈R,则a+bi=c+di⟺a=c,b=d.特别地,a+bi=0⟺a=b=0.
评析通过复数相等的运用,将复数的运算转化为实部与实部、虚部与虚部的比较,实现了复数到实数的转化,渗透转化与化归的思想.
跟踪训练:(2x-1)i2+i=y-(3-y)i,其中x,y∈R,求x与y.
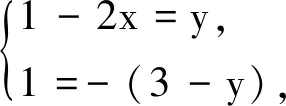
例2复数m=a+bi中实部a、虚部b满足什么条件时,复数z=m+1+(m-1)i是:
(1)实数?(2)虚数?(3)纯虚数?
师:因为m∈C,所以z=a+bi+1+(a+bi-1)i=(a+1-b)+(a+b-1)i是实数、虚数和纯虚数的条件可以确定m满足的条件.
生20:设m=a+bi,则z=a+bi+1+(a+bi-1)i=(a+1-b)+(a+b-1)i.(1)当a+b-1=0时,复数z是实数;(2)当a+b-1≠0时,复数z是虚数;(3)当a+1-b=0且a+b-1≠0时,复数z是纯虚数.
方法规律:在复数范围内解决问题,首先应设m=a+bi,再结合已知条件将相关复数也变成标准形式,进而将复数问题转化为实数的关系.
评析通过对实部和虚部的运算,加深对复数概念的理解和运用.设出复数也体现了方程思想,提升学生逻辑推理和数学运算素养.
变式训练:复数z=m+1+(m-1)i满足实部、虚部均大于1,求m的取值范围.
例3已知x∈C,求方程x2+x+4=0的根.

方法规律:一元二次方程的根在数集扩充后仍然可以用求根公式来求,这是数系扩充后仍然成立的结论.
评析在实际应用中体会引进虚数的必要性.随着数系的扩充对方程的解有了新的认识,这便是扩充数集的意义;求根公式仍然适用,这也是数集扩充的基本思想.
变式训练:x∈C,方程x2+x+4=0的两根为x1,x2,则x1+x2=-1,x1x2=4仍然成立吗?只说结论,不必证明.
师:既然求根公式仍然可用,即根与系数的 关系也仍然成立,故x1+x2=-1,x1x2=4成立.
评析通过例题讲解与变式训练,帮助学生记忆和构建复数概念形成的知识网络,有利于更好地形成概念图式.当然这个图式还需要在后续阶段反复学习,以不断完善、强化与稳固.
4 回顾与反思
(1)活动阶段:通过创设情境让学生亲身体验,发现问题,感受概念产生背景
“活动阶段”是概念引入阶段,以学生已有的认知结构为基础,通过创设情境提出问题,让学生参与各种“活动”主动构建,亲身体验、感受概念的直观背景和概念之间的关系.
在本节课的“活动阶段”环节中,以学生已有的自然数、整数、有理数、无理数、实数等概念知识为基础,认真分析复数概念的具体内容以及其在数系中的位置,通过创设情境提出问题,设计合适的“活动”,让学生参与各种“活动”主动构建,亲身体验、感受复数概念产生的直观背景和数系扩充的过程,了解引入复数的必要性,对于培养学生数学抽象的核心素养具有举足轻重的作用.在数系的扩充过程中体现了数学的发现和创造过程,也体现了数学发生、发展的客观需求,学生在活动阶段中通过学习复数的基本知识,体会人类理性思维在数系扩充中的作用.
(2)过程阶段:引导学生主动探究,提出问题,抽象出数学概念
“过程阶段”是概念定义阶段,应该是让学生对“活动”进行思考,通过一定的抽象得出概念所特有的性质,从而对所授的概念形成一个较直观的理解.
在本节课的“过程阶段”教学环节中,提出问题:“解方程时实数集不够用,怎么办?”有学生会回答:“把实数集扩充”.于是继续问:“你怎么想到的?怎么扩充?”接下来从方法论的角度启发学生:“我们遇到新的问题怎么解决?人类解决问题最本原的方法是什么?实际上我们通常是从已有方法寻找未知方法,从已有知识寻找未知知识,从已经解决的问题寻找解决新问题的方法!”接下来提问“你怎么想?”以引导学生找已知的知识和方法.找已经解决的问题.启发学生:有没有遇见过类似的问题?把问题交给学生,先思考后交流,不仅仅要让学生掌握复数的初步概念、定义、分类、相等的条件等知识,更重要的是理解复数这个数学概念建立的思想方法.
(3)对象阶段:让学生合作构建,分析问题,深化对概念的理解
“对象阶段”是概念分析阶段,应该是“活动”与“过程”的升华,将抽象出的概念赋予形式化的定义及符号表示,使其达到精致化,成为一个具体的“对象”,并由学生主动将其纳入已有的概念体系,在以后的学习中以此为对象进行新的活动.
在“对象阶段”环节中,教师给学生提供探究的线索,让学生通过合作构建来思考并分析问题:1)以往学习中有没有遇见过类似的问题?2)如果遇见过,解决了什么问题?怎样解决的?3)解决的过程有什么共同的特点(规律)?这些“线索”其实都是问题,而不是现成的线索;这些问题只提供了一个寻找线索的方法,真正的线索还需学生自己去寻找,而在寻找过程中所应用的类比思想和对方法论的认识无疑使学习中的“结果与过程”“客观与主观”“静态与动态”“外在与内化”有机地结合到了一起,积累了数学活动经验,为深入理解概念、提升数学素养奠定基础.
(4)图式阶段:进行概念的运用,解决问题,强化知识迁移形成智慧
“图式阶段”是概念运用阶段,是“对象”阶段中对概念本质和概念体系进一步理解,经过长期的学习揭示概念本质和实例化,与其他概念、规则、图形等建立起联系,在头脑中形成综合的心理图式.在“图式阶段”环节中,通过应用复数有关概念解决数学问题,让学生进一步理解复数概念以及它与已学过的实数概念的区别与联系,在头脑中建立起一定的概念图式,以便在解决问题时能够迅速调取.

