基于线性矩阵不等式的线性/非线性切换自抗扰控制系统的稳定性分析
万 慧, 齐晓慧, 李 杰
(陆军工程大学 无人机工程系,石家庄 050003)
韩京清[1]于1998年正式提出了自抗扰控制(Active Disturbance Rejection Control, ADRC).早期的自抗扰控制器为非线性结构,参数较多,整定相对困难,给理论分析带来了不便,因此发展较为缓慢.但仍有部分学者围绕扩张状态观测器(Extended State Observer, ESO)、参数整定以及控制器结构改进等方面进行了研究,如黄一等[2-3]通过自稳定域理论给出了低阶ESO的收敛性证明并对估计误差进行了研究,揭示了非光滑连续结构在控制器设计和误差观测中的优势.陈刚等[4]利用变结构控制原理对自抗扰控制器结构进行了改进,减少了需整定参数的个数.Zhao等[5]则针对一类非线性系统设计了时变增益ESO,进一步扩展了自抗扰控制器的应用范围.目前,这些成果仍具有很强的借鉴意义.Gao[6]提出了线性自抗扰控制器(Linear Active Disturbance Rejection Control, LADRC),该控制器物理意义明确,参数整定简单,为研究自抗扰控制理论带来了新思路.陈增强等[7]针对系统模型未知的情况,证明了线性扩张状态观测器估计误差有界和闭环控制系统输入-输出有界稳定.吴丹等[8-9]针对快速刀具伺服系统,分别设计了基于非线性自抗扰和线性自抗扰的控制器,从频域或准频域角度对自抗扰控制的稳定性和控制性能进行分析.邵星灵等[10]采用Lyapunov逆定理研究了任意扩张阶数下线性扩张状态观测器(Linear Extended State Observer, LESO)重构状态误差的收敛性问题,并对LESO及其高阶扩展形式的性能进行了评估分析,为ESO的选取提供了理论依据.周涛[11]利用反双曲正弦函数构造了一种新型自抗扰控制器,该控制器可以有效抑制系统内部和外部非线性扰动的影响,理论研究也促进了工程应用的进展.Sun等[12]引入极大值敏感函数用以对扩张状态观测器进行参数整定,并将其应用于1 000 MW机组的热力回热器,证明了ADRC在过程控制中具有较好的应用前景.张铁等[13]将LADRC应用于浮动平台的机器人研磨系统,减少了磨削过程中的力波动并降低了研磨表面的粗糙度.郭金龙等[14]则将改进的LADRC与分数阶控制结合,在四旋翼高度姿态控制中取得了良好效果,自抗扰控制逐渐成为国内外学者的研究热点之一.
目前,虽然LADRC是理论研究和工程应用的主流,但非线性自抗扰控制器(Nonlinear Active Disturbance Rejection Control, NLADRC)在稳态精度以及抗干扰能力等方面的潜在优势也不容忽视,在自抗扰控制体系的发展中,二者缺一不可.本团队为充分发挥二者优势,提出了综合两者优点的线性/非线性切换自抗扰控制(Linear/Nonlinear Switching Active Disturbance Rejection Control, SADRC)方法[15-16],在自抗扰控制研究领域引起了部分学者的关注.目前,针对单输入单输出(Single-Input Single-Output, SISO)被控对象,本团队已经完成了基于该方法的控制器设计和稳定性分析[15-16],并通过算例仿真的方式对该方法的抗干扰能力和跟踪精度进行了初步验证.除了本团队致力于研究 SADRC 相关内容外,刘福才等[17]将SADRC应用于变载荷气动加载系统中, 在工程实际应用中验证了SADRC具有良好的控制效果.朱熀秋等[18]采用SADRC实现了三自由度六极混合磁轴承解耦控制,并通过仿真和实验验证了该控制方法的有效性.郭杰等[19]针对欠驱动船舶航迹直线和曲线跟踪控制问题,设计了基于多模态快速非奇异终端滑模的自抗扰控制器,通过切换扩张状态观测器实现对船舶包含内扰和外扰的“总扰动”的实时估计.Yang等[20]针对船舶动力定位系统,提出了径向基-切换自抗扰控制器,克服了SADRC在切换临界点可能出现的抖振问题.Zhao等[21]针对四旋翼无人机的轨迹跟踪问题,设计了基于鲁棒微分器的切换自抗扰控制器,通过仿真验证了该控制器具有良好的抗白噪声能力.吴正平等[22]针对干扰弹滚转控制系统设计了切换自抗扰控制器,并用模糊规则改进了线性/非线性切换自抗扰控制条件,实现更为平稳的模糊软切换.虽然SADRC在工程应用研究方面取得了一定的成果,但是其理论分析仍进展较为缓慢,主要集中于对切换扩张状态观测器的收敛性分析[17, 23]和单输入单输出被控对象的稳定性分析[15].尽管有将其应用于多输入多输出被控对象的研究,但是只考虑了解耦后的单个子系统的稳定性[21],在理论上还有待进一步研究.
为进一步扩大SADRC的应用范围,本文针对一类连续线性多输入多输出标称系统进行基于 SADRC 的解耦控制器设计,并给出该系统闭环绝对稳定性以及考虑参数摄动情况下的鲁棒绝对稳定性分析方法.最后,通过数值仿真,针对不同的控制对象,对所提稳定性分析方法进行了验证.
1 多输入多输出系统的数学模型
考虑如下连续多输入多输出线性标称系统:

假设Cg可逆,引入虚拟控制量uv=[u1vu2v…umv]T∈Rm,则式(1)可整理为
(2)
式中:uv=Cgu=[u1vu2v…umv]T∈Rm.
2 基于SADRC的MIMO系统解耦控制方法
自抗扰控制技术的核心思想是利用扩张状态观测器消除系统中的未知项和扰动.为了提高扩张状态观测器的性能,使其适应更复杂的系统初始状态和干扰,本文设计的线性/非线性切换自抗扰控制器实际上是在线性扩张状态观测器和非线性扩张状态观测器之间进行切换,而鉴于线性控制律在实际应用中的优点,控制律仍采用线性控制律.
2.1 SADRC控制系统设计
为便于进行系统稳定性分析,做出如下假设.

以式(2)中x的第i(i=1, 2, …,m)个子系统为例,构造的切换扩张状态观测器(SESO)结构如下:
(3)
i=1, 2, …,m
式中:ei为每个子系统的输出yi及其对应估计值zi1之间的误差;zij(j=1, 2, …,n+1)为x的一个子系统中各状态xij的估计值,其中zi(n+1)为对该子系统总扰动的估计;βi0j为SESO中非线性扩张状态观测器(NLESO)的增益系数,并假设SESO中LESO的增益βi0jL是βi0j的λij倍,λij为常数;fij(ei)为切换函数,具体可表示为
(4)
式中:δsi为第i个子系统的控制器中NLESO与LESO进行切换的临界值,其取值可通过仿真、实验或理论计算确定[15],且在NLESO和SESO进行切换的过程中,当ei在临界点δsi时,观测器的增益是连续变化而不是突变的,虽然斜率有所变化,但不会带来严重的平稳性问题,故不会因为两种扩张状态观测器的切换造成系统不稳定;lij(ei)为NLESO中的非线性函数,本文采用的形式为
lij(ei)=fal(ei,αij,δi)=
(5)
式中:δi为每个子系统中控制器非线性函数中的线性段区间长度,大小根据实际情况确定;αij为常数,取αij<1时,则式(5)具有“小误差,大增益,大误差,小增益”的特性,当αij=1时,则式(5)变为线性函数.
(6)


j=1, 2, …,n+1


备注1为简化扩张状态观测器系统结构,此处各通道同阶的状态估计采用参数相同的切换函数,但实际上各通道同阶的状态估计所采用的切换函数参数可以不同.
各通道的控制律均采用线性控制律,可表达为
(7)
式中:viq(q=1, 2, …,n)为过渡过程;kiq(q=1, 2, …,n)为控制器增益;bi0=1为系统控制增益.
则控制输入uv可表达为
(8)
式中:
Kg=diag[kg1kg2…kgm] ,g=1, 2, …,n
根据假设1,将式(2)、(8)联立,可得:
(9)
式中:
将式(6)、(8)联立,可得:
(10)
式中:
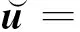
综合式(9)和(10),可得:
(11)
式中:

(12)
式中:
式(12)所示为输入多输出Lurie系统,可进一步表示为
(13)

2.2 SADRC控制系统稳定性分析

(14)
证明由于0<αij<1, 0<δij<δijs,∀ei≠0,故
(15)
进一步整理,可得
(16)
进一步可得
(17)

定理2若存在正定矩阵P∈R(2mn+m)×(2mn+m)和对角矩阵Λ=diag[r11r21…rm1…rij]≥0,Γ=diag[τ11τ21…τm1…τij]≥0(j=1, 2, …,n+1;i=1, 2, …,m),满足
W=
(18)
式中:G=diag[κ112-κ111κ212-κ211…κm(n+1)2-κm(n+1)1]=diag[κ11κ21…κm1…κij] (j=1, 2, …,n+1;i=1, 2, …,m)那么系统式(13)绝对稳定.
证明构造如下Lyapunov函数:
(19)
则有
(20)

式(14)等价于
(21)
j=1, 2, …,n+1;i=1, 2, …,m



(22)

(23)
式(23)等价于
W=
(24)
3 存在参数摄动的SADRC系统鲁棒稳定性分析
上文针对多输入多输出标称对象,研究了切换自抗扰控制系统的稳定性,但由于被控对象元件老化、工作环境变化等因素可能存在参数摄动情况,对系统的稳定性造成了直接影响,所以需进一步研究系统在参数摄动条件下的鲁棒稳定性分析问题.
实际系统中的参数摄动问题可用区间系统进行描述.在2.2节的研究背景下,因为只有矩阵A包含系统参数,故若被控对象存在参数摄动,则将连续线性输入多输出自抗扰控制系统转换为如下的输入多输出Lurie系统:
(25)
同时考虑如下系统:
(26)

3.1 基于端点矩阵法的SADRC系统鲁棒绝对稳定性分析

引理1对称区间矩阵L(P,Q)稳定的充要条件是其端点矩阵LV(P,Q)稳定.

(27)
式中:G=diag[κ11κ21…κm1…κij] (j=1, 2, …,n+1;i=1, 2, …,m),那么系统式(25)在式(14)约束下是鲁棒绝对稳定的.
证明构造Lyapunov函数:
(28)
则有

(29)

式(14)等价于
j=1, 2, …,n+1;i=1, 2, …,m
(30)



(31)

(32)
式(32)成立等价于

(33)
即证.
3.2 基于等价描述法的SADRC系统鲁棒绝对稳定性分析
采用端点矩阵法,在推算过程中,因为涉及对称区间矩阵的端点矩阵,故在计算线性矩阵不等式时相对繁杂.为降低计算的繁杂程度,采用等价描述法对SADRC系统的鲁棒绝对稳定性进行分析.
存在参数摄动的SADRC系统可转换为如下的输入多输出Lurie系统:
(34)
同时考虑如下系统:
(35)

引入区间矩阵的等价描述:

(36)
式中:
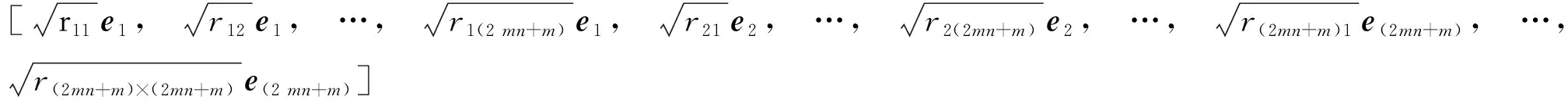

ei为(2mn+m)×(2mn+m)阶单位矩阵的第i个单位列向量.
证明考虑系统式(35)在约束条件式(14)下的绝对稳定性,构造Lyapunov函数:
(37)
式中:正定矩阵P∈R(2mn+m)×(2mn+m)和对角矩阵Λ=diag[r11r21…rm1…rij]≥0(j=1, 2, …,n+1;i=1, 2, …,m)为待定矩阵.
定义
(38)
则式(37)的导数为
(39)
式(14)等价于
j=1, 2, …,n+1;i=1, 2, …,m
(40)



(41)
并且由式(38)可得:
(42)
故可利用S-过程[24],如果存在Γ=diag[τ11τ21…τm1…τij]≥0(j=1, 2, …,n+1;i=1, 2, …,m),ε1>0,使得LMI
0
(43)
成立,则式(39)在式(14)的条件下是负定的,故有以下定理:
定理4如果式(43)的LMI存在P≥0,Γ≥0,Λ≥0以及ε1>0的可行解,那么系统式(34)在条件式(40)的约束下是鲁棒绝对稳定的.
4 数值仿真
考虑如下二阶输入多输出系统:
(44)
式中:y1、y2、ud1、ud2分别系统式(44)两个通道的输出和输入;K11=12.8,K12=-18.9,K21=6.6,K22=-19.4,在SADRC参数取值不变的条件下,为分析SADRC控制不同对象时控制系统的稳定性,验证SADRC控制器的控制性能,采用相同的SADRC控制器,对双积分串联型系统1、最小相位系统2、非最小相位系统3和4分别进行控制,不同被控对象的amn(m=1, 2;n=1, 2, 3, 4)取值如表1所示.

(45)

表1 不同系统模型参数取值Tab.1 Parameters of different system models
针对系统式(45)设计的SADRC控制器相关参数选择如表2所示,表中,wc为控制系统中控制器带宽;wo、woN分别为LESO和NLESO的带宽.

表2 SADRC控制器参数选择Tab.2 Parameters of SADRC controllers
4.1 稳定性分析
(1) 绝对稳定性分析.

(2) 基于端点矩阵法和等价描述法的鲁棒绝对稳定性分析.
4.2 仿真验证
(1) 绝对稳定性分析仿真实验.
基于MATLAB验证上述仿真结果.设置两通道初始值y1(0)=0,y2(0)=0,分别设置y1、y2通道期望值为yd1=1,yd2=1,并在仿真时间t=25 s 对y1、y2通道分别加入幅值为0.1和0.3的干扰,在保持SADRC参数情况不变的前提下,对表1中的4种被控对象进行控制,实验结果如图1所示.
由图1可以得出如下结论:① 在SADRC控制器参数选择适当的条件下,串联积分型系统、最小相位系统绝对稳定,系统具有较好的抗扰性,与理论分析结果一致;② 系统3对应的LMI虽然无解,系统不是绝对稳定的,但系统仍然可控,说明系统渐近稳定.这是因为求解LMI方法验证系统的稳定性是系统稳定性的充分条件,具有一定保守性,系统无法保证绝对稳定的情况下,仍可能是渐近稳定的,需要进一步进行判断;③不同被控对象在相同的SADRC控制器条件下,控制性能不同,串联积分型和最小相位系统的控制性能优于非最小相位系统和随机系统,说明被控对象的参数影响系统的控制性能;④ 根据被控对象的特点,可以发现,对于本文给出的线性标称输入多输出被控对象,被控系统本身稳定的,合理选择SADRC控制器参数,可以保证闭环系统绝对稳定,系统具有较好的控制性能,对于被控系统本身不稳定的,通过合理选择SADRC控制其参数,虽然无法保证系统绝对稳定,但系统仍可能是渐近稳定的.
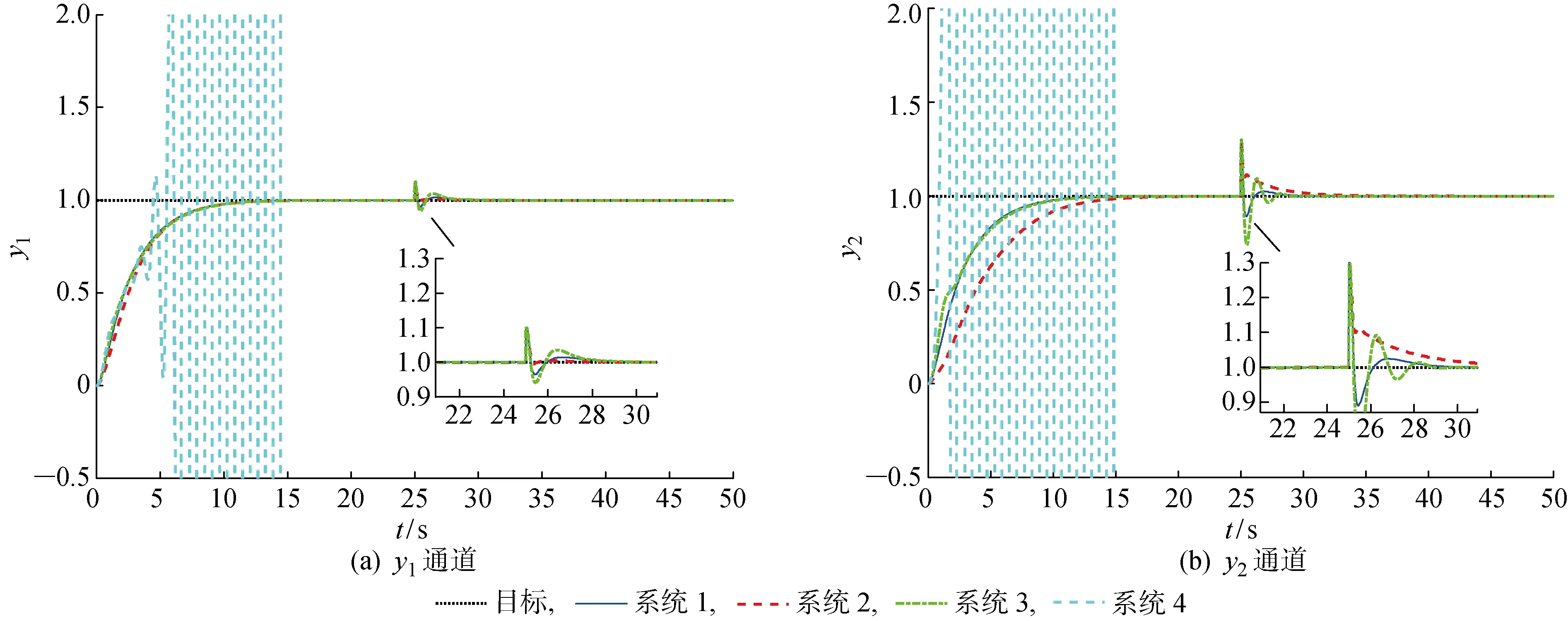
图1 被控对象两通道跟踪效果Fig.1 Tracking performance of two channels of controlled object
(2) 鲁棒绝对稳定性分析.
考虑模型参数amn(m=1, 2;n=1, 2, 3, 4)浮动值分别为±10%,±30%,实验条件设置同仿真实验(1),在参数浮动条件下两通道的跟踪效果分别如图2~5所示.
由实验结果可以得到如下结论:① 在控制器参数选择适当的条件下,串联积分型系统、最小相位系统是鲁棒绝对稳定的,且参数摄动对系统的控制性能影响不大,这是因为在系统鲁棒绝对稳定的条件下,与控制输入无关的参数变化可以视作系统的内部扰动,自抗扰控制可以对系统的内部扰动进行估计和补偿;② 系统3对应的LMI虽然无解,系统不是鲁棒绝对稳定的,但系统仍然可控,说明系统渐近稳定,在系统无法保证鲁棒绝对稳定的情况下,系统是否渐近稳定需要进一步验证;③ 对于不稳定系统4,参数摄动对系统的控制性能影响较大(见图3),当系统参数减小到一定程度,系统4的y1通道可控,而y2通道不可控,这说明当前控制器参数无法使系统4稳定,但是适当选择控制器参数,系统是可能稳定的.

图2 被控对象两通道跟踪效果(模型参数摄动-10%)Fig.2 Tracking performance of two channels of controlled object (-10% perturbation of model parameters)

图3 被控对象两通道跟踪效果(模型参数浮动+10%)Fig.3 Tracking performance of two channels of controlled object (+10% perturbation of model parameters)

图4 被控对象两通道跟踪效果(模型参数浮动-30%)Fig.4 Tracking performance of two channels of controlled object (-30% perturbation of model parameters)

图5 被控对象两通道跟踪效果(模型参数浮动+30%)Fig.5 Tracking performance of two channels of controlled object (+30% perturbation of model parameters)
5 结论
针对一类连续线性标称输入多输出控制系统,提出了基于SADRC的解耦控制方法,并针对该解耦控制系统给出了基于LMI方法的闭环控制系统绝对稳定性分析和鲁棒绝对稳定性分析方法 .同时采用数值仿真的方式,针对不同的被控对象对提出的绝对稳定性分析方法和鲁棒绝对稳定性分析方法进行验证,主要结论如下:
(1) 证明了在控制器参数选择适当的情况下,被控对象本身的特性(系统是否稳定、系统参数等)会影响闭环系统的绝对稳定性.
(2) 在闭环系统绝对稳定性无法保证的情况下,系统仍可能是渐近稳定的,这是因为LMI方法判断系统的绝对稳定性是充分条件,具有一定的保守性,在绝对稳定性无法保证的条件下,如何判断系统是否是渐近稳定的需要进一步研究.
(3) 在被控对象相同的情况下,与控制输入无关的参数摄动对系统的控制性能影响较小.需要指出的是,本文的研究对象进行稳定性分析时并未考虑外扰的影响,未来工作将考虑存在外扰情况下的MIMO系统稳定性分析.

