基于PF-UKF组合滤波的SINS/GPS组合导航系统空中对准方法

高红莲， 尤 杰， 曹松银

(扬州大学 信息工程学院，江苏 扬州 225127)

近年来，随着科学技术的飞速发展，导航技术也在不断进步.单一的导航系统已经难以满足现代复杂导航环境的需求，因此将多种导航系统进行组合已成为研究的热点[1].捷联式惯性导航系统(Strapdown Inertial Navigation System，SINS)和全球定位系统(Global Positioning System，GPS)的组合方式就是其中一种[2].SINS是一种利用惯性敏感器件测量运载体实时信息，并通过计算机进行解算得到运载体姿态、位置、速度等参数的导航技术[3]，具有稳定性强、刷新速率快、短时间精度高、可输出完整导航信息等特点.而GPS作为一种卫星导航系统，虽然其精度在短时间内与SINS存在一定差距，但不会随着时间累积误差，并且能在全天候、全时段以及全球范围内提供精准的导航信息[4].由此可见，两种导航系统能够取长补短，弥补各自不足.一方面，GPS具有误差不随时间积累的特点，通过GPS的测量信息能够实时对SINS的误差进行校正，解决SINS误差随时间累积的问题[5].另一方面，利用SINS的高稳定性、高动态性等特点可以克服GPS信号易受遮挡、周跳等问题，两者的结合能有效降低单一导航系统的局限性[6].

对于SINS/GPS组合导航系统，滤波算法是关键技术之一.滤波算法将SINS解算后的数据与GPS数据进行融合，以此修正导航系统的误差，大大提高了导航性能[7].针对含有多源干扰的惯性导航系统，文献[8]提出了一种基于鲁棒多目标滤波器的线性初始对准方法，采用漂移估计器估计惯性传感器误差，混合H2/H∞滤波器抑制高斯噪声和范数有界干扰.针对空间噪声的不确定性导致卡尔曼滤波性能降低的问题，文献[9]设计了一种基于扩展H∞滤波的鲁棒滤波算法来实现多传感器信息融合.针对非高斯噪声，通过最大相关熵和残差正交原理构造相关代价函数，文献[10]提出了一种基于自适应信息熵理论的鲁棒容积卡尔曼滤波器.针对导航系统存在的非线性动力学、器件漂移、参数不确定性等多源干扰，文献[11]提出了一种基于干扰抵消和抑制的多目标滤波方法，并用于惯导系统非线性初始对准问题.针对系统噪声不确定性对无迹卡尔曼滤波(Unscented Kalman Filter，UKF)性能造成的影响，文献[12]提出了一种基于最大似然原理的自适应UKF算法来估计过程噪声的协方差.此外，粒子滤波(Particle Filter，PF)由于其适用于非高斯、非线性的情形，已广泛应用于组合导航系统.但是，随着时间增加，PF的重要性权值可能会集中到少数粒子上，出现粒子退化现象[13].粒子退化会造成计算量都浪费在无用粒子上，降低算法效率，甚至导致滤波发散.

当前，许多SINS/GPS组合导航系统考虑小姿态误差角下的线性误差模型，当运载体处于大失准角运动状态时，该系统模型具有一定的模型误差[14].因此，针对UKF和PF等滤波方法的不足以及运载体处于大失准角下的情况，本文提出一种基于误差四元数模型的PF-UKF组合滤波算法.摒弃传统的小失准系统误差方程，利用误差四元数代替状态向量中的3个失准角，使得系统模型能够在大失准角状态下保持相对精准度.此外，结合UKF和PF两种滤波算法的优点，将采样粒子分为由概率密度函数采集的随机粒子和由UKF采集Sigma点求取后的状态值构成的确定粒子，不仅能够克服UKF对噪声统计特性的约束，同时能有效降低PF存在的粒子退化问题.仿真结果表明：与PF相比，所提出的滤波算法具有更好的滤波精度，并当系统存在非高斯噪声和干扰时，具有很好的抗干扰能力.

1 SINS/GPS组合导航系统误差模型

1.1 状态方程

利用误差四元数建立新的系统误差模型，状态方程由SINS的误差模型来表示.设导航坐标系为东(E)、北(N)、天(U)坐标系.16维的系统状态向量如下：

建立SINS/GPS组合导航系统的非线性状态方程为

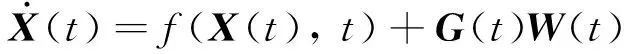
(1)

式中：t为系统连续状态的时间；f(X(t),t)为系统非线性函数；G(t)为系统噪声驱动矩阵；W(t)为系统噪声，且

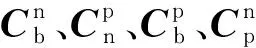
1.2 量测方程

将SINS位置和GPS接收机输出位置的差值以及SINS速度和GPS接收机输出速度的差值作为量测信息，建立量测方程：

(2)

(3)

式中：h(X(t),t)为非线性部分；λI、LI、hI为SINS位置输出值；λG、LG、hG为GPS位置输出值；vIE、vIN、vIU为SINS速度输出值；vGE、vGN、vGU为GPS速度输出值；δλI、δLI、δhI为SINS位置误差；δvGE、δvGN、δvGU为GPS速度误差；V(t)为量测噪声.

对系统(1)和(2)离散化，得到SINS/GPS组合导航系统的离散非线性误差模型为

XK+1=f(XK)+WK

(4)

ZK=h(XK)+VK

(5)

式中：下标K表示时刻.与UKF相比，并不默认WK和VK两种噪声为独立的白噪声，不规定噪声类型.

2 PF-UKF组合滤波器设计

结合PF和UKF算法，将采样粒子分为两部分进行采集，降低了粒子退化的程度，具体过程如下.

(1) 初始化.由先验状态分布抽取初始值X0，确定初始状态矢量和初始协方差：

(6)

(7)

式中：E(·)为期望函数.

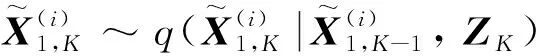
计算2r+1个Sigma点和权值：

(8)

(9)

(10)

W0=τ/(r+τ)

(11)

Wi=1/[2(r+τ)]

(12)

Wi+r=1/[2(r+τ)]

(13)

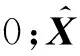
Xi, K/K-1=f(Xi, K-1)

(14)

(15)

状态一步预测均方差为

(16)

Zi, K/K-1=h(Zi, K/K-1)

(17)

(18)

(19)

(20)

式中：RK为K时刻的量测噪声.

滤波器增益值为

(21)

更新系统状态变量估计值为

(22)

状态变量估计均方差方程为

(23)

式中：PK为后验协方差.

(24)

式中：q(·)为重要性概率密度函数；N(·)为正态分布.

(4) 将得到的随机粒子和确定粒子统一进行权值计算，对其进行权值归一化：

(25)

(26)

式中：P(·)为后验概率分布函数.

(5) 为了使所采集的随机粒子和确定粒子的数量能够保证规定的有效粒子数，在不满足时仍对其进行重采样步骤，使得有效粒子的权值为1/N，此时计算状态估值：

(27)

3 实验仿真结果及分析

3.1 仿真条件

为了验证SINS/GPS组合导航系统下的PF-UKF组合滤波器的性能，将其与传统的PF算法进行仿真对比.设置初始条件如下：初始位置为东经40°、北纬50°、高800 m，SINS初始速度误差为 0.1 m/s，东、北、天3向失准角误差为1°、1°、5°，加速度计初始偏差为1×10-4g，加速度计随机偏差为5×10-5g，陀螺仪常值漂移为0.05(°)/h，陀螺仪随机漂移为0.1(°)/h，惯性器件采样时间为0.05 s.GPS的速度误差为0.1 m/s，水平位置误差为2.5 m，高度位置误差为5 m，GPS信号采样周期为0.1 s.考虑大失准角下的运载体状态，采用四旋翼无人机设备进行数据采集，如图1所示.其飞行轨迹设置为从初始位置起匀速直行50 s, 左转90° 匀速飞行50 s，右转45° 匀速飞行50 s，爬升20° 匀速飞行100 s，下降20° 匀速飞行100 s.

图1 四旋翼无人机Fig.1 Quadrotor UAV

3.2 结果与分析

对PF算法和PF-UKF组合滤波算法下的位置误差和速度误差进行对比.图2分别为在PF以及PF-UKF下的经度、纬度和高度位置误差，图3分别为在PF以及PF-UKF下的东、北、天3向的速度误差；表1为两种方法下的速度误差和位置误差的标准差.

图2 不同算法下的位置误差Fig.2 Position errors of different algorithms

图3 不同算法下的速度误差Fig.3 Velocity errors of different algorithms

表1 PF和PF-UKF下的速度误差和位置误差标准差Tab.1 Standard deviations of velocity error and position error based on PF and PF-UKF

图2中，虽然PF和PF-UKF都能使系统速度误差趋于稳定状态，但PF下的位置误差的波动明显大于PF-UKF，并且PF-UKF下的位置误差收敛速度更快，精度也更高.图3中，虽然PF和PF-UKF下的速度误差在开始阶段都存在一定的波动性，但PF-UKF算法下的速度误差收敛速度更快，大约在50 s后逐渐收敛，并趋于平稳.由表1可知，相比于PF，PF-UKF滤波下的位置误差和速度误差标准差均较小，说明该滤波器更加稳定.无论是位置误差还是速度误差，导航系统的误差在PF-UKF滤波下得到了更有效的收敛，并且相比于传统的PF滤波，所提滤波算法在大失准角的状态下，效果也更优异，有效克服了传统PF滤波存在的粒子退化问题，降低了粒子退化程度.由此可见，在PF-UKF滤波下，SINS/GPS组合导航系统能够在大失准角的状态下获得了较好的滤波效果，有效提高了系统的导航精度和收敛速度.

4 结语

传统的SINS/GPS组合导航系统误差模型主要应用于小失准角的情况，但实际上运载体常处于大失准角的状态，且系统噪声特性未知.而传统PF又存在粒子退化问题，本文将PF算法和UKF算法相结合，提出了一种基于PF-UKF的组合滤波算法.利用误差四元数代替状态向量中的3个姿态角，使得系统模型能够在大失准角的状态下保持相对精准度.此外，为了降低传统PF算法中粒子退化的程度，将PF-UKF滤波算法所要处理的粒子分为由UKF采集Sigma点后求取的状态值构成的确定粒子和由PF的概率密度函数采集的随机粒子.结果表明：该滤波算法不仅能够克服UKF对噪声要求的问题，同时能够有效克服PF存在的粒子退化的问题，具有较好的鲁棒性.