深空探测器接近段自主导航的滑动窗口自适应滤波方法

张文佳， 马 辛

(北京航空航天大学 仪器科学与光电工程学院，北京 100091)

深空探测器在着陆目标行星之前将经历巡航段、接近段、环绕轨道段.与相对稳定的巡航和环绕轨道段相比，接近段至关重要，决定了航天器能否进入围绕目标行星的预定轨道[1-2].导航系统作为深空探测任务的重要组成部分，直接影响深空探测器的运行状态[3].一般来说，在接近段，导航系统的位置精度为1～10 km，而每次轨道确定所需的无线电测量和延迟时间为10～100 min.因此，深空探测器导航系统的精度和实时性是保证深空探测任务成功的两个重要因素.

天文导航是深空中使用的主要自主导航方法之一，包括水手号和旅行者号在内的航天器都使用天文导航.深空探测器的自主导航系统一般由轨道动力学、量测模型和最优状态估计方法组成.滤波方法对导航系统的性能至关重要，它决定了参数估计的准确性和实时性.为获得深空探测器的位置和速度，模型加速度通过数值积分器融合到滤波器中，通常采用具有固定步长的四阶龙格库塔积分法[4-5].

对于深空探测器而言，在接近阶段探测器会遇到快速时变的误差问题.这是目标星体的引力影响急剧增加，而其他天体的引力影响相对稳定所导致的.由于深空探测器目标星体的引力快速变化，所以滤波器中的数值积分误差会给导航性能带来额外的不确定性，这被视为系统模型误差，并且难以确定其统计特性.

对于无法准确估计噪声的问题，很多学者进行了研究并提出3类解决方法[6-8]：基于协方差估计的滤波方法、方差匹配方法和多模型自适应方法.Fang等[6]提出一种基于新息的自适应扩展卡尔曼滤波方法，以提高全球定位系统的对准精度.Ning等[7]根据新息序列和残差序列的变化，提出一种具有自适应测量噪声协方差的无迹卡尔曼滤波器(Unscented Kalman Filter, UKF).Xiong等[9]提出一种多模型自适应估计方法，用于未知系统噪声统计特性和测量不确定度的系统.然而，这种方法很难防止滤波器发散，更换状态模型会导致精度降低.Liu等[10]使用模糊自适应无迹卡尔曼滤波解决车辆惯性导航的问题.Gao等[11]提出基于强化学习的自适应卡尔曼滤波方法.Fraser等[12]提出基于残差的模糊自适应扩展卡尔曼滤波方法.卞鸿巍等[13]使用基于新息的卡尔曼滤波算法提高了舰用组合系统的性能.Huang等[14]在惯性/卫星组合导航中使用变分自适应卡尔曼滤波算法.Zhang等[15]使用多模态变分自适应卡尔曼滤波船舶组合导航系统的量测噪声.这种方法设计的滤波系统复杂，计算量较大.此外，Zhang等[16]使用一种非线性优化方法解决了复杂环境下移动机器人的自主导航问题.

针对深空探测器接近段无法准确估计状态噪声和现有滤波方法计算量大以及难以防止滤波器发散的问题，提出一种基于系统噪声协方差调整的滑动窗口自适应无迹卡尔曼滤波方法(Sliding Window Adaptive Unscented Kalman Filter Based on System Noise Covariance Adjustment, AQUKF)，通过将前一时刻系统噪声协方差与噪声协方差的变化进行加权，提高导航系统性能.

1 问题描述

1.1 轨道动力学模型

深空探测器在接近目标行星时沿双曲线轨道移动，其中心天体是目标行星，太阳和其他行星被认为是扰动.此外，太阳光压辐射和推进器脉冲等因素也会影响探测器的运动.考虑以上因素，以火星为目标天体，火心惯性坐标系统中的轨道动力学方程可描述如下[7]：

(1)

设状态矢量X=[xyzvxvyvz]T，f(·)为过程函数，W为过程噪声，式(1)可写为

(2)

1.2 星光角距量测模型

背景恒星和火星、火卫一、火卫二之间的星光角距可作为量测量[17].如图1所示，本文使用行星敏感器得出恒星与目标行星之间的角度.图中：θpi,θdi分别为第i颗恒星与火卫一、火卫二之间的角度；lpp,lpd分别为火卫一、火卫二到探测器的视线矢量；spi为第i颗恒星在火卫一传感器视场的矢量.

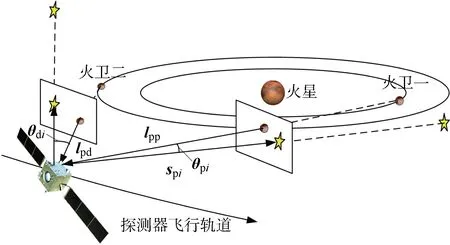
图1 恒星和导航天体之间的角度Fig.1 Angle between the star and Mars

在火星探测器导航系统中，星光角距量测模型可以表示为

(3)

式中：i=1, 2, 3；θmi为第i颗恒星与火星之间的角度；lpm为火星到探测器的视线矢量；smi,sdi分别为第i颗恒星在火星、火卫二传感器视场的矢量；vm,vp,vd分别为第i颗恒星与火星、火卫一、火卫二之间的量测噪声.

设量测矢量Z=[θmiθpiθdi]T，h(·)为量测模型函数，V为量测噪声，式(3)可写为

Z(t)=h(X(t),t)+V(t)

(4)

1.3 不确定性误差及其传递特性

1.3.1积分误差分析 无论何种数值积分方法，都是轨道动力学微分方程的近似解，因此会产生计算误差.由于计算过程可以等效于前后两步之间斜率的加权平均值与积分步长的乘积，所以斜率的加权平均值会产生较大的近似误差(即非线性微分方程误差的截断).积分步长越小，近似误差越小.因此，积分误差主要受数值积分步长的影响.另外，由数值积分方法引起的摄动加速度误差可以表示为

(5)

1.3.2积分误差传递分析 轨道动力学模型积分误差传播模型可以表示为

(6)

式中：t1和t2分别为起、止时间.

在接近阶段结束时，四阶数值积分的误差为

(7)

以中心天体重力加速度为例可得：

(8)

如式(6)所示，轨道动力学模型的积分误差随积分步长而变化.当轨道高度为距火星200 km、积分步长为250 s时，轨道动力学模型引起的加速度误差约为 0.002 1 m/s2.刹车后，继续飞行约10 min，速度误差约为1.26 m/s，位置误差为750 m.因此，积分误差会影响导航精度，尤其是在接近阶段.

当航天器遇到目标天体时，目标天体会导致航天器加速度急剧增加.如果积分时间步长较大，则无法快速跟踪加速度的变化，会引入较大的积分误差.因此，状态模型的误差在接近段急剧增加，过程噪声在航天器接近目标时无法保持不变.为准确估计航天器的位置和速度，需要采用自适应非线性滤波估计过程噪声协方差.一方面，为保证导航精度，需要减小状态模型误差；另一方面，为获得更好的导航性能，应该跟踪或估计状态模型的变化.

2 自适应无迹卡尔曼滤波

2.1 传统无迹卡尔曼滤波

非线性离散随机系统在特定时刻k的状态模型考虑如下：

(9)

式中：Xk和Zk分别为k时刻的状态矢量和观测矢量；wk和vk分别为k时刻的过程噪声和量测噪声.假设量测噪声和过程噪声是具有可加性的零均值高斯白噪声且互不相关，则

(10)

式中：Qk和Rk分别为k时刻的过程噪声协方差和量测噪声协方差；当k=j时，克罗内克函数δkj取值为1，当k≠j时，δkj取值为0.

对于具有可加性噪声的非线性系统式(9)，传统的UKF计算过程如下.

步骤1设定滤波初值.当k=0，有

(11)

式中：P0为协方差矩阵P的初始值.

步骤2计算k-1时刻的Sigma点：

(12)

步骤3计算k时刻的一步预测值.首先根据非线性函数f(·)，计算Sigma点的变换结果：

(13)

然后计算出一步预测结果和对应的协方差矩阵：

(14)

Qk-1

(15)

步骤4计算k时刻的一步预测Sigma样本点：

(16)

步骤5计算一步预测量测值及其自协方差矩阵、互协方差矩阵.根据非线性函数h(·)，量测Sigma样本点的变换为

(17)

那么一步预测量测值为

(18)

自协方差矩阵为

(19)

与一步预测状态量之间的协方差矩阵为

(20)

步骤6计算卡尔曼增益、状态估计结果及其协方差矩阵：

(21)

(22)

(23)

步骤7对k+1重复执行步骤2～6.

对步骤2～6的参数设置如下：

(24)

λ=α2(n+τ)-n

(25)

式中：α为很小的正数；β为X的分布信息；参数τ常取τ=3-n，故式(25)又可以写为

λ=3α2-n

(26)

2.2 自适应协方差调整的UKF

(27)

(28)

因此，使用宽度为N的滑动窗口对式(28)进行平稳化处理：

(29)

如果

(30)

令

(31)

式中：T为滤波周期.

那么，可以重新得到状态噪声估计：

(32)

3 仿真和分析

3.1 仿真参数设置

以火星探测器为例进行仿真分析，仿真数据由系统工具包产生.坐标系采用J2000.0火心惯性坐标系，轨迹参数如表1所示.表中：a′为长半轴；e为偏心率；i′为轨道倾角.

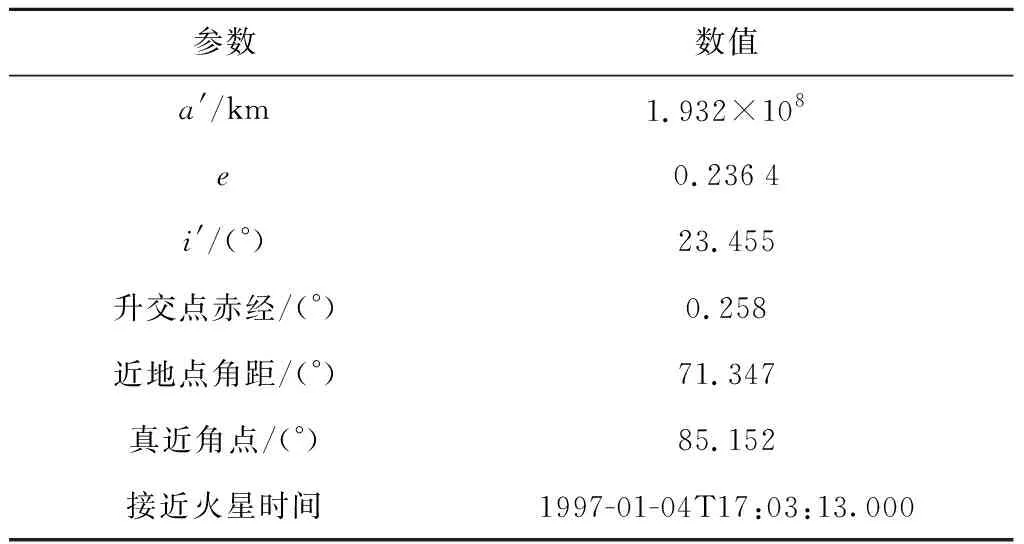
表1 火星探测器轨道参数Tab.1 Orbit parameters of Mars probe

参考轨道由RKF89数字积分器生成，该积分器使用1 s的固定步长，时间为1997年7月1日0时0分0秒至1997年7月8日0时0分0秒.在接近段，火星和探测器之间的最小距离为 5 211 km.仿真中使用的行星星历和恒星数据库分别是JPL DE421星表和第谷恒星星表.量测中的导航天体为火星、火卫一和火卫二.火星、火卫一、火卫二和恒星传感器的精度设置为0.1像素，火星、火卫一和火卫二的光学传感器参数如表2所示.表中：f′ 为焦距；

表2 光学传感器的参数Tab.2 Parameters of optical sensor

FOV为视场角；R为分辨率.

滤波器的初始参数设置如下.

初始状态为

X0=[rv]=

[1.590 5×1096.504 4×1082.829 5×107

-4.925×103-2.030 5×10376.742 2]

初始状态协方差为

P0=diag(106, 106, 106, 102, 102, 102)

初始状态噪声协方差为

Q0=diag(10-3, 10-3, 10-3, 10-8, 10-8, 10-8)

初始量测协方差为

R=

窗口宽度N设置为10.

3.2 结果分析

分别使用UKF和扩展卡尔曼滤波方法对非线性模型式(9)进行滤波，然后与AQUKF进行比较分析，最后对AQUKF方法进行影响因素分析.

3.2.1UKF与AQUKF滤波方法的结果比较 图2和图3分别给出了使用UKF和AQUKF方法的滤波结果.仿真结果的统计时间段从第1天开始

图2 UKF方法滤波结果Fig.2 Results of UKF algorithm

图3 AQUKF方法滤波结果Fig.3 Results of AQUKF algorithm

至结束.图2中：Dr=‖Dr‖=‖[DxDyDz]>‖为航天器位置的误差；Dv=‖Dv‖=‖[DvxDvyDvz]>‖为航天器速度的误差.

表3给出了UKF和AQUKF方法滤波收敛后的平均误差和最大误差.由表3可知，本文提出的AQUKF方法位置精度比UKF提高90.97%；速度精度比UKF提高66.17%.从图2(a)可以看出，探测器在第3天末x方向和y方向的位置误差出现较

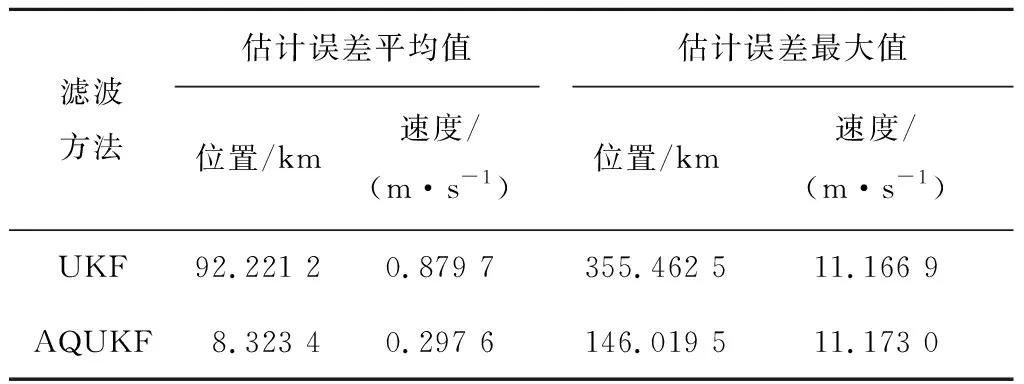
表3 UKF和AQUKF滤波方法的结果Tab.3 Results of UKF and AQUKF filtering methods

大发散，并且直到第7天也没有收敛回来；从图2(b)可以看出，探测器在第3天末x方向和y方向的速度误差同样出现较大发散.与位置误差发散不同的是，速度误差在发散后出现短暂收敛，并在一个恒定误差上下波动.从图3可以看出，本文提出的AQUKF有效抑制了UKF带来的发散问题，提高了导航系统的稳定性和精度.

图4为UKF与AQUKF位置误差和速度误差对比.从图中可以清楚地看出，在约3.7 d时，UKF滤波位置误差和速度误差开始发散.从图4(b)中可以看出，3.7 d时AQUKF出现的尖峰比UKF稍大一些，约增加1.37 m/s，但是AQUKF可以在1.5 h内恢复收敛，而UKF并未恢复收敛.这说明探测器在某一时刻受到干扰时，利用AQUKF滤波可以很快恢复收敛，提高了导航系统的稳定性.另外从图4(b)可以看出，AQUKF在恢复收敛之后速度误差仍然很小.

图4 UKF与AQUKF估计误差对比Fig.4 Comparison of estimation error between UKF algorithm and AQUKF algorithm

3.2.2影响因素分析 对基于AQUKF的火星探测器导航方法在不同影响因素下的滤波性能进行仿真分析，包括滤波周期、窗口大小.其余仿真条件与3.1节保持一致.

(1) 滤波周期对导航方法精度的影响.

表4和图5给出了窗口大小为10、不同滤波周期时的滤波结果.根据图表可知滤波周期越短导航系统性能越好，随着滤波周期减小，精度提升速度变慢，因此调整滤波周期的大小对导航滤波精度的提高是有限的.当滤波周期较长时，导航滤波结果所受影响较大，原因是系统轨道动力学模型的线性化误差随时间积分进一步增大，致使系统的性能下降.当采样周期大于600 s时，估计误差曲线波动幅度变大，特别是在接近火星时位置和速度均出现较大误差，导航性能较差.

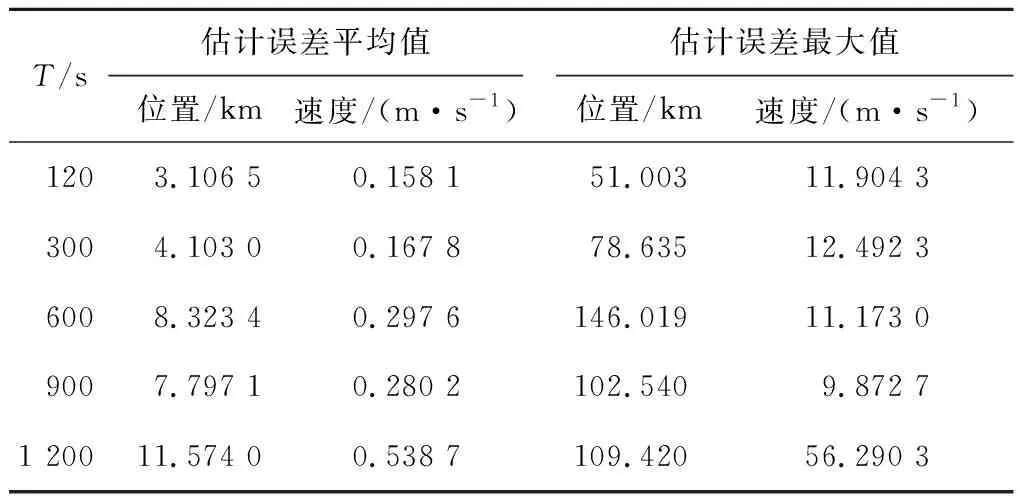
表4 滤波周期对导航方法精度的影响

(2) 窗口大小对导航方法精度的影响.

图6和表5给出了滤波周期为600 s、不同窗口大小时的滤波结果.根据图表可知，窗口较大或者较小时导航系统性能均有所下降.当N<10，在探测器靠近火星时会利用更多当前时刻的信息去自适应过程噪声协方差，这样就会导致导航系统性能在该时刻附近突然降低，进而影响整个时间段的系统性能.而随着时间的增加，误差也会累积增加，因此当N>10时，在利用较多历史信息的同时，也导致误差的累积.当N=10时，平衡了当前时刻和历史时刻信息带来的误差，导航性能相对最佳.

图5 滤波周期对位置误差和速度误差的影响Fig.5 Influence of filtering period on position error and velocity error

图6 窗口大小对位置误差和速度误差的影响Fig.6 Influence of window size on position error and velocity error

表5 窗口大小对导航方法精度的影响

4 结语

本文提出一种深空探测器自主天文导航的滑动窗口自适应UKF方法，即AQUKF，相比于使用传统UKF的算法，AQUKF算法通过自适应调节系统噪声协方差，不仅解决系统发散问题，提高系统的稳定性，还可以大幅提高导航精度.由于AQUKF对窗口大小的敏感程度较小，所以不需要为选择合适的窗口消耗更多时间，也不需要通过优化目标方程选择窗口大小，损失系统的实时性.该方法可为我国未来深空探测器任务自主导航系统的研制提供参考.