基于累积前景理论和三支决策的无人机态势评估
李伟湋, 高培雪, 陈 进, 路玉卿
(南京航空航天大学 a. 航天学院; b. 计算机科学与技术学院/人工智能学院/软件学院; c. 高安全系统的软件开发与验证技术工信部重点实验室,南京 210016)
随着科技发展,无人机作战成为现代战争中不可或缺的一环,已逐步应用于战争中的侦查、评估和监听等各个方面.无人机态势评估是指评估敌我双方的战斗力要素,对整体战场态势进行判断,帮助飞行员做出正确决策.对敌机态势进行合理评估是进行火力分配和机动决策的前提,在战争中发挥着关键作用.在评估过程中,无人机本身动力较小,容易受天气、地形等环境因素影响.同时,无人机控制系统难以自主处理飞行过程中的突发事件[1].因此,深入研究无人机态势评估刻不容缓.
近年来,众多学者对无人机态势评估展开研究,提出了多种态势评估方法.较为常见的有以下几种:文献[2]提出了一种基于贝叶斯网络的态势评估方法;文献[3]构建云模型得到目标威胁评估云图,实现了威胁评估;文献[4]为了提高空战中目标威胁评估模型的精度,构建极限学习机来解决态势评估问题.无人机态势评估是信息融合的过程,将多种低层次的信息融合为高层次的信息,从而对目标进行态势评估,得到威胁排序结果.因此,在一些研究中,将无人机态势评估视为一种群体决策[5]或多属性决策[6]的问题.由于作战环境日趋复杂,且无人机容易受到环境影响,导致态势信息具有明显的不确定性和模糊性.为解决该问题,文献[6]用直觉模糊集来处理信息的不确定性,使用隶属度函数精确地描述了不确定信息,将其用于评估空中目标威胁程度.文献[7]采用直觉模糊熵计算目标属性权重,引入直觉模糊多准则妥协解排序(VIKOR)方法用以解决多目标威胁评估问题.文献[5]将群体决策模型应用到目标威胁评估上,之后,文献[8]针对目标威胁评估只能得到威胁排序需要进一步研究是否应该攻击目标的问题,在直觉模糊环境下提出了一种基于三支决策的目标威胁评估算法.同时,文献[9]将前景理论引入到决策问题中,文献[10]将前景理论运用到空战目标威胁评估中,文献[11]进而提出一种基于前景理论和VIKOR法的威胁评估方法.
但当前的无人机态势评估过程仍然存在以下两个问题:其一,当前多数的态势评估方法只能得到评估的排序结果,仍需飞行员主观地选择优先攻击的目标和数量,并且飞行员在决策过程中多为二支决策,即判断是否对敌机进行攻击,对于中等威胁的目标,需要更多的信息进行判断,评估过程复杂,容易出现误判,易导致决策错误;其二,外界的复杂环境会影响飞行员的个人偏好,不同的飞行员心理偏好不同,在整个空战过程中,同一飞行员的心理倾向也会发生变化,而以往的评估过程中没有考虑决策者的主观偏好和风险态度,不能反映出真实的作战场景.
针对上述问题,提出一种基于三支决策和累积前景价值理论的态势评估方法.首先利用三支决策模型进行态势评估,该模型在传统决策问题的基础上,为不确定性结果增加了延迟决策的选择,更加符合人的决策认知;然后引入累积前景理论体现飞行员偏好的不确定性,在此过程中使用记分函数将直觉模糊数转换为实数,从而计算指标平均值,利用指标平均值和正负理想点得到参考点;为建立基于累积前景理论的三支决策模型,根据损失和结果之间的数量关系,得到对应的结果矩阵,之后通过比较一个目标的3种累积前景价值进行快速决策.此外,为了考虑不同类型飞行员面对相同战场态势时的区别,得出与实战情景相符的评估结果,对3种类型的飞行员进行实验,得到不同的评估结果.
1 相关理论
1.1 直觉模糊集
设U是一个非空论域,则U上的一个直觉模糊集可以表示为:A′={〈x,μA(x),vA(x)〉|x∈U},其中,μA(x)为论域中的元素x属于A′的隶属度;vA(x)为元素x属于A′的非隶属度.μA(x):U→[0, 1]和vA(x):U→[0, 1]是论域上的两个映射,对∀x∈U,需满足以下3个条件:μA(x)∈[0, 1],vA(x)∈[0, 1]以及μA(x)+vA(x)∈[0,1].定义πA(x)=1-μA(x)-vA(x)为直觉模糊集A′的犹豫度.
直觉模糊集中的元素被称为直觉模糊数.设E=(μE,vE)和F=(μF,vF)是两个直觉模糊数,与直觉模糊集的定义类似,μE、vE和πE分别为直觉模糊数E的隶属度、非隶属度和犹豫度,μF、vF和πF分别为直觉模糊数F的隶属度、非隶属度和犹豫度;其中,πE=1-μE-vE,πF=1-μF-vF.常见运算为
|πE-πF|)
(1)
S(E)=μE-vE
(2)
式中:d(E,F)为距离函数,用于计算两个直觉模糊数之间的距离;S(E)为记分函数.
1.2 三支决策
三支决策理论的基本思想是在实体评价函数上引入两个阈值,并构造所需的3个域,分别为正域、负域和边界域,这3个域可以分别解释为接受、拒绝和不承诺.根据贝叶斯决策过程,决策粗糙集由2个状态和3种行动组成[12], 构造状态集和动作集,状态集Ω={C,C}表示对象属于集合C和不属于集合C,动作集AC={aP,aB,aN},aP、aB和aN分别表示接受、进一步研究和拒绝动作,下标P、B和N分别为对象x采取接受、进一步研究和拒绝动作.不同状态下执行不同的动作会存在不同的损失,对应的损失函数矩阵如表1所示.其中,λPP、λBP和λNP分别为在状态C中的对象采取接受、进一步研究和拒绝动作时的损失;λPN、λBN和λNN分别为不在状态C中的对象采取接受、进一步研究和拒绝动作时的损失.同时,存在一个合理的损失函数条件:λPP≤λBP≤λNP,λNN≤λBN≤λPN.

表1 损失函数矩阵Tab.1 Loss function matrix
对于某一个对象x,其在状态C中的概率为P(C|x),又称为条件概率,根据条件概率大小可得到决策排序结果.对象x执行不同的动作有不同的期望损失,如R(aP|x)为对象采取接受动作时的期望损失;R(aB|x)为对象采取进一步研究动作时的期望损失,R(aN|x)为对象采取拒绝动作时的期望损失.通过比较其执行不同动作时的期望损失将对象划分到正域、边界域和负域中,分别用POS(C)、BND(C)和NEG(C)表示.由此可得决策规则(P)、(B)、(N)如下:
(P)如果R(aP|x)≤R(aB|x)和R(aP|x)≤R(aN|x),则x∈POS(C).
(B)如果R(aB|x)≤R(aP|x)和R(aB|x)≤R(aN|x),则x∈BND(C).
(N)如果R(aN|x)≤R(aB|x)和R(aN|x)≤R(aP|x),则x∈NEG(C).
1.3 改进累积前景理论
1.3.1累积前景理论 Tversky等[13]提出了累积前景理论,其核心为累积前景价值,它由累积权重函数和价值函数两部分组成,假设共有a1+a2+1个结果,记为x=x-a1,x-a1+1, …,xa2,每个结果发生的概率记为p=p-a1,p-a1+1, …,pa2.累积前景价值为
(3)
式中:πh为累积权重函数,用来衡量风险对决策者的影响;v′(xh)为价值函数,用来衡量决策者的主观感受,其表达式为
(4)

计算累积权重函数时,首先计算单个概率权重函数.由于人们通常更倾向于去做小概率事件,所以概率权重函数为
(5)
(6)
式中:w+(ph)和w-(ph)分别为决策者面对收益和损失的概率权重函数;ph为xh的概率;φ和δ分别为风险收益态度系数和风险损失态度系数,经典取值为φ=0.61,δ=0.69.
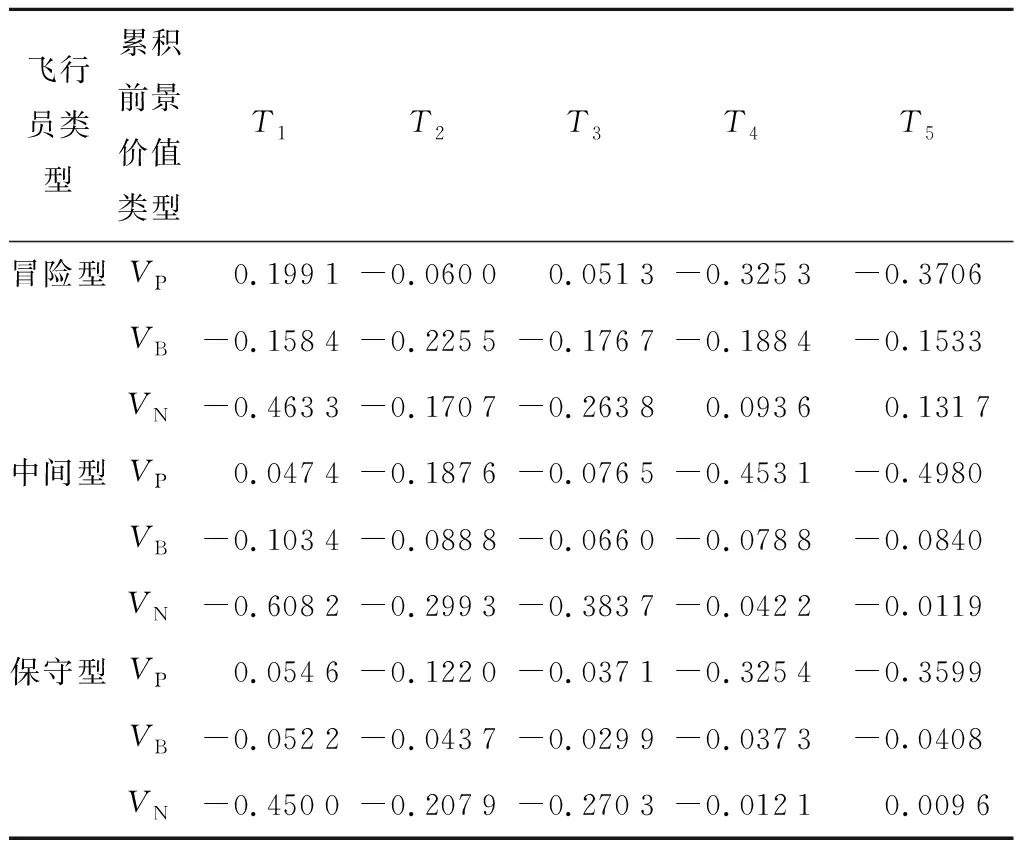
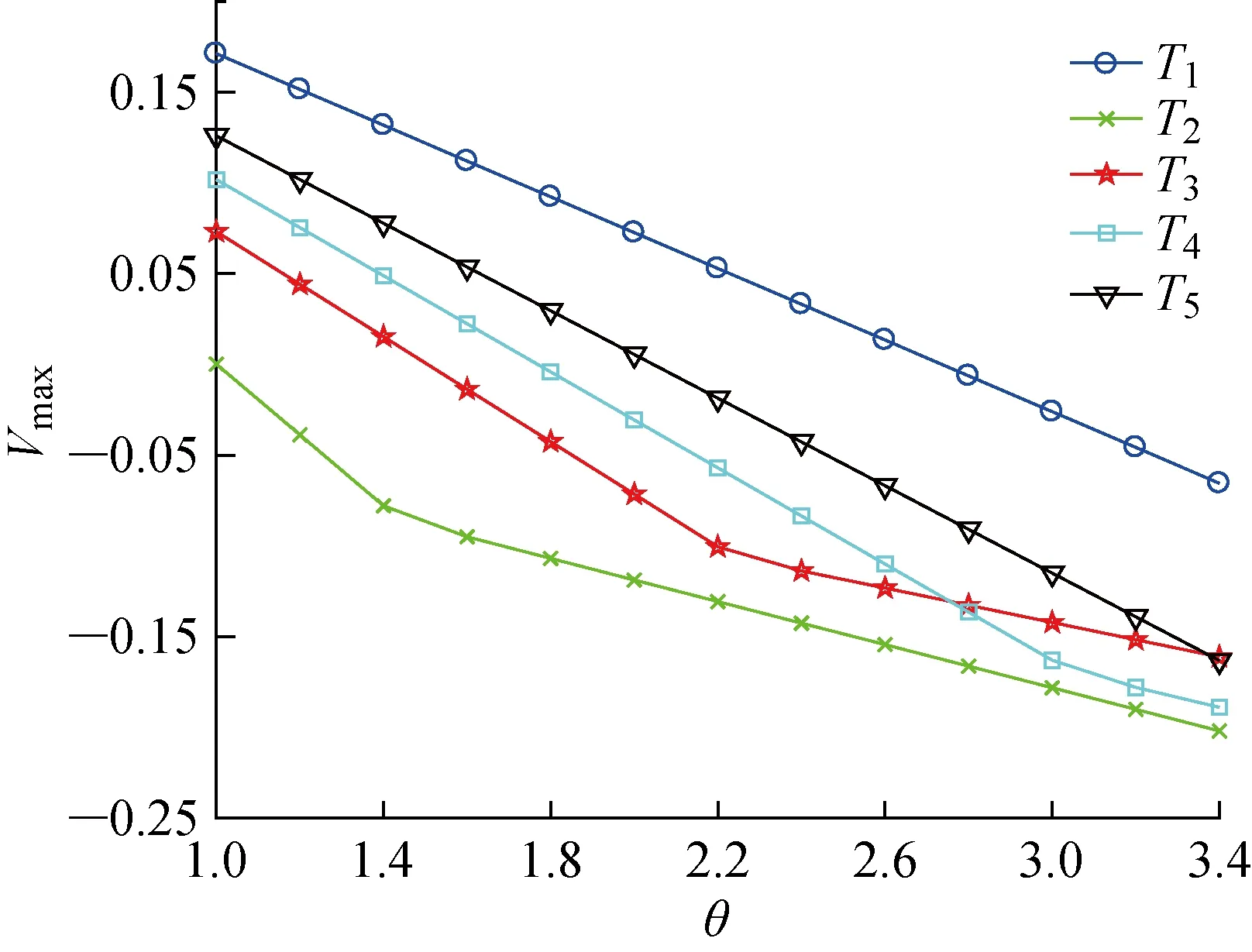
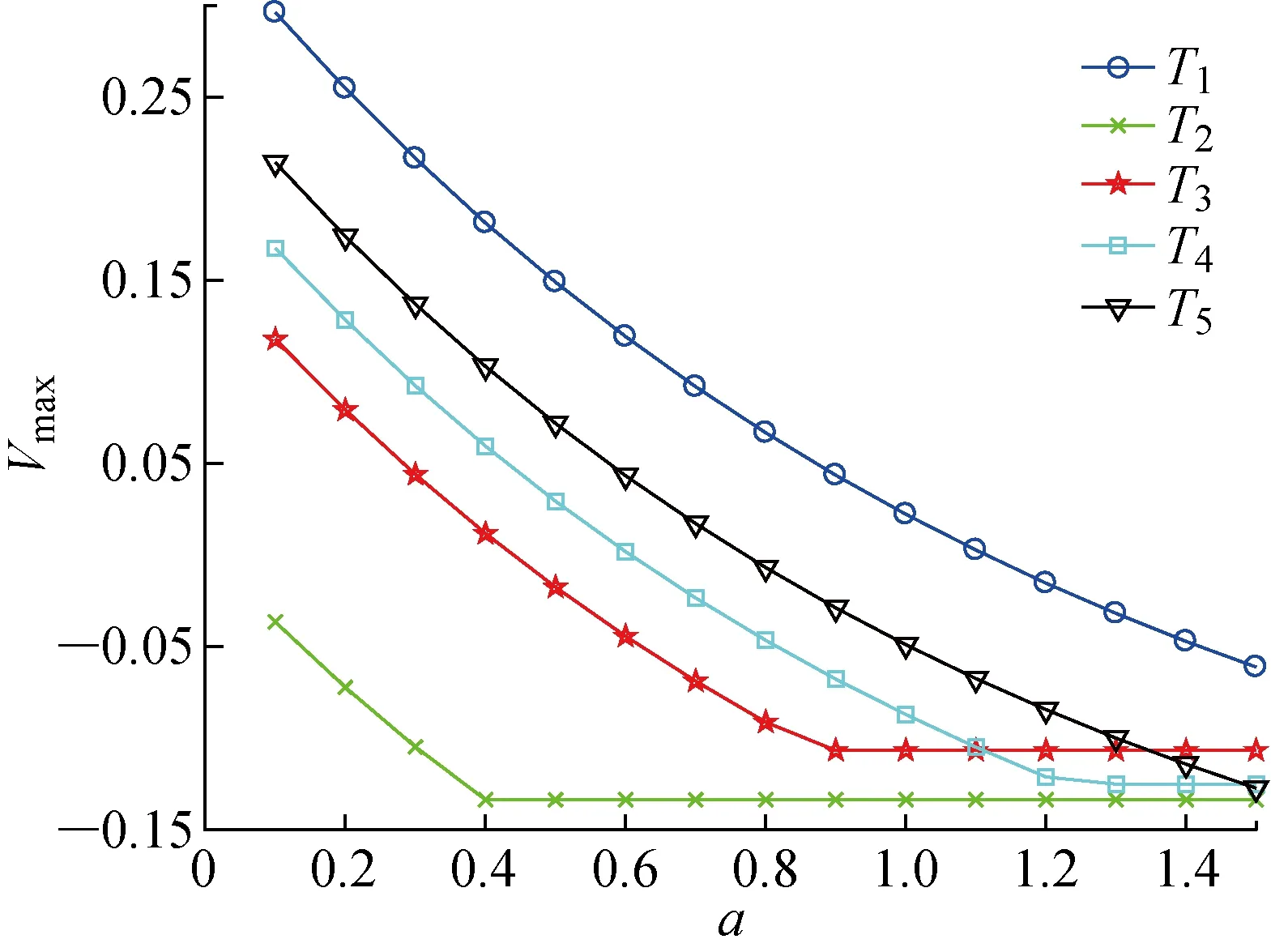
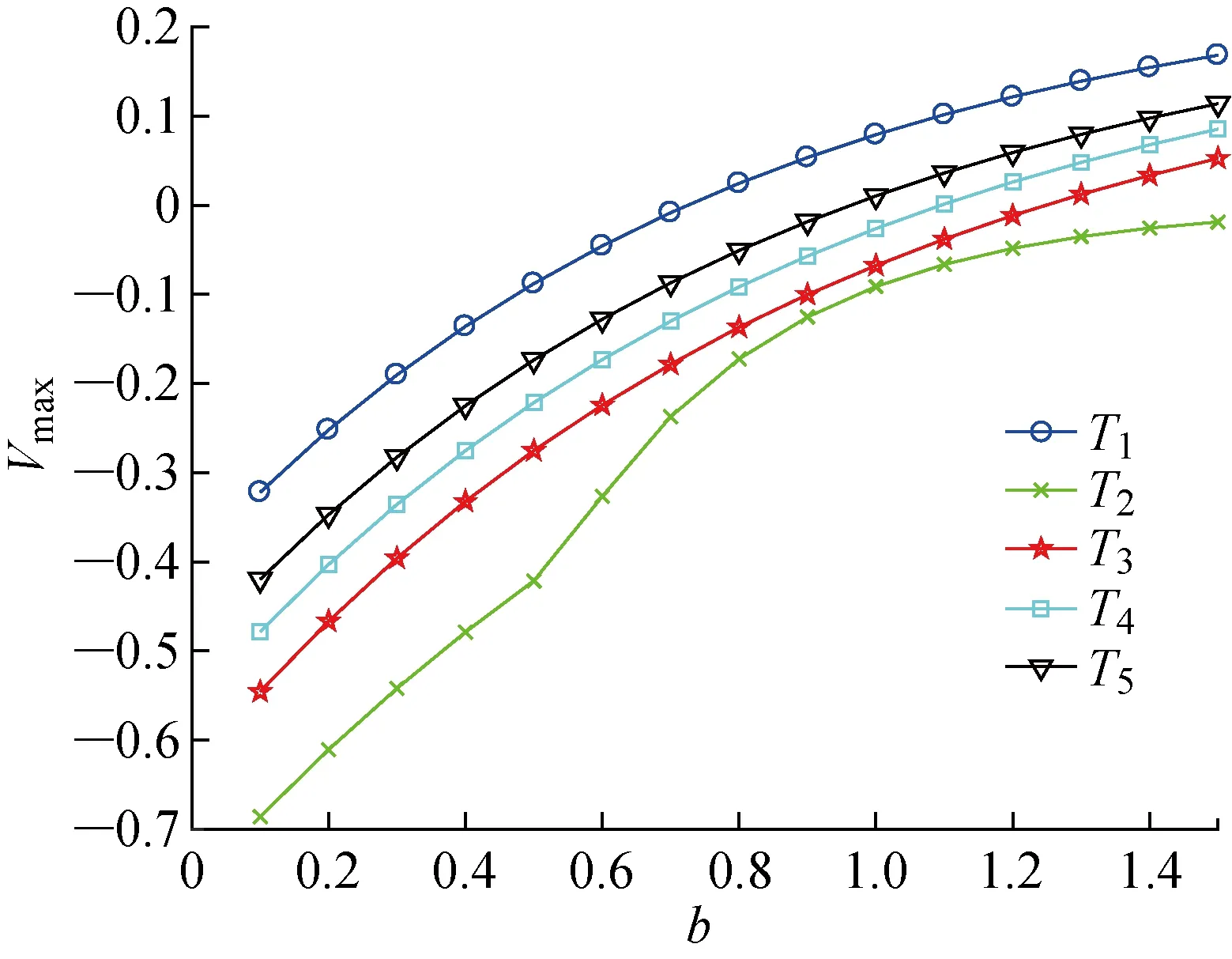
为了对权重进行累加,将a1+a2+1个结果按升序排序为x-a1< … πh= (7) 1.3.2改进累积前景理论 对于式(4),一般情况下决策者对损失更加敏感,但在现实生活中,也存在决策者对收益更加敏感的场景,因此引入收益敏感系数ζ,表达决策者对收益的敏感度.同时扩大a和b的取值范围,将其由前景理论认定的 0 (8) 式中:当θ=1,ζ>1时表示相对于损失,决策者对收益更加敏感;当θ>1,ζ=1时表示相对于收益,决策者对损失更加敏感. 针对以往的决策方法认为决策者处于完全理性的状态并且只能得到威胁排序结果的问题,提出一种基于累积前景理论和三支决策的无人机态势威胁评估方法. 该方法的数学描述和实现过程如下:假设敌机目标集合为T={T1,T2, …,Tm},每架敌机有n个指标:A={A1,A2, …,An}.评估矩阵为Z=(zij)m×n,目标为i∈{1, 2, …,m},指标为j∈{1, 2, …,n},zij为第i个目标在第j个指标上的值.Z为一个直觉模糊矩阵,每个数值都是直觉模糊数,zij=〈μij,vij〉.其中,uij和vij分别为直觉模糊数zij的隶属度和非隶属度.该方法首先利用直觉模糊逼近于理想值的排序(TOPSIS)方法计算每个目标的条件概率,从而得到威胁排序结果;之后利用结果矩阵和损失矩阵之间的关系计算每个目标的结果矩阵;最后根据相关公式计算每个目标执行不同动作时的累积前景价值,构建新的三支决策规则进行比较,得到威胁分类结果. 步骤一确定目标的正负理想解. 正负理想解分别为 2.2.3 营养支持 结核病为全身慢性消耗性疾病。病程长,临床症状重,术前营养状况差,加之手术创伤、修复需要,术后加强营养治疗对患者康复起着至关重要的作用。在静脉输入适量悬浮红细胞、新鲜冰冻血浆、白蛋白、脂肪乳、复方氨基酸、葡萄糖、维生素和微量元素的同时,还留置鼻胃管,予整蛋白型肠内营养剂、米汤、果汁等胃肠营养。每次鼻饲前先确认鼻胃管的深度,回抽胃液无明显胃储留再行鼻饲,鼻饲时尽量保持半卧位,避免因体位原因导致胃内容物反流而引起误吸,从而导致肺感染。拔除鼻胃管后鼓励并指导患者进食高热量、高蛋白、丰富维生素及矿物质饮食,促进机体康复。 不同类型的指标有不同的取值,效益型指标是指其值越大结果越好的指标,成本型指标是指其值越小结果越好的指标. 对于效益型指标,其正负理想解分别为 对于成本型指标,其正负理想解分别为 步骤二计算每个目标的相对贴近度. 首先,计算第i个目标到正负理想点的距离,计算公式为 (9) (10) 式中:D(Ti,Z+)和D(Ti,Z-)分别为目标Ti到正理想解和负理想解的距离;wj为第j个指标的权重. 之后,计算第i个目标的相对贴近度为 (11) 式中:Pr(C|Ti)为第i个目标在状态C中的条件概率;RC(Ti)为第i个目标的相对贴近度. 结果矩阵的构造方法与三支决策中的损失函数矩阵类似,矩阵中各元素分别表示在不同状态下执行3种操作的结果,矩阵中各元素可以表示为X=[xPPxPNxBPxBNxNPxNN].与损失函数不同的是,结果矩阵的值既可以为正也可以为负. 步骤一计算目标在每个指标下的损失函数矩阵. 指标的最大值和最小值分别用zmax和zmin表示.对于直觉模糊数表示的指标值,效益型指标的最大值和最小值分别为zmax=(1, 0),zmin=(0, 1),成本型指标的最大值和最小值分别为zmax=(0, 1),zmin=(1, 0). (12) 步骤二计算目标在每个指标下的结果矩阵. (13) 步骤三计算目标在多个指标下的综合结果矩阵. (14) 步骤一计算参考点. 首先使用记分函数将模糊矩阵转换为一般矩阵.本文采用经典的记分函数,表示为 Sij=μij-vij (15) 式中:Sij为直觉模糊数zij的记分函数值. 之后,求一般矩阵的指标平均值: (16) 为避免信息丢失,引入正负理想点作为另外两个参考点.同时,在实际空战过程中飞行员的偏好在很大程度上是模糊的,因此本文采用模糊分析法[15]来确定偏好权重. 首先根据决策者对不同参考点的偏好程度建立模糊矩阵P=[prw]u×u,u为参考点的个数,具体可表示为 (17) 之后对P进行一致化处理,先按行求和得到qr,再进行计算得到模糊一致矩阵Q=[qrw]u×u,表达式为 (18) (19) (20) (21) 式中:kr为第r个参考点的初始偏好权重;lr为第r个参考点的偏好权重. 步骤二计算每个目标的价值函数. 以矩阵的形式表示结果,矩阵内每个结果对应的价值函数为 (22) 步骤三计算每个目标的累积权重函数. 首先计算权重函数,表达式为 (23) (24) 式中:w+(pi)和w-(pi)分别为决策者面对收益和损失的概率权重函数;pi为第i个目标的概率. 之后,计算累积权重函数.价值函数单调递增,因此对价值函数进行排序,获得每个动作相关联的累积权重函数为 (25) (26) 式中:Pr(C|Ti) 为第i个目标Ti属于状态C的概率;Pr(C|Ti)为目标Ti不属于状态C的概率;为第i个目标属于状态C时采取动作k的价值函数;为第i个目标不属于状态C时采取动作k的价值函数;为Pr(C|Ti)时第i个目标采取动作k的累积权重函数;为Pr(C|Ti)时第i个目标采取动作k的累积权重函数;k=P,B,N. 步骤四计算每个目标在不同操作下的累积前景价值. 由价值函数和累积权重函数可以计算3种不同操作下的累积前景价值.当价值函数不同时,累积权重函数不同,对应的计算方法也不同,具体公式为 (27) (28) (29) 式中:Vi(aP|Ti)、Vi(aB|Ti)和Vi(aN|Ti)分别为对目标Ti采取接受、进一步研究和拒绝动作得到的累积前景价值. 最后,根据累积前景价值最大的原则,每个目标的三支决策规则为 (P)如果满足Vi(aP|Ti)≥Vi(aB|Ti)和Vi(aP|Ti)≥Vi(aN|Ti), 则Ti∈POS(C). (B)如果满足Vi(aB|Ti)≥Vi(aP|Ti)和Vi(aB|Ti)≥Vi(aN|Ti), 则Ti∈BND(C). (N)如果满足Vi(aN|Ti)≥Vi(aP|Ti)和Vi(aN|Ti)≥Vi(aB|Ti), 则Ti∈NEG(C). 采用文献[16]中的无人机数据进行实验分析,具体数据如下:假设我机在空战中遭遇5架敌机,敌机目标集合表示为T={T1,T2, …,T5} ;每架敌机选取8个评估指标,即类型、距离、角度、速度、高度、干扰能力、穿透能力和防护等级,评估指标集合表示为A={A1,A2, …,A8},其中,距离、角度和高度为成本型指标,其余为效益型指标.归一化多属性直觉模糊信息矩阵Z如表2所示. 表2 归一化多属性直觉模糊信息矩阵Tab.2 Normalized multi-attribute intuitionistic fuzzy evaluation information matrix 通过公式计算得到每个目标的条件概率、不同状态下的权重函数及结果矩阵,如表3~5所示. 使用记分函数将直觉模糊信息矩阵转换为一般矩阵,利用公式计算得到η=(0.365,0.135, 0.5), 表3 每个目标的条件概率Tab.3 Conditional probability of each target 表4 每个目标的权重函数Tab.4 Weight function of each target 表5 每个目标的结果矩阵Tab.5 Outcome matrix of each target 通过计算得到指标平均值、正理想点和负理想点,再乘以对应的偏好权重,即可得到本文需要的参考点,具体算式为 0.518 8×0.5=-0.172 6 利用参考点、结果矩阵计算得到相应的价值函数,并由价值函数和权重函数计算得到相应的累积前景价值,如表6所示.其中,VP、VB和VN分别为目标采取接受、进一步研究和拒绝动作时的累积前景价值. 表6 每个目标的累积前景价值Tab.6 Cumulative prospect value of each target 由表3可知,基于综合直觉模糊信息矩阵的态势评估的排序结果是T1>T3>T2>T4>T5.由表6可知,基于决策规则的直觉模糊信息矩阵的客观分类结果是POS(C)={T1},BND(C)={T2,T3},NEG(C)={T4,T5}.这意味着首先应该攻击和干扰T1,不攻击和干扰T4和T5,需要更多的信息判断是否要攻击T2和T3. 3.2.1评估结果对比与分析 为了进一步说明本方法的有效性和优越性,本文与文献[7-8,16]的决策方法进行对比,简要对4个方案的评估结果进行分析.其中,文献[7]采用直觉模糊VIKOR方法,文献[8]采用三支决策的方法,文献[16]采用直觉模糊相似度量推理模型(IFSMRM)方法.4种决策方法仿真分析时使用同一组数据,决策结果对比如表7所示. 表7 实验结果对比Tab.7 Comparison of experimental results 在4种方法的评估结果中,本文方法与三支决策方法得到的排序结果一致,分类结果有所不同,说明决策者的心理态度会影响威胁评估结果.在战场中考虑决策者心理具有研究价值,验证了本文方法的正确性.本文方法与IFSMRM方法所得结果在目标T1和T3上不一致,与T3相比,T1的速度更快,类型指标的值更大,表示作战能力更强,更容易发起攻击,因此T1的威胁等级更高;IFSMRM方法预先设定了7个威胁等级,目标T1和T3在相同的威胁等级中,T2被划分到下一个威胁等级中;T3与T2相比,距离、角度和高度等略小,但T3的类型也略小,表示其作战能力稍差,因此二者的威胁程度相差不大,本文方法将T2与T3划分到同一个区间是合理的,并且将目标划分到3个区间符合人类心理认知,验证了本方法的合理性.本文方法与VIKOR方法得到的排序结果不一致,与T3相比,T1的速度更快,类型指标值更大,表示作战能力更强,更容易发起攻击,因此T1的威胁等级更高;与T4相比,T2的速度较小,距离较远,但其类型指标值远大于T4,表示其作战能力远强于T4,有能力发动突然袭击,因此T2的威胁等级更高,显然本文方法更符合客观分析. 与文献[7]使用的VIKOR方法相比,本文方法得到的威胁评估结果更符合实际认知,且能提供客观分类结果,更好地为决策者提供决策支持.与文献[8]仅使用三支决策对比,两者使用同样的方法计算三支决策的条件概率,三支决策中威胁排序结果与概率大小保持一致,因此两种方法得到的排序结果相同;同时本文方法将累积前景理论和三支决策相结合,将决策者的心理考虑到评估结果中,不同决策者可以根据自己的风险偏好选择偏好权重,得到不同的参考点;同一决策者面对不同的战场态势,得到不同的参考点;由不同的参考点得到不同的分类结果,符合真实战场环境,解决了以往态势评估未考虑决策者心理的问题.与文献[16]使用的IFSMRM方法对比,本文采用三支决策的方法,不仅得到了威胁排序结果,而且得到了对目标的具体操作,不同域的目标有不同的操作,有利于飞行员进行快速决策,解决了当前决策困难、易产生误判的问题.并且无需事先设定威胁等级,可根据新的三支决策规则实时地做出威胁分类,选择优先作战目标. 4种方法的目标威胁评估值如图1所示.4种方法均通过比较目标威胁值得到威胁排序结果,即表7中的排序结果. 图1 4种方法的目标威胁评估值Fig.1 Threat assessment results of 4 methods 3.2.2复杂度对比与分析 根据4种方法的具体流程,可得其时间复杂度均为O(mn).随机进行10次实验,方法耗时结果如图2所示.在4种方法对比中,虽然本文方法耗时较高,但本文方法和其他方法具有相同且较低的时间复杂度,耗时仍然能够满足战场实时性要求. 图2 4种方法的耗时Fig.2 Time of 4 methods 为了验证不同类型的飞行员在面对相同的战场环境时会有不同的态势评估结果,采用了3种典型的参数组合,如表8所示.表8中参数a=0.37,b=0.59,ζ=1,θ=1.51来源于文献[17]中的实验值;参数a=1,b=1,ζ=1,θ=2.25以及参数a=1.21,b=1.21,ζ=1,θ=2.25来源于文献[14]中的实验值;权重函数参数均来源于文献[14]中的实验值. 表8 3种典型的参数组合Tab.8 3 typical parameter combinations 为了清楚说明决策参数对目标态势评估的影响,通过数值仿真得到了3种类型下的目标态势评估关系.由表9和表10可知,在3种典型参数组合情况下,威胁评估结果总体比较稳定,但是目标分类结果不同.因为威胁评估排序结果与条件概率的排序保持一致,所以不同类型的飞行员只影响分类结果.首先,冒险型决策者认为目标T2和T3都应该攻击;中间型和保守型认为目标T2和T3需要更多的信息来判断是否需要攻击,说明不同类型的飞行员决策结果不同,受到了飞行员主观心理因素的影响.其次,中间型和保守型的分类结果相同,但累积前景价值不同,保守型的目标T4和T5的累积前景价值更小,说明其不想攻击的意愿更强烈,该决策结果符合人类认知.总体结果表明,在实际空战中要充分考虑飞行员的心理,对飞行员类型进行判断,从而使态势评估结果更符合实际作战情况. 表9 3种类型决策者的累积前景价值 表10 3种类型决策者的结果Tab.10 Results of 3 types of decision makers 为研究不同参数取值对态势评估结果的影响情况,分析不同参数的灵敏度,如损失规避系数θ、风险态度系数a和b,使用最大累积前景价值Vmax=max{VP,VB,VN}比较态势评估结果.损失规避系数θ对不同目标的最大累积前景价值Vmax的影响如图3所示. 由图3可知,随着损失规避系数θ的不断增加,目标T1、T2、T3、T4和T5的最大累积前景价值均处于下降趋势,但目标所在的域不同,代表其威胁程度也不同.具体而言,随着θ的增大,目标T1仍处于正域,采取攻击操作的累积前景价值不断减小,说明目标T1的威胁评估结果随θ的增大而减小.随着θ的增大,目标T2和T3从正域过渡到边界域,采取不攻击操作的累积前景价值不断减小,说明目标T2和T3的威胁评估结果随θ的增大而减小.随着θ的增大,目标T4和T5仍处于负域,采取不攻击操作的累积前景价值不断减小,说明目标T4和T5的威胁评估结果随θ的增大而增大.综上说明,随着损失规避系数θ的不断增大,目标的威胁评估结果也呈现出不同的变化趋势. 图3 损失规避系数θ扰动Fig.3 Perturbation of loss avoidance coefficient θ 图4为风险态度系数a对不同目标的最大累积前景价值Vmax的影响.由图4可知,随着a不断增加,目标T2和T3的累积前景价值较大值均呈现出先下降后缓慢上升的趋势;目标T1、T4和T5的累积前景价值较大值均呈现出下降趋势.随着a不断增大,决策者类型从冒险型不断向保守型过渡.在这个过程中,目标T2和T3从正域过渡到边界域,目标T4从负域过渡到边界域;目标T3、T4和T5的排序发生微小变化,说明不同类型的决策者会影响排序和分类结果. 图4 风险态度系数a扰动Fig.4 Perturbation of risk-return attitude coefficient a 图5为风险态度系数b对不同目标的最大累积前景价值Vmax的影响.由图5可知,随着b不断增大,目标的累积前景价值最大值均呈现出上升的趋势.但目标所在的域不同,代表其威胁程度也不同.具体而言,随着b的增大,决策者类型从冒险型向保守型不断过渡,在这个过程中,目标T1、T2和T3仍处于正域或边界域,采取攻击操作的累积前景价值不断增大,说明目标的威胁评估结果随b的增大而增大;目标T4和T5处于负域,采取不攻击操作的累积前景价值不断增大,说明目标T4和T5的威胁评估结果随b的增大而减小.综上说明,随着风险态度系数b的不断增大,目标的威胁评估结果也呈现出不同的变化趋势. 图5 风险态度系数b扰动Fig.5 Perturbation of risk-return attitude coefficient b 针对无人机态势评估决策困难及未考虑复杂外界环境对决策者的影响问题,提出一种基于累积前景理论的三支决策模型,并据此进行了仿真实验,主要结论如下: (1) 与传统的态势评估方法相比,基于累积前景与三支决策的态势评估方法在对目标进行决策时,能够使得分类结果更加合理,有利于飞行员做出快速决策,解决了决策困难的问题,更好地满足战场快速打击的需求. (2) 与传统的三支决策方法相比,本方法在决策过程中引入了累积前景价值,不同的决策者有不同的风险偏好,同一决策者在面对不同战场态势时心理也会发生变化,从而得到不同的参考点,可以反映出决策者的决策偏好和风险态度,使决策结果更符合现实场景. (3) 不同类型的飞行员在面对相同目标时会得到不同的态势评估结果,表明在实际空战中要充分考虑飞行员的心理,对飞行员类型进行判断,从而使态势评估结果更符合实际作战情况.2 基于累积前景理论和三支决策的态势评估方法
2.1 计算三支决策的条件概率



2.2 计算结果矩阵




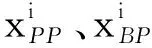
2.3 计算每个目标的累积前景价值

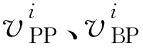
3 仿真及实验分析
3.1 仿真分析
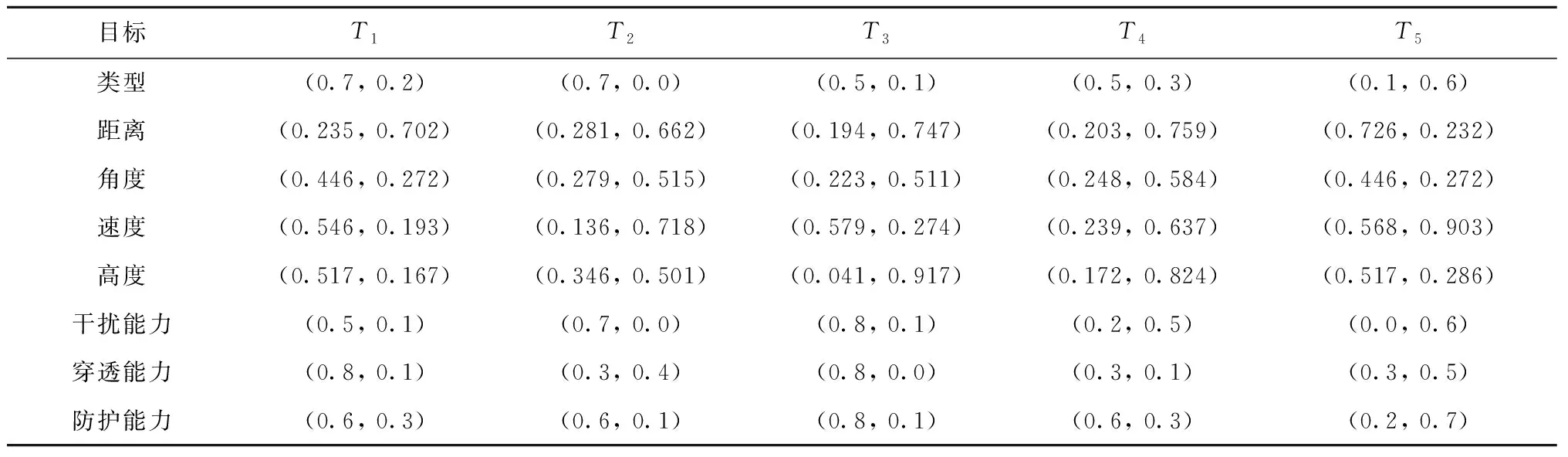

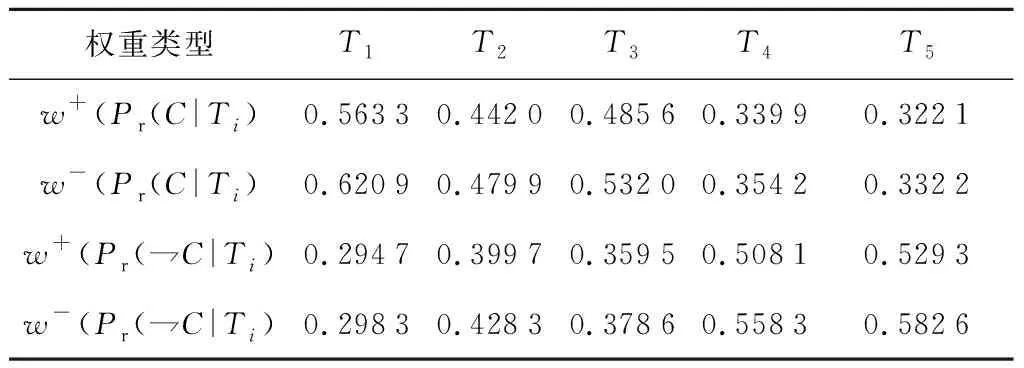



3.2 实验对比与分析



3.3 决策参数分析


3.4 参数敏感性分析
4 结论

