前瞻性研究非独立性二分类结局的Poisson回归方法

王俊苹 沈灵智 卢肇骏 寇 硕 郑卫军

1 浙江中医药大学公共卫生学院，310000 浙江 杭州；2 浙江省疾病预防控制中心，310000 浙江 杭州

前瞻性研究以二分类变量作为研究结局是常见的现象，研究者习惯采用logistic回归获得的优势比(odds ratio，OR)反映暴露对结果的关联性；但是在队列研究中更推荐直接计算相对危险度(relative risk，RR)，采用logistic回归计算的OR值往往会高估效应，尤其在结局事件比较常见时[1-3]。2004年Zou[4]提出利用修正Poisson回归法计算RR值，该法采用“三明治法”(sandwich variance estimator)矫正标准误差，从而获得了比较稳健的误差估计值，目前这种方法在诸多队列研究案例中得到广泛应用[5]。运用修正Poisson回归模型对服从二项分布的资料进行分析能给实际研究带来很多便利，这主要包括：通过一种稳健的误差方差估计法(sandwich variance estimator)校正RR值以解决普通Poisson回归对RR的估计误差较大的问题，有实用的标准软件(如SAS的GENMOD过程)等。与标准logistic回归模型相似，修正Poisson回归要求观测值之间必须是相互独立的，否则会导致统计推断的系统性偏差。但在实际研究中，样本之间许多都是具有相互关系的观测值，即观测数据并非来自完全独立的随机样本。传统的修正Poisson方法无法应对非独立性结局事件的回归建模，比如多中心队列研究(此类结局事件通常存在聚集性)。因此，本研究基于国内外研究进展，并结合SAS软件，探讨如何运用SAS软件结合修正Poisson回归分析非独立性数据。

1 方法介绍

1.1 普通Poisson回归

Poisson分布指的是在一个极大人群、空间和时间范围内，观察对象某种现象发生数的分布。常用于稀有事件的发生次数的概率分析，以发生数作为因变量，构建回归模型，来探讨影响事件发生的因素。

Poisson回归是一种将对数和二项分布连接起来的广义线性模型。该模型可以被写成：

log[λ(Xi)]=β0+β1X1i+β2X2i+...+βKXKi

(1)

在这种情况下，若要计算变量和因变量的数量依存关系，可以基于公式(1)计算得到

因此，Poisson回归可以计算RR值来反映暴露因素对结局事件发生的影响。

1.1.1 案例1

对45 例来自3个社区(community)的非器质性心脏病且仅有胸闷症状就诊者进行分析研究，以探讨吸烟与24 h早搏次数的关系。影响因素是X1，是否吸烟(1=吸烟，0=不吸烟)；结局变量是Y1，24 h早搏次数(离散型定量数据，呈Poisson分布)。其数据库结构见表1。

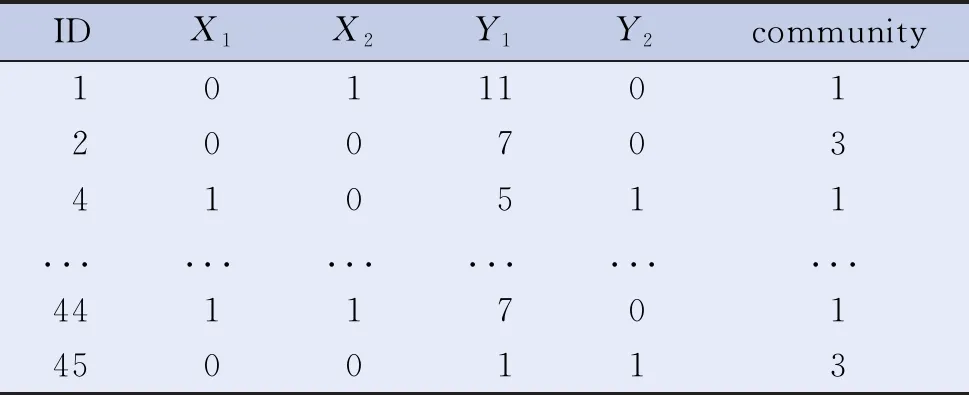
表1 案例1、案例2、案例3的数据库结构

1.1.2 24 h早搏数的Poisson回归SAS程序

首先，以24 h早搏数作为因变量构建Poisson回归模型，自变量包括X1，利用SAS“PROC GENMOD”进行模型的构建，SAS程序如下：

PROC GENMOD DATA =A;

MODEL Y1 =X1/LINK = log dist = Poisson;

ESTIMATE ′adjusted RR for X1′ X1 1/EXP;

RUN;

1.1.3 结果分析和解读

通过SAS程序，计算得到X1的RR=1.31，RR的95%CI为(1.04，1.64)，又因为X1代表“是否吸烟(1=吸烟，0 =不吸烟)”，说明吸烟者出现早搏的风险是不吸烟者的1.31倍。

传统的Poisson回归可以广泛用于呈Poisson分布离散型结局事件，特别是在偏态分布的情况下，可以代替线性回归进行数据分析。

1.2 修正Poisson回归

Poisson回归通常适用于处理罕见结局事件的前瞻性研究资料，即服从Poisson分布的资料。当将其应用于服从二项分布的资料时，对RR的估计误差便会增大，但是这个问题可以通过一种稳健的误差估计法即“三明治法”(sandwich variance estimator)得到校正，被称为修正Poisson回归，这种方法由Zou[4]在2004年提出。

1.2.1 案例2

同样基于3个社区的非器质性心脏病且仅有胸闷症状就诊者，调查的暴露因素是X1，是否吸烟(1=吸烟，0=不吸烟)；协变量是X2，是否喝咖啡(1=喝、0=不喝)；结局变量是Y2，冠心病是否复发(1=复发，0=未复发)。

1.2.2 修正Poisson回归的SAS程序

修正Poisson回归法基于广义估计方程原理， 利用SAS的GENMOD过程中 REPEATED 语句估计得到更为稳健的误差方差，解决了普通Poisson回归估计参数区间过于保守的问题。SAS程序如下：

PROC GENMOD DATA =A;

CLASS ID;

MODEL Y2 =X1 X2/DIST = Poisson LINK =log;

REPEATED SUBJECT =ID;

ESTIMATE ′adjusted RR for X1′ X1 1/EXP;

RUN;

1.2.3 结果分析和解读

GENMOD过程分析结果中，X1的RRa=3.06，RRa的95%CI为(1.11，8.49)，又因为X1代表“是否吸烟(1=吸烟，0 =不吸烟)”，说明调整混杂因素后吸烟者冠心病复发的概率是不吸烟者的3.06倍，见表2。可以看出在与普通Poisson回归相同的情况下，得到了更为精确的参数区间估计范围。

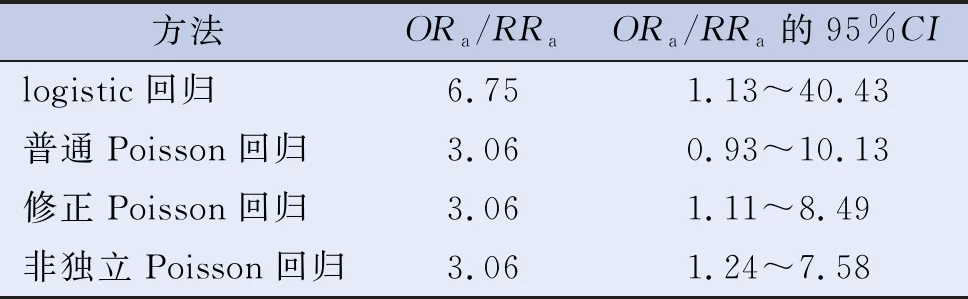
表2 3个社区冠心病患者复发与吸烟的关系研究

1.3 针对非独立性数据Poisson回归

在医学研究中，很多事件的发生是非独立性的。例如疾病的聚集性或家族性，或传染性疾病。修正Poisson回归是在独立数据的背景下提出的，并通过分析和模拟证明在这种情况下是可以使用的[6-8]。广义估计方程作为一种证据性较强的方差估计方法并考虑了数据聚集性，因此可以通过使用广义估计方程来校正标准误差，而不是采用通常应用于独立数据的方差估计方法。

1.3.1 案例3

同样基于3个社区的非器质性心脏病且仅有胸闷症状就诊者，调查的暴露因素X1，是否吸烟(1=吸烟，0=不吸烟)；协变量X2，是否喝咖啡(1=喝、0 =不喝)；聚集性变量社区，community(1、2、3)；结局变量Y2，冠心病是否复发(1=复发，0=未复发)。

1.3.2 非独立Poisson回归的SAS程序

非独立Poisson回归将稳健误差方差估计法扩展应用到非独立性二分类数据中，使用稳健误差方差估计法解释聚类效应及Poisson模型作为二分类数据的工作模型。使用Zou[4]描述修正Poisson的SAS代码来完成计算，其中将SAS PROC GENMOD的重复语句中单个体标识符更改为聚集性标识符[9]。SAS程序如下：

PROC GENMOD DATA =A;

CLASS city;

MODEL Y2 =X1 X2/DIST = Poisson LINK =log;

REPEATED SUBJECT =community;

ESTIMATE ′adjusted RR for X1′ X1 1/EXP

RUN;

1.3.3 结果分析和解读

在本案例中，X1的RRa=3.06，RRa的95%CI为(1.24，7.58)，又因为X1代表“是否吸烟(1=吸烟，0 =不吸烟)”，说明吸烟者冠心病复发的概率是不吸烟者的3.06倍，见表2。可以看出在相同的情况下与修正Poisson回归相比，得到了更为精确的参数区间估计范围。将聚集性变量“社区”纳入回归模型后，不仅可以改善原本回归分析中面临的残差不独立性的问题，而且可以进一步通过聚集性变量(社区)减少残差，提高分析效率。

2 实例分析

本研究基于中国健康与养老调查2011—2018(CHARLS 2011—2018)的数据，对13 283名45～100岁的中老年人进行分析研究，以探讨我国中老年人腹型肥胖与死亡的关系。该研究是多中心的前瞻性队列研究，影响因素包括：X1，是否腹型肥胖(1=腹型肥胖，0=非腹型肥胖)；X2，性别(1=男，0=女)；X3，年龄(1=60岁以上，0=45～60岁)；X4，户籍(1=非农业，0=农业)；X5，婚姻(1=未婚，2=结婚)。聚集性变量为城市(1=东部城市，2=中部城市，3=西部城市)。

研究分别采用logistic回归、普通的Poisson回归、修正Poisson回归、非独立Poisson回归进行分析，调整混杂因素和中心效应后，腹型肥胖死亡的概率是非腹型肥胖者的0.89倍。见表3。

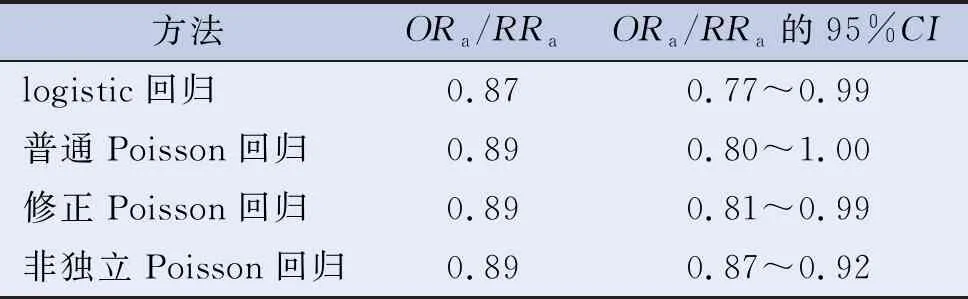
表3 不同的分析方法中老年人腹型肥胖(X1)与死亡的关系

3 讨论

本研究使用具有可交换相关结构的广义估计方程来解释聚集性，通过模拟及实证非独立的前瞻性数据，研究非独立Poisson回归方法估计相对风险的性能，结果显示该方法在少量或大量的集群条件下均表现较好。

与logistic回归法比较，普通Poisson回归法适用的资料类型范围更广，除二分类结局外还可应用于处理结局为离散型定量数据。当结局事件的发生率较为常见(>10%)时，OR值往往会明显高估或低估真实的RR值，进而对临床和公共卫生的正确决策产生影响[10-11]，这时直接计算RR值较为恰当。与普通Poisson回归法比较， 修正Poisson回归法在参数点估计值相同的情况下，得到了更为精确的参数区间估计范围，从而解决了普通Poisson回归法对参数区间估计过于保守的问题。与修正Poisson回归法比较，非独立Poisson回归法在参数点估计值相同的情况下，得到了更为精确的参数区间估计范围，从而解决了非独立性数据间具有相关性的问题。Yelland等[12]通过 SAS 软件模拟数据研究也证实了这一点。

本研究结果表明，在非独立Poisson回归方法中将广义估计方程应用于处理非独立的前瞻性数据是合适的。修正Poisson回归法作为负二项回归的替代方法被提出，用以估计独立数据背景下的相对风险，其中将其原理应用在聚类数据背景下的性能目前才被研究，并通常使用广义估计方程解释聚集性[13-14]。除了使用广义估计方程来解释数据聚集性外，另一种替代方法是拟合具有随机聚类效应的混合模型。区别于广义估计方程，第二种方法必须假设随机效应的分布比较难以验证，并且对其错误的解释可能对结果产生重大影响。

因此，对于常见结局事件的非独立前瞻性研究，使用非独立Poisson回归法来计算暴露因素的RR值是一种较为简单准确的分析方法，并可利用SAS软件包中的PROC GENMOD程序来实现。