追本溯源巧串链 转识成智现光华*——以简谐运动大单元教学为例

陈斌 张林海|江苏省靖江高级中学

古希腊哲学家赫拉克利特早就说过“博学不能使人智慧”，哈佛大学一位教授研究了很多诺贝尔自然科学奖的获奖者，也得出一个结论：创新与知识的多少没有正相关的关系。因此，教育的关键不是灌输知识内容，而是点燃智慧火焰，即要努力将知识转化为智慧。要实现转识成智，就需要活化知识。活化知识至少包含三层递进的意蕴：一是知识的运用，即能够在真实情境中运用知识，并能体验到发现的快乐；二是知识的贯通，即要消除知识碎片化的割裂状态，让学生既见树木又见森林；三是知识的创新，这既是人追求美好生活的需要，也是人的创造本性使然[1]。转识成智教育的魅力在于：它根据学生的认知规律，立足鲜活的生活、生产实践，用大单元思维统整知识结构，构建“问题·体悟·想象”三维立体路径，引领学生以快乐为舟、问题作帆来激活好奇心，以实践引路、体悟架桥来提升探究性，以自由当风、想象为翼来腾飞创造力[2]，进而在追本溯源的知识探索中孕育和生长智慧。

下面，笔者以人教版普通高中教科书《物理》选择性必修第一册第二章《机械振动》第1～5节作为一个单元，开展指向学科核心素养的大观念、大任务与大问题的统筹规划和科学设计[3]。笔者努力提升站位、改变格局，依据课程标准、依托教材资源、依靠学情分析，聚焦简谐运动的两个理想化模型——弹簧振子和单摆，将简谐运动的知识条件化、结构化、情境化，并将简谐运动与其他机械运动进行比较，帮助学生实现有意义的建构。可以这么说，简谐运动的运动学特征、动力学特征、能量关系、周期公式就像一颗颗璀璨夺目的珍珠，将简谐运动的和谐美装扮得分外亮眼，而运用“运动与相互作用”观、能量观这样的大观念串线，把简谐运动与已学过的匀变速直线运动、平抛运动、匀速圆周运动等典型的运动进行联系与甄别，整个动力学内容就串成了一条晶莹剔透的项链，顿时变得光彩照人。此情此景，定会让学生彻悟物理规律的真谛，实现转识成智教育的目标追求。

一、拾贝——描述运动图像

机械振动是物体或物体的一部分在某一位置附近的往复运动。如钟摆的来回摆动、琴弦的振动、树枝在风中摇曳、浮标在水中上下浮动等。

【体悟1】笔者打开电脑“录音机”，请一个学生对着电脑讲一段话或唱几句歌，然后笔者打开播放工具（课前将播放器设置为“单曲循环”，将可视化效果设置为“波形”，电脑与教室里的大屏幕连通），学生在听到声音时，就能看到播放器界面中出现幅度随声音强弱变化的图线。笔者让学生边看边听，体悟这个图线的意义。

【体悟2】笔者出示一段心电图图纸，让学生观察并体悟心电图的特征，然后经由合作探讨，分析心电图的横坐标和纵坐标的意义。

【归纳】播放器界面中呈现的是声音强弱随时间变化的x-t图像；心电图图纸中以时间为横坐标、心跳的幅度为纵坐标，它描绘的是心跳幅度随时间变化的x-t图像。生活、生产中，地震仪监测地震时用的也是这种方法，管弦乐器、琴键的吹拉弹奏中，用录音设备来记录声音的振动也用到类似的方法……可见，位移—时间（x-t）图像是我们描述机械振动最直观的方法。

【问题】简谐运动的运动特征是怎样的？它的x-t图像及振动方程又是怎样的？

简谐运动是最简单而又和谐的机械振动，它有两个理想化模型：弹簧振子和单摆。我们可以通过理想化模型来探究、体悟。

【探究1】水平弹簧振子振动的x-t图像。

笔者演示实验：如图1所示的水平弹簧振子装置中，振动小车左右两侧系有相同的弹簧，在近乎光滑的水平平台上做简谐运动。小车上装有位移传感器，数据采集器通过蓝牙将各时刻小车的位置信息发送给电脑，电脑对数据处理后，在屏幕上呈现出水平弹簧振子的x-t图像。笔者再将它投影到大屏幕上，让所有学生都能一目了然。

图1 水平弹簧振子实验装置

【探究2】单摆摆动的x-t图像。

学生分组实验：将一个盛沙的漏斗悬挂在固定支架上，在漏斗的下方水平放置一块中央画有直线的薄板，使漏斗在一个固定的竖直平面内做小角度的摆动，同时匀速拉动漏斗下方的水平薄板，观察从摆动的漏斗中流出的细沙在薄板上形成的曲线。

在学生分组实验中，笔者适时引导点拨。漏斗的摆动与薄板的匀速直线运动具有同时性，因此，细沙的轨迹图即为漏斗摆动的x-t图像。

【总结】简谐运动的运动学特征：物体的位移与时间的关系遵从正弦函数规律，即它的振动图像是一条正弦曲线。其振动方程为x=因此，我们常用振幅、周期、相位来描述简谐运动的运动特征。

相较而言，简谐运动比匀速直线运动、匀变速直线运动、平抛运动、匀速圆周运动这四种典型的机械运动都更为复杂，但其特殊性也不言而喻，仅从观察到的运动表象我们就能感受到一种和谐美。

二、采珠——探寻动力学规律

简谐运动是x-t图像为正弦函数的周期性振动，但它为什么会这样运动呢？这就要弄清振动质点的受力情况。因此，研究简谐运动的“运动与相互作用”的关系显得极为重要。

【体悟】水平弹簧振子振动时的受力情况。

水平弹簧振子振动过程中，振动小球一旦离开平衡位置（弹簧的自由伸长处），就会受到弹簧的弹力作用，弹力提供回复力。根据胡克定律F回=-kx，由牛顿第二定律可知，加速度，可见，水平弹簧振子的简谐运动是速度大小和方向、加速度大小和方向均在时刻变化的变加速运动。

学生提出疑问：这样的变加速运动与前面学过的各种运动相比，又有怎样的动力学和能量特征呢？笔者带领学生换一种方式加以探究。

【理论探究】基于匀速圆周运动在某个坐标轴上的投影的位移—时间图像为正弦曲线，我们可借用匀速圆周运动的投影情境来着手探究。

如图2所示，一质量为m的质点自x轴正方向上的M点，以角速度ω做半径为A的匀速圆周运动，观察其在y轴上的投影的运动情况，写出其位移、速度、加速度的表达式。

图2 用匀速圆周运动投影情境表征简谐运动

质点从M点做匀速圆周运动，经时间t到达图中P点，其对应的圆心角θ=ωt，此时

位移y=Asinθ=Asinωt

速度vy=vcosθ=ωAcosωt

加速度ay=ansinθ=-ω2Asinωt

探究发现：质点运动投影的y-t图像为正弦函数曲线，表明匀速圆周运动在坐标轴上的投影就是一个简谐运动。

从以上探究还可发现，除y-t图像为正弦函数曲线外，其v-t、a-t图像也为初相不同的正弦函数曲线。

这样，通过投影法，我们不必用微分方程，就可以清楚地认识到位移y、速度v、加速度a三者的关系，进而能从动力学角度更好地理解简谐运动。

因ay=-ω2Asinωt=-ω2y

故F回=may=-mω2y

现将y换成我们的习惯表述x

即有F回=-kx

这里，k为回复系数，k=mω2。对水平弹簧振子而言，k就是弹簧的劲度系数。

【总结】简谐运动的动力学特征：物体在运动方向上所受的力与它偏离平衡位置的位移大小成正比，并且总是指向平衡位置。

【问题1】简谐运动是周期性的往复运动，它的周期是怎样的呢？

由k=mω2可得

由公式可以看出，简谐运动的周期T与振幅A无关。

【体悟】单摆摆动中的回复力。

观察一摆长为l，摆球质量为m的单摆，它在竖直面内摆角θ＜5°。

师生共析：摆球在摆动中受到重力mg和摆线拉力FT的作用，其中，重力的切向分力提供回复力，摆线拉力与重力的法向分力的合力提供向心力。

【论证】单摆的摆动是简谐运动。

因为单摆的回复力F=mgsinθ

当摆角θ很小时，且F与x方向

相反

即有F=-kx（回复系数

所以，单摆的运动是简谐运动，运动的平衡位置在最低点。

【问题2】单摆的周期公式是怎样的？根据周期公式则

至此，可以安排学生进行“用单摆测量重力加速度”的实验。学生测出单摆的摆长l和周期T，可应用周期公式求出重力加速度，也可测多组数据用图像法借助斜率求出重力加速度。

【总结】单摆是以最低点为平衡位置，沿圆弧曲线的简谐运动，它也是一个变加速运动。

【探究】简谐运动中的能量关系。

（1）对水平弹簧振子：动能和弹性势能发生相互转化，机械能守恒。

（2）对单摆：动能和重力势能发生相互转化，机械能守恒。

弄清了简谐运动的运动学特征、动力学特征和能量关系后，学生将有能力论证某种运动是不是简谐运动，它的运动周期如何，以及能量如何转化。教师可以在此基础上提出竖直弹簧振子模型，引发学生思考，拓展其思维的深广度。

【问题3】竖直弹簧振子的振动是简谐运动吗？它在振动过程中，机械能守恒吗？

根据弹力与重力的合力提供回复力，即可论证竖直弹簧振子的振动是简谐运动，只是它的平衡位置从弹簧的自由伸长处下移了x0=它在振动过程中，只有系统内的重力和弹力做功，动能、重力势能和弹性势能三者发生相互转化，机械能守恒。

【拓展】竖直弹簧振子与水平弹簧振子的振动同为简谐运动，周期相同，区别在于它们的平衡位置不同。教学中可让学生类比思考，如果给水平弹簧振子加一个水平向右的恒力F作用，那么，它做简谐运动的平衡位置必右移同样的方法，也可以证明放在光滑斜面上的弹簧振子也做简谐运动。

【总结】简谐运动是物体在平衡位置附近所做的来回往复的周期性运动，它产生的根源是：运动物体一旦偏离平衡位置，就受到一个F=-kx的回复力的作用。简谐运动的x-t、v-t、a-t图像均为正弦函数图像，只是初相不同。简谐运动可以是直线运动，也可以是曲线运动。弹簧振子和单摆在振动过程中动能与势能发生相互转化，而机械能守恒。

【延伸】课后，教师还可以让学生寻找各种实例交流探讨，诸如漂浮在水中的密度计的上下振动、用绝缘细线悬挂的带电小球在电场或磁场中的摆动，在不计阻力的情况下，它们是不是做简谐运动，机械能是否守恒等。

三、串链——融通知识结构

如果说初探简谐运动的位移图像是在海滩上拾到了一个美丽的贝壳，那么，接下来对简谐运动的运动学特征、动力学特征、能量关系、周期公式的研究就是在贝壳中采撷到了闪光的珍珠。而生活、生产中的各种机械运动非常丰富，在学习简谐运动之前，我们早已重点研究了匀变速直线运动、平抛运动、匀速圆周运动等典型的机械运动。此时，师生格物致理、追本溯源，用“运动与相互作用”观、能量观将它们串线，即可使整个动力学知识形成一个有机、连贯的整体，成为一串美妙绝伦的项链。学生毫不费力就能拎起，然后在玩赏中将知识内化并迁移运用。

表1所示为五种典型运动的“运动与相互作用”关系，这五种典型的机械运动贯穿于物理学的始终，由易到难、由浅入深，将“运动与相互作用”观念层层展开。沿着这条主线，学生对运动和受力的认识会越来越深刻，理解也越来越透彻。而学好这五种典型运动的处理方法后，不管情境如何变化，问题都能迎刃而解。

表1 五种典型运动的“运动与相互作用”关系

【想象1】假想地球是一个密度均匀的球体，质量为M，半径为R，如果我们可以沿直径在地球上打一个洞，小球m在洞内无阻力运动且不被熔化（如图3所示）。今从洞口自由释放小球，小球将做什么运动？小球回到出发点需要多少时间？

图3 小球在地洞中的简谐运动

【探析】小球在洞中运动时仅受万有引力作用，此时万有引力定律公式中的地球的质量仅为图中阴影部分对应的质量。

这里，万有引力F的方向与位移x的方向相反，说明小球在洞内做简谐运动。

【想象2】假如有一艘飞船紧贴地球表面与小球从同一地点同时出发，飞船与小球谁先回到出发点？

【探析】飞船紧贴地球表面以第一宇宙速

而如果忽略地球自转，有GM=R2g

则它们的周期公式也可表述为

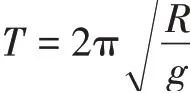
这样，就得到了一个非常有趣的结论：两者运动的周期相同，亦即当飞船和小球同时同地沿不同路径出发，它们却能同时回到出发点。这也从本质上揭示了物理规律的奇妙。

这两个能激活学生想象的问题，将简谐运动和匀速圆周运动完美融合，从万有引力定律出发勾起联想，让人产生超凡脱俗、顿悟宇宙深邃奥秘的心境，体验神与物游、情景交融、天人合一的心醉神迷的愉悦。学生在问题导航、体悟引路后即可展开思维翅膀，腾飞创新梦想。

【体悟】在水平气垫导轨上，将一轻弹簧的两端分别与质量为m1和m2的两个滑块相连接，开始时保持静止。现给左侧的滑块一个冲量后，它瞬时获得水平向右的初速度v0，以此刻为计时零点。体悟一下：两个滑块将如何运动？画出它们运动的v-t图像。

为达到良好的探究体悟效果，师生可以根据两个滑块的质量m1和m2的大小关系，分三种情况进行探究：（1）m1=m2；（2）m1＞m2；（3）m1＜m2。

【探析】两个滑块与弹簧组成的系统在气垫导轨上运动，气垫导轨可视为光滑水平面，因此这是动量守恒定律应用中的一个典型模型。由于很多学生对其本质还理解不透，教师不妨换个角度，从简谐运动层面来帮助他们进一步领悟。两个滑块与弹簧组成的系统获得水平向右的动量后，系统的质心将在气垫导轨上以的速度向右匀速运动，而两个滑块则分别相对质心做周期相同的简谐运动。

如果要直观分析的话，可以设计一组数据来完成，如用天平称出两个滑块的质量分别为m1=1kg和m2=2kg，假设初速度v0=3m/s，于是，可以画出如图4所示的v-t图像。

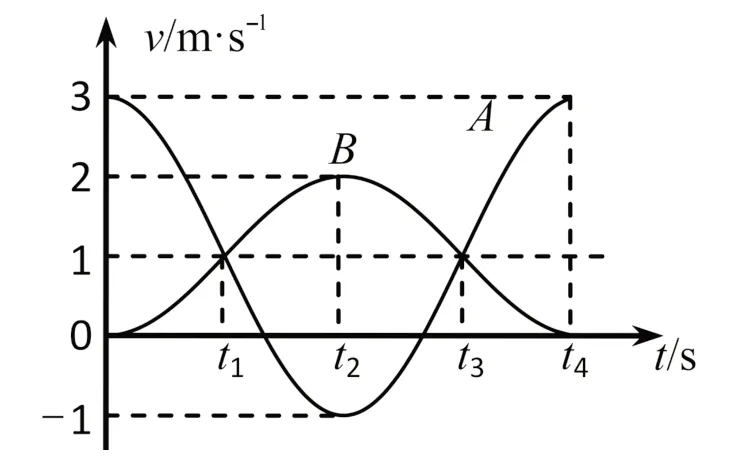
图4 夹弹簧模型的简谐运动

对于质量m1=m2和m1＞m2的两种情形，现象更加清晰明了，学生可进行“自主·合作·探究”学习，以增强体悟的效果。

这个相互作用物体一起做简谐运动的模型将动量守恒、能量守恒与弹簧振子的振动高度融合，学生在动量学习中初次接触时容易认识不清，现在再让他们亲历上述探究历程，必能深化其认识。教师如果能让学生经常从不同角度去亲身体悟、主动建构，则不仅能增强其学习乐趣，提高其学习热情，破解高分低能的难题，收到减负提质的效果，而且能帮助学生理解科学思维的精髓，掌握科学探究的方法，涵养科学精神，优化认知建构，使学生终身受益。

苏轼有一首充满禅意的《观潮》诗：“庐山烟雨浙江潮，未至千般恨不消。到得还来别无事，庐山烟雨浙江潮。”知识就如同这首诗的首句“庐山烟雨浙江潮”，如果教师没有引导学生对简谐运动的内容进行大单元的整合建构，那知识就只能是吸引学生去观赏的两个景点，但教师匠心独运，指导学生从运动学特征、动力学特征、能量关系三大视角，通过问题解悟、实践体悟、想象了悟的立体路径，进行充满好奇的探索学习后，学生的体悟就是第四句的“庐山烟雨浙江潮”，那是由外而内的明心彻悟，是“看山是山、看水是水”的第三重澄明境界，是超越了知识表象，而经由知识的运用、贯通和创新后生长的智慧。

从物理的视角看，“庐山烟雨浙江潮”自是人世间曼妙的风景，但不论是风霜雪雨、潮起潮落、云卷云舒，都有其内在的变化规律，它们无非是物质在不同温度、不同受力下所呈现的运动样态，虽千姿百态、风情万种，却大道至简、有章可循。当师生以大单元串链的方式去揭秘其间的奥妙时，那“珠围翠绕”的光华就能绽放眼前，并在心中建构起美轮美奂的知识结构，这也正是转识成智的精妙所在。此时，学生收获的是思维的提升、能力的发展和心智的成长，更进一步，则可实现化知识为能力、转情意为德性、变传承为创新的价值追寻。□◢