面积测量与计算中的“眼光”

□ 郜舒竹 罗玉晓

长期以来，小学数学有关“面积”的课程设计与教学，重视公式的推导、记忆和应用，相对忽视对图形之间的关系、公式的意义以及公式与公式之间关系的认知，导致记忆和计算成为数学学习的主要活动。因此学生会形成“离开公式看不出、没有数据算不出”的公式固着思维，缺失了多元的眼光、灵活的思维和丰富的表达。

事实上，任何公式都是规律或关系的表征形式，小学阶段中和面积测量与计算过程相关的认知活动不仅是套用公式的计算，更应重视对图形及其关系的观察和规律的发现，比如“从一看几”的迭代过程、“从异看同”的比较过程、“从给定看确定”的推理过程以及“从变化看规律”的发现过程。凡此都应当成为教科书编修以及教学设计中需要重视的课程内容。

一、从一看几

小学数学课程“图形与几何”领域中的“量（音：liàng，下同）”主要指长度、面积和体积（容积），这样的量具有“连续（Continuous）”和“广延（Extension）”的属性。连续是相对于“离散（Discrete）”而言的，离散的对象是“个体（Individual）”，没有共同边界，容易区分彼此，每一个个体可以自然地成为计数单位，因此是可以“数（音：shǔ）”的。而连续是“实体（Entity）”的属性，相邻部分具有共同边界，难以区分整体中的不同部分，更难以确定计数单位，因此不易像离散量那样计数。

广延是相对于“强度（Intension）”而言的，广延和强度都是实体具有的属性。比如，两杯热水倒在同一容器中，水的总容量成为原来两杯水容量的和，具有空间意义的“可加性”与“可分性”，属于广延量；水的温度则不同，合并后的水温不可能是原来水温的和，不具备广延量的可加性，只有强弱程度的差异。因此把类似于温度这样的量叫“强度量（Intensive Quantity）”，以区别于容量这样的“广延量（Extensive Quantity）”［1］。

广延性使得同样的量出现差异，因而产生比较与测量的需求；连续性导致离散量中计数的经验难以实施，导致测量的困难。按照德国哲学家、数学家莱布尼茨（Gottfried Wilhelm Leibniz，1646—1716）的说法：“（广延）量是某实体整体和部分共有的一种性质……测量是与单位的比较过程。”［2］英国哲学家、数学家罗素（Bertrand Arthur William Russell，1872—1970）对于量的认识与莱布尼兹有所不同，认为不应把量视为客观对象固有的内在性质，而是与人的认知相关联的：“量是人通过比较对关系的把握……孤立地看一个量，我们无法发现量的任何性质。”［3］按照罗素的观点，对量及其性质的认识是人在比较的活动中发现并建构的，这与奥地利-捷克物理学家、心理学家和哲学家马赫（Ernst Mach，1838—1916）的观点一致：测量是对两个同类量相等与不等关系的比较［4］。

比较的过程，自然产生并形成“等于、大于、小于”的顺序关系。为了使顺序关系更加清晰，就需要明晰“是多少、多多少、少多少”这样的问题，因此产生了对量的差异进行描述的需要，也就是对“量”赋予“数”的名称并建立顺序。实现这一过程的前提是将量与数建立对应关系［5］，简单说就是“知一”和“求几”。“知一”指的是确定单位，“求几”就是在“知一”的基础上，给相应的量赋予数的名称“几”。有了“几”这样的名称，同类量之间就具有了结构性的关系，具体表现为“一”和“几”的关系。因此面积测量过程需要经历的活动为：选择并确定面积单位以及与面积单位的比较，也就是“知一求几”或“从一看几”。这样的过程与线段长度的线性测量差异巨大，具有反直觉特征，蕴含着丰富的思维活动。面积测量过程不仅是承上启下的知识习得过程，同时是经历概念转变的思维发展过程。因此“从一看几”是面积测量过程中不可或缺的认知活动［6］。

二、从异看同

二维平面图形与一维直线的一个区别是存在“形异量等”的情况，即两个形状不同的图形可能面积相等。严格讲这样形异量等的两个图形并不是完全“相等（Equality）”的关系，正如“2+3”与“1+4”并不相同，而是诸多不同中某一属性具有共性，数学中通常用“等价（Equivalence）”表达这种异中之同的关系。对于两个分数，二者的读法、写法和意义均不相同，仅在所表达量的结果方面具有共性，因此二者的关系是等价关系。

“等价”表达的是两个不同对象之间的关系。人们为了某种目的或需求，忽略二者的相异之处，仅关注其异中之同，如果这样的共同点存在，就将不同对象视为在这一相同点上具有等价关系［7］。“2+3”与“1+4”等价，源于二者运算结果相同等价，基于所表达量相同。又如两条直线相互平行，这时二者的空间位置不同，它们是两条不同的直线，但如果想象某物沿着这两条直线运动，会发现运动方向一致（如图1）。因此“平行”作为两条直线的关系，可以看作方向意义上的等价关系。概括地说，所谓等价实质是“从异看同”的眼光。

图1 平行与等价示意图

凡平面图形都具有“形”与“量（面积）”的双重属性，根据二者的异同，可以将两个平面图形之间的关系概括为四种类型：形同量等、形同量异、形异量等和形异量异。其中的“形同量等”指的是形状与大小完全一样的“全等”关系；“形同量异”关注的是形状相同的“相似”关系，全等可以看作是相似关系的特例；“形异量等”既不同于全等关系，也不同于相似关系，指形状不同但面积相等。

图2中大长方形由“甲、乙、丙、丁”四个长方形组成，其中长方形丙的对角线分出的两个三角形“Ⅰ”和“Ⅱ”是全等关系；同样，长方形丁的对角线分出的两个三角形“Ⅲ”和“Ⅳ”也是全等关系。三角形“Ⅰ”和“Ⅱ”之一，与“Ⅲ”和“Ⅳ”之一是相似关系。而长方形甲和乙形状不同，但面积相等，因此甲和乙既不是全等关系，也不是相似关系，属于形异量等的等价关系。数学中的等价关系一般要求符合以下三个条件。

图2 图形等价关系示意图

●自身性：自己与自己等价。

●对称性：如果A与B等价，那么B与A等价。

●传递性：如果A与B等价，并且B与C等价，那么A与C等价。

平面图形的全等关系、相似关系以及形异量等的关系，均符合这三个条件，因此这三种关系都可以视为等价关系，区别在于，“从异看同”的着眼点和其他两者不同。相似（包括全等）关系是将形状这一“质”的因素作为关注点，形异量等的等价关系则忽略形状，仅关注“量（面积）”的属性。

诸如此类的等价关系都会在图形比较过程中出现。引导学生用“从异看同”的眼光观察、思考、表达这样的关系，就成为面积测量过程中必要的认知活动，以使学生在“从异看同”的过程中体会同中求异和异中求同的方法论。

三、从给定看确定

沿袭演绎推理的传统，数学课程内容中习惯采用“从给定到确定”的推理形式。“给定”与“确定”对应的英文均为“Given”，在推理中使用这一术语时，默认的意义是表达某对象“存在（Existence）”并且“唯一（Uniqueness）”［8］。比如：如果平面上给定两个不同位置的点，那么这两点之间存在唯一的直线；如果给定三角形三条边的长度，那么这个三角形的形状和大小随之确定，这样的性质也叫三角形的稳定性；如果给定一个正方形的周长，那么这个正方形的面积随之确定。但长方形的周长与面积就不具备这样的关系，给定长方形的周长，其面积存在，但未必唯一。如图3中两个长方形的周长均为14cm，二者面积则不等。

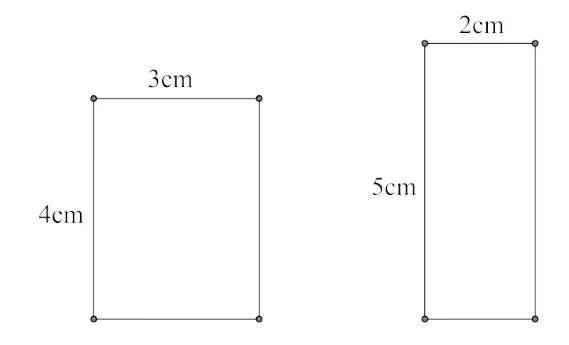
图3 周长相等，面积不等示意图

作为条件的“给定”实质是假定，未必是真实的，是设想了一个推理的前提，目的是实施从给定到确定的推理。因此，从给定到确定建立了一种从原因到结果的因果关系，数学中的命题或公式是这种因果关系的表征形式。对长方形来说，如果仅给定长或宽之一，无法使得面积确定，需要同时给定长和宽的长度，此时才可以感觉到这个长方形的形状和大小存在并且唯一，也就是长方形的面积是因长和宽同时给定而确定的，这样“双因一果”的关系可以用以下语言表述。

关系1：如果长方形的长和宽同时给定，那么这个长方形及其面积随之确定。

这样的关系显示出“长方形的面积=长×宽”实质是人为建构的，即用长方形的长和宽人为规定出长方形的面积，规定的依据正是从给定到确定的因果推理。数学与科学中许多概念都具有这种从给定到确定的人为规定特征。比如匀速运动，如果同时给定时间和路程，那么运动的快慢就随之确定，因此就用路程与时间这两个异类量之比，人为建构出“速度”这一概念，将运动快慢这一质的属性量化，成为沟通路程与时间两个广延量关系的强度量。

长方形的关系1可以利用“尺规作图”过程直观地感受。给定两条相互垂直的线段，这里的给定意味着两条线段的相对位置、夹角以及长度唯一确定。

图4中实际已经给定了长方形的三个顶点A、B、C，如果第四个顶点存在并且唯一，那么长方形及其面积就随之确定。用圆规和直尺作出第四个顶点的过程，可以显示出第四个顶点的确定性。具体做法如下。

图4 给定长和宽示意图

第（1）步：用圆规截取线段AB的长度为半径，以点C为圆心作圆，此时圆上每一个点到点C的距离都等于线段AB的长度，因此第四个顶点的位置应当在这个圆周上。（如图5）

图5 尺规做图（1）

第（2）步：用圆规截取线段BC的长度为半径，以点A为圆心作圆，这个圆上每个点到点A的距离都等于线段BC的长度。第四个顶点应当同时位于两个圆上，因此两个圆所形成的交点D就成为长方形的第四个顶点。用直尺分别连接AD与CD，构造出唯一确定的长方形ABCD。（如图6）

图6 尺规做图（2）

综上，“长方形的面积=长×宽”这一公式的意义并不限于计算，实质反映的是长方形边的长度与面积从给定到确定的因果关系。值得注意的是，这一关系具有单向的特点，即“如果给定长和宽，那么长方形及其面积随之确定”。但反过来的关系并不成立，如果给定长方形的面积，那么这个长方形的长和宽并不能唯一确定。这一点与正方形不同，如果给定一个正方形的面积，那么这个正方形的边长就随之确定。

“从给定看确定”是数学中广泛使用的推理形式，自然应当成为在数学学习过程中逐步形成并提高的能力，需要在教科书编修以及教学中有所体现。特别是要将尺规作图融入到这样的认知过程中，让学生有机会在尺规作图的具身活动中体会这样的推理形式，让尺规成为认知的工具，让作图成为认知的具身活动。

四、从变化看规律

这里的“规律（Pattern）”指的是运动与变化过程中相对稳定的关系［9］。用动态的眼光看，长方形面积与长和宽表现为相互关联的协变关系［10］。举例来说，如果将一张长方形纸沿着长所在边对折，实际上宽不变，长缩短为原来的二分之一，这时长方形面积同时也缩小为原来的二分之一。（如图7）

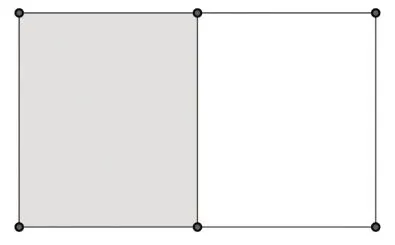
图7 折纸示意图（1）

如果继续沿着宽对折，得到的小长方形面积就成为二分之一的二分之一，即四分之一。（如图8）

图8 折纸示意图（2）

同样如果长方形的长扩大为原来的2倍，宽不变，那么长方形面积也随之扩大为2倍；如果长和宽同时扩大为原来的2倍，那么面积则扩大为原来的4倍。因此可以知道，长方形的面积与长（或宽）具有稳定的正比例关系，表述如下。

关系2：长方形面积与长（或宽）的长度成正比例。

这样的正比例关系在人们的日常经验中普遍存在。比如，如果把墩布擦地板的过程看作平移运动，把擦过的地面（长方形）的面积视为结果，这个结果由墩布的宽度和平移运动的距离两个因素决定。

如果给定墩布宽度，那么擦过地面的面积与平移运动的距离成正比例。同样，如果给定运动距离，那么擦过地面的面积与墩布宽度成正比例。

像这样用擦地的过程认识面积的方法,是将“面”视为“线”运动过程中所产生的轨迹，是用动态的眼光看待图形，这样的方法通常用于连续量的认识与测量，叫作面积的“动态度量（Dynamic Measurement，简写为DYME）”［11］。相对于静态的眼光，动态度量不是将平面区域看作面积单位填充的“容器（Container）”，而是运动“路径（Path）”中轨迹的生成或积累［12］。动态度量的眼光对于数学的发现与发明意义重大，伟大的科学家、数学家牛顿（Isaac Newton，1643—1727）发明的“流数法”是微积分诞生的一个标志。论及流数法的基本原理，牛顿在其名著《流数法与无穷级数》的前言中说：“可以把数学中的量看作是连续运动产生出来的。”［13］可以说，牛顿发明的微积分实际是以动态度量为思想基础的［14］。

动态的眼光使得长方形面积与长和宽的因果关系，与行程问题中路程、时间和速度之间的关系具有了思想的一致性。14世纪法国哲学家、科学家尼克尔·奥里斯姆（Nicole Oresme，约1320—1382），在研究如何将运动的快慢进行量化的时候，就是用长方形作为模型表达匀速运动各个量之间的关系［15］［16］。“长方形的面积=长×宽”与“路程=速度×时间”思想的一致性，可以进一步拓展到诸如工程问题、购物问题、利率问题、浓度问题等问题中（如表1）。

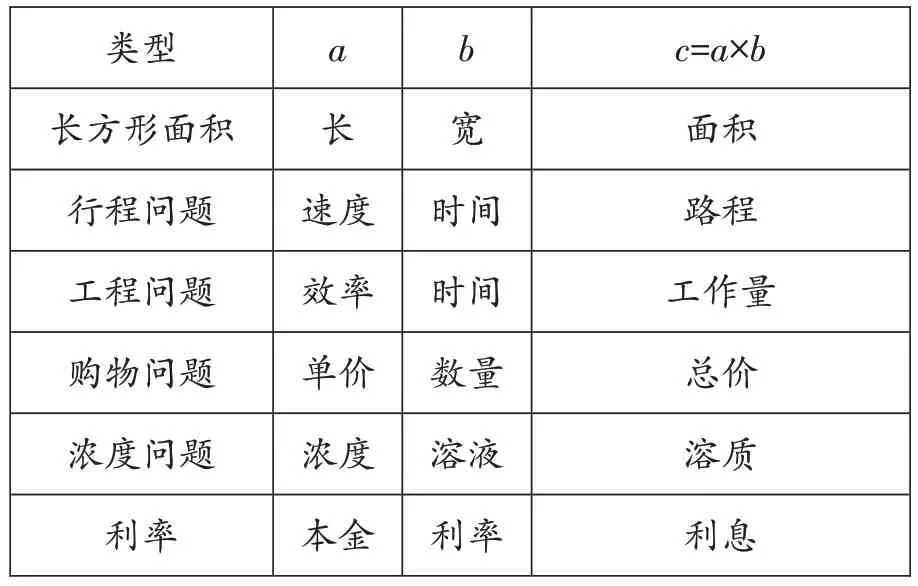
表1 数量关系一览表

其中的因数a与因数b以及乘积c，都体现出长方形中长、宽与面积双因一果的关系，即“c=a×b”表达的是以a与b作为原因产生结果c的过程，遵循的规律是：

●给定a与b，则c随之确定。

●给定a，则b与c成正比例。

●给定b，则a与c成正比例。

法国著名的数学教育家杰勒德·怀尔格（Gerard Vergnaud，1933—2021），把诸如此类乘法运算所表达关系在思维中的表现，称作“乘法概念域（Multiplicative Conceptual Field，简写为MCF）”［17］。综上可知，乘法概念域中的思维过程至少应当包括“从给定到确定”以及“从变化看规律”的推理过程。

总之，小学数学课程中面积测量与计算的内容具有丰富的育人功能。因此，本文从认知过程中提取出“从一看几、从异看同、从给定看确定、从变化看规律”的认知活动。这些活动着眼于量以及量之间关系，弱化套用公式的数与计算，将数字符号及其关系降为次要地位。美国的帕特里克·汤普森把这样的认知活动称为“量推理（Quantitative Reasoning）”［18］。像这样针对量以及量之间关系的量推理，是学生在数学学习中需要逐步提升的认知能力，也是今后数学学习的基础，因此应当成为教科书以及教学设计需要重视的课程内容。