面向语音增强的聚焦自适应波束形成方法

陈鹏,李洋洋,高婧洁,王威

(长安大学信息工程学院,710064,西安)

语音信号具有一定的带宽,且往往被宽带干扰和噪声遮蔽,难以被直接提取[1],一般需要自适应宽带波束形成技术对阵列观测信号进行处理,以抑制干扰和噪声,从而提高其信号质量[2]。

宽带自适应波束形成技术从实现方式来看,主要可以分为时域有限冲击响应(FIR)技术[3]以及频域离散傅里叶变换(DFT)技术[4]。基于时域FIR技术的波束形成方法的主要缺点是计算复杂度较高[5],其所需的FIR滤波器的阶数会随着带宽的增加而急剧增大[6],难以在便携式、可穿戴设备等计算资源不充足场景中得到广泛应用[7]。

基于频域DFT的自适应波束形成技术,首先将宽带接收信号进行离散傅里叶变换,并划分子带,从而在频域子带内进行处理。频域DFT的自适应宽带波束形成根据频域子带数据的处理方式的不同,可以分为两类。第一类为非相干子空间类方法(incoherent subspace method,ISM)[8],其主要原理为在各个子带内进行窄带自适应波束形成从而合成频域输出信号。然而,ISM方法在子带内只利用了宽带信号的部分频点信息,导致其对误差较为敏感,且无法处理相关信源,总体性能较低[9]。第二类为相干子空间类方法(coherent subspace method,CSM)[10],其基于频域聚焦的思想,能够充分地利用宽带信号的带宽信息,从而提高波束形成器的稳健性。CSM通过构造频域聚焦矩阵,使不同子带内的窄带信号在参考频率上实现聚焦,从而将宽带问题转换为窄带问题进行处理,以较低计算复杂度得到宽带波束输出。

从20世纪90年代至今,学者们提出了许多经典的聚焦矩阵构造方法[11],例如旋转信号子空间(RSS)变换法、信号子空间变换法(SST)、双边相关变换(TCT)[12]、单约束的阵列流形聚焦(UCAMF)[13]。然而,上述聚焦矩阵的计算是建立在所有入射信号的DOA都精确已知的条件下的,如果假设的DOA与实际DOA存在误差时,聚焦方法的性能将会急剧下降。针对该问题,Bucris等[14]提出了贝叶斯聚焦变换(Bayesian focusing transform,BFT),其假设入射信号的DOA服从高斯分布,尽管在一定的范围内可以减小角度失配对波束形成性能的影响,但是该方法实现前提要求为所有信号入射角或其概率分布参数确定已知[15]。此外,该方法在频域聚焦还是基于传统的采样协方差矩阵求逆[16](sample covariance matrix inversion,SMI)或对角加载方法(diagonal loading,DL)[17],对导向矢量误差较为敏感。因此,现有宽带聚焦波束形成方法仍然具有和采样协方差求逆方法一样的缺点,即相关参数选取与实际阵列接收数据存在失配时,聚焦误差会急剧增大,从而造成导向矢量失配,严重降低自适应波束形成器的性能,甚至会出现在期望信号方向形成零陷的“自消”现象[18-20]。

针对上述问题,本文在信号入射角的概率分布参数未知的情况下,通过预估参考频率处空间谱得到所有信号大致的角度和功率信息,从而将空间谱拟合为信号入射角的概率分布函数,继而提出新的聚焦变换方法。然后,本文将干扰加噪声协方差矩阵(interference-plus-noise covariance matrix,INCM)重构的思想[21-25],与所提频域聚焦变换结合,提出了一种频域聚焦的重构波束形成方法。数值仿真验证了所提波束形成器能够在信号入射角未知时,有效地预估入射角的概率分布函数并将宽带数据聚焦到参考频点处,最终高效地抑制宽带干扰。

1 宽带信号模型

考虑M个传感器组成的均匀线列阵接收来自空间的宽带信号和噪声的时域数据为

X(t)=[x1(t),x2(t),…,xM(t)]T

(1)

式中:xm(t)表示第m个阵元接收到的时域数据,其与噪声不相关。那么将X(t)内各个阵元S0(f)的时域数据进行快速傅里叶变换,得到频率域的阵列观测数据X(f)可表示为

X(f)=

(2)

式中:S0(f)和Sq(f)分别表示期望信号和第q个干扰的频域数据;a(θ0,f)和a(θq,f)分别表示对应的导向矢量;N(f)表示噪声频谱数据。一般地,在进行阵列信号处理前,应当首先选择感兴趣的接收信号的带宽范围为[fL,fH],其中fL为信号带宽下限,fH为信号带宽上限,傅里叶变换后在X(f)带宽范围内共有Nf个离散频点,将[fL,fH]带宽内的频点平分为I个频率集,每个频率集内有J个离散频点,则Nf=IJ。θ0和θq分别为信号与干扰的入射角,定义为与直线阵法线方向的夹角。

对于所有接收信号,假设其在频率fi下的导向矢量集合为A(ΘS,fi)=[a(θ0,fi),…,a(θq,fi)],那么第i个频率集内的聚焦矩阵必须满足

A(ΘS,fr)=T(fi)A(ΘS,fi)

(3)

式中:ΘS表示所有信号DOA的集合,第i个频段和参考频点的导向矢量是已知的。那么,可以采用最小均方误差(MMSE)准则,构造求解问题为

(4)

(5)

式中:e(θ)为聚焦后的导向矢量和参考频点导向矢量的误差,可以表示为

e(θ)=T(fi)ρ(θ)a(θ,fi)-ρ(θ)a(θ,fr)

(6)

式中各信号DOA都服从等方差高斯分布N(θ,σ2),则全角度域的DOA的存在概率服从

(7)

实际计算中,如果离散角数足够多且满足采样条件(离散角数远远大于频点集数),那么聚焦矩阵可以在角度域内近似为

(8)

式中:Γ为对角阵,其对角线元素为离散角对应的概率值;(·)+表示伪逆算子。

2 频域聚焦重构波束形成

由式(6)、(7)可知,某一角度处的聚焦误差与该角度存在的信号概率大小成负相关。式(7)中假设在各信号等概率时难以保证所有信号的聚焦总体误差最小。因此,本文提出自适应聚焦变换(adaptive focusing transform,AFT)的概念,在保证期望信号方向的聚焦误差足够小的同时,根据各个干扰的功率大小自适应地进行聚焦,从而将更多的聚焦资源倾斜于强干扰的聚焦和抑制中。

2.1 所提频域聚焦方法

在选取参考频点fr后,将其所在的频率集对应的所有阵元数据定义为Xr(f)。此时,可以计算参考频率集的采样协方差矩阵为

(9)

此时参考频点fr所对应的Capon空间谱可以被计算为

(10)

峰值提取可能会出现误差,即提取的峰值数与实际的入射信号数不同,也无法保证期望信号能够被正确地提取出。因此,根据先验条件,将期望信号的入射角扩展为一个期望信号扇区Θ0=[θ0-B/2,θ0+B/2],以囊括所有可能的角度误差,B为区间宽度。将Θ0内的Capon谱归一化,并取Capon空间谱内的最大值,从而提高期望信号在所有信号与噪声中的比重。修正后的Capon谱为

(11)

那么,概率密度函数ρ2(θ)可以被重构为归一化的修正Capon谱,即

(12)

(13)

此时非信号区域内的概率密度仍远大于0,这与实际情况不符(非信号区域内的信号存在概率应当非常小)。因此,式(12)的概率密度函数可以被重写为

(14)

根据式(8),对角阵Γ可以被估计为

(15)

式中:diag(·)表示向量对角化。此时第i个频率集的自适应聚焦矩阵就可以被写为

(16)

那么第i个频率集内的频域数据经过聚焦后为

(17)

此时该频率集的聚焦样本协方差矩阵为

(18)

将所有的频率集对应的样本协方差矩阵进行综合后,可以得到总体聚焦样本协方差矩阵为

(19)

2.2 波束形成器设计

在得到所有的自适应聚焦矩阵和总体聚焦样本协方差矩阵后,所有频率集的频域数据都被聚焦到了参考频点,因此只需要在参考频点处设计自适应波束形成器即可。

式(19)中的总体聚焦样本协方差矩阵包含期望信号成分,而聚焦过程不可避免地会产生一定的误差,可能会导致期望信号“自消”的现象[5],严重影响波束形成器的性能。因此,可以利用总体聚焦样本协方差矩阵重构第i个频率集下的干扰加噪声协方差矩阵,具体可以写为

(20)

(21)

聚焦后的干扰加噪声协方差矩阵可以写为

(22)

将式(21)代入式(22)中,可以得到

(23)

在实际应用中,一般无法精确得到期望信号的导向矢量,通常需要进行估算或修正。针对这个问题,本文将利用重构协方差矩阵的思想,首先对期望信号协方差矩阵进行重构,表达式为

(24)

式中:Ls为期望信号扇区Θ0内离散角数。在此基础上,取最大特征值对应的特征向量作为期望信号导向矢量,表达式为

(25)

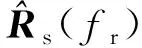
(26)

此时,自适应聚焦宽带波束形成器的输出频域信号可以写为

(27)

(28)

最后通过采用逆傅里叶变换,自适应宽带聚焦波束形成器输出的时域信号为

(29)

式中:IDFT{·}表示逆傅里叶变换算子。

由频域聚焦重构波束形成方法的过程可知,方法的计算复杂度主要来源于两个部分:第一部分是聚焦矩阵估计,对于所有的频率集,其复杂度为O(M3I),I为所有频率集数;第二部分来源于干扰加噪声协方差矩阵的重建和导向矢量的估计过程,其中干扰加噪声协方差矩阵重建的复杂度为O(M2Li+n);而DSCM重建的复杂度为O(M2Ls);特征分解在SV估计中的复杂度为O(M3)。一般而言,I≥1且Li+n≫Ls。因此,本文提出方法的总计算复杂度为O(max{M3I,M2Li+n})。文献[14]中没有给出计算复杂度分析,但其提出的BFT对焦加载波束形成方法无需进行协方差矩阵重构,因此计算复杂度主要依赖于聚焦矩阵估计过程,其复杂度同样为O(M3I)。文献[5]的计算复杂度可以写为O(max((MJ)2IDL,(MJ)2DLs)),其中,J为滤波器阶数,通常取15,I为频率集数,Ls和L为期望信号扇区及其补扇区内的离散角数,D为二次采样数,通常取D=179。通过对比可知,文献[14]所提方法具有最低的计算复杂度,所提方法与文献[14]相比计算复杂度提升不多,而文献[5]的计算复杂度远远高于所提方法。

3 数值仿真

数值仿真实验中,考虑由10个全向传感器组成的均匀线阵列(uniform linear array,ULA)。假设空气中的声传播速度c=340 m/s。所有信号的频率范围是2 000～3 000 Hz(需要指出的是,国际制定的数字电话机的通信标准是300～3 400 Hz,本算例中仅对其中部分频段做出仿真,但是结果具有普适性,如需覆盖所有频段仅需提升频带数即可),相邻两个传感器之间的距离为最高频率(3 000 Hz)对应波长的一半,采样频率fs=12 500 Hz。期望信号是由带通滤波后的高斯噪声产生的,而且每个频率上的信号功率都是不同的,期望信号的入射角为15°。两个干扰为带宽范围内的线性调频信号,其中一个为30 dB的强干扰,其入射角为35°,线性调频率为5 000 Hz/s(升频率);另一个为10 dB的弱干扰,入射角为-25°,线性调频率为-5 000 Hz/s(降频率)。阵列噪声为高斯白噪声,功率为0 dB。式(14)中的聚焦参数为η=0.01,ξ=10-6。

3.1 聚焦误差

为了研究所提频域聚焦重构方法的性能,将宽带频率范围等分为10个窄带频带,并将聚焦频率设置为第5频带的中心频率fr=2 450 Hz,期望信号的功率值设定为20 dB。

图1展示了第1频带的导向矢量聚焦的均方误差随入射角的变化情况,其中,聚焦的均方误差可以计算为

(30)

可以看出,RSS聚焦方法的整体聚焦误差在10°以上,CSM方法的聚焦误差在期望信号和干扰方向上大致达到了10-2量级。BFT聚焦方法的聚焦误差也在3个信号的方向附近达到了10-3量级。然而,由于BFT方法设置为均匀聚焦,其在3个方向上的聚焦误差基本相同,不利于后续高功率信号的对准和干扰的抑制。由于采用了自适应的聚焦方式,AFT在-25°的低功率方向上将误差降低至10-3量级,而在期望信号和30 dB干扰方向上,聚焦误差仅为10-6量级。

图2展示了此时各个频带内的聚焦误差情况。由图2可以看出,BFT聚焦方法在3个信号入射角上的聚焦误差差距不大,且其在各个频带内的聚焦误差基本上维持在10-3量级。值得注意的是,图2中缺少了5号频带的聚焦误差,这是因为5号频带的中心频率为参考频率,5号频带可以直接进行波束形成处理而无需进行聚焦。AFT聚焦方法在弱干扰处的聚焦误差较高,从而将有限的“聚焦资源”分配给了功率较高的干扰和期望信号。此外,因为1号频带为低频段,聚焦误差在1号频带内最大,随着频率的升高以及靠近参考频率时,2～8号频带的聚焦误差显著减小。从9号频带开始,其与参考频率的差距开始成为聚焦误差的主要因素,聚焦误差开始升高。

3.2 波束响应图

虽然聚焦波束形成能够处理宽带信号,但从图2可知,不同频带的聚焦误差存在差异。因此,本小节将研究不同频带的聚焦对波束响应图的影响。为了独立展示聚焦和协方差矩阵重构对波束形成性能的影响,将AFT和BFT两种聚焦变换分别与稳健Capon波束形成器(robust capon beamformer,RCB)和重构估计波束形成器(reconstitution and Estimation beamformer,REB)相结合,从而在对比方法中除BFT-RCB外,还将BFT-REB作为另一个对比方法。值得说明的是,图1表明CSM和RSS聚焦方法显著劣于BFT方法,因此在后续的仿真中不再将CSM和RSS聚焦方法作为对比方法。

图3给出了1号频带的波束响应图,可以看出,最低频带对应的波束响应图中,BFT-RCB方法将主瓣移至了-90°方向,在真实的期望信号方向15°形成了一个-16 dB的旁瓣。由于AFT-REB和BFT-REB采用了重构技术,在15°形成了主瓣,并在多个干扰方向也形成了凹槽。

图4给出了4号频带的波束响应图,可以看出,由于其接近参考频率,聚焦误差显著降低,使得各个波束形成方法都能够将主瓣对准,然而BFT-RCB的主瓣稳健性是以牺牲干扰抑制能力为代价的。相较而言两个重构波束形成方法保留了较强的干扰抑制能力,且AFT-REB在大角度区域对噪声的抑制能力明显优于BFT-REB。

图5给出了最高频带的波束响应图,其与图4类似,AFT-REB与BFT-REB都能够较好地形成主瓣并抑制干扰。

3.3 输出信干噪比

本节给出了各个波束形成器的输出信干噪比情况。图6给出了入射角精确已知时,各波束形成器的输出信干噪比(signal-to-interference and noise-ratio,SINR)随输入信噪比(signal-to-noise-ratio,SNR)的变化情况,图6中的结果是200次独立的蒙特卡洛仿真的平均值。可以看出,尤其是在高SNR情况下,BFT-RCB的输出信干扰比与两个重构波束形成方法存在较大差距。AFT-REB的输出SINR一直略高于BFT-REB,这是由于AFT-REB有更灵活的频率聚焦能力,能够优先保障期望信号和强干扰处的聚焦,减小聚焦误差从而提高强干扰的抑制能力。

在实际应用中,一般难以准确知道信号入射角。因此假设所有信号存在3°的入射角误差,即假设的期望信号的入射角为18°,两个干扰的角度分别为-22°和38°。从图7可以看出,由于角误差的存在,聚焦的误差也不可避免,从而导致AFT-REB和BFT-REB的性能出现轻微的下降,由于角度误差的存在,BFT-RCB输出SINR随着信噪比的升高而急剧下降。

4 结 论

本文针对现有宽带聚焦波束形成方法在频率聚焦和波束形成时存在的问题,提出了频域聚焦的协方差矩阵重构波束形成方法,通过将接收信号空间谱拟合为入射角的概率密度函数,得到了各个频带所对应的聚焦矩阵。在此基础上,将原始宽带数据聚焦为窄带数据,并重构出了所有频带对应的干扰加噪声协方差矩阵和期望信号导向矢量,最终得到了聚焦数据所对应的加权向量。与其他聚焦波束形成方法相比,所提方法能够根据干扰的功率大小自适应地调整聚焦程度,从而提高了整体的波束形成性能。数值仿真证明,所提AFT-REB波束形成器能够有效地对期望信号进行接收的同时充分抑制宽带干扰。