弧齿锥齿轮复合传动误差设计与分析

苏进展,许鹏,刘镔,郭芳,杨羽

(长安大学道路施工技术与装备教育部重点实验室,710064,西安)

传动误差包括几何传动误差和承载传动误差,是影响螺旋锥齿轮动态特性、齿面接触质量和振动噪声的重要因素,其由弧齿锥齿轮的准共轭特性以及啮合刚度的周期性变化共同作用而产生的。随着高速直升机主减、新能源商用车的广泛使用,弧齿锥齿轮的高频噪声问题日益突出,已成为影响传动系统NVH的关键因素。弧齿锥齿轮的噪声与齿面的高阶谐波相关,而齿面几何形状则是由加工参数来确定的。

通常情况下,弧齿锥齿轮的设计是接触有限元法分析其啮合性能。侯祥颖等[1-2]提出了在不同载荷条件下考虑边缘接触的定量分析,通过对比有限元与TCA法分析下的传动误差,验证了有限元法可以较为精确的分析传动误差。传统Gleason螺旋锥齿轮设计和制造方法是基于非共轭齿面。在实际应用中,二阶抛物线传动误差降低了啮合质量对安装误差的敏感性,获得了较好的传动性能。Litvin等[3-5]提出了二阶抛物线型传动误差曲线,它可吸收齿轮副因制造安装误差而引起的线性误差,从而降低了齿轮系统运行过程中的振动与噪声。方宗德等[6]提出了基于抛物线型传动误差设计的高重合度弧齿锥齿轮,改善了弧齿锥齿轮传动系统的强度性能。刘光磊等[7-10]以局部综合法为基础,提出半变性法和泛变性法来优化抛物线型传动误差曲线,并提出了几何传动误差曲线的吻合度概念和对称度概念。

目前,满足二阶抛物线型传动误差设计的弧齿锥齿轮已经得到了广泛应用,但二阶抛物线型传动误差的加速度曲线在啮合转换点位置处产生的冲击会严重影响弧齿锥齿轮的啮合性能。为此,格里森公司Stadtfeld等[11]提出了形状类似于高阶抛物线的高阶传动误差曲线,该几何传动误差曲线啮合转换点位置处的夹角较二阶抛物线型传动误差曲线有着明显的增大。王培郁等[12]通过MRM齿面曲率修正方法设计了满足四阶抛物线型传动误差设计的Face-Milling弧齿锥齿轮,并对其啮合性能进行计算机模拟仿真。魏冰阳等[13]针对由变性法加工的弧齿锥齿轮,设计了四阶抛物线型传动误差曲线,并分析其啮合性能。苏进展等[14-15]针对基于变性法加工的弧齿锥齿轮,通过提高小轮加工参数中变性系数的阶数,设计了四阶传动误差和七阶传动误差,并进行啮合性能对比分析。曹雪梅等[16]提出一种基于共轭齿面修整的弧齿锥齿轮高阶传动误差设计,经过两次齿面修整实现高阶传动误差和齿面印痕的精确控制。牟彦铭等[17-20]提出了基于齿面曲率修整的高阶传动误差设计,有利于改善载荷分布。

近年来,美国格里森公司Stadtfeld博士[21]提出将几何传动误差设计为单齿啮合区是正弦函数,两侧为抛物线函数的方法,并通过试验验证了该方法能够有效减小锥齿轮副的高频噪声。由于商业秘密和国外技术封锁,其背后设计思想及加工方法仍处于猜测中。鉴于此,本文提出了弧齿锥齿轮复合传动误差设计,通过优化局部综合参数,获得几何传动误差对称和工作载荷下承载传动误差波动量最小的机床加工参数;在此基础上,进行复合传动误差设计,并根据逆TCA方法确定3段高阶变性系数,从而实现复合传动误差的磨齿加工;最后,进行几何啮合仿真、多载荷承载啮合仿真、齿面偏差及高阶频谱对比分析,验证该设计方法的有效性和可行性。

1 传动误差优化设计

几何传动误差对称性和承载传动误差波动量是影响齿轮啮合传动性能的关键因素。对称性是指传动误差曲线以设计参考点为对称中心,啮入、啮出部分具有相等的传动误差幅值、对称的曲线形状以及相同的啮合时间,从而保证传动平稳性和避免过早发生边缘接触。齿轮副在工作载荷下的承载传动误差最大值和最小值之差称为波动量,其值越小有越利于减小刚度激励,降低振动噪声。

弧齿锥齿轮传动误差的多目标优化模型通过优化变量、目标函数和约束条件来表示,其中优化变量如图1所示。

目标函数可表示为

(1)

约束条件可表示为

(2)

传动误差优化过程是一个不断地求解主动设计[18]、TCA、LTCA的迭代过程,设计变量和目标函数之间没有直接关联,即不能建立设计变量到目标函数的解析表达式,且存在多个局部最优解,因此传统的优化算法并不适用。本文采用遗传算法进行求解,具体步骤包括编码、初始种群生成、适应度评估和检测、选择、交叉和变异等操作。图2为优化流程图。

2 复合传动误差设计

图3为复合传动区内。在空载条件下,定义前、后齿对和当前齿对进行啮合转换时的交点分别为啮入转换点B和啮出转换点D,将小轮转角φB=φ1C-Tm/2、φD=φ1C+Tm/2带入TCA基本方程中,求得啮入转换点和啮出转换点的传动误差幅值δ2B和δ2D,其中Tm为啮合周期。图3中在单齿啮合区上为简谐函数,而在其余啮合区为抛物线函数。当简谐函数为正弦函数时,其传动误差BD段的表达式为

δ2=Amsin(ωm(φ1-φ10)-ωm0)+Am

(3)

式中:φ1为小轮啮合转角;圆频率ωm=2π/Tm;相位角ωm0=ωmTm/4;幅值Am=δ2B/2或者Am=δ2C/2。在啮入转换点B和啮出转换点D,当前齿对和前后齿对的传动误差曲线夹角均为180°,能够保证啮合转换的平稳过渡,不会产生换齿冲击。

左侧AB段抛物线的表达式为

(4)

式中:k为抛物线的阶次,取为偶数。该函数能够保证在传动误差在B处k-1阶连续可导。根据啮入点A的传动误差幅值,计算抛物线系数为

(5)

同理,右侧DE段抛物线的表达式为

(6)

抛物线系数为

(7)

因此,在整个完整啮合过程中(即单对齿从进入啮合到退出啮合)的传动误差表达式为

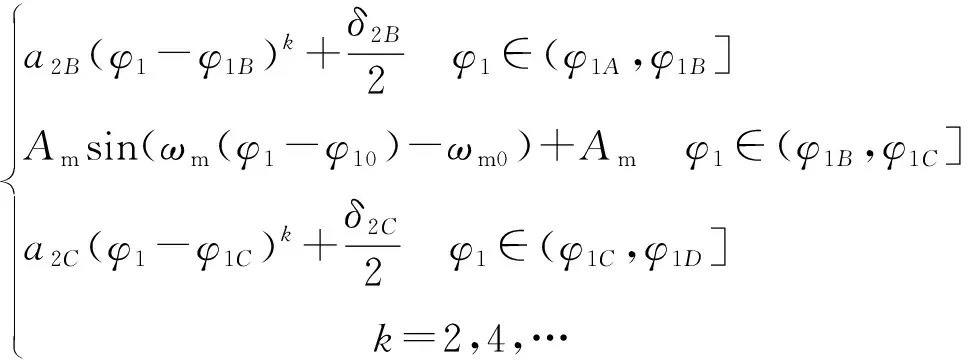
(8)

3 加工原理

根据预置的复合传动误差曲线,结合传动误差的定义,求得小轮啮合转角φ1所对应的大轮啮合转角为

(9)

式中:Z1和Z2分别为小轮和大轮的齿数;φ1C、φ2C分别为小、大轮的初始啮合转角。对于AB段抛物线传动误差,将小轮转角φ1∈(φ1A,φ1B]划分为n1-1等份,小轮啮合转角φ1i1=φ1A+((φ1B-φ1A)(i1-1))/(n1-1)(i1=1,2,…,n1),代入AB段表达式中,获得对应的大轮啮合转角φ2i1。对于BC段正弦函数的传动误差,将小轮转角φ1∈(φ1C,φ1D]划分为n2-1等份,φ1i2=φ1C+((φ1D-φ1C)(i2-1))/(n2-1)(i2=1,2,…,n2),代入BC段表达式中,获得对应的大轮转角φ2i2。对于DE段抛物线传动误差,将小轮转角φ1∈(φ1D,φ1E]划分为n3-1等份,φ1i3=φ1D+((φ1E-φ1D)(i3-1))/(n3-1)(i3=1,2,…,n3),代入DE段表达式,获得对应的大轮转角φ1i3。以小轮滚比为参数,采用逆轮齿接触分析的方法[14],计算出一系列的小轮瞬时滚比rai1、rai2、rai3和小轮摇台转角φc1i1、φc1i2、φc1i3,将其拟合成多项式表达

(10)

式中:N1、N2和N3分别为多项式的幂次;b10、b11、b12、b13、……、b1N1,b20、b21、b22、b23、……、b2N2,b30、b31、b32、b33、……、b3N3分别为传动误差啮入段AB、单齿啮合段BD和啮出段DE对应的高阶变性系数。当两侧抛物线阶次越高,表示从啮合转换点到啮出或啮入点之间越陡峭,幂次N1、N2和N3取较大值,可提高瞬时滚比的拟合精度。

综上,为了获得复合传动误差,小轮瞬时滚比在加工过程中是不断变化的,其表达式为

(11)

4 算 例

以一对弧齿锥齿轮副的工作面为例,表1为齿轮副几何参数,表2为参考点的局部综合参数,表3为齿轮副工作面的加工参数;所获得的对称传动误差在关键设计点A、B、C、D、E的小轮转角和传动误差幅值分别为-15.549 8°、-6.074 3°、-1.751 7°、9.577 8°、18.962 7°和-80.019 2″、-15.0″、0″、-15.0″、-79.213 2″,啮入点A和啮出点E相对于参考点C的啮合转角误差小于0.001°,传动误差幅值误差小于0.1″,达到较高的传动误差对称性要求。采用本文的设计方法,将单齿啮合区设计为正弦函数,各参数分别为ωm=23,ωm0=π,Am=-7.5″。

表1 齿轮副几何参数

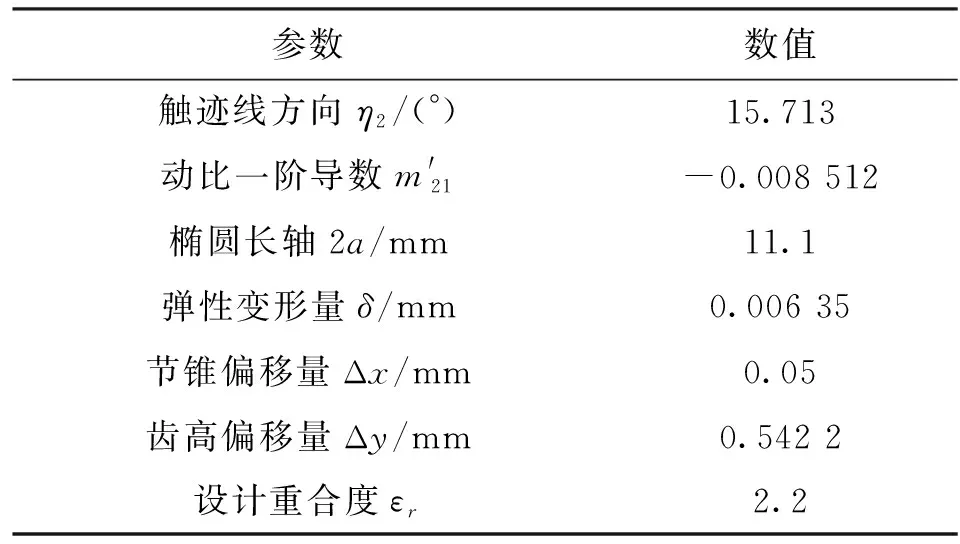
表2 参考点的局部综合参数

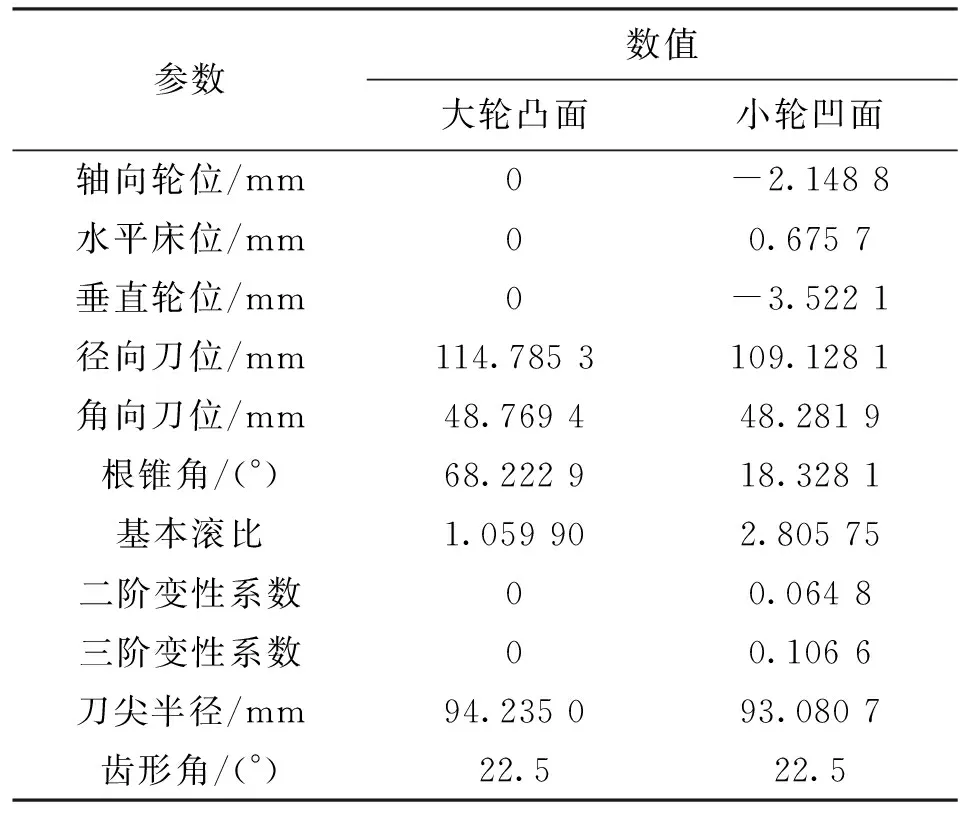
表3 齿轮副工作面加工参数

两侧抛物线系数k=2,4,…,反映了抛物线的陡峭程度,阶次越高对啮合性能影响不大,但不易通过高阶变性法实现加工,因此取k=2,a2B=a2D=-0.011 5。采用逆轮齿接触分析方法时[14],3个区间的离散等份均取n1=n2=n3=100,多项式的幂次取N1=N2=N3=5。参考典型遗传算法参数的设置范围,结合本文实际问题规模,经过多次试验后,确定遗传算法参数具体设置如下:种群大小50,进化代数100代,交叉概率0.5,变异概率0.1。在该组参数下能够取得较好的优化效果。

图4和图5分别为抛物线传动误差设计和复合传动误差设计的TCA结果。从图4和图5的传动误差曲线比较可知,复合传动误差在啮合转换点处的夹角等于180°,能够使前、后齿对平稳过渡,不会产生换齿冲击。

这两种设计方法的设计重合度、啮合转换点幅值、啮入点和啮出点幅值都十分接近,便于后续进行啮合性能对比。

图6为两种设计的瞬时滚比曲线。当多项式幂次取5阶时,能够取得较好的拟合效果,最大拟合误差不超过1.0×10-5。表4为复合传动误差的基本滚比和高阶变性系数,故而可在现有的螺旋锥齿轮数控磨齿机上加工(如格里森Phonic系列和Klingerberg C系数锥齿轮机床调整参数多项式的最高幂次均为6次)。

表4 高阶变性系数

图7为两种设计的齿面偏差比较,以抛物线传动误差设计为基准齿面,定义复合传动误差设计的小轮齿面沿着基准齿面法向方向的投影为齿面偏差,从图中可以看出最大偏差+81 μm出现在大端齿根处。在小端齿顶和大端齿根处出现正偏差,这是由于复合传动误差设计在从啮入点到啮入转换点以及从啮出点到啮出转换点这两段区域内的修形量较抛物线传动误差设计少,而在参考点中点附近则是相反的情况。

图8和图9分别为两种传动误差设计在多载荷下的承载传动误差曲线,大轮负载扭矩从上到下分别为5.0、100、200、300、400、500、600、700、800、900和1 000 N·m。图10为承载传动误差波动量随负载扭矩的变化曲线。承载传动误差曲线主要是几何传动误差曲线形状和不同载荷下实际重合度变化引起的轮齿综合变形的结果,从图8和图9可知,两种设计从低载到工作载荷传动误差的形状基本相同,幅值逐渐减小;当载荷大于工作载荷后承载传动误差形状发生改变且幅值逐渐增大。在工作载荷400 N·m附近,齿轮副实际重合由2齿对变换到3齿对同时接触承载。

图11为工作载荷为400 N·m时的承载传动误差,经过快速傅里叶变化后得到的前六阶频谱图。

从图11可以看出,采用复合传动误差设计的各阶频谱幅值于均小于抛物线传动误差设计,复合传动误差设计的频谱幅值的平均值为0.527″,而抛物线传动误差设计频谱平均值为0.658 2″,幅值平均水平下降了19.86%。分析各种载荷下的频率图可知,两种传动误差设计下的频谱幅值图变化规律与工作载荷基本一致,在此不再赘述。因此,复合传动误差设计有利于降低齿轮副的高频振动和噪声。

5 结 论

(1)对于复合传动误差设计,在轻载(小于最大载荷10%)的承载传动误差为简谐函数,其与几何传动误差在单齿啮合时的传动误差曲线基本一致,简谐函数的各阶导数均是连续函数,且啮合转换点处的夹角等于180°,啮合齿对转换平稳,改善换齿的加速度冲击。

(2)相比于抛物线传动误差设计,复合传动误差设计的多载荷承载传动误差波动量较小,故而减小齿轮副的刚度激励及振动;进一步地,在工作载荷下所获得到的承载传动误差各阶频谱的幅值均有所减小,因此可有效降低高阶谐波引起的高阶次噪声问题。

(3)复合传动误差是由正弦函数和两段抛物线组成的,对应的加工过程中的瞬时滚比是由3部分基本滚比和高阶变性系数来实现,这在现有数控螺旋锥齿轮磨齿机上是比较容易实现的,验证了复合传动误差设计的加工可行性。