超临界二氧化碳向心透平设计与热流固耦合研究

赵攀,温玉聪,娄聚伟,杨培军,周林,张瑜,王江峰

(1.西安交通大学能源与动力工程学院,710049,西安;2.西安西热锅炉环保工程有限公司,710054,西安;3.国能长源汉川发电有限公司,432000,湖北孝感)

当二氧化碳的温度与压力分别高于其临界点(30.98 ℃,7.38 MPa)时,处于超临界态,形成超临界二氧化碳(SCO2)流体。在物理性质方面,SCO2密度高而黏度与可压缩系数低,其载热能力接近于液体,而流动性近似于气体;在化学性质方面,SCO2无色无味无毒,化学性质稳定,不易燃易爆[1]。已有诸多研究表明,以SCO2为工质的布雷顿循环发电系统具有结构紧凑、循环效率高、可在高温场合安全运行等诸多优势,预计在第四代核能反应堆、高温余热回收和火力发电等领域具有广阔的应用前景[2-4]。

近年来,国内外学者对SCO2布雷顿循环开展了一系列相关研究工作,其中部分国外研究机构起步较早,在十余年前就已开展了SCO2布雷顿循环系统的实验台搭建与试运行,例如日本东京工业大学(TIT)搭建的10 kW级SCO2布雷顿循环系统[5]、美国Sandia实验室(SNL)的250 kW再压缩闭式SCO2循环实验系统[6]、美国西南研究院(SWRI)的1 MW级SCO2布雷顿循环系统[7]以及韩国能源研究院(KIER)搭建的100 kW级SCO2循环系统[8]等。我国的研究机构也在近年陆续开展了若干SCO2循环实验系统的建设,并有一定的成果报道,例如中国科学院工程热物理研究所于近日建成的兆瓦级SCO2发电机组[9],上海电气集团有限公司的300 kW功率等级SCO2透平-压缩机同轴涡轮机组样机[10],西安热工研究院的5 MW级分流再压缩式SCO2发电实验平台[11]等。

在SCO2布雷顿循环系统中,SCO2透平将工质的内能转化为机械能并带动发电机做功,是系统的关键动力部件。在对SCO2透平的研究中,国内外学者采用的方法主要包括基于透平一维设计与性能预测的理论研究方法以及基于计算流体动力学(CFD)的数值模拟方法,这些研究所关注的透平形式则以单级向心透平为主。

在国外,Lee等[12]对应用于水冷小型模块化反应堆的SCO2布雷顿循环系统提出了叶轮机械一维设计方法,给出了透平与压缩机的变工况性能,并指出:在设计程序中用于计算透平内部流动损失的损失模型是基于空气透平以及蒸汽透平的相关研究成果的,可能不适用于SCO2工质的叶轮机械。Uusitalo等[13]用数值模拟方法研究了兆瓦级SCO2向心透平的流动损失,比较了不同设计速比下损失模型方法与数值模拟方法对透平内各区域流动损失的预测结果,结果表明:当透平的速比在0.50～0.65之间时,两者的预测结果相差不大,但是若设计速比较低,则两者会有较大的偏差。Holaind等[14]对小功率等级SCO2布雷顿循环系统进行了热力学建模分析,对其中的透平与压缩机开展了设计与数值模拟,在数值计算中采用了真实气体物性数据,结果表明透平的设计效率达到76%。Cho等[15]对应用于钠快冷堆的SCO2透平开展了一维与三维设计,获得了叶片型线的几何结构以及性能曲线。Kim等[16]用数值方法对某实验系统中采用的SCO2向心透平开展了气动分析,根据流动损失情况给出了叶片的改良设计方案。

在国内,Luo等[17]设计并用数值模拟方法研究了一台转速为6 000 r/min的单级离心式SCO2透平,并研究了其变工况性能,指出提高透平转速有助于达到高的透平效率。Ma等[18]在对SCO2向心透平开展数值模拟时考虑了流经动静叶间隙与轮背空腔的泄漏流体,并分析了轮背空腔的压力分布,定量计算了泄漏流对叶轮结构造成的轴向推力。周奥铮等[19]设计了转速为45 000 r/min的SCO2向心透平,用一维方法以及三维数值模拟方法分别获得了透平的变工况特性曲线,同时还基于一维向心透平效率预测对超临界二氧化碳循环进行热力学分析[20]。Lin等[21]采用热流固耦合方法,对一动叶入口直径约为40 mm的小型SCO2向心透平叶轮进行了单流道的流场数值模拟与强度校核,结果表明最大形变仅为0.1 mm,叶轮内部应力符合要求。Zhang等[22]分别设计了1.5 MW的SCO2向心透平以及15 MW的SCO2轴流式透平,分别对轴流式透平的叶片与向心透平的叶轮结构开展了强度校核。向心透平叶轮的强度校核中考虑了离心载荷与气动载荷的作用,但是未考虑温度的影响。吕国川等[23]开发了SCO2向心透平的一维设计程序,研究了透平的一维变工况性能预测方法,并用数值模拟方法证明了一维方法的可靠性。李翔宇等[24]基于遗传算法理念开发了向心透平热力优化设计程序与变工况性能预测程序,设计了5 MW级SCO2向心透平,并与CFD方法设计结果进行了对比。

目前国内外各实验系统的透平功率以及循环输出功率大多为百千瓦级,可预见更高功率等级的SCO2透平将在未来受到广泛关注。SCO2向心透平转速高、尺寸小、叶片薄,并在运行中受到高温高压高密度SCO2工质的冲击与传热作用,使透平叶轮发生受力应变与热膨胀。此外,向心透平的流量与叶轮尺寸随着功率等级的提高而增大,相对于小功率等级的透平,大功率等级透平的形变效应更加明显。因此在设计较高功率等级的SCO2向心透平时,有必要衡量叶轮在实际运行时的形变幅度与强度性能,以综合设计系统中转子与静子的尺寸,避免发生动静部件干涉等安全事故。目前国内外对SCO2向心透平开展的研究主要为气动特性分析,运行安全性分析偏少,且当前已有的安全性研究往往未能综合考虑透平在实际运行时的全部载荷,影响了计算结果的可靠性。

本文在1 MW功率等级SCO2向心透平设计的基础上,用求解雷诺平均Navier-Stokes方程(RANS)的方法开展三维数值模拟,分析了动叶轮的叶顶间隙对流动效率的影响,获得了透平的变工况性能曲线。使用热流固耦合方法,综合考虑透平实际运行中的旋转离心力、流体压力、温度以及轮背泄漏流等对轴向推力的影响,确定了设计工况下透平叶轮的形变与应力分布,研究结果可为兆瓦级SCO2布雷顿循环系统的综合设计提供参考。

1 SCO2向心透平一维设计

某SCO2布雷顿循环系统的主要组成部件包括热源、冷却器、回热器、透平与压气机,图1为该系统的流程图。表1所示为系统中向心透平的设计参数,图2为透平内部工质热力参数变化的焓-熵图。

向心透平的总-静等熵效率ηturb定义为工质在透平内的实际焓降与等熵焓降之比

(1)

式中:h2s为静叶栅入口CO2的总焓;h5s为动叶轮出口处CO2的等熵静焓;h5为动叶轮出口处的实际静焓。在透平的设计计算中,CO2工质的物性数据均采用物性数据库REFPROP中的真实气体物性。

表1 SCO2向心透平设计参数

在向心透平的一维设计理论中,透平的结构设计方案由表2所示的7个关键设计参数决定。

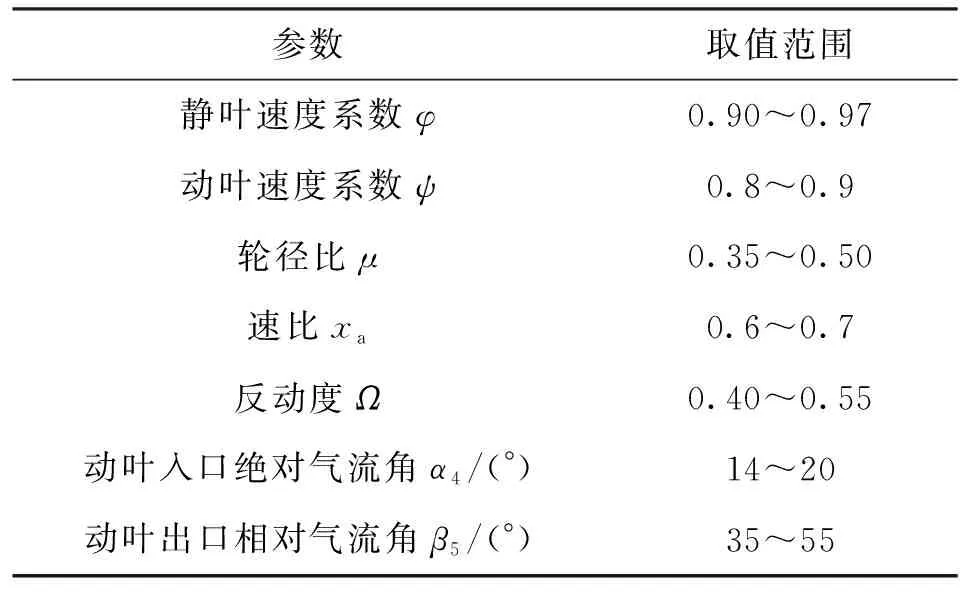
表2 7个关键设计参数的取值范围

在透平的一维设计计算中,首先在表2中选取一组数据作为初始值,然后通过向心透平一维设计理论确定透平的各关键几何参数,并用下式得到透平效率的预测值为

ηturb=2xa(μψcosβ5·

(2)

之后从透平的几何结构出发,用损失模型[23]估算透平运行时的各项流动损失,从流动损失方面获得透平效率ηturb,model,如果ηturb与ηturb,model之差小于准许误差ε,则认为透平的设计方案合理。图3所示为透平的总体设计流程,其中准许误差取0.5%。

向心透平一维设计程序可在表3所列的各参数取值范围中开展透平的一维设计并进行设计方案的筛选,通过不断迭代搜索,最终确定向心透平设计工况处的所有效率收敛且结构合理的透平设计方案。采用这些方案中效率最高的方案开展后续研究,表3给出了SCO2向心透平的一维设计结果。

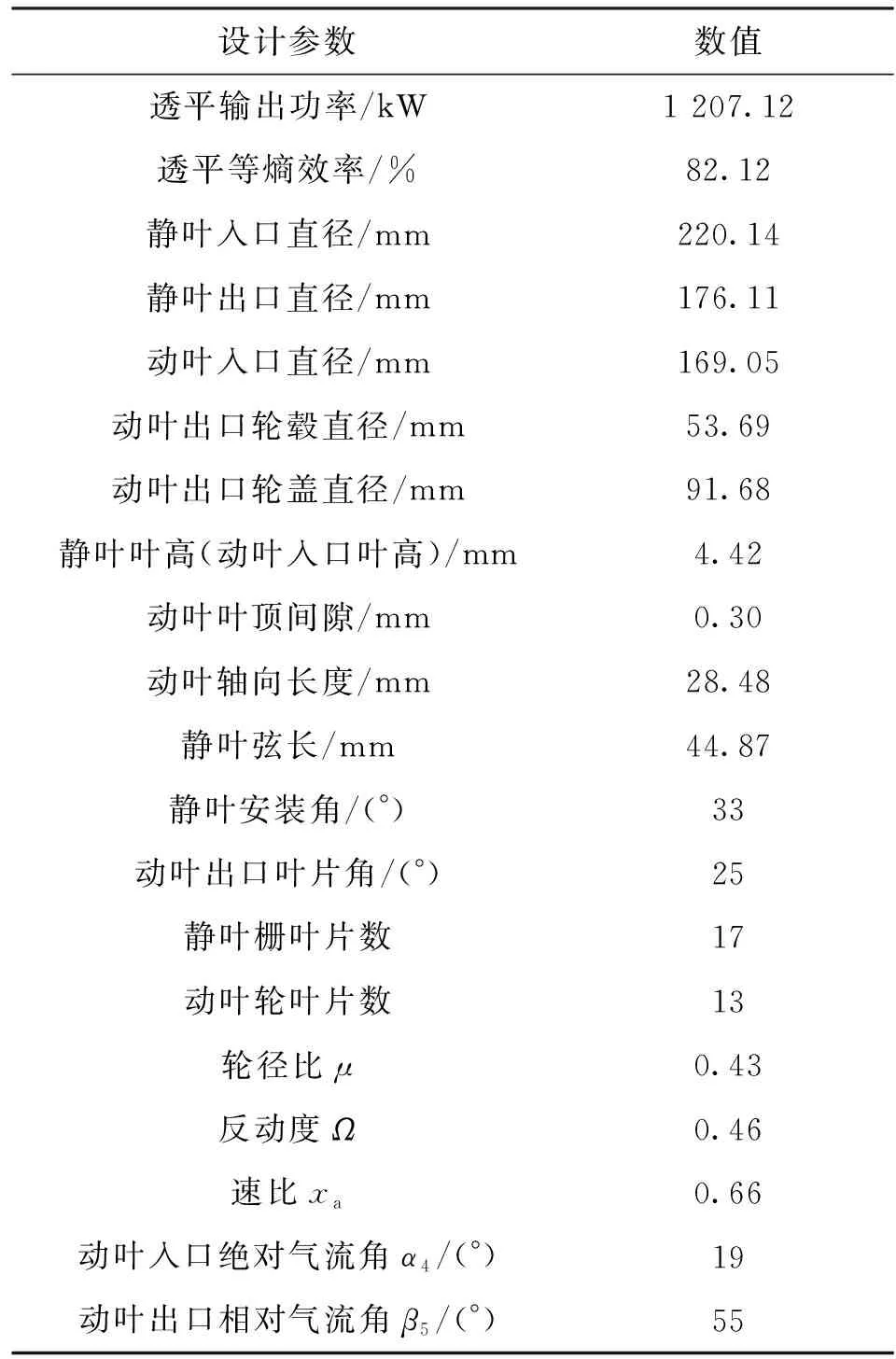
表3 SCO2向心透平一维设计结果

2 透平三维结构与数值模拟方法

2.1 透平三维几何结构确定与网格划分

根据向心透平一维设计方案的各项参数,使用ANSYS Bladegen建立透平动叶轮与静叶栅的三维几何模型,其中静叶栅采用TC-2P叶型,之后在ANSYS Turbogrid中进行动叶轮与静叶栅流道的流体域网格划分,其中动叶轮的网格包括了设计值为0.3 mm的叶顶间隙。图4与图5分别给出了本文设计的向心透平动叶轮与静叶栅的流道结构以及网格划分结果。

在ANSYS CFX中开展单流道、定常的三维数值模拟,为准确表示超临界态下CO2的物性,将物性数据库REFPROP中的CO2物性参数编制为高精度表格并由CFX调用。数值模拟基于求解雷诺平均Navier-Stokes(RANS)方程与k-ε湍流模型,边界条件为给定动叶轮出口静压7 820 kPa、静叶栅入口温度773.15 K以及质量流量18 kg/s;动静交界面设置为冻结转子模型,此模型适用于动、静叶网格能够较好贴合的情况,具有鲁棒性好且计算资源消耗少的优点;数值计算的收敛残差设置为10-5。

2.2 网格无关性验证

为了分析网格数对计算结果的影响,静叶栅和动叶轮单流道的计算网格数均分别选取为20万～90万,并在相同的边界条件下开展数值模拟。

表4给出了网格无关性验证结果,可见当网格数大于50万后,仿真结果偏差较小。综合考虑计算机算力以及计算精度的需求,后续研究中动叶轮与静叶栅的网格数均选取50万。

表4 网格无关性验证结果

表5给出了SCO2向心透平关键参数的一维设计值与数值模拟值的对比结果,可见各参数的相对偏差较小,最大偏差为2.35%,说明透平的一维设计方法可行。

表5 SCO2向心透平关键参数设计值与模拟计算结果的对比

3 数值模拟结果分析

3.1 透平内部流动分析

图6分别给出了设计工况下SCO2向心透平轮毂面与叶片表面的压力分布、流道内的流线分布以及各叶高截面的熵分布。

由图6(a)可知,透平内部压力随流动方向连续降低,静叶栅入口处的平均压力为13.62 MPa,透平的膨胀比为1.74,与设计值基本一致。在静叶栅中,流道的压力分布与叶高无关,轮毂面上的等压线基本与工质的流动方向垂直,静叶栅喉部处的压力梯度最大,动-静叶交界面处的流体压力分布较为均匀,平均压力为10.82 MPa;在动叶轮中,工质的压降主要发生在流道的前半段,叶片压力面受到气流冲击作用,其压力高于吸力面。

由图6(b)可知,工质在静叶栅中基本贴合叶片壁面流动,在静叶栅流道内,工质流速先增大后减小,在叶栅喉部达到最大值,最大流速为346.9 m/s,对应马赫数为0.842。动叶入口气流角接近于90°,基本实现了轴向进气。动叶入口处有部分流体冲击叶片压力面前缘,并在叶片的压力面附近形成了小范围的回流涡与流动分离;在动叶轮的叶顶部位,部分流体并未推动叶片做功,而是通过叶顶间隙从压力面侧泄漏进入吸力面侧,那之后流体速度明显降低并形成了涡旋,干扰了主流流动。

透平流道内的熵增区域一般对应着流动损失较大的区域,由图6(c)可知,动叶流道内,各叶高的熵增区域均始于叶片前缘,其中吸力面附近存在明显的熵增区域,其面积随叶高的增大而增大,说明能量损失随叶高增大,推测此处的熵增现象是由叶顶间隙泄漏流引起的;而压力面附近的熵增现象则弱于吸力面,且随着叶高的增大而减弱,推测此处的熵增是由叶片前缘压力面的回流涡引起的,可见其造成的流动损失相对较小。

3.2 叶顶间隙对透平效率的影响

叶顶间隙泄漏流动影响了透平的通流性能,需要尽量减小叶顶间隙的取值,但是过小的叶顶间隙会使动叶轮的叶片容易与静止的轮盖面发生碰撞,影响运行安全性。本文研究了泄漏流的流动特征,确定了叶顶间隙大小与透平效率的关系。

图7所示为0.3 mm叶顶间隙(6.78%动叶入口叶高)与1.1 mm叶顶间隙(25%动叶入口叶高)下叶顶间隙泄漏流体的流线分布。可见工质在经过叶顶间隙后发生了流动分离,流动速度明显降低并在叶片吸力面附近形成涡旋流动。在0.3 mm的叶顶间隙下,泄漏流的影响范围约占流道体积的1/4,涡旋局限于叶片吸力面与轮盖面附近,其沿流动方向先以较慢的速度扩张,然后逐渐消散,叶片中后部的涡旋现象已不明显;在1.1 mm的叶顶间隙下,泄漏流的影响范围约占据了流道体积的1/2,叶片吸力面附近的涡旋随流动方向扩张很快,涡旋甚至可达下一叶片的压力面附近,对主流形成了强烈的扰动作用。

图8给出了不同叶顶间隙大小的SCO2向心透平在额定工况运行时的总-静等熵效率,可见效率随叶顶间隙的增大以越来越快的速率减小。在叶顶间隙从6.78%入口叶高逐步增大至40%入口叶高的过程中,透平效率从83.53%降低至72.63%。当叶顶间隙较小时,透平效率仍可保持在80%以上,且此时叶顶间隙的增大对透平效率的影响较小,当叶顶间隙达到20%入口叶高后,透平效率的降低幅度明显加快。因此,对于所设计的兆瓦级SCO2透平,为保证较好的通流效率,叶顶间隙不宜超过动叶入口叶高的20%。

3.3 透平的变工况性能

透平的变工况数值模拟的边界条件为给定入口总压、入口温度与出口静压,同一转速选取多个入口总压进行仿真分析,得到了兆瓦级SCO2向心透平在设计工况与变工况下的运行性能。

图9为25 000 r/min、30 000 r/min以及35 000 r/min 3种不同转速下的透平膨胀比-效率曲线。可见3个转速下均存在使透平总-静效率达到最高的最佳膨胀比,当转速为设计转速30 000 r/min时,透平的总-静效率在设计工况的膨胀比1.74附近具有最大值83.53%;当转速偏离30 000 r/min时,透平效率的最大值点有所偏移,在25 000 r/min与35 000 r/min的转速下,透平的最佳膨胀比分别为1.56与1.96,对应的最大总-静效率分别为79.24%与85.72%。总体而言,本文设计的兆瓦级SCO2向心透平可在膨胀比1.7～4.0、转速25 000 r/min～35 000 r/min的范围内保持较高的效率,说明其变工况性能良好。

4 透平叶轮热流固耦合安全性分析

4.1 热流固耦合结构强度计算设置

由SCO2透平的数值模拟结果可见,透平动叶轮轮毂面与叶片在运行时将受到7 MPa～14 MPa的流体压力作用,同时流道内工质温度的取值范围约为400 ℃～500 ℃,因此叶轮结构在运行时会发生受力变形与热膨胀。为了准确评估叶轮的形变特征,保障透平的安全运行,本文综合考虑了透平实际运行中受到的各项载荷,使用热流固耦合方法计算了所设计的兆瓦级SCO2透平在设计工况稳定运行时的强度性能。

4.1.1 透平全周流动性能数值模拟

使用CFX的Transform Mesh功能,由已有的单流道网格得到透平动叶轮与静叶栅的全周计算网格。在透平的设计工况下开展了全周数值模拟,获得了透平全周流道内的温度与压力分布,为后续的透平叶轮运行安全性分析提供基础数据。表6分别给出了全周计算与单流道计算得到的透平功率、入口总压以及总-静效率,可见两者差异很小。

表6 透平全周计算结果与单流道计算结果的对比

4.1.2 透平叶轮实体模型建立与网格划分

叶轮流道部分的几何结构由前文数值模拟研究给出的轮毂面形线与叶片曲面确定,其余部分的设计则参考了Sandia实验室的再压缩SCO2布雷顿循环系统[6]所用的透平叶轮形式,叶轮采用轴孔-轴的方式与主轴配合,轮背中心轴孔处设计了圆台以方便密封结构的加工并保证足够的轮-轴配合尺寸。透平叶轮的几何模型如图10(a)所示,其剖面图与关键几何尺寸如图10(b)所示。

透平叶轮材料选择为牌号TC4的钛合金(Ti-6Al-4V),该材料可在SCO2向心透平的运行工况下保持良好的高温力学性能,在400 ℃～600 ℃的温度范围内,其屈服强度σ0.2在376.7 MPa～504.9 MPa之间[25]。

在ANSYS Mechanical中开展叶轮的固体域网格划分,其中对叶轮轮毂面与叶片表面的网格进行了加密以确保热流固耦合数据传递的准确性。以气动载荷与温度载荷分别引起的最大形变为基准进行了网格无关性验证,结果见表7,可见网格数达到58万之后,两最大形变的计算结果变化均不大,因此最终采用了58万的固体域网格数。图11所示为透平叶轮的网格划分结果。

表7 透平叶轮固体域网格无关性验证

4.1.3 热流固耦合计算中各载荷的处理

在透平长期保持额定工况运行时,认为其传热达到稳定,此时SCO2流体与叶轮实体无热交换,叶轮的固体壁面和流体底层保持温度相等。在ANSYS Mechanical的Steady-State Thermal模块中,以透平全周流动数值模拟所获得的流体温度在流固交界面上的分布为初始条件,计算获得叶轮结构内部及其余表面的温度场。图12所示为透平叶轮的温度分布,可见叶轮的最低温度与最高温度分别为418.4 ℃与483.2 ℃,总体温度分布具有旋转对称的特征。

在透平的实际运行中,部分高温高压的SCO2流体会经由动静叶间隙泄漏进入轮背与静子之间的空腔,轮背空腔内的泄漏流压力作用于轮背面上,形成轴向推力。为考虑其影响,本文基于Ma等[18]关于轮背泄漏流压力分布的数值模拟结果推导出轮背面相对位置与压力的关系,据此在轮背面上加载了从轮缘处10.82 MPa线性降低至圆台边缘9.33 MPa的压力载荷。

透平叶轮的热流固耦合计算综合考虑了透平叶轮结构的温度场、叶片与轮毂面上的气动力、高转速引起的离心力以及轮背泄漏流对轮背面的压力,其计算设置见表8。

表8 SCO2向心透平叶轮热流固耦合计算设置

4.2 透平运行安全性分析

图13分别给出了气动载荷以及温度载荷引起的透平叶轮形变,其中轴向形变以叶轮的排气方向为正方向,且离心载荷默认加载。

由图13可知,动叶轮的叶片受到工质的冲击作用,叶片尾缘的叶顶部分出现了正向最大0.223 mm的轴向形变;叶轮轮毂面受到高压工质的压力作用,使得轮缘处出现了负向最大0.823 mm的轴向形变,叶轮总形变的最大值为0.830 mm,位于轮缘部位。在温度载荷的影响下,叶轮产生了较为均匀的膨胀,距离叶轮旋转轴最远的轮缘部分膨胀的最为剧烈,出现了0.514 mm的最大总形变,叶轮的轴向形变为-0.199 mm～0.208 mm。

图14给出了泄漏流压力载荷的作用下叶轮发生的轴向形变。由于叶轮轮缘部分结构最薄且受力最大,该处出现了1.012 mm的轴向形变,叶轮的轴向形变分布类似于上述透平气动载荷作用下的分布,但是方向相反。

图15给出了综合考虑温度载荷、离心载荷、气动载荷以及泄漏流引起的压力载荷时SCO2向心透平的轴向形变、径向形变与总形变,可见透平叶轮的轴向形变在-0.199 mm～0.304 mm之间,其中叶轮排气方向(正向)的最大轴向形变为0.304 mm;在温度的影响下,叶轮在径向上表现出整体膨胀的趋势,叶轮结构的最大总形变出现在叶轮轮缘处,为0.570 mm。

图16给出了考虑所有载荷时透平叶轮的von Mises等效应力分布图。可见透平叶片以及轮毂面上的应力均不超过188.5 MPa,动叶片上的最大应力出现于叶片中前部与轮毂面的连接处,大小约为160 MPa;叶轮结构上的最大应力为282.4 MPa,出现在圆台面与轮背面交界处的应力集中区域,此最大值远小于TC4材料在透平的工作温度范围下的屈服强度[25],说明透平叶轮结构强度合格,在额定工况运行时不会出现明显的塑性形变。

5 结 论

本文在MW级SCO2向心透平设计的基础上,使用三维数值模拟方法研究了透平的工质流动特征与变工况性能,使用热流固耦合方法对透平动叶轮在额定工况下的运行安全性进行了校核,得出了以下结论:

(1)在指定的初始设计参数下完成了兆瓦级SCO2透平的设计,透平的设计功率为1 207.12 kW,效率为82.12%;在设计工况下透平功率的数值模拟值为1 188.57 kW,透平气动效率达到83.53%,透平功率与设计值偏差为1.54%,验证了设计方法的可靠性。

(2)当叶顶间隙增大时,透平效率以越来越快的速率降低,为保证较好的通流性能,叶顶间隙应小于动叶入口叶高的20%;变工况特性研究表明,该透平在膨胀比1.7～4.0以及转速25 000 r/min～35 000 r/min的运行范围内具有良好的通流性能。

(3)设计工况下,采用TC4钛合金材料的透平叶轮沿排气方向的最大轴向形变为0.304 mm,在透平的实际运行中,叶顶间隙应避免动叶叶顶与轮盖面在运行时相互摩擦;叶轮结构的最大总形变为0.570 mm,最大应力值为284.2 MPa,最大应力远小于材料在相应温度下的屈服极限,表明其结构强度符合要求。

(4)透平在设计工况下运行时,温度载荷、气动载荷以及轮背泄漏流引起的轴向推力在透平轮缘处分别引起了0.830 mm、0.514 mm、1.012 mm的形变,三者的影响均不可忽略。因此,热流固耦合方法可以有效实现SCO2向心透平的运行安全性研究,在指导相关科学研究与工程应用方面具有一定的参考价值。