迷宫蜂窝密封泄漏特性的实验测量和数值研究

向新,晏鑫,李志刚,李军

(西安交通大学叶轮机械研究所,710049,西安)

旋转动密封是现代透平机械中的关键部位,先进的转子和静子间的旋转动密封技术可显著提高透平机械的工作效率和稳定性。随着透平机械向着高温度、高压力、高转速方向发展,密封不仅需要控制泄漏流动,还需改善其转子动力特性[1]。相比于迷宫密封,蜂窝密封具有优良的转子动力特性,因此被广泛应用于航空发动机、燃气轮机、汽轮机和其他透平机械的轴封和叶顶间隙密封[2-4]。

迷宫蜂窝密封是一种常见的蜂窝密封结构,根据迷宫齿结构不同可分为直通式迷宫蜂窝密封、台阶式迷宫蜂窝密封和高低齿迷宫蜂窝密封。针对直通式迷宫蜂窝密封的研究较多,早在1978年,Stocker等[5]就实验研究了直通式迷宫蜂窝密封的泄漏特性,研究表明密封间隙和蜂窝孔径是决定密封泄漏量的关键几何参数。其后,Childs等[6]也通过实验发现蜂窝孔径和深度能够显著影响直通式迷宫蜂窝密封的泄漏量。Nayak等[7-8]数值研究了转速、蜂窝面磨损对直通式迷宫蜂窝密封泄漏特性和风阻加热的影响,研究表明:存在一个临界转速,该临界转速与泰勒数与雷诺数的比值有关;蜂窝面磨损使有效密封间隙增大导致泄漏量增加,但流体总温升降低。聂顺鹏等[9]实验研究发现直通式迷宫蜂窝密封的泄漏量与流量系数比光滑面迷宫密封分别降低了约20%、10%。Wodzimierz等[10-11]通过数值和实验研究表明迷宫齿倾斜角、齿高、齿厚和齿位置对直通式迷宫蜂窝密封泄漏量影响很大,文中对迷宫齿几何参数进行了优化使密封流量系数降低了17%。Chougule等[12]提出了一种中心交错的蜂窝改进结构应用到直通式迷宫蜂窝密封中,并对其密封特性进行了数值研究。研究表明,采用交错蜂窝密封结构使流量系数相比常规蜂窝密封降低9%。

Schramm等[13]实验研究台阶式迷宫蜂窝密封的泄漏特性,文中提出有效密封间隙的概念,指出蜂窝孔径使有效密封间隙增大而导致泄漏量增加。Kool[14]、Paolillo[15]等采用实验和数值方法研究了转速对台阶式迷宫蜂窝密封泄漏特性的影响,研究表明:在较小速比条件下,泄漏量受转速的影响较小,但当速比大于5,泄漏量减少约20%。Mohammad等[16]数值研究迷宫齿不同几何参数对光滑面和蜂窝面台阶式迷宫密封泄漏特性影响。研究表明在小间隙中,随着迷宫齿宽度的减小,光滑面迷宫密封的流量减小,而迷宫蜂窝密封的流量增加。Yan等[17-19]建立了台阶式迷宫蜂窝密封的计算模型,数值研究了压比、密封间隙、转速、蜂窝孔径对其泄漏特性和总温升特性的影响。陈秀秀等[20]数值研究了动叶叶顶蜂窝密封的泄漏特性,研究表明密封间隙越大,密封内泄漏量近似线性增加;存在最佳的蜂窝孔径使泄漏量最少。

Li等[21]数值研究了密封间隙、转速、蜂窝孔径和深度对高低齿迷宫蜂窝密封泄漏特性的影响,研究表明:密封泄漏量与间隙成正比,当转速高于3 000 r/min时密封泄漏量开始显著降低;当蜂窝孔径和迷宫齿宽数值相同,蜂窝深径比为0.93时,密封泄漏量最低。李志刚等[22-24]将高低齿迷宫密封的低齿替换为蜂窝结构,数值研究了蜂窝孔径和深度对蜂窝密封特性的影响。孙丹等[25]通过实验测量与数值计算对光滑面蜂窝密封的泄漏特性进行了研究,研究指出:蜂窝结构参数主要是通过影响蜂窝孔中涡系的发展和蜂窝孔的密度来影响泄漏量的。

目前对于蜂窝密封的研究主要集中在直通式迷宫蜂窝密封和光滑面迷宫密封上,对于具有高低齿迷宫蜂窝密封的研究较少。本文通过实验测量和数值模拟对高低齿迷宫蜂窝密封的泄漏特性进行研究。在密封泄漏特性静止实验台测量了7种压比和5种密封间隙下高低齿迷宫蜂窝密封的泄漏量。接着,基于实验数据对数值方法准确性验证的基础上,数值研究压比、密封间隙、转速和蜂窝孔径对迷宫蜂窝密封泄漏特性的影响,并与光滑面迷宫密封的泄漏特性进行了比较。

1 实验系统和模型

图1是密封泄漏特性静止实验系统示意图。实验系统由压缩机气源、管路、整流系统、试验段、试验件和测量和控制系统等组成。实验介质为压缩空气,压缩空气最多由4台螺杆压缩机提供,气流的最高进口压力为0.7 MPa,最大流量为2 kg/s。在整流段前端设有压力调节阀门和旁路,以调节和控制进入试验段气流的流量和压力。DN80罗托克气体涡轮流量计(精度±1%)安装在整流段前,用于测量空气的流量。三孔探针和K型热电偶位于试验段前部,以测量泄漏流的压力和温度。其中测量的压力和温度的误差分别约为±0.2%和±1 K。

图2是密封泄漏特性静止实验台图片。在实验过程中,首先根据实验需要,由压气机提供一定的压力的气流,压缩空气通过管路进入到整流段中;其次,在整流段中对流量进行微调,使试验段进口处压力满足实验要求;等进口压力稳定后,读取三孔探针测量的压力读数,同时记录流量计流量和K型热电偶测量的温度读数。

图3给出了迷宫蜂窝密封和光滑面迷宫密封几何结构图,其主要几何参数已在图中标注,迷宫蜂窝密封的静子面为蜂窝结构。

图4是迷宫蜂窝密封实验件实物图,由蜂窝静子面和迷宫转子面两部分组成。实验件为平板结构,长95 mm,宽320 mm。实验为静态平板实验,不考虑篦齿盘弧度及转速的影响,主要测量迷宫蜂窝密封在不同压比(1.05～1.6)和径向间隙(0.4～1.2 mm)下的泄漏量,以研究压比和间隙对其泄漏特性的影响以及验证数值方法的正确性。实验中实验件的蜂窝孔径和厚度分别保持为1.6 mm和0.1 mm。

在实验基础上验证数值方法的正确性后,为接近密封真实工况,建立了考虑篦齿盘弧度的密封模型,其旋转半径r为437.5 mm。数值研究压比、径向间隙、转速和蜂窝孔径对迷宫蜂窝密封泄漏特性的影响。同时为评估迷宫蜂窝密封的性能,建立了对应的迷宫密封模型,其几何参数如图3(b)所示。

2 数值方法

图5给出了迷宫蜂窝密封的三维计算域模型。为节约计算资源,考虑到密封结构的周期性,取两个蜂窝孔径的弧段作为研究对象的计算域,弧段两侧采用周期性边界。采用商用软件ICEM生成多块结构化网格,对壁面附近的网格进行加密,以满足y+的要求。在密封间隙处网格节点数保持在20个以上。图6是迷宫蜂窝密封网格示意图。

表1给出了迷宫蜂窝密封的计算边界条件,进口总温和出口静压分别保持为285 K和98.3 kPa,压比和计算转速范围分别为1.05～1.6和0～8 000 r/min。

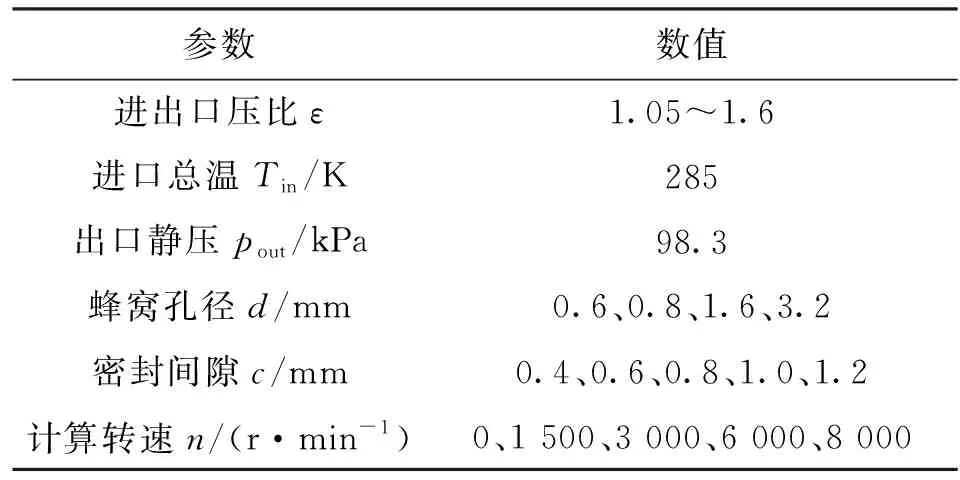
表1 迷宫蜂窝密封几何参数和计算工况

此外还计算了5种径向间隙和4种蜂窝孔径的泄漏量以研究密封间隙和蜂窝孔径对迷宫蜂窝密封泄漏特性的影响。迷宫密封的计算边界条件同迷宫蜂窝密封保持一致。

表2给出了本文数值计算采用的求解方法,本文基于标准k-ε两方程湍流模型和三维Reynolds-averaged Navier-Stokes(RANS)方程求解方法,采用商用CFD软件ANSYS CFX数值分析了压比、密封间隙、转速和孔径对蜂窝密封泄漏特性的影响,并与对应的迷宫密封泄漏特性进行了比较。计算使用的工质为理想气体;近壁面区采用改进壁面函数法;固壁面视为绝热、光滑壁面;采用高精度离散模型。

表2 密封泄漏特性数值方法

当动量方程的残差数量级达到10-6、连续方程的残差数量级小于10-6、进出口流量差小于0.1%时,可认为计算收敛。

2.1 网格无关性验证

在压比为1.3,密封间隙为1.0 mm工况条件下,选取3套网格数目分别为117万、137万和173万的网格,以迷宫蜂窝密封的泄漏量为考核指标,进行网格无关性验证。计算结果如表3所示,当网格数从137万增加到173万时,密封泄漏量偏差小于0.5%,可以视为网格无关。在后续不同计算模型中,网格数均大于137万,确保满足网格无关性精度要求。

表3 迷宫蜂窝密封泄漏量网格无关性验证

2.2 数值方法有效性验证

采用径向间隙为1.0 mm的迷宫蜂窝密封,以不同压比下密封泄漏量为考核指标,对本文采用的湍流模型进行了验证,结果如图7所示。3种湍流模型随压比的增长趋势同试验数据一致,泄漏量都随着压比的增大而接近线性增加,其中标准k-ε湍流模型具有更好的预测精度,计算与试验结果偏差在5%以内,满足计算精度要求,因此证实本文采用的湍流模型能够准确预测迷宫蜂窝密封泄漏量。

图8是迷宫蜂窝密封泄漏量实验数据与计算结果对比图。在不同的径向间隙下密封泄漏量均随着压比的增加而接近与线性增长;密封泄漏量与径向间隙大小成正比。同时,实验测得的泄漏量要略大于数值计算的结果,但相对误差小于7%。误差是客观存在的,造成该误差的主要原因有:第一,蜂窝板经过线切割成形后,采用焊接的方式与蜂窝底板固连,加工过程对蜂窝形状、尺寸等造成一定影响,从而不可避免地使实验件尺寸与计算模型尺寸产生一定偏差;第二,线切割加工的密封齿表面较为粗糙,可能对实验结果产生一定影响。总体上可认为数值预测结果和实验测量数据吻合良好,验证了数值方法的准确性。

3 结果分析与讨论

在验证完数值方法的准确性和可靠性的基础上,建立考虑篦齿盘弧度的密封模型,数值研究了压比、密封间隙、转速和蜂窝孔径对迷宫蜂窝密封泄漏特性的影响,揭示其封严机理。同时与迷宫密封进行了比较。在密封计算中,理想流量mid定义为

(1)

A=2πrc

(2)

式中:Tin是进口总温;pin是进口总压;A是间隙通流面积;Rg为气体常数;κ为定熵指数。

本文采用无量纲流量系数φ[2]对密封泄漏特性开展研究

(3)

(4)

式中:mtotal是迷宫蜂窝密封整周泄漏量;mcell是最小周期弧段泄漏量;θ为最小周期单元的周向角。

3.1 压比和径向间隙的影响

研究了压比和径向间隙对迷宫蜂窝密封泄漏特性的影响,并同光滑面迷宫密封进行了对比,其中蜂窝孔径保持为1.6 mm。

图9是在转速为3 000 r/min时,两种不同径向间隙下迷宫蜂窝密封和光滑面迷宫密封的流量系数随压比的变化图。尽管光滑面迷宫密封和迷宫蜂窝密封的静子面结构不同,但两者的流量系数均随着压比的增大而增大,并且增加的趋势在减缓。如迷宫蜂窝密封间隙为1.2 mm时,压比从1.05增加到1.3时,流量系数增加约130%,压比从1.3增加到1.6时,对应的流量系数仅增加约24%。流量系数随压比的增加而增长趋势减缓的原因主要是压比较小时,流体还未充分节流膨胀,导致泄漏量显著增加;压比较大时,流体在迷宫齿和蜂窝腔室中形成了强烈的旋涡,流体能量得到充分耗散,泄漏量增加趋势变缓。

由图9可知径向间隙为0.4 mm时,迷宫蜂窝密封的流量系数要小于光滑面迷宫密封;在径向间隙增长为1.2 mm时,光滑面迷宫密封的流量系数要小于迷宫蜂窝密封。该现象说明,在小径向间隙下迷宫蜂窝密封比光滑面迷宫密封拥有更优的密封性能,在大径向间隙时则相反。

图10是在转速为0 r/min和3 000 r/min时,迷宫蜂窝密封的流量系数随径向间隙的变化图。在不同的转速下随着间隙的增加,流量系数略有减低。流量系数从径向间隙0.4 mm增加到1.2 mm最大降低约10%。实验表明,迷宫蜂窝密封的泄漏量随着径向间隙的增大而增加,这主要是因为径向间隙的增加使通流面积增加,导致泄漏量增加。造成流量系数随着间隙的增加而略有减低的主要原因,是高低齿迷宫和台阶结构对于流体的阻挡作用明显,虽然径向间隙增加导致通流面积增加使泄漏量增大,但是相对理想泄漏量增大的幅度较小,所以流量系数反而略有减低。这与蜂窝面直通式和台阶式迷宫密封有明显的不同。

图11是在压比为1.3、径向间隙c分别为0.4 mm和1.2 mm时光滑面迷宫密封和迷宫蜂窝密封的局部速度矢量分布图。从图11中发现:在径向间隙为0.4 mm时,光滑面迷宫密封和迷宫蜂窝密封的流场不同;蜂窝面使高齿齿顶间隙处的射流角度发生了偏转,带动高齿齿后所有的流体顺时针运动形成了一个完整的旋涡,流体耗散效应明显。对于光滑面迷宫密封而言,齿顶的射流仅带动高齿齿后的上半部分的流体形成一个耗散较强旋涡,而下半部分流体形成的旋涡能量耗散很弱。此外,在径向间隙小时,流体速度也较低,流入蜂窝孔中进行耗散的流体也就更多。以上原因使得在小径向间隙下,迷宫蜂窝密封比光滑面迷宫密封拥有更优的密封性能。

从图11中还可看出,径向间隙为1.2 mm时的射流速度比径向间隙为0.4 mm时的射流速度大,这会使射流撞击高齿和台阶时造成更大的损失,使泄漏量降低。一方面,径向间隙增加使通流面积增加,泄漏量增大;另一方面,径向间隙增加使射流撞击迷宫齿和台阶的损失增大,泄漏量减少。这两方面的原因造成迷宫蜂窝密封的流量系数随径向间隙增加而略有减低。

3.2 转速的影响

本小节研究了转速对迷宫蜂窝密封泄漏特性的影响,转速范围为0～8 000 r/min,径向间隙为0.6 mm和1.2 mm,蜂窝孔径保持为1.6 mm。图12给出了在2种不同的径向间隙时迷宫蜂窝密封和光滑面迷宫密封流量系数随转速变化的变化图。

由图12可知,迷宫蜂窝密封转速范围在0～3 000 r/min时流量系数变化不大,当转速大于3 000 r/min时,流量系数开始快速降低。如迷宫蜂窝密封在密封间隙为0.6 mm,压比为1.3时,转速由0 r/min变化到3 000 r/min时,流量系数下降了约2.7%,转速由3 000 r/min变化到8 000 r/min时,流量系数下降了约22%。同时,压比越小,流量系数降低得幅度越大,在径向间隙为0.6 mm、压比为1.6时,迷宫蜂窝密封的流量系数降低了19%;当压比为1.05时流量系数则降低了51%。

由图12(a)可以看出,光滑面迷宫密封的流量系数虽然也随着转速的增大而降低,但是降低的幅度要低于迷宫蜂窝密封。在转速大于6 000 r/min时,3种不同压比下迷宫蜂窝密封的流量系数均低于光滑面迷宫密封。这表明转速对迷宫蜂窝密封泄漏特性的影响更大,在高转速工况下迷宫蜂窝密封拥有更好的密封性能。但是这种影响会随着径向间隙的增大而被减弱。如图12(b)所示,当径向间隙增大为1.2 mm时,流量系数随转速升高而降低的趋势减缓。这主要是因为在大径向间隙时流体的轴向速度较大,由轴旋转带动流体产生的周向速度对主流的影响较低,流体沿周向运动的趋势不强,蜂窝孔中流体的耗散作用弱。

图13给出了迷宫蜂窝密封在3种不同转速时密封子午面流线和湍动能云图。如图13(a)所示:在转速为0时,蜂窝孔中基本只形成一个旋涡,并且旋涡中心靠近蜂窝孔底部;湍动能数值较小且主要集中分布在密封齿顶间隙处。随着转速的升高,转子面带动近壁面流体沿旋转方向运动,在密封中产生周向流动,有更多的流体流入孔中使蜂窝孔中流体耗散加强。如图13(b)所示:在转速增长为3 000 r/min时,蜂窝孔中的旋涡个数增加,耗散加强;由于旋转使轴近壁面的流体沿旋转方向运动,高齿后部腔室中较小的旋涡变得更小。如图13(c)所示:当转速达到8 000 r/min时,蜂窝孔中的旋涡也变得更加复杂,流体耗散进一步加强,高齿后部腔室中较小的旋涡消失;同时,湍动能明显增大,流体挤压造成的损失增大使密封泄漏量降低。综上所述,随着转速的升高,流体周向运动速度增大,孔中流体的耗散加强使泄漏量降低,同时流体之间的相互挤压也更剧烈造成泄漏量降低。

在小压比和小径向间隙时,泄漏流体的轴向速度较小而周向速度大,这使密封中流体沿周向运动的趋势加强,孔中流体耗散加强,转速对密封泄漏特性影响更大。对于光滑面迷宫密封而言,没有类似迷宫蜂窝孔结构造成更多的损失,这使得转速对其泄漏特性的影响较小。

3.3 孔径的影响

蜂窝孔径是迷宫蜂窝密封件的重要几何参数之一。Schramm等[13]提出有效密封间隙ceff的概念以分析孔径对密封泄漏特性的影响。

图14是有效密封间隙ceff的示意图。值得注意的是,当蜂窝孔径d小于齿顶宽度b(本文为0.6 mm)时,有效密封间隙ceff等于密封间隙c。ceff的表达式如下

(5)

本小节研究了5种不同蜂窝孔径(0、0.6、0.8、1.6、3.2 mm)对迷宫蜂窝密封泄漏特性的影响,其中密封间隙保持为0.6 mm,转速为3 000 r/min。

图15给出了5种不同压比下迷宫蜂窝密封流量系数随蜂窝孔径变化关系图,其中将光滑面迷宫密封视为蜂窝孔径为0时的密封。随着孔径的增大,密封流量系数先降低后升高,在蜂窝孔径d为0.6 mm时密封流量系数最低。当蜂窝孔径从0增大到0.6 mm时,泄漏系数降低3.0%～5.5%;当孔径从0.6 mm增大到3.2 mm时,泄漏系数增大17%～20%。同时还可从图中15发现,孔径d为1.6 mm时的流量系数几乎与孔径d为0 mm时一样。这表明当孔径d小于1.6 mm时,迷宫蜂窝密封的流量系数低于光滑面迷宫密封。即当蜂窝孔径d小于1.6 mm时,迷宫蜂窝密封的封严性能优于迷宫密封。

图16给出了4种典型的蜂窝孔径0、0.6、1.6和3.2 mm子午切面上局部速度云图和流场分布图,此时密封压比为1.3,转速为3 000 r/min。如图16(a)所示:当孔径为0时,有效密封间隙ceff与径向间隙c一致,流经高齿齿顶间隙的射流沿轴向水平流动,带动齿后的流体形成了上下两个旋涡。如图16(b)所示:当孔径增长为0.6 mm与齿宽数值一致时,有效密封间隙ceff与径向间隙c差别不大,其流场分布与孔径为0时的流场分布较为一致。蜂窝孔径增大使更多流体进入蜂窝孔内部,使流体的能量在孔中耗散降低了密封泄漏量。这在数值上表现为孔径从0增长到0.6 mm时,流量系数呈现出下降的趋势。如图16(c)所示:当孔径增长为1.6 mm时,从图中和式4均可知道此时的有效密封间隙ceff开始增大,齿顶射流开始向下偏转,其流场已与孔径为0.6 mm时的流场不同;同时从速度云图中发现流体在蜂窝孔内的速度升高,蜂窝孔对气流的耗散作用加强。在孔径为1.6 mm时,一方面有效密封间隙增大使通流面积增加导致泄漏量增大,另一方面蜂窝孔对气流的耗散作用增强使泄漏量降低,这两种原因导致孔径为1.6 mm时的流量系数与孔径为0 mm时一致;孔径从0.6 mm增长到1.6 mm时,密封流量系数也就升高。如图16(d)所示,当孔径增长为3.2 mm时,有效密封间隙显著增大,流场发生了很大变化,此时蜂窝孔对气流的耗散作用加强,但是由有效密封间隙增大带来的泄漏量增加占主导作用,所以孔径从1.6 mm增长到3.2 mm时,流量系数升高。

综上,当孔径小于齿宽时,有效密封间隙为密封间隙,随着孔径的增大蜂窝孔对气流的耗散作用加强,流量系数下降;当孔径大于齿宽时,虽然随着孔径增大使蜂窝孔对气流的耗散进一步加强,但是有效密封间隙增大导致的泄漏量增加占比更大,流量系数升高。当孔径升高到1.6 mm时,流量系数已与光滑面迷宫密封一致,孔径高于1.6 mm的迷宫蜂窝密封的封严性能已经要低于光滑面迷宫密封了。

4 结 论

(1)迷宫蜂窝密封泄漏量随着压比的增加而线性增加;迷宫蜂窝密封和光滑面迷宫密封流量系数均随着压比的增加而增加,但是增加趋势在减缓。压比从1.05增长到1.6时,迷宫蜂窝密封流量系数升高约160%。

(2)迷宫蜂窝密封在小密封间隙和小压比时比光滑面迷宫密封更具优势;高低齿与台阶结构对流体的阻碍作用明显,流量系数随径向间隙增大而略有降低,流量系数最多降低了约10%。

(3)迷宫蜂窝密封流量系数随转速的增加而降低,当转速高于3 000 r/min时,流量系数明显下降;在间隙为0.6 mm、压比为1.05时,转速从0转速升高到8 000 r/min时,密封流量系数降低了51%;在高转速时孔中流体耗散加强,使迷宫蜂窝密封泄漏性能优于光滑面迷宫密封。

(4)迷宫蜂窝密封流量系数随蜂窝孔径增大先减小后升高,在孔径(0.6 mm)与齿宽相等时流量系数最低,此时流量系数比光滑面迷宫密封低3.0～5.5%;孔径小于1.6 mm时,迷宫蜂窝密封的泄漏特性优于光滑面迷宫密封。