等边三角形的拓展探究
江苏盐城市大丰区万盈初级中学(224100)王 刚
等边三角形是初中阶段学习的重要三角形,等边三角形既是等腰三角形,又是正多边形,是一种完美的三角形。等边三角形三边相等,三个角相等。等边三角形是拥有三条对称轴的轴对称图形,同时也是旋转对称图形,绕中心点至少旋转120°后能与自身重合。几何图形的拓展探究是近几年中考数学命题的方向之一,此类题常作为中考数学的压轴题,它一方面考查学生对几何图形的性质的掌握情况,另一方面考查学生的探究能力。此类题常与旋转、平移、翻折等图形变换相结合,探索角度、线段的数量关系、线段长和图形的形状等。
一、探索图形变化中的角度
在图形的形状、平分某一个角、垂直或平行关系、某条线段的中点等原始条件不变的情况下,随着某一条直线或一个动点处于不同的位置(如在图形的内部、边上或外部等),图形发生了变化,而其中某个角的角度始终不变,这就是变化中不变的量,在等边三角形中就存在这种情况。
[例1]△ABC是等边三角形,P为平面内的一个动点,BP=BA,0° <∠PBC<180°,DB平分∠PBC,且DB=DA。
(1)当BP与BA重合时(如图1),求∠BPD的度数;

图1
(2)当BP在∠ABC的内部时(如图2),求∠BPD的度数;
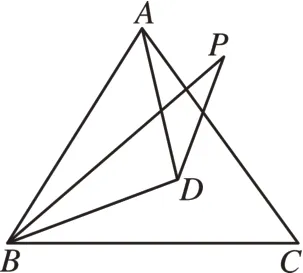
图2
(3)当BP在∠ABC的外部时,请你直接写出∠BPD的度数。
解析:(1)∵△ABC是等边三角形,BD平分∠PBC,∴∠PBD=∠CBD=30°,∵DB=DA,∴∠PBD=∠BPD=30°。
(2)连接CD,由“SAS”可证△PBD≌△CBD,可得∠BPD=∠BCD,由“SSS”可证△BCD≌△ACD,可得∠BCD=∠ACD==30°,即可求解。如图3,连接CD,∵点D在∠PBC的平分线上,∴∠PBD=∠CBD,∵△ABC是等边三角形,∴BA=BC=AC,∠ACB=60°,∵BP=BA,∴BP=BC,∵BD=BD,∴△PBD≌△CBD(SAS),∴∠BPD=∠BCD,∵DB=DA,BC=AC,CD=CD,∴△BCD≌△ACD(SSS),∴∠BCD=∠ACD==30°,∴∠BPD=30°。
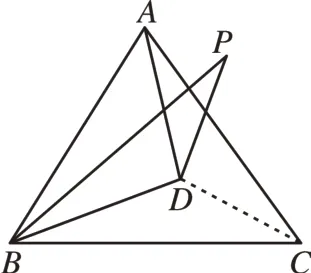
图3
(3)分三种情况进行讨论,由全等三角形的性质可求解。
如图4,连接CD,∵AD=BD,CD=CD,BC=AC,∴△ACD≌△BCD(SSS),∴∠ACD=∠BCD=30°,∵BD=BD,∠PBD=∠CBD,PB=BA=BC,∴△PBD≌△CBD(SAS),∴∠BPD=∠BCD=30°。

图4
如图5,连接CD,∵AD=BD,CD=CD,BC=AC,∴△ACD≌△BCD(SSS),∴∠ACD=∠BCD=30°,∵BD=BD,∠PBD=∠CBD,PB=BA=BC,∴△PBD≌△CBD(SAS)∴∠BPD=∠BCD=30°。
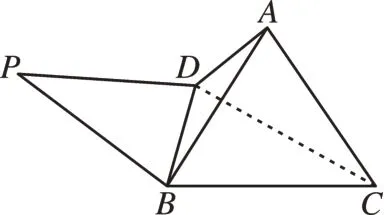
图5
如图6,连接CD,∵AD=BD,CD=CD,BC=AC,∴△ACD≌△BCD(SSS),∴∠ACD=∠BCD==150°,∵BD=BD,∠PBD=∠CBD,PB=BA=BC,∴△PBD≌△CBD(SAS),∴∠BPD=∠BCD=150°。
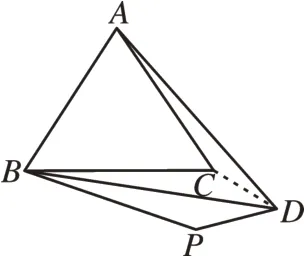
图6
评注:虽然线段BP相对于△ABC的位置发生了5 种变化,但是∠BPD的度数在前4 种图形中都没有发生变化,只在第5 种图形中发生了变化,其原因在于题中的原始条件:DB平分∠PBC,PB=BA,DA=DB始终不变。解题的思路都是一样的,都分别利用了“SSS”“SAS”证明两个三角形全等。
二、探究图形变化中线段的数量关系
在“手拉手”模型中,有一个顶点重合的一大一小两个等边三角形,将不重合的两个顶点分别联结,无论两个等边三角形如何旋转,都可以利用全等三角形得到联结所得的两条线段相等。在“角含半角”的模型中,一个角是另一个角的一半,且这两个角的顶点重合,无论这两个角如何旋转,都可以利用全等三角形得到一条线段等于另两条线段的和。
[例2]如图7,在△ABC中,∠ABC=∠ACB=60°,△BDC是等腰三角形且BD=CD,∠BDC=120°,以D为顶点作∠MDN=60°,交边AB,AC于M,N两点,延长AC到点E,使得CE=BM,连接MN,DE。

图7
(1)试说明:①△MBD≌△ECD;②MN=BM+NC;
(2)若点M是AB的延长线的一点,N是CA的延长线上的点,点E在线段AC上,其他条件不变,探究线段BM,MN,NC之间的关系,并说明理由。
解析:(1)①如图8,延长AC至E,使得CE=BM,并连接DE。∵△BDC为等腰三角形,△ABC为等边三角形,∴BD=CD,∠DBC=∠DCB,∠MBC=∠ACB=60°,又BD=DC,且∠BDC=120°,∴∠DBC=∠DCB=30°,∴∠ABC+∠DBC=∠ACB+∠DCB=60°+30°=90°,∴∠MBD=∠ECD=90°,在△MBD与△ECD中,∵BD=CD,∠MBD=∠ECD,EC=BM,∴△MBD≌△ECD(SAS)。

图8
②∵△MBD≌△ECD(SAS),∴MD=DE,∠BDM=∠CDE,BM=CE,又∵∠BDC=120°,∠MDN=60°,∴∠BDM+∠NDC=∠BDC−∠MDN=60°,∴∠CDE+∠NDC=60°,即∠NDE=60°,∵∠MDN=∠NDE=60°,在△DMN与△DEN中,DM=DE,∠MDN=∠NDE,DN=DN,∴△DMN≌△DEN(SAS),∴MN=EN,又∵NE=NC+CE,BM=CE,∴MN=BM+NC;
(2)结论:MN=NC−BM。
理由:如图9,在CA上截取CE=BM。∵△ABC是正三角形,∴∠ACB=∠ABC=60°,又∵BD=CD,∠BDC=120°,∴∠BCD=∠CBD=30°,∴∠MBD=∠DCE=90°,在△BMD和△CED中,∵EC=BM,∠MBD=∠DCE,BD=DC,∴△BMD≌△CED(SAS),∴DE=DM,在△MDN和△EDN中,∵ND=ND,∠EDN=∠MDN,MD=ED,∴△MDN≌△EDN(SAS),∴MN=NE=NC−CE=NC−BM。
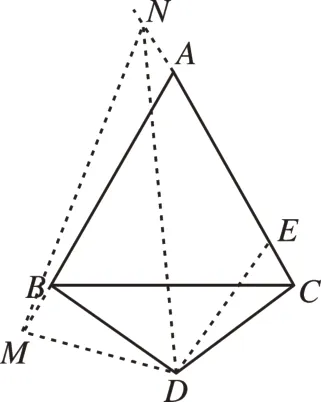
图9
评注:已知或求证一条线段等于另两条线段的和,一般采用“截长补短法”,即在较长线段上截取一条线段,使之等于其中一条较短线段,然后通过三角形全等得到截剩下的线段等于另一条线段,或者将其中一条较短的线段延长,使延长部分的线段等于另一条较短线段,然后通过三角形全等得到延长后的线段等于长线段。
三、探究图形变化中三角形的形状
在等边三角形每边依次取相等的线段,分别联结这三个“分点”与对角顶点形成三条线段,这三条线段围成的三角形是等边三角形,或者在等边三角形每边依次取相等的线段,顺次联结这三个“分点”所得的三角形仍是等边三角形;两个大小不等的等边三角形,其中一个顶点重合,然后将不重合的两个顶点联结,得到两条线段,再取两条线段的中点,两中点与重合的顶点形成的三角形仍是等边三角形。
[例3]如图10,△ABC,△CDE都是等边三角形,AD,BE相交于点O,点M,N分别是线段AD,BE的中点。

图10
(1)求证:△ACD≌△BCE;
(2)求∠DOE的度数;
(3)试判断△MNC的形状,并说明理由。
解析:(1)根据等边三角形性质得AC=BC,CD=CE,∠ACB=∠DCE=60°,根据“SAS”即可证明△ACD≌△BCE。
∵△ABC,△CDE都是等边三角形,∴AC=BC,CD=CE,∠ACB=∠DCE=60°,∴∠ACB+∠BCD=∠DCE+∠BCD,∴∠ACD=∠BCE,在△ACD和
∴△ACD≌△BCE(SAS)。
(2)根据全等求出∠ADC=∠BEC,根据三角形的内角和定理求出∠ADE+∠BED的值。
∵△ACD≌△BCE,∴∠ADC=∠BEC,∵△DCE是等边三角形,∴∠CED=∠CDE=60°,∴∠ADE+∠BED=∠ADC+∠CDE+∠BED=∠ADC+60° +∠BED=∠CED+60°=60°+60°=120°,∴∠DOE=180° −(∠ADE+∠BED)=60°。
(3)求 出AM=BN,根 据“SAS”证△ACM≌△BCN,推出CM=CN,求出∠NCM=60°。
∵△ACD≌△BCE,∴∠CAD=∠CBE,AD=BE,AC=BC,又∵点M,N分别是线段AD,BE的中点,∴AM=AD,BN=BE,∴AM=BN,在△ACM和△BCN中,AC=BC,∠CAM=∠CBN,AM=BN,∴△ACM≌△BCN(SAS),∴CM=CN,∠ACM=∠BCN,又∠ACB=60°,∴∠ACM+∠MCB=60°,∴∠BCN+∠MCB=60°,∴∠MCN=60°,∴△MNC是等边三角形。
评注:在解答第(2)问的过程中,使用了“8”字形图形,因为对顶角相等,根据三角形内角和为180°,可得剩下的两个角的和相等。判定一个三角形的形状,一般考虑它可能为等腰三角形、等边三角形或直角三角形。根据三角形的大致形状,要判断一个三角形为等边三角形,一般通过“有一个角是60°的等腰三角形是等边三角形”来判定。
等边三角形的拓展探究,还包括探究图形变化中线段的长、探究图形变化中的内接正三角形。它们都是以等边三角形为背景,构造图形的变化、运动,在图形的变化过程中,探究其中不变的量,如角度、数量关系或图形形状等,一方面考查学生的画图能力,另一方面考查学生的知识迁移能力,以及考查学生能否利用相同的方法解决不同的问题。

