几何画板与初中数学教学有效融合的探索

广西南宁市第三中学初中部青秀校区（530029）廖小舟

随着现代信息技术的不断发展，初中数学的教学方式也随之发生了新变化，教学方法更加多样化。在数学教学中，现代信息技术越来越得到重视，逐渐成为学生学习数学知识和解决数学问题的强有力的工具。几何画板是一种强有力的可视化动态软件，它能有效促进学生学习数学，改变学生的数学学习方式，对初中数学的教与学都产生了深远的影响。在初中数学教学中，教师可有效应用几何画板辅助教学，创设多种有助于学生思考、观察的问题情境，充分调动学生学习的主动性和积极性，活跃学生的思维，提升学生的动手操作能力。本文主要讨论几何画板在数学概念、数学图像的教学和数学问题解决中的作用及其在初中数学教学中的应用。

一、几何画板在数学概念教学中的作用

一般来说，数学概念的形成是一个抽象的过程，传统的教学方法不能将这个抽象的过程具体化和形象化，学生无法深入理解概念，更不能很好地把握概念的本质。而几何画板可以将静态转化为动态，将抽象转化为具体，能够清晰、直观地“展示”概念的抽象过程。借助几何画板，学生可以进行观察、思考、比较和分析，增强了学生对概念本质的理解。

例如，对于“三角形的中位线”这一内容，教材大多是直接给出相关的概念，使得学生学习和理解概念时产生了不少疑惑。借助几何画板，可以使教学过程更加形象。如图1，当点P在BC边上运动时，线段AP的中点Q的运动轨迹是怎样的呢？借助几何画板的动画功能，学生可以直观地看到动点Q在线段MN上来回运动，线段AP的所有中点轨迹的点正好形成三角形的中位线MN。通过观察，学生很容易理解中位线的概念，而且对中位线概念的形成也有深刻的认识。

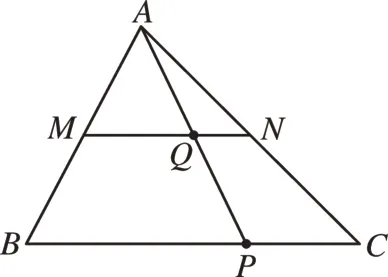
图1

二、几何画板在展示知识间联系时的作用

（一）可以准确展示不同概念间的联系

例如对于圆的切线，在传统教学中，学生往往只是停留在对教材概念“直线与圆有且只有一个交点时，该直线即为圆的切线”的文字理解上，而若应用几何画板的动态功能来展示圆的割线到圆的切线的变化，则能很好地揭示圆的割线与切线之间的区别与联系。这样，学生在学习圆的切线性质与判定时，就会更加清楚它们之间的内在联系，而且学生学习其他曲线的切线时也都可以通过类似的关系去理解。

（二）能形象展示一些性质定理间的联系

例如，在探索等腰三角形“三线合一”这一性质时，借助几何画板的移动功能，不仅能让学生充分认识到等腰三角形的特殊性，还丰富了学生的感性认识。如图2，在△ABC中，BA=BD，点C可以在AD延长线上移动，AC边上的高BP、中线BN和∠ABC的平分线BM是三条不同的线段，当点C在靠近点D运动时，△ABC由不等边三角形逐渐向等腰三角形转化，中线BN及角平分线BM随着点C的移动也不断向高BP“靠近”，直至与高BP重合。这样的动态过程能更好地帮助学生理解等腰三角形“三线合一”这一特殊性质的由来。

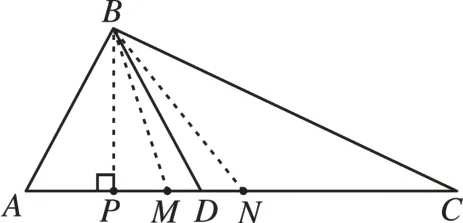
图2

三、几何画板在初中数学教学中的应用

（一）几何画板在代数教学中的应用

“多个绝对值之和的最值问题”是初中数学比较难的内容，学生感到非常抽象，难以入手。应用几何画板的度量功能，能帮助学生直观、形象地进行求解。教师应进一步启发学生分析、探索这类问题的一般求解方法，从而使学生认识到这类问题的本质。

［例1］如图3，一条街道旁有A，B，C，D，E五幢居民楼。某大桶水经销商统计各幢楼内居民每周所需大桶水的数量如下表。

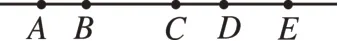
图3

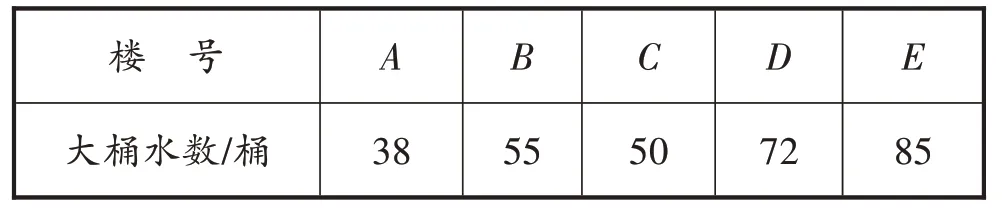
该经销商计划在这五幢楼中租一间房，设立大桶水供应点。若要使这五幢楼内的居民取水所走路程之和最小，那么可以选择的地点应在什么地方？

经讨论，学生给出了如下方案。

设AB=a，BC=b，CD=c，DE=d。每户居民每次取一桶水。

（1）若以点A为取水点，则五幢楼内的居民取水所走路程之和为55AB+50AC+72AD+85AE=262a+207b+157c+85d。

（2）若以点B为取水点，则五幢楼内的居民取水所走路程之和为38AB+50BC+72BD+85BE=38a+207b+157c+85d。

（3）若以点C为取水点，则五幢楼内的居民取水所走路程之和为38AC+55BC+72CD+85CE=38a+93b+157c+85d。

（4）若以点D为取水点，则五幢楼内的居民取水所走路程之和为38AD+55BD+50CD+85DE=38a+93b+143c+85d。

（5）若以点E为取水点，则五幢楼内的居民取水所走路程之和为38AE+55BE+50CE+72DE=38a+93b+143c+215d。

故以点D为取水点，五幢楼内的居民取水所走路程之和最小。

这时，笔者再提出问题：如果将“该经销商计划在这五幢楼中租一间房，设立大桶水供应点”改为“该经销商计划在这条街道上租一间房，设立大桶水供应点”，那么可以选择的地点在什么地方？

一石激起千层浪，学生给出了各种各样的答案，而且争论激烈，互不相让。笔者告诉学生，可以应用几何画板的度量功能和计算功能来探究这个问题。

如图4，在该直线上任取一个点P，选择度量距离，在绘图区显示出度量出来的长度，可以得到PA，PB，PC，PD，PE的长度。拖动点P，随着点P位置的变化，PA，PB，PC，PD，PE的值和38PA+55PB+50PC+72PD+85PE的值都在改变。当点P与点D重合时，38PA+55PB+50PC+72PD+85PE的值最小。因此，如果将“该经销商计划在这五幢楼中租一间房，设立大桶水供应点”改为“该经销商计划在这条街道上租一间房，设立大桶水供应点”，则在D处设立大桶水供应点，五幢楼内的居民取水所走路程之和最小。

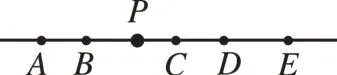
图4

这时，有学生提出问题：如果将某幢楼居民每周所需大桶水的数量改动一下，结论还一样吗？

可重新编辑该运算，如果将E幢楼居民每周所需大桶水的数量改为22桶，即PE前的数量由85改为22，拖动点P，结果发现，当点P与点C重合时，38PA+55PB+50PC+72PD+22PE的值最小。

学生一下子兴奋起来，跃跃欲试。于是，笔者让学生自由修改其中的数据，然后改变点P的位置，告诉大家所发现的结论。

当一个学生将PE前的数量85改为71后，学生沸腾了，他们发现当点P位于点C和点D之间（含点C，D）时，38PA+55PB+50PC+72PD+71PE的值保持不变，而且最小。这时，学生充满了好奇，他们很想知道到底是怎么一回事。

于是，笔者便从|x−3 |+|x−5 |的最小值谈起。由绝对值的几何意义知，|x−3 |和|x−5 |在数轴上分别表示x到3和x到5的距离。在x轴上任取一点x作为动点，仿照上一环节中的步骤，即可研究|x−3|+|x−5 |的最小值。仿照|x−3 |+|x−5|最小值的研究方法，再探究|x−3 |+|x−5 |+|x−2|，|x−3 |+|x−5 |+|x−2 |+|x+1|，|x−3 |+|x−5 |+|x−2 |+|x+1|+|x+7 |的最小值。结合数轴、绝对值的几何意义等相关知识，学生很快发现了如下规律。

若a1≤a2≤a3≤…≤an−1≤an，对于|x−a1|+|x−a2|+|x−a3|+…+|x−an−1|+|x−an|。

（1）若n为奇数，则当x=an+1时，原式有最小值。

（2）若n为偶数，则当an≤x≤an+1时，原式有最小值。

至此，学生恍然大悟。原来例1 中的街道相当于数轴，A，B，C，D，E五幢楼则是数轴上的点a1，a2，a3，a4，a5。要计算设立大桶水供应点的位置，使得五幢楼内的居民取水所走路程之和最小，则相当于在数轴上寻找点x，使38|x−a1|+55|x−a2|+50|x−a3|+72|x−a4|+85|x−a5|的值最小。这样，此类问题的本质得到了很好的揭示。

（二）几何画板在几何教学中的应用

几何画板为学生自主探索和自主学习提供了一个很好的平台，它是学生进行研究性学习的强有力的工具。教师应教会学生应用几何画板画图分析、探索思考、合作交流，让学生亲历知识的产生与形成过程，使“知识”发现、“方法”习得与“态度”形成达到高度统一，从而实现知识的自主建构。

近年来，一类以“链式”问题形式出现的几何探究题可谓精彩纷呈，命题者充分考虑到学生的认知规律，让学生在一定的情境中完成探究，使学生的才能得到充分的展示，因此此类探究题成为中考数学的一大亮点。这类探究题往往缺少一定的条件或无明确的结论，需要经过推断、补充并加以证明。根据其特征大致可分为条件探究题、结论探究题、规律探究题和存在探究题等。探究题的知识覆盖面较大，综合性较强，灵活选择方法的要求较高，再加上题意新颖、构思精巧，具有相当的深度和难度。

［例2］如图5，点A为等边三角形BCE内任一点，以AB为一边作等边三角形ABD，连接DE，AC，则图中哪两个三角形全等？请说明理由。

图5

学生容易发现并证明△ABC≌△DBE，然后以AC为一边作等边三角形ACF，连接EF（如图6），同理可证△ABC≌△FEC。这时，教师提出问题，并进行师生交流。

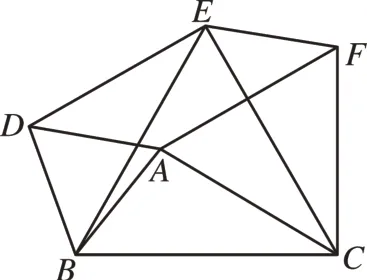
图6

师：除全等三角形外，你还发现了什么结论？你能说明其中的道理吗？

生1：四边形AFED是平行四边形。易得△ABC≌△DBE和△ABC≌△FEC，所以△DBE≌△FEC，所以EF=DB=AD，DE=FC=AF，用“两组对边分别相等的四边形是平行四边形”可证。

师：拖动点A，改变它在△BCE中的位置，有什么发现？

生2：四边形AFED还有可能是矩形、菱形、正方形。

师：当△ABC满足什么条件时，会出现上述情形？

生3：只要△ABC满足∠BAC=150°，四边形AFED就是矩形。

师：你是怎么探索的？

生4：因为四边形AFED是平行四边形，所以要使四边形AFED是矩形，只要有一个角等于90°或对角线相等即可。而点A是△ABC与四边形AFED的公共点，分析与点A相关的元素。四边形AFED与△ABC相关的角是∠DAF，只要使∠DAF=90°即可，△ABC只要满足∠BAC=360° −90° −2 ×60°=150°即可。

很快，学生的兴趣被激发了，有学生发现，要使四边形AFED是正方形，首先要保证它为矩形，即△ABC满足∠BAC=150°，而这样的点A有无数多个，同时还应满足“邻边相等”，而四边形AFED与△ABC相关的邻边为AD，AF，所以只要AD=AF即可，而AD=AB，AF=AC，需要再补充AB=AC这个条件，所以当△ABC满足AB=AC且∠BAC=150°时，四边形AFED是正方形。

在探索当△ABC满足什么条件，四边形AFED是菱形时，学生首先进行了分析和猜想：在上面正方形的探索中，当△ABC满足AB=AC时，AF=AC一定成立，这时四边形AFED是菱形。

生5：在操作几何画板寻找满足条件的点A的位置时，总是很难精准地找到相应的位置，不知有什么办法？

生6：因为点A满足AB=AC，且点A在△BCE内，所以点A的轨迹为线段BC的中垂线在△BCE内的那一部分，那么作线段BC的中垂线EM，在线段EM（不含端点E）上的任何一点均可使四边形AFED是菱形。

由于学生的知识限制，对于使四边形AFED是矩形及正方体时，找点的精确位置需要进行详细的讲解。因为△ABC满足∠BAC=150°，而“同弧所对的圆周角相等”，所以只要找到一个特殊点N，使∠BNC=150°，劣弧BNC即为所求点A的轨迹，将点A与劣弧BNC合并即可。

通过上述分析与操作，学生发现点A的运动引起△ABC的形状发生变化，进而使得四边形AFED变成不同的形状。这样的课堂生动形象而又有趣，减少了教师画图的时间，提高了教学效率，激发了学生对数学问题的探究热情。

综上，数学课程的设计与实施应根据实际情况合理地运用现代信息技术，要注意信息技术与课程内容的整合，注重实效；要充分考虑信息技术对数学学习内容和方式的影响，开发并向学生提供丰富的学习资源，把现代信息技术作为学生学习数学和解决问题的有力工具，有效地改进教与学的方式，使学生乐意投入到探索性的数学活动中去。数学课程改革要反映信息技术所引发的变革，就必须将数学课堂教学与信息技术进行整合。几何画板在作图的过程中动态地保持了几何图形中内在的、恒定不变的几何关系及几何规律。利用几何画板可以按给定的数学规律和关系来制作图形（或图像、表格）。学生在通过观察、类比和分析提出问题后，还可以借助几何画板验证问题的真假，从而发现恒定不变的几何规律。

课堂教学魅力无穷、潜力巨大，结合信息技术，可使课堂教学精彩纷呈。几何画板具备强大的图形生成功能，弥补了传统教学手段的不足，大大提高了教学效率和教学效果，但课堂教学也不能由信息技术“牵”着走，教师应根据课程内容择优使用，不能太过依赖信息技术。信息技术的本质是辅助教学，几何画板的使用应以提高学生学习兴趣、引发学生思考、提高学习效率为目的，让学生学会主动探究，理解概念和结论，知其所以然。