着眼全局 正本清源
——对高中“圆”的教学思考
江苏张家港市暨阳高级中学(215600)季芸洁
“圆”是学生最熟悉的基本平面几何图形之一,也是初、高中数学的重要内容。在具体的教学中,如果不能正确认识“圆”在初、高中数学中的地位,就会偏离正确的教学方向。下面是笔者的一些认识,供同行参考、指正。
一、教学现状
在高中数学教学中,部分教师延续初中对“圆”的教学要求,单纯强调“圆”的几何性质的学习和应用。例如,对于圆的定义,只介绍“到定点的距离为定值”这一种形式;对于直线与圆的位置关系,只说明利用“点到直线的距离与半径大小关系”来判断;对于点与圆的位置关系,只强调通过“点到圆心的距离”与“半径”的比较来分析。这些都是研究“圆”的重点方法,很多与“圆”有关的问题,利用这些几何性质可简洁求解。但是,初、高中数学对“圆”知识的学习侧重点不同,初中数学重视的是圆的几何性质的应用,而高中数学则将“圆”作为解析几何的基本内容,倾向于用解析法去研究、解决“圆”的相关问题。因此,在高中“圆”的教学中,既要突出圆的几何性,又要突出圆的代数性。
二、教学改进
在高中数学中,“圆”是解析几何的基础,是学生后续学习椭圆、双曲线、抛物线的基础,研究这些圆锥曲线的定义、方程以及直线与圆锥曲线的关系都要用到圆。
(一)引申圆的定义
在平面内到定点的距离等于定长的点的轨迹是圆。除这种定义外,还要引入其他形式的定义,为后期探究椭圆、双曲线、抛物线打下基础。
[例1]在平面直角坐标系xOy中,点A(−2,0),B(2,0),P是平面内的动点,且PA,PB斜率之积为−1,求点P的轨迹方程。

说明:圆的这种定义形式更能体现利用定义法求曲线方程的基本思路,即求点的轨迹方程,就设点的坐标为(x,y),再根据题目条件找到x,y的关系,要注意排除不符合条件的点。
[例2]在△ABC中,AB=2,AC=BC,求点C的轨迹方程。
解析:如图1 所示,以AB的中点O为坐标原点,AB所在的直线为横轴,建立平面直角坐标系。
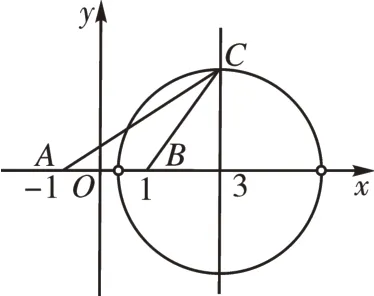
图1

说明:圆的这种定义形式可以简记为“到两个定点的距离之比为定值的点的轨迹,且定值不为1”。在这一定义形式下的圆也称为“阿波罗尼斯圆”。以此为背景的命题在近年的高考试卷中屡见不鲜。
[例3]在平面直角坐标系中,点P(cosθ,sinθ)到直线x−my−2=0 的距离为d。当θ,m变化时,dmax=__________。
解析:假设x=cosθ,y=sinθ,则P(cosθ,sinθ)的轨迹方程为x2+y2=1,即为单位圆,圆心到x−my−2=0的距离为
如图2 所示,圆x2+y2=1上 的 点P(cosθ,sinθ) 到x−my−2=0 的距离的最大值为,即m=0,dmax=3。
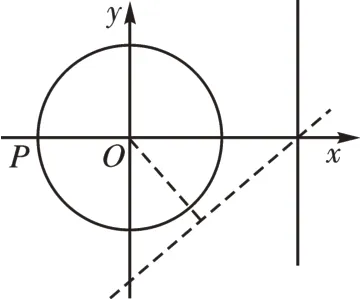
图2
说明:圆心为点(a,b),半径为r的圆的参数方程(θ为参数),此类问题可借助圆的参数方程、三角函数的性质处理。
(二)拓展问题的处理方法
处理椭圆、双曲线综合问题的基本方法有坐标法、代入消元法、判别式法,因此教师在“圆”的教学中也要引导学生掌握这些方法。例如在处理直线与圆的位置关系问题时,教师除了讲解几何法,还要介绍代数法,即将直线方程与圆的方程联立,代入消元得到含x或y的一元二次方程,进而利用判别式及根与系数的关系,整体代换、设而不求解决问题。
[例4]已知方程x2+y2−2x−4y+m=0。
(1)若此方程表示圆,求m的取值范围;
(2)若(1)中的圆与直线x+2y−4=0 相交于A,B两点,且原点O在以AB为直径的圆内,求m的范围。
解析:(1)由(−2)2+(−4)2−4m>0,即4+1 −m>0,解得m<5。
(2)将直线x+2y−4=0与圆的方程x2+y2−2x−4y+m=0联立,消元得(4 −2y)2+y2−2(4 −2y)−4y+m=0,整理得5y2−16y+8 +m=0,由Δ=(−16)2−20×(8+m)>0,解得m<


[例5]如图3,已知圆C:x2+(y−3)2=25 与x轴的负半轴相交于点M。过点M作MA,MB分别与圆C相交于点A,B,且直线MA,MB关于x轴对称,试问直线AB的斜率是否为定值?若是,请求出这个值;若不是,请说明理由。
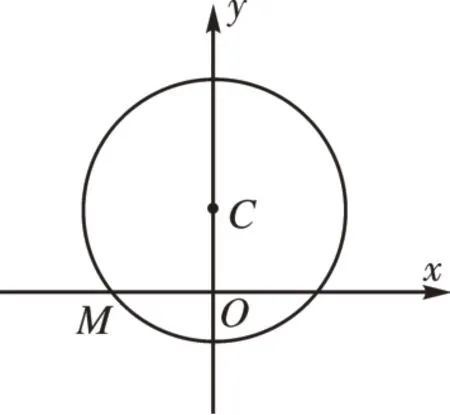
图3

说明:本题也可以采用几何法求解。如图4,设圆与x轴的正半轴相交于点M′。由MA,MB关于x轴对称可知,∠AMM′=∠BMM′,所 以M′为的中点,连接CM′,则CM′⊥AB,因为直线CM′的斜率为所以kAB=即直线AB的斜率为定值。几何法虽然简洁,但代数法的意义更为重大。
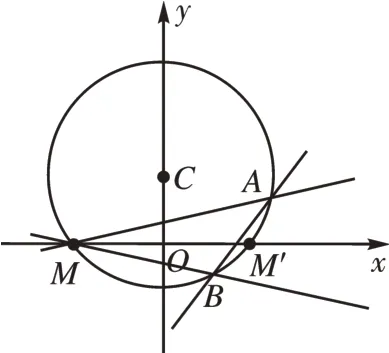
图4
[例6]如图5 所示,在直角坐标系xOy中,已知圆O:x2+y2=4,点B,C在圆O上,且关于x轴对称。
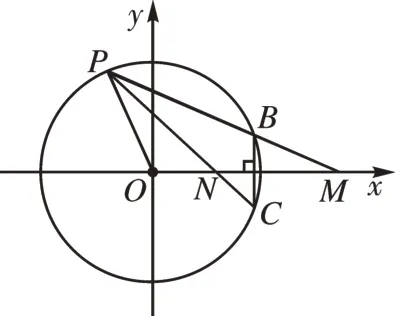
图5
(1)当点B的横坐标为的值;
(2)设P为圆O上异于B,C的任意一点,直线PB,PC与时,求x轴分别交于点M,N,证明:|O M|·|ON|为定值。
解析:(1)略;

说明:上述求解体现了解决解析几何问题的另外一种重要方法,即“设点法”。题目中动态问题的背景是由动点P引起的,故可设出点P的坐标,再将其他相关点的坐标用点P的坐标表示出来,结合题目条件列出相应的关系式,再借助点P在曲线上,利用曲线方程进行消元。这种方法也是处理圆锥曲线问题的重要方法。因此,教师在“圆”的教学过程中要体现这一方法的应用。另外,对本题进行深入探究不难发现该定值即为圆的半径的平方,感兴趣的读者可自行进行证明。
(三)落实圆的应用
高考命题中既有直接考查圆的题型,又有以圆为解题工具进行间接考查的题型,即通过构造圆的模型来解决问题。因此,在教学中教师要落实圆的应用。
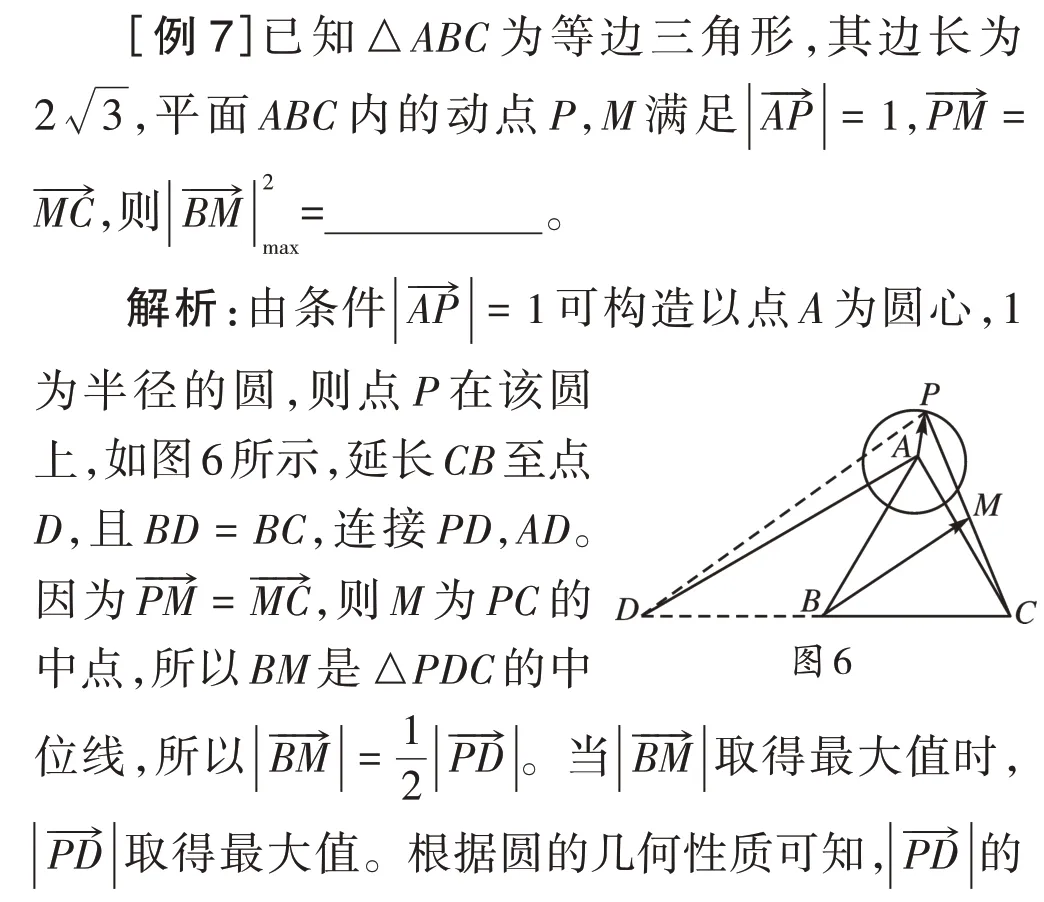

说明:本题条件中并没有出现圆,但结合向量的模为定值,可构造以向量的模为半径的圆,从而利用圆的几何性质简洁求解。

说明:整体来看,圆的方程不是函数,但从局部来看,单位圆x2+y2=1 在x轴上方的部分可表示为y=,进而转化为函数,可利用函数的知识方法来研究圆。类似地,y=表示单位圆在x轴下方的部分。
三、教学反思
高中数学教材中各模块所处的位置并不是独立的,前后之间都具有一定的关联,特别是2019 年人民教育出版社出版的新教材,各模块之间的顺序更严谨,新教材将圆与椭圆、双曲线安排在一起,放置在选择性必修一中。因此在教学中,教师不能孤立地教学某一模块,应综合考虑本模块与前后模块之间的联系,为后一模块的学习奠定基础,为前面已学模块创造拓展的空间。

