基于偏最小二乘回归方法的毛管压力曲线预测超致密砂岩储层渗透率

郭一凡，司马立强，王 亮，郭宇豪

（1.西南石油大学地球科学与技术学院，四川成都 610500；2.西南石油大学油气藏地质及开发工程国家重点实验室，四川成都 610500；3.成都理工大学能源学院，四川成都 610059）

在川西坳陷南部深层、超深层须家河组致密砂岩储层中发现了丰富的油气资源［1］，证实川西地区深部致密砂岩领域具有十分巨大的天然气勘探潜力。岩石物性是评价储层性质的关键参数，中外学者多将孔隙度和渗透率作为砂岩储层的分类依据［2-3］，通常将孔隙度低于10%、渗透率低于0.1 mD的砂岩储层定义为致密砂岩储层。四川盆地勘探初期，王金琪发现须家河组三段（须三段）储层与同研究区致密砂岩储层的成藏机制有所不同且物性差异较大，为区分研究故将其定义为超致密砂岩储层［4］。赵澄林等参考美国致密砂岩储层评价方法将孔隙度低于3%、渗透率低于0.01 mD 的砂岩储层定义为超致密砂岩储层［5］。渗透率是评价储层的重要参数，超致密砂岩相较于致密砂岩、常规砂岩，渗透率更低，孔隙度与渗透率相关性更差，孔喉结构更复杂，且多发育纳米级孔喉及天然裂缝［6］。由于渗透率主要受控于孔隙结构［7-8］，通过高压压汞实验测定的毛管压力曲线可以较好地反映储层的孔喉特征［9-11］。因此，前人常利用高压压汞实验获取孔喉结构参数，进而构建渗透率预测模型［12］。

目前，基于毛管压力曲线的渗透率预测模型多根据Poiseuille’s 等式和Darcy 定律建立。例如PURCELL 于1949 年建立适用于砂岩储层的Purcell模型［12］；THOMEER 建立适用于砂岩储层的Thomeer模型［13-14］；KOLODZIE 于1980 年使用进汞饱和度为35%时对应的孔喉半径划分砂岩储层和碳酸盐岩储层的岩石物理类别并建立Winland-r35模型［15］。此后，其他学者如REZAEE 等对西澳致密砂岩气储层开展研究，发现进汞饱和度为10%时对应的孔喉半径与渗透率的关联性最高［16-17］；刘刚等认为鄂尔多斯盆地致密油储层预测渗透率的最佳孔喉半径为进汞饱和度为5%时对应的孔喉半径［18］；SWAN⁃SON 发现砂岩储层控制流体流动的有效孔喉临界值与双对数坐标系下的毛管压力曲线顶点对应，即Swanson 参数，经大量岩心数据分析证实Swanson 参数与渗透率存在幂函数关系［19-20］；PITTMAN 于1992年建立适用于砂岩储层的Pittman 模型［21］；GUO 等于2004 年提出Capillary-Parachor 参数也反映储层孔隙结构［22］；肖忠祥等于2008 年针对中国西部3 个油气田提出利用三次样条插值函数自动计算Capil⁃lary-Parachor 参数的新方法［23］。但上述传统模型多应用于常规砂岩储层和碳酸盐岩储层，在超致密砂岩储层中应用效果未知，且仅使用少量参数建立模型，并不能代表毛管压力曲线的全部信息。对渗透率影响因素多［24-25］、孔喉结构复杂的超致密砂岩储层迫切需要一种精度高、适用性强的渗透率预测模型。

为此，选取川西坳陷南部大邑构造须三段超致密砂岩储层岩心样品开展物性、高压压汞等实验，分析超致密砂岩渗透率的主控因素。分析经典渗透率预测模型存在预测误差的原因，采用留一交叉验证法（LooCV）和偏最小二乘回归方法，有效地解决了数据集样本较少、泛化能力弱、各参数的多重共线性拟合误差大、预测精度低的问题，研究成果可以为超致密砂岩油藏勘探开发提供借鉴与思路指导。

1 实验器材及方法

74 块岩心样品取自川西坳陷南部大邑构造，该构造发育于中三叠统海相褶皱盖层基底之上，为晚三叠世以来形成于深坳陷地带的前陆盆地［26-27］。地表出露上白垩统灌口组至新近系名山组红色碎屑岩和第四系大邑砾岩，地腹从浅至深依次为侏罗系红色碎屑岩和上三叠统暗色含煤碎屑岩［28］。须三段厚度为430～480 m，为含深灰色、灰黑色页岩夹薄煤层，浅灰色、灰白色厚层块状中-细粒岩屑石英砂岩、岩屑砂岩，深灰色、灰黑色页岩夹浅灰色、灰白色中厚层状中-细粒岩屑长石石英砂岩［29-30］。

氦气孔隙度测量采用非常规层孔渗分析仪CMS-300，根据波义尓定律，结合先进的标定技术，测试岩心孔隙度。渗透率测试基于Darcy 定律，即当气体的压力沿岩心样品长度的分布呈稳定状态时，样品轴向各点的气体压力只随位移变化而不随时间变化。高压压汞实验选用9500全自动压汞仪，由于汞为非润湿相，在外加压力作用下，汞克服毛管压力，可进入岩石孔隙；随着压力的增加，非润湿相流体汞优先进入较大的孔喉和连通性较好的孔喉，岩心样品中汞饱和度不断增加，可以得到注入压力与岩心样品中汞饱和度的关系曲线即为毛管压力曲线。实验流程严格遵循岩心分析方法和岩石毛管压力曲线的测定［31-32］。

2 实验结果分析

川西坳陷南部大邑构造须三段超致密砂岩岩心样品的物性实验结果（图1）显示，其孔隙度最低为0.39%，最高为4.5%，平均为2.86%，主要分布于1%～4.5%；渗透率最低为0.000 6 mD，最高为0.147 5 mD，平均为0.023 2 mD，主要分布于0.001～0.05 mD，属于超致密砂岩储层。研究区须三段超致密砂岩储层孔隙度与渗透率相关性差，非均质性强，即孔隙度相近的岩心样品渗透率差异明显。为确保实验研究更具代表性和工区适用性，选取12块渗透率差异较大的岩心样品开展高压压汞实验。

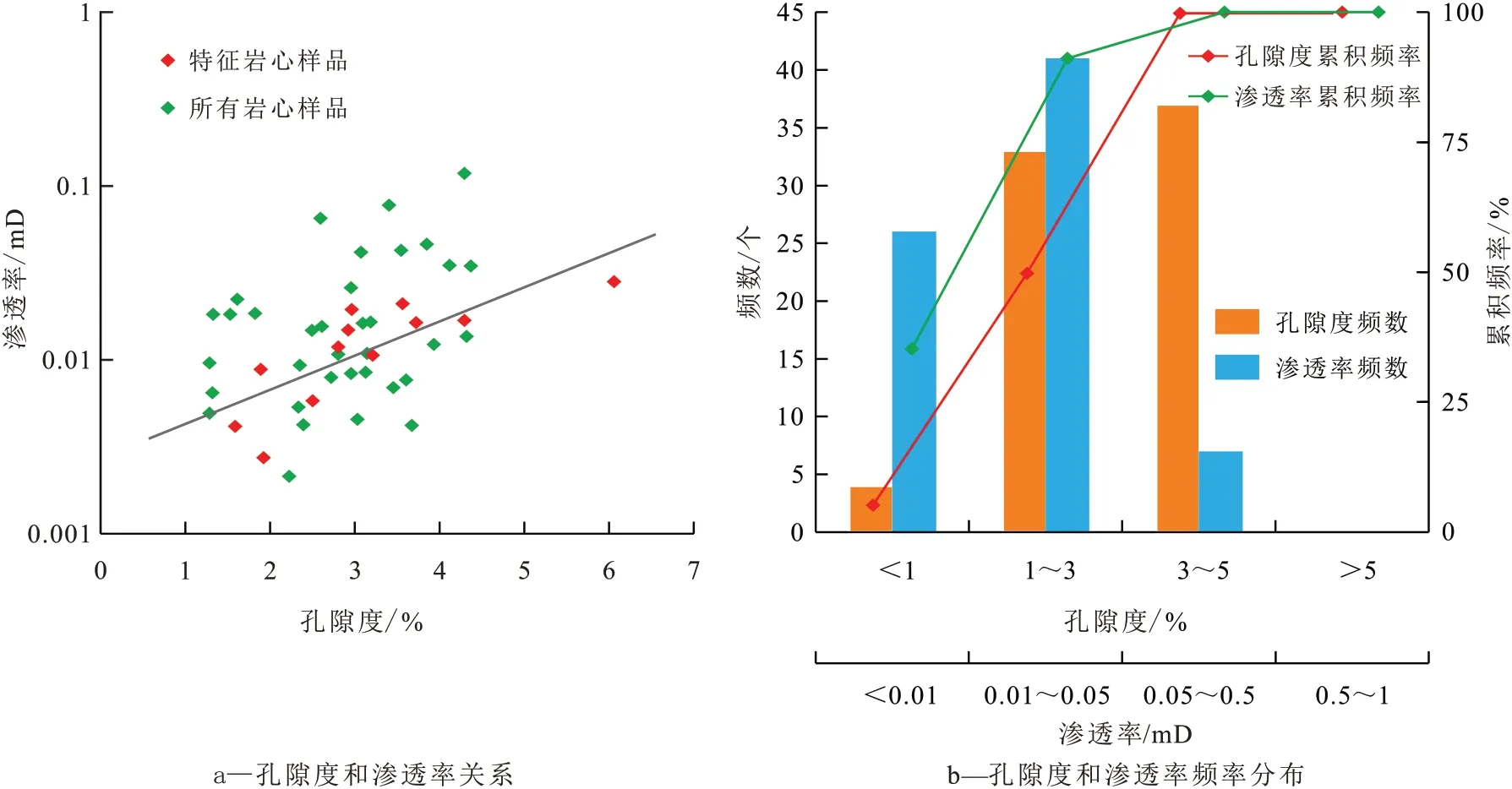
图1 川西坳陷南部大邑构造须三段超致密砂岩岩心样品物性实验结果Fig.1 Experimental results of physical properties of ultra-tight sandstone core samples from Third Member of Xujiahe Formation in Dayi structure of southern Western Sichuan Depression

对选取的12 块超致密砂岩岩心样品开展注入压力为200 MPa 的高压压汞实验，结果（图2）表明，研究区岩心样品毛管压力曲线平台性不明显，整体孔喉分布特征呈差分选、细歪度；排驱压力为1.355～8.263 MPa，平均为3.542 MPa；最大进汞饱和度为59.034%～74.231%，平均为63.723%；剩余汞饱和度为37.374%～46.160%，平均为44.622%。岩心样品孔径分布大致可分为单峰、双峰两类，孔喉半径主要分布于0.01～0.1 μm，少量分布于0.005～0.01 μm。12 块岩心样品孔喉结构以发育纳米、微米级的小孔隙为主，喉道细小且孔喉连通性差，导致汞残留在孔喉中［33-34］。通过高压压汞实验测试得到毛管压力曲线，可获得分选系数、歪度、均值半径、最大进汞饱和度和排驱压力等参数，进而可以计算得到经典渗透率预测模型参数。其中，Swanson参数的确定方法为过某点A作一条45°的直线，在不改变角度的情况下调整直线位置，至与双对数坐标轴下的毛管压力曲线相切，A 点为双曲线顶点即Swanson参数，即A点前非润湿相进入有效的连通孔喉空间，在A点后非润湿相进入更细小的孔喉空间，流动能力明显下降；以SHg为横坐标，SHg/pc2为纵坐标建立坐标系，其曲线最高点为（SHg/pc2）max，即为Capil⁃lary-Parachor 参数；选取Swanson 参数对应的孔喉半径rapex即为Pittman 参数；分别选取进汞饱和度为35%，10%和5%时对应的孔喉半径为Winland 模型的r35，r10和r5关键参数。以研究区2 号岩心样品在双对数坐标、特殊坐标轴下的毛管压力曲线为例，分别展示经典渗透率预测模型特征参数的确定方法，以及与渗透率的相关性分析，经统计拟合确定6种特征孔喉参数与渗透率均呈幂函数正相关，但总体相关性仍然不明显（图3）。

图2 川西坳陷南部大邑构造须三段超致密砂岩高压压汞实验结果Fig.2 High-pressure mercury intrusion test results of ultra-tight sandstone core samples from Third Member of Xujiahe Formation in Dayi structure of southern Western Sichuan Depression

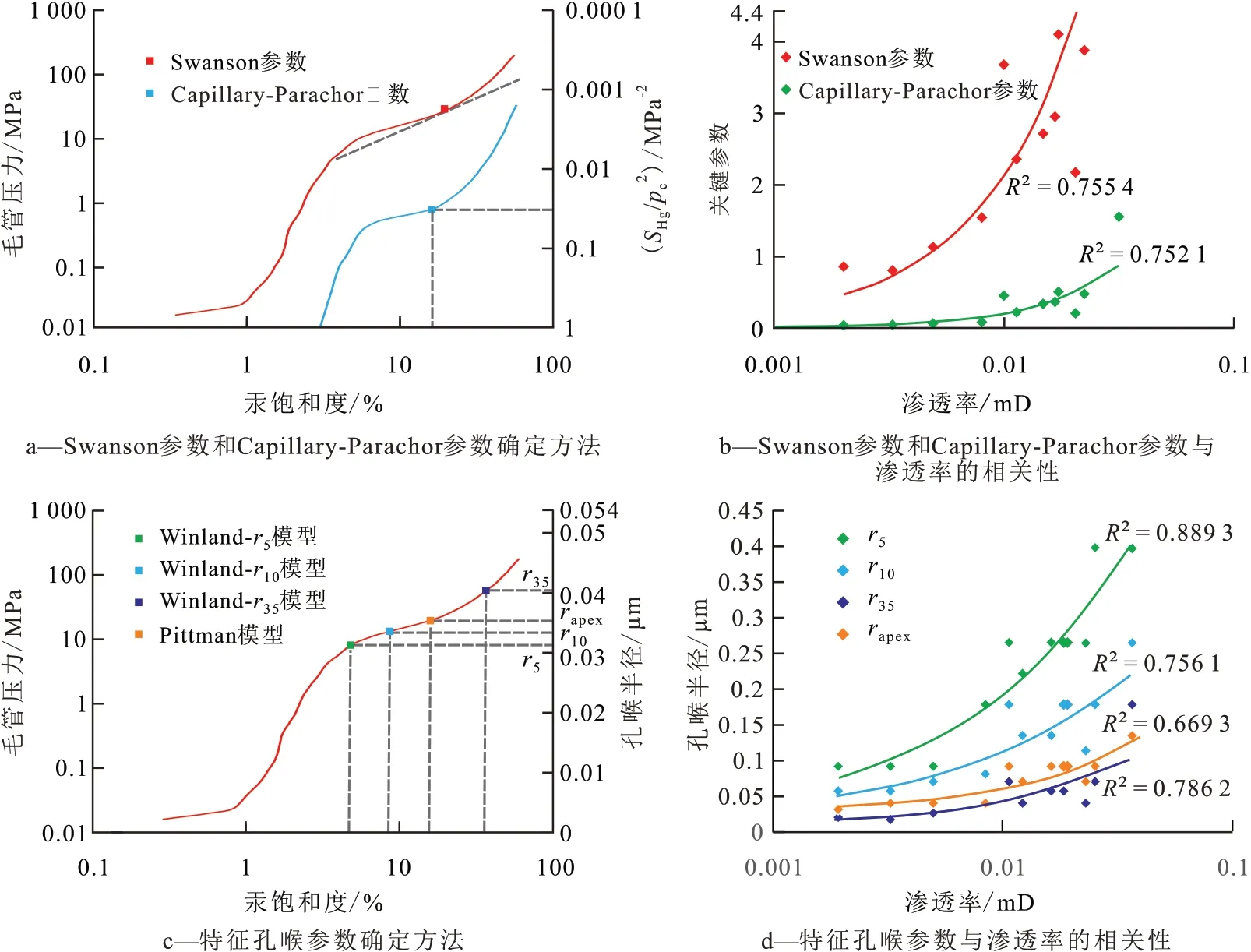
图3 川西坳陷南部大邑构造须三段2号岩心样品渗透率预测模型特征孔喉参数Fig.3 Parameters of characteristic pore throat in permeability prediction models for No.2 core sample from Third Member of Xujiahe Formation in Dayi structure of southern Western Sichuan Depression

3 经典渗透率预测模型误差分析

以均方根误差和相关系数作为评价渗透率预测模型的精度指标，且不同模型的自变量数并不相同，随着自变量数的增加，相关系数随之增加。为消除其影响以便于不同模型的相互比较，引入修正相关系数：

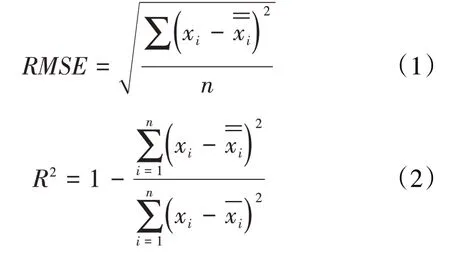
将经典渗透率预测模型中的特征参数进行基于普通最小二乘方法的多元线性回归后，分别得到研究区须三段超致密砂岩储层渗透率计算公式（表1）。引入均方根误差等参数来表征渗透率预测模型的预测精度。分析表明，经典渗透率预测模型的预测精度、拟合效果、修正效果均不理想，误差产生的原因总结为各类经典渗透率预测模型的关键参数的取值方法仍存在局限性，且在渗透率影响因素复杂的超致密砂岩储层中，采用单一参数并不能表征毛管压力曲线的全部信息，需增加其他参数共同表征毛管压力曲线的整体特征。具体分析误差原因为：①Thomeer 模型中，将等式两边同取对数后，不难看出该类毛管压力曲线在双对数坐标轴下对应为斜率为−1、截距为(lgpcd+1lgSHg∞)的线性回归方程。但超致密砂岩储层毛管压力曲线在双对数坐标轴下的曲线形态显然不符合这一规律。因此，Thomeer 模型并不适用于超致密砂岩储层［35］。②Swanson 模型和Capillary-Parachor 模型在研究区存在差异性和取值方法的局限性，这2 个模型均基于常规砂岩储层建立，对于超致密砂岩储层暂时无理论依据和实际检验。对于孔喉结构复杂的超致密砂岩储层，渗透率贡献并不均匀［36］，采用单一特征孔喉参数无法表征毛管压力曲线整体特征，且只有部分区间呈双曲线特征，采用传统方法寻找参数点受人为因素影响较大、取值速度慢，为关键参数的半定量计算带来了极大的困难，无法满足油田大规模的开发及应用。总的来说，这类模型适用于高孔渗且渗透率贡献均匀即双曲线特性明显的常规储层。③Winland 模型、Pittman 模型和Rezaee 模型均是基于KOLODZIE 提出的最大连通孔喉尺寸划分岩石物理类别这一思路［15］，在不同区块建立特征孔喉尺寸与渗透率的关系。经分析统计，该类方法对于超致密砂岩储层的渗透率预测效果不理想，但整体表现趋势为由砂岩储层过渡到超致密砂岩储层，特征孔喉半径逐渐减小且与渗透率相关性逐渐明显。

4 基于偏最小二乘回归方法的渗透率预测模型

针对经典渗透率预测模型预测精度低的误差分析，总体归为2类：①特征孔喉尺寸参数与渗透率贡献区间对应关系模糊；②超致密砂岩储层渗透率影响因素繁杂，单一特征参数不能表征毛管压力曲线的全部特征，需引入更多相关变量。为高效地解决问题，首先选取3 类经典渗透率预测模型Win⁃land-r5（OLS）模型、Pittman（OLS）模型、Swanson（OLS）模型需要的基本物理参数进行多重共线性分析（表2）。诊断结果中的方差膨胀因子是衡量多元线性回归模型中多重共线性严重程度的一种度量，表示回归系数估计量的方差与假设自变量间非线性相关时方差的比值。经分析经典渗透率预测模型中关键参数的方差膨胀因子均大于10，最高为Dm参数，其VIF值为3 578.07，表明各关键参数存在多重共线性问题。因此，采用普通最小二乘回归方法拟合渗透率预测模型需要的特征参数并不适用。

表1 基于高压压汞资料的经典渗透率预测模型及误差分析Table1 Classical permeability prediction models and error analysis based on high-pressure mercury intrusion data

表2 超致密砂岩毛管压力曲线基本物理参数多重共线性分析Table2 Multicollinearity analysis of basic physical parameters from capillary pressure curve of ultra-tight sandstone

4.1 偏最小二乘回归方法

偏最小二乘回归方法作为一种多元统计数据分析方法［37］，可以解决多样本分析中存在的变量多重相关的实际问题。该方法将主成分分析法、典型相关及多元线性回归分析有机地结合起来［38］，尤其适用于变量多重相关性、小样本等情况下的多对多的线性回归分析。设一组因变量(y1,y2,∙∙∙,yQ)和一组自变量(x1,x2,∙∙∙,xP)，为研究因变量和自变量的统计关系，观测N个样本点，分别在X=(xij)NP和Y=(yij)NQ提取成分因子t1和u1。为满足回归需求，提取的成分因子需满足尽可能携带各自矩阵变异信息，以及成分因子t1和u1相关程度达到最大［39］。偏最小二乘回归是通过迭代法的逐步回归：

在提取了第1对成分因子t1和u1后，分别实施X对t1的回归及Y对t1的回归。如果回归方程已达到满意的精度，则算法终止，其中c1和d1分别称为成分因子t1的荷载，分别代表X和Y的系数向量，E1和F1分别是回归模型的残差矩阵：

若残差矩阵F1中元素的绝对值近似为0，则说明第1 组成分因子建立的回归方程已满足精度需求。否则将利用X被t1解释后的残余信息以及Y被t1解释后的残余信息，分别代替X和Y重复第1 步的过程：

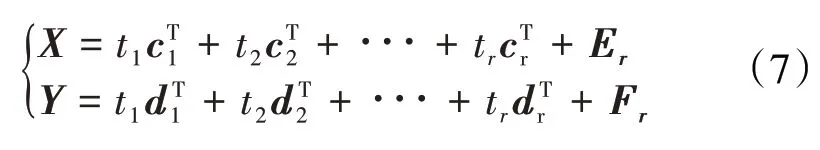
若最终对X共提取了r个成分因子(t1,t2,∙∙∙,tr)，即为标准化变量的线性组合，因此可以建立yk关于(x1,x2,∙∙∙,xP)的回归方程，即偏最小二乘回归方程。

4.2 关键参数计算

分析经典渗透率预测模型对超致密砂岩储层的适用性，在Winland-r5模型、Pittman 模型、Swanson模型的基础上，增加可以反映毛管压力曲线形态的分选系数、歪度以及排驱压力、孔隙度等参数共同作为预测模型的自变量，以期更完整的表征毛管压力曲线特征，渗透率作为因变量进行偏最小二乘回归方法分析。

在多数情况下，应用偏最小二乘回归方法建模并不需要对全部的成分因子进行回归分析，在建立模型前需通过交叉验证法确定X和Y的最优潜变量个数。笔者采用留一交叉验证法确定潜变量个数［40］，以判断某个主成分因子的引入是否对回归模型预测能力具有明显作用。其原理为：如果原始数据集有N个样本，将1 个样本独立作为验证集，其余的N-1 个样本作为训练集，进行原样本多数次抽取，至每个独立样本均已作为验证集。由于本批次岩心样品个数较少，使用常规交叉验证法无法验证模型泛化能力，因此留一交叉验证法为最佳选择。经MATLAB 软件计算确定最佳潜变量个数为2，即保留2 个主成分因子可代表整体数据集特性，以此为基础进行多参数偏最小二乘回归方法计算，具体结果见表3。

表3 川西坳陷南部大邑构造须三段超致密砂岩多参数偏最小二乘回归方法计算结果Table3 Results of parameters estimated by PLSR of ultra-tight sandstone sample from Third Member of Xujiahe Formation in Dayi structure of southern Western Sichuan Depression

4.3 应用效果

针对研究区须三段12 块超致密砂岩储层岩心样品，优选关键参数，开展偏最小二乘回归方法分析，建立渗透率预测模型。由预测效果（图4）可以看出，基于偏最小二乘回归方法建立的渗透率预测模型相比于普通最小二乘回归方法建立的模型，其相关系数和相关修正系数均有明显提高，尤其适用于Pittman 模型，拟合效果更好，对超致密砂岩储层的适用性更好。均方根误差值也有明显下降，Swan⁃son 模型的均方根误差值由1.52%降至0.36%，模型预测精度整体上升75%。预测结果显示，基于偏最小二乘回归方法的Winland-r5（PLSR）模型、Pittman（PLSR）模型、Swanson（PLSR）模型的渗透率预测结果相对较好，为后期超致密砂岩储层开发打下了坚实基础。

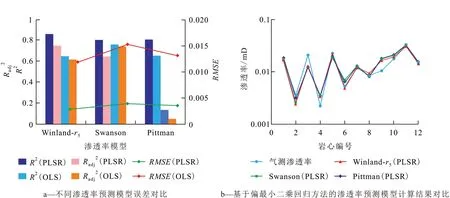
图4 川西坳陷南部大邑构造须三段超致密砂岩储层渗透率预测模型应用效果对比Fig.4 Application effect comparison of prediction models for ultra-tight sandstone reservoirs permeability of Third Member of Xujiahe Formation in Dayi structure of southern Western Sichuan Depression

5 结论

针对川西坳陷南部大邑构造须三段12 块超致密砂岩储层岩心样品，分析6 种经典渗透率预测模型的适用性和局限性，认为影响渗透率预测精度的主要原因为不同关键参数存在多重共线性问题，且单一参数不能完全表征孔喉结构特征。研究发现影响超致密砂岩储层渗透率的主要因素为孔隙度、有效孔喉半径区间、孔喉分布，在此基础上优选与渗透率相关性较好的关键参数：Swanson 参数、Win⁃land-r5参数和Pittman 参数（rapex），且为了更全面地表征毛管压力曲线信息，增加代表毛管压力形态的特征参数：歪度、分选系数，结合孔隙度、均值半径，通过留一交叉验证法确定潜变量个数，开展偏最小二乘回归方法分析，建立3 类渗透率预测模型。经数学统计分析对比得到以下结论：①研究区须三段砂岩储层平均孔隙度为2.86%，平均渗透率为0.023 2 mD，整体属于超致密砂岩储层。其孔喉结构复杂、孔渗相关性差，孔喉半径主要为0.01～0.1和0.005～0.01 μm。②经典渗透率预测模型对超致密砂岩储层的适用性较差，Winland 模型等的常规特征孔喉参数r35和r10并不适用，为此提出r5作为特征孔喉参数。不同特征孔喉参数对应的Winland 模型整体表现为由砂岩储层过渡到超致密砂岩储层，特征孔喉半径呈逐渐减小趋势。③Swanson 模型、Pittman 模型、Capillary-Parachor 模型等通过建立毛管压力曲线特征参数与渗透率关系的模型对超致密砂岩储层的适用性仍较差，经分析发现多特征参数存在多重共线性，由此建立的基于普通最小二乘回归方法的渗透率预测模型的应用效果并不理想；且控制渗透率的应为一类孔喉半径的对应区间，采用单一孔喉特征点并不能表征毛管压力曲线的全部信息。因此，该类模型较为适用于渗透率大且孔喉分布较均匀的储层。

超致密砂岩储层渗透率主要受控于孔隙度、孔喉分布、孔喉尺寸等因素，确定多参数最佳潜变量个数为2，基于偏最小二乘回归方法建立的多参数渗透率预测模型：Winland-r5（PLSR）模型、Pittman（PLSR）模型、Swanson（PLSR）模型，对比其拟合效果和均方根误差值，证实拟合效果较好、预测精度高、泛化能力强、工区适用性良好。

符号解释

c1——矩阵X的向量系数；

——矩阵X中第1组成分因子t1的荷载的转置矩阵；

——矩阵X中第r组成分因子tr的荷载的转置矩阵；

d1——矩阵Y的向量系数；

——矩阵Y中第1组成分因子t1的荷载的转置矩阵；

——矩阵Y中第r组成分因子tr的荷载的转置矩阵；

Dm——均值半径，μm；

E1——矩阵X中第1组成分因子的残差矩阵；

Er——矩阵X中第r组成分因子的残差矩阵；

F1——矩阵Y中第1组成分因子的残差矩阵；

Fr——矩阵Y中第r组成分因子的残差矩阵；

G——孔隙几何因子；

i——矩阵X和Y的行数；

j——矩阵X和Y的列数；

K1——Winland-r5模型渗透率预测结果，mD；

K2——Winland-r20模型渗透率预测结果，mD；

K3——Winland-r35模型渗透率预测结果，mD；

K4——Swanson模型渗透率预测结果，mD；

K5——Pittman模型渗透率预测结果，mD；

K6——Capillary-Parachor模型渗透率预测结果，mD；

Kp——歪度；

n——岩心样品的总数，个；

N——样本集容量，个；

p——自变量个数；

pc——毛管压力，MPa；

pcd——排驱压力，MPa；

P——自变量X矩阵容量，个；

Q——因变量X矩阵容量，个；

r——矩阵X和Y的成分因子个数，个；

r5——进汞饱和度为5%时对应的孔喉半径，μm；

r10——进汞饱和度为10%时对应的孔喉半径，μm；

r20——进汞饱和度为20%时对应的孔喉半径，μm；

r35——进汞饱和度为35%时对应的孔喉半径，μm；

ra——最大孔喉半径，μm；

rapex——Pittman 参数，即Swanson 参数对应的孔喉半径，μm；

R2——相关系数；

R2adj——修正相关系数；

RMSE——均方根误差；

SHg——进汞饱和度，%；

SHg∞——理想状态下最大进汞饱和度，%；

Skp——分选系数；

Smax——最大进汞饱和度，%；

t1——矩阵X的第1组成分因子；

tr——矩阵X的第r组成分因子；

u1——矩阵Y的第1组成分因子；

v1——矩阵Y的第1组成分因子u1的权重值；

VIF——方差膨胀因子；

w1——矩阵X的第1组成分因子t1的权重值；

xi——实验测试渗透率，mD；

xij——矩阵X的任意元素；

xP——矩阵X的自变量个数，个；

——矩阵X的第r组主成分因子的标准化变量；

X——自变量矩阵；

Xw1——矩阵X中成分因子相关程度最高变量；

yij——矩阵Y的任意元素；

yk——偏最小二乘回归方程因变量；

yQ——矩阵Y的因变量个数，个；

Y——因变量矩阵；

Yv1——矩阵Y中成分因子相关程度最高变量；

——第1组成分因子最大特征值；

ϕ——孔隙度，%。