高阶煤煤岩毛管压力曲线新数学模型及关键参数

陈 科，唐 磊，尹 超，何 伟，张 伟，权 政

(中海油能源发展股份有限公司工程技术分公司中海油实验中心，天津 300452)

毛管压力曲线对煤层气赋存和开发具有重要意义[1-3]，毛管压力曲线定量化表征对于孔隙结构表征[4]、储层及伤害评价[5-6]、相渗曲线计算[7]具有重要意义。许多专家学者对毛管压力数学模型进行了研究和应用，但对于常规砂岩储层和非常规页岩储层适用的毛管压力数学模型是否也同样适用于高阶煤煤岩，并未达成共识。毛潇潇等[8]、宋播艺等[9]基于分形理论建立了高煤阶煤岩毛管压力分形表征模型，Li Kewen[10]也基于分形几何，建立了能够表征裂缝储层毛管压力的一般性毛管压力模型，然而尹志军等[11]认为由于高阶煤储层具有分段分形特征，目前的毛管压力曲线分形模型不适应于高阶煤；曾建强等[12]对煤岩毛管压力曲线数学模型进行了梳理，结果表明不同的数学模型往往适用于不同物性储层的煤岩毛管压力曲线，认为Li模型能够适应于高煤阶煤岩毛管压力曲线；Liu Pengcheng等[13]基于火柴棍模型建立了一种新的煤岩毛管压力模型，认为该模型比Brooks and Corey模型更适于对煤岩的模拟；袁哲等[14]利用文献[13]建立的新毛管压力模型与实验数据进行了拟合，认为拟合效果较好，但指出采用Matlab软件进行拟合，计算过程相对较为复杂。因此，笔者基于高压压汞数据重新评价了经典毛管压力模型的适应性，提出了新的毛管压力数学模型，并对各参数求解和对毛管压力曲线的影响进行了评价，以期形成适用于高阶煤毛管压力曲线的数学表征模型。

1 实验煤样及方法

1.1 煤样制备

煤样选自某盆地某高阶煤煤层，取样深度500～750 m，将样品加工成直径2.5 cm的柱塞，并放置在105℃恒温箱中烘干至质量不再发生变化。每个柱塞分成两段，一段用于测试煤样基本参数，另一段用于开展高压压汞实验。

1.2 实验方法

煤样渗透率和孔隙率均采用气体测试仪进行，测试气体介质为氦气，测试结果见表1。高压压汞实验采用AutoPore Ⅳ9500型全自动压汞仪开展测试，仪器最大工作压力达到228 MPa，测试孔径范围为0.032～1 000 μm。由于最大工作压力过低导致微孔难以表征，过高则导致煤样孔隙压缩变形，因此，本文设置最大工作压力不超过100 MPa，故本文实验测试的孔径范围为0.075～1 000 μm；实验温度均为室温25℃；由于煤样样品渗透率较低，均小于1×10-3μm2，测定点平衡时间均设定为60 s。依据GB/T 29171—2012《岩石毛管压力曲线的测定》开展高压压汞实验。

表1 实验煤样基本参数Table 1 Basic parameters of the experiment coal sample

1.3 毛管压力曲线

测试得到的煤岩毛管压力曲线如图1所示。图1表明6块煤样毛管压力曲线总体上位于图1左上方，表明煤样物性整体较差，渗透率小于0.31×10-3μm2，孔隙率小于7.1%(表1)；毛管压力曲线基本没有中间平缓段，整体表现为向左上方凸出的形态(图1)，表明孔隙半径分选性差，这与常规砂岩储层及低阶煤储层所具有明显中间平缓段的毛管压力曲线形态完全不一样，主要是由于常规砂岩储层、低阶煤储层以发育孔隙为主，分选性整体较好，相同孔隙半径的孔隙数量和体积较多；而对于高阶煤，微裂缝大量发育，形成裂缝和孔隙双重孔隙介质，孔裂隙半径分选性整体较差，形成了向左上方凸出的曲线形态。

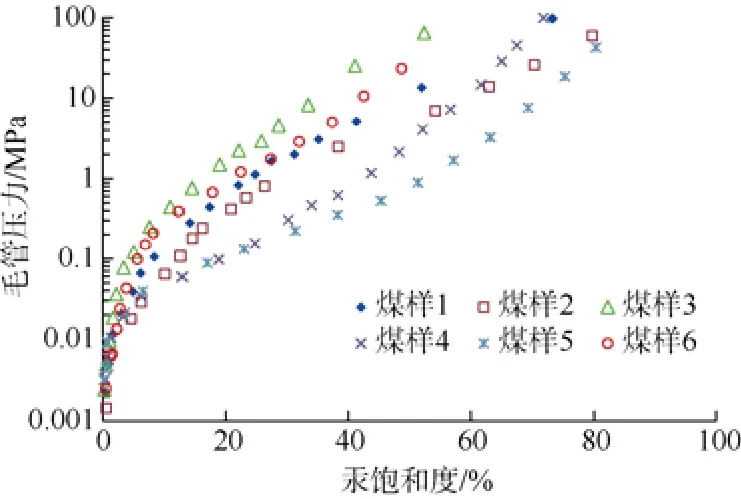
图1 煤样毛管压力曲线Fig.1 Capillary pressure curves of coal samples

2 现有数学模型适应性评价

2.1 Brooks and Corey模型

Brooks and Corey模型(BC模型)是经典的毛管压力拟合模型，能够很好地拟合很多煤样的毛管压力数据，其表达式[15]为：

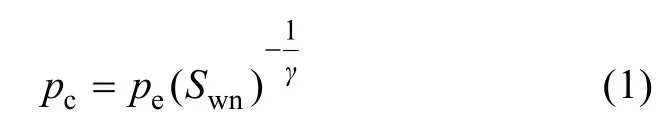
式中：pc为毛管压力，MPa；pe为阀压，即汞开始进入煤样最大孔隙的压力，MPa；Swn为标准化湿相饱和度，小数；γ为孔隙大小分布指数。

处理测试得到的毛管压力数据(图 1)，将数据绘制在以归一化湿相饱和度为横坐标，以毛管压力为纵坐标的双对数坐标中(图 2a)。结果表明，在双对数坐标中，归一化湿相饱和度和毛管压力不呈线性关系，因此不满足式(1)，表明BC模型不能很好地拟合研究区煤样的毛管压力曲线。

图2 现有经典毛管压力模型对研究区煤样毛管压力数据适应性评价Fig.2 Classical mathematical models for capillary pressure and their adaptation for the coal samples in the study area

2.2 贺承祖模型

贺承祖等[16]通过分形定义及压汞参数特征推导出了分形毛管压力模型：

式中：Sw为含水饱和度，%；Df为分形维数，无量纲。

贺承祖模型在常规砂岩储层中使用较为广泛，贾慧敏[17]采用该模型对沁水盆地南部高煤阶煤样分形特征进行了研究，认为煤样具有多段分形特征，即同一煤样具有3个分形维数值，因此，利用式(2)进行毛管压力曲线拟合较为复杂。图2b表明，在湿相饱和度和毛管压力双对数坐标中，6块煤样具有2～3个直线段，证明多段分形特征的存在，同时表明不同煤样的分形区间分界线存在差异，因此，式(2)不适合对毛管压力曲线进行拟合。

2.3 Li模型

Li Kewen[18]通过分形理论推导得到应用更为普遍的毛管压力模型：

式中：SHg为汞饱和度，%。

由式(6)可知，如果毛管压力满足Li模型，则在双对数坐标中，dSHg/dpc与pc呈线性关系，且-1-γ为直线斜率，进而可以方便各个参数的求解。图2c为6块煤样压汞数据根据式(6)处理结果，表明虽然整体上具有一定程度的线性关系，但是相关系数不高，存在离散点较多，因此，Li模型不能很好地拟合研究区煤岩样的毛管压力。袁哲等[14]引进了φ对Li模型进行了改进，但改进后的模型γ和φ的求解非常困难，必须利用公式直接对毛管压力数据进行拟合才能获得各个参数的解，应用起来较为复杂。

3 毛管压力曲线新数学模型

3.1 新数学模型

以毛管压力与最小毛管压力的对数差为横坐标，以进汞饱和度与最小毛管压力的对数差为纵坐标，将图1中毛管压力数据进行处理，结果如图3所示。对图3中数据按最小二乘法进行回归，发现毛管压力与最小毛管压力的对数之差和进汞饱和度与最小毛管压力的对数差满足乘幂关系，斜率为a、幂指数为b(文中直接用a、b表示)，且相关性较好，相关系数均在0.92以上，即可表示为：

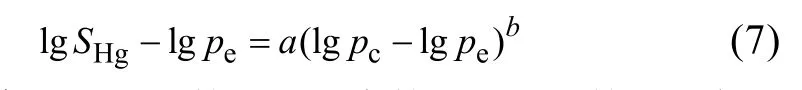
式中：斜率a和幂指数b均为常数，且为正数；pe为汞开始进入煤样孔隙的最小压力，一般为0.001 MPa，则lgpe一般为-3。

整理式(7)可得：

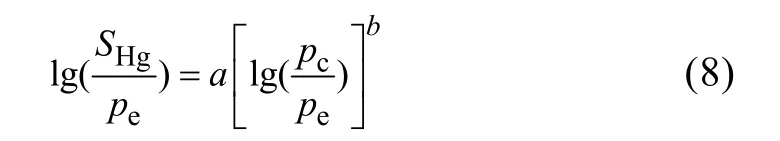
根据式(7)、式(8)，毛管压力曲线计算公式为：

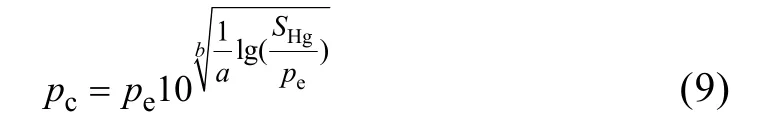
图3 毛管压力和进汞饱和度关系Fig.3 Relationship between the capillary pressure and the mercury saturation

新的煤岩毛管压力数学模型为：

当b=1时，式(8)转化为：

令a=-Fg，则式(10)转变为了Thomeer推导得到的毛管压力和进汞饱和度模型[19]：

式中：Fg为孔隙几何因子。

以上公式表明，Thomeer毛管压力模型为本文毛管压力新数学模型的特殊值，本文提供的毛管压力新数学模型能够适应更多的储层。

3.2 拟合结果

利用式(9)计算得到毛管压力数据，与实验测试得到的毛管压力数据拟合关系如图4所示，由图中可知，二者拟合程度很好，相关性系数均在0.92以上，进一步表明本文提出的数学模型能够很好地拟合研究区煤样的毛管压力曲线。

4 分析与讨论

4.1 斜率a和幂指数b获取方法

将式(8)两边取对数得：

由式(12)可以看出，在双对数坐标中，毛管压力与最小毛管压力的对数差和进汞饱和度与最小毛管压力的对数差呈线性关系，且拟合直线斜率值为b，截距为lga，因此，毛管压力曲线新模型中的2个关键参数均可以通过上述方法进行求取，避免了直接采用式(9)对实验数据进行拟合，使参数求取更加简便快捷，且精确度很高。采用该方法计算得到的6块煤样斜率a、幂指数b值见表1。

4.2 参数对毛管压力的影响

图4 新数学模型和实验数据拟合程度Fig.4 The fitting degree between the new mathematic model and the experiment data

如式(9)所示，为研究斜率a和幂指数b两个关键常数对毛管压力的影响，以煤样1毛管压力曲线为例，根据式(9)模拟斜率a分别为2.5、3.0、3.5和4.0时，其对毛管压力的影响，结果如图5a所示；模拟幂指数b分别为0.10、0.15、0.20、0.25、0.30和0.40时对毛管压力的影响，结果如图5b所示。由图5可知，在其他条件相同时，斜率a和幂指数b均与毛管压力成反比，即当幂指数b为定值且进汞饱和度相同时，斜率a值越小，毛管压力越大；斜率a为定值且进汞饱和度相同时，幂指数b值越小，毛管压力也越大。这表明斜率a和幂指数b能够反映储层物性特征，二者值越大，毛管压力中间平缓段越长、排驱压力越小，则孔隙分选性越好，孔隙中值半径越大，储层物性条件越好；反之，二者值越小，则储层物性条件越差。

图5 新数学模型关键参数对毛管压力影响Fig.5 Effect of the key parameters of the new mathematic model on the capillary pressure

5 结论

a.高阶煤岩毛管压力曲线总体上位于左上方，基本没有中间平缓段，整体表现为向左上方凸出的形态，与常规砂岩、低阶煤岩毛管压力曲线形态完全不一样。BC模型、贺承祖模型和Li模型均不能很好地拟合高阶煤岩的毛管压力曲线。

c.在双对数坐标中，毛管压力和最小毛管压力的对数差与进汞饱和度与最小毛管压力的对数差呈线性关系，可利用该线性关系直接求取毛管压力模型的斜率a和幂指数b。在其他条件相同时，斜率a和幂指数b均与毛管压力成反比。