概率神经网络在盐水水淹层识别中的应用

李 健，杨明任，杜玉山，申辉林，刘 丽，孙启鹏

（1.中国石化胜利油田分公司勘探开发研究院，山东东营 257015；2.中国石油大学（华东）地球科学与技术学院，山东青岛 266580）

近年来，中国各油田经过长期的注水开发已经进入中后期阶段，复杂的地质条件及过高的注水开发比例导致水淹问题日益严峻。由于油田的地质特征、水驱开发及资源条件不同，尚未有一套通用且有效的水淹层测井识别方法［1］。用于水淹层识别的自然电位基线偏移法、径向电阻率对比法、传统的交会图技术等受到仪器精度、测井环境等因素的影响效果不佳［2］，同时水淹机理研究不透彻，测井响应特征复杂多变，多解性较强。对于核磁共振测井等方法虽然对水淹层识别精度较高，但成本过高未能广泛应用。

近年来机器学习方法快速发展，在科学和工程领域应用广泛并获得突破性的成果，为提高水淹层的识别精度提供了新的思路和方法。诸多专家对此进行了深入研究，已将常规的机器学习方法应用于水淹层识别，如支持向量机（SVM）［3-4］、模糊逻辑模型（FLM）［5-6］等算法，在一定条件下取得了较好的预测效果。马陇飞等利用决策树方法有效解决了交会图版法存在的多解性问题，且能快速高效地处理大量数据并自动分类［7-10］。王振伟对碳酸盐岩储层进行了分类，针对不同储层类型分别建立了水淹层测井评价方法，取得了较好效果［11］，但也存在决策树算法在分类较多时精度会下降，支持向量机算法无法训练大规模样本，难以解决多分类等相关问题。由HINTON 等提出的深度学习方法是当前机器学习领域最热门的方向之一，其网络结构复杂且具有多个隐含层，不仅能通过提取每层特征将样本的原始空间特征转换成新的高维空间特征来表示，还能为数据建立更加抽象的特征描述，从而将回归预测或分类问题简单化且提高准确性［12-14］。概率神经网络（PNN）作为深度学习的研究热点之一，其实质是基于贝叶斯最小风险准则发展而来的一种并行算法，同时不像传统的多层前向网络需要用BP算法进行反向误差传播的计算，而是完全前向的计算，其训练时间短、不易产生局部最优，且分类正确率较高，可保证获得贝叶斯准则下的最优解。相比之下，Adaboost 算法作为当前深度学习分类效果较好的网络模型之一，具有分类速度快，可应用多个弱分类器经过线性组合成强分类器。

胜利油区埕岛油田注入水主要是以海水、污水混注为主，水淹类型主要是盐水水淹，地层电阻率随水淹程度增强呈单调递减的特征，但地层电阻率递减量与水淹程度关系极其复杂，至今无有效识别水淹层及其水淹程度的方法。为此，笔者提出一种基于概率神经网络的盐水水淹层识别方法，并利用Adaboost 算法进行对比分析，在分析测井特征参数与水淹程度相关性基础上，选取井径（CAL）、自然电位（SP）、密度（DEN）、深侧向电阻率（Rt）和浅侧向电阻率（RS）等5条敏感曲线的平均值作为输入参数来预测靶区的水淹级别，预测结果表明，利用深度学习方法中的概率神经网络算法能有效提高盐水水淹层识别精度。

1 方法原理

1.1 Adaboost算法

FREUND 等在1999 年提出Boosting 算法［15］，该算法在Probably Approximately Correct 学习问题框架模型下能提高任意给定弱分类器分类精度，为了解决实际应用中的问题，在2003 年又提出了Adaboost（自适应增强）算法［16］，该算法是一种迭代算法，其预测准确、分类快、几乎不出现过拟合现象，核心是对每个训练样本赋予相同的初始权重，每一轮弱分类器训练过后均会根据其表现对每个错误分类样本的权重作出相应调整，增加错误分类样本的权重，这样之前出错的训练样本在下一轮学习训练中即可得到更多关注，按这样的迭代过程重复训练出M个弱分类器，最后进行线性加权组合成一个强分类器［17］（图1）。

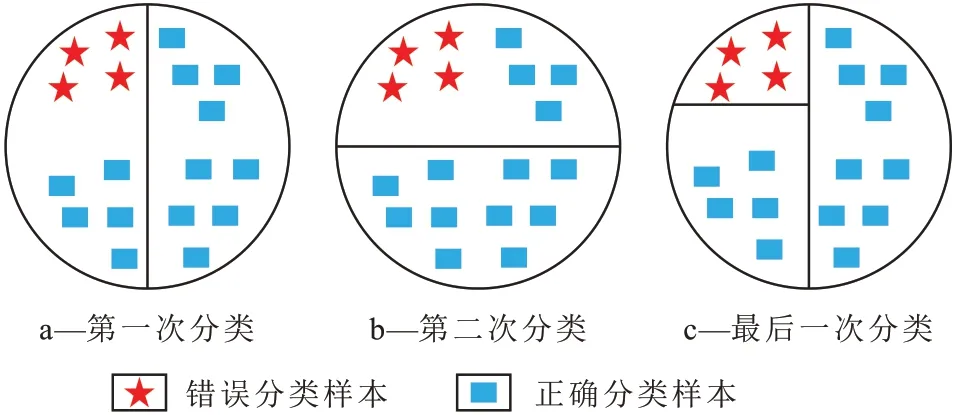
图1 Adaboost算法原理示意Fig.1 Principle of Adaboost algorithm

输入过程 假设给定一个二类分类的训练样本为：

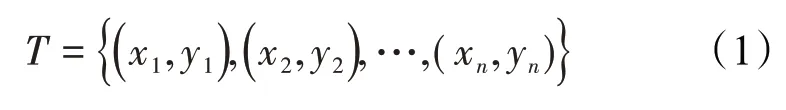
其中，每个样本点由实例和标记组成。实例为xi∈X∈Rn，标记为yi∈Y∈{-1，1}，弱分类器为Gm（x）。

输出过程 假设给定一个强分类器为G（x）。

①训练样本上的权值分布为：

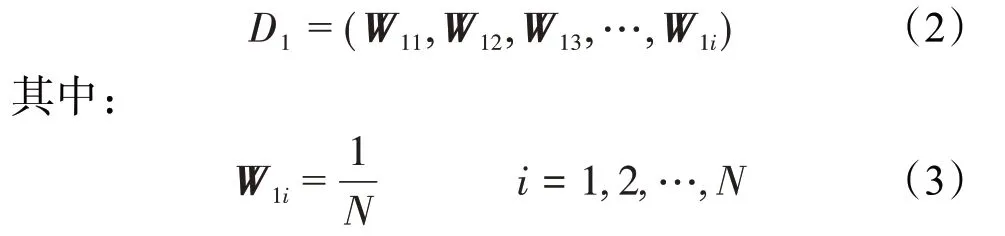
②训练样本各项参数的计算与更新

将具有权值分布Dm的训练样本用于学习训练，得到弱分类器表达式为：

计算弱分类器分类目标为最小化在权值分布下训练样本的分类误差率：

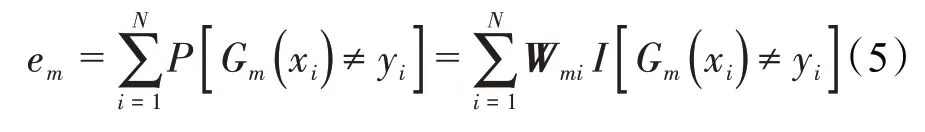
弱分类器系数的计算公式为：

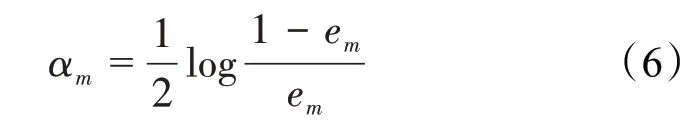
新的训练样本权值分布的计算公式为：

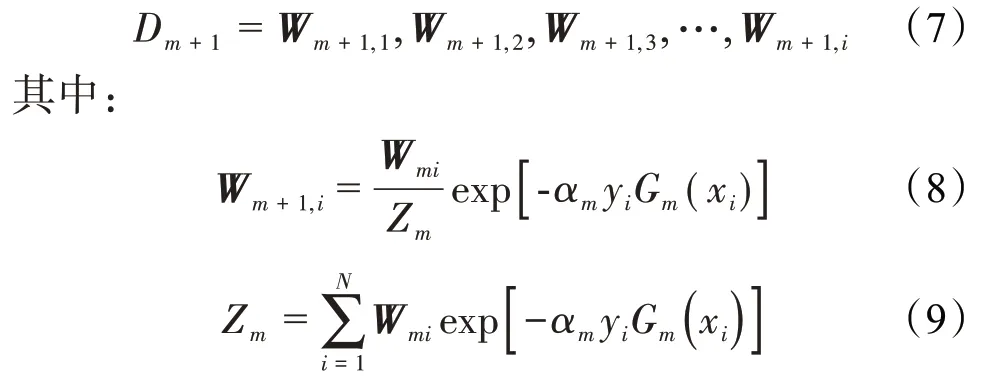
③建立弱分类器的线性组合方程式为：

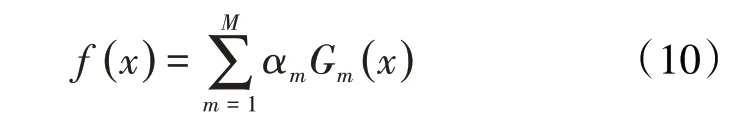
由（1）—（10）式得到的强分类器表达式为：

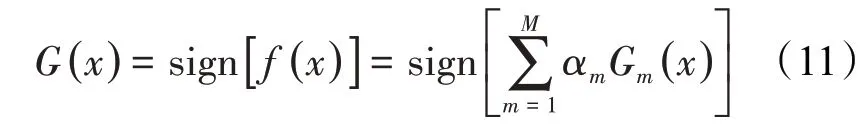
1.2 概率神经网络

概率神经网络（Probabilistic Neural Network，简称PNN）最早于1990 年由数学家SPECHT［18］提出。PNN 是一种基于概率密度函数且泛化能力很强的神经网络，结合了径向基函数和概率密度函数的优点，具有结构简单、复杂度低等特性，多用于模式分类，也可用于插值［19］。概率神经网络由输入层、模式层、求和层、输出层等组成（图2）。

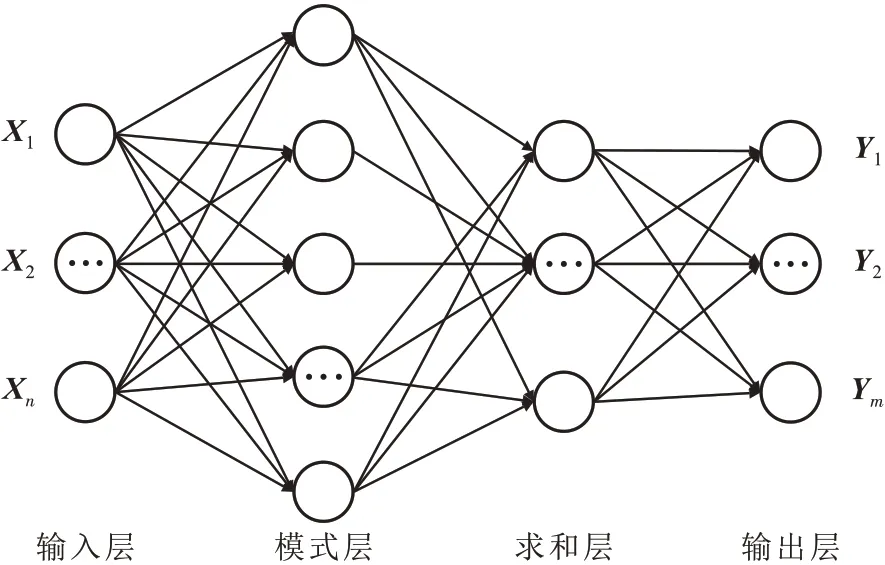
图2 概率神经网络结构Fig.2 Structure of probabilistic neural network

输入层 输入层的每个神经元均为单输入、单输出，将输入单元X用分布的方式表示并传递给模式层的所有神经元，其传递函数是线性的。其中X=［X1，X2，…，Xn］。

模式层 模式层与输入层之间通过权重Wij连接，该层第j个神经元的实际输入为：

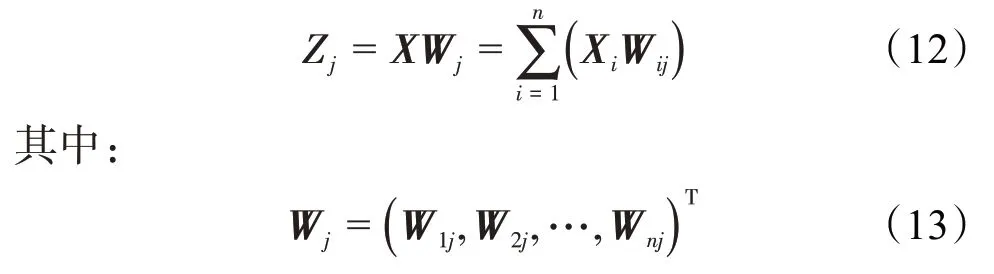
模式层的传递函数用径向基函数表示，其表达式为：

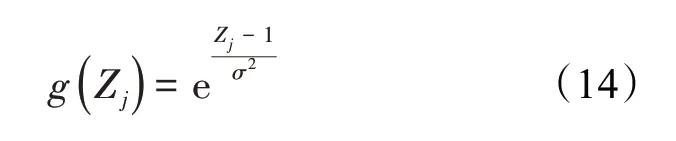
这是PNN 与全连接神经网络的不同之处，若X和Wij均为统一量纲的单位长度，则（14）式相当于：

由于模式层采用的是径向基非线性函数映射，可避免反向传播神经网络的局部最小值问题［20］。

求和层 求和层具有线性求和功能，有选择地对模式层的输出进行求和，计算属于未水淹、弱水淹、中水淹、强水淹和特强水淹的概率，计算公式为：

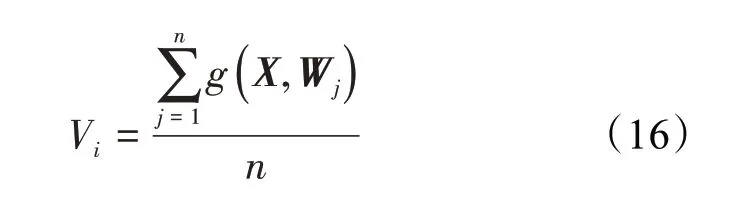
输出层 该层具有判决功能，取求和层中最大的一个作为输出的类别，计算公式为：

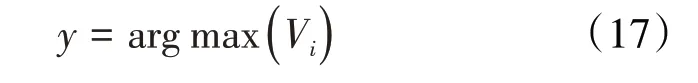
根据上述理论研制开发了概率神经网络预测水淹层处理软件，为水淹层测井PNN 自动识别奠定了理论基础。

2 运用概率神经网络进行水淹层识别

2.1 测井特征参数优选

对埕岛油田盐水水淹层进行测井曲线响应特征分析发现，每1 条测井曲线对水淹层均有或多或少的响应特征，但是因为每种测井方法均是基于一种物理原理基础上提取的地球物理测井信息，所以测井曲线均不可避免地存在较严重的多解性。为此，根据埕岛油田实际测井资料和生产测试结论进行测井特征参数与水淹层产水率的相关性分析。由于每条测井曲线在不同水淹级别的测井响应特征不同，应用偏最小二乘法进行所有测井特征参数与产水率的相关性分析（图3）可以看出，水淹层测井特征参数相关性频率为正值，则表明提取的特征参数与产水率呈正相关，否则呈负相关，且水淹层测井特征参数相关性频率的绝对值越大表明提取的特征参数与产水率相关性越好；自然电位、密度、浅侧向电阻率与产水率的正相关性最好，而井径、深侧向电阻率与产水率的负相关性最好。由此择优选取上述最能有效反映埕岛油田盐水水淹层测井响应特征的5个特征参数对靶区盐水水淹层进行识别。

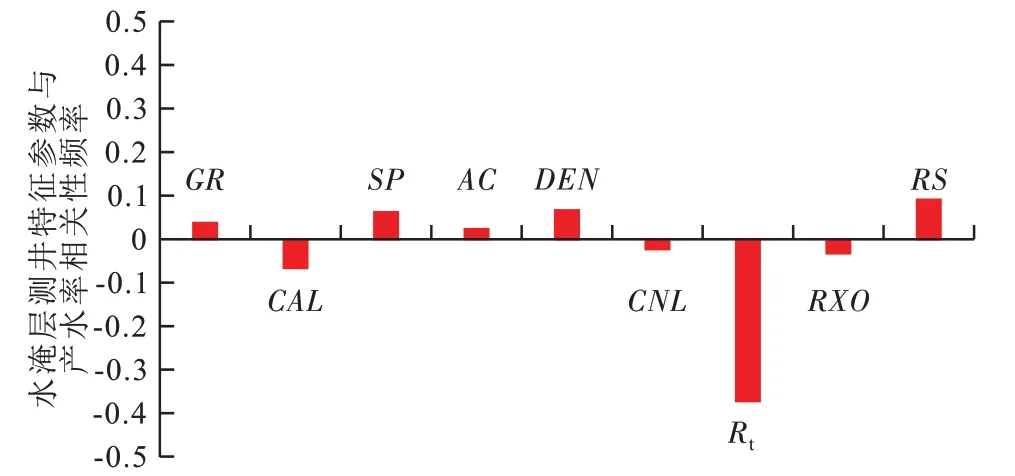
图3 测井特征参数与产水率相关性频率直方图Fig.3 Correlation frequency between logging characteristic parameters and water cut

2.2 测井曲线归一化处理

测井曲线归一化处理将确保各测井参数处于规范的分布范围内，使网络模型更易学习到各参数之间的关联性。由于各曲线数据量纲不一致，在进入概率神经网络和Adaboost算法之前训练样本和测试样本必须进行归一化处理，将其刻度在统一的数值量纲范围内。对于近似线性特征的输入数据，可采用线性归一化公式为：

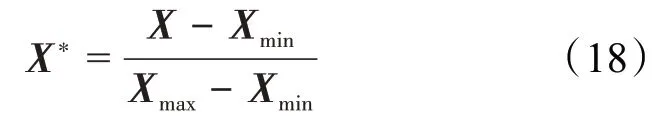
而对于电阻率曲线等非线性对数特征的曲线，可采用对数归一化公式为：

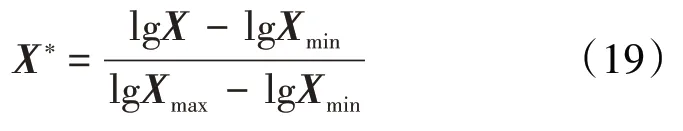
2.3 PNN模型训练

按照埕岛油田盐水水淹级别标准划分的5个水淹级别（表1），选取靶区具有代表性的实际测井数据作为训练样本数组，具体选取了63个样本数据作为训练样本，以未水淹、弱水淹、中水淹、强水淹和特强水淹等5个水淹级别作为期望输出向量。在训练过程中将井径、自然电位、密度、深侧向电阻率和浅侧向电阻率等5条敏感测井曲线的均值作为输入参数输入到概率神经网络和Adaboost算法中进行水淹层识别，PNN 网络模型的权值是迭代更新的，不断优化平滑因子是训练网络模型的核心，尽可能降低训练样本的误差，并使用多层感知器优化。训练时使用求和层神经元返回的所有训练样本的所有值来评价不同组平滑因子的误差标准［21］。在神经网络结构方面，建立一个输入层节点数为5、模式层节点数为15、求和层节点数为10、输出层节点数为5的概率神经网络拓扑结构，训练网络从而得到水淹层识别的PNN 网络模型［22］。Adaboost 算法也采用相同的模型参数和算法结构以保证训练与预测结果的可靠性与可对比性。

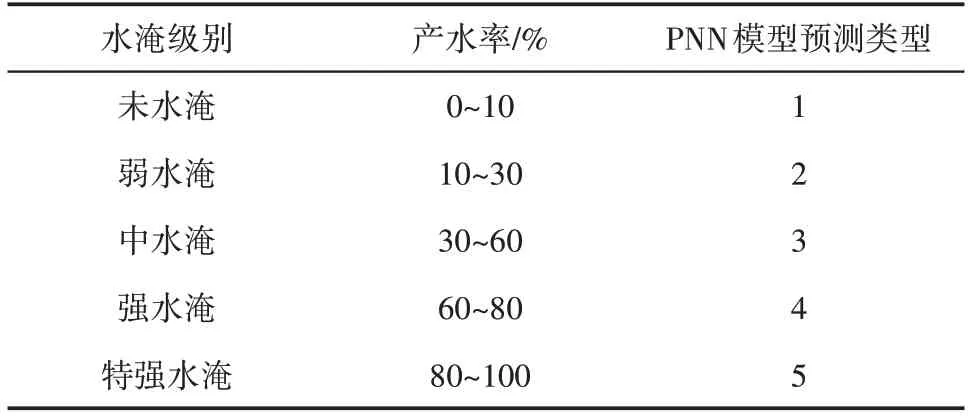
表1 埕岛油田盐水水淹层划分标准Table1 Classification standard of saline water flooded layers in Chengdao Oilfield

在网络训练完成后进行网络性能测试，将每层神经元间的连接权重代回到网络中，重新对训练样本进行水淹层预测。从表2 中可以看出，训练样本的水淹级别与概率神经网络的预测结果完全相同，证明完善的概率神经网络和Adaboost算法已训练完成，可以用于测试样本的水淹层识别［23］。

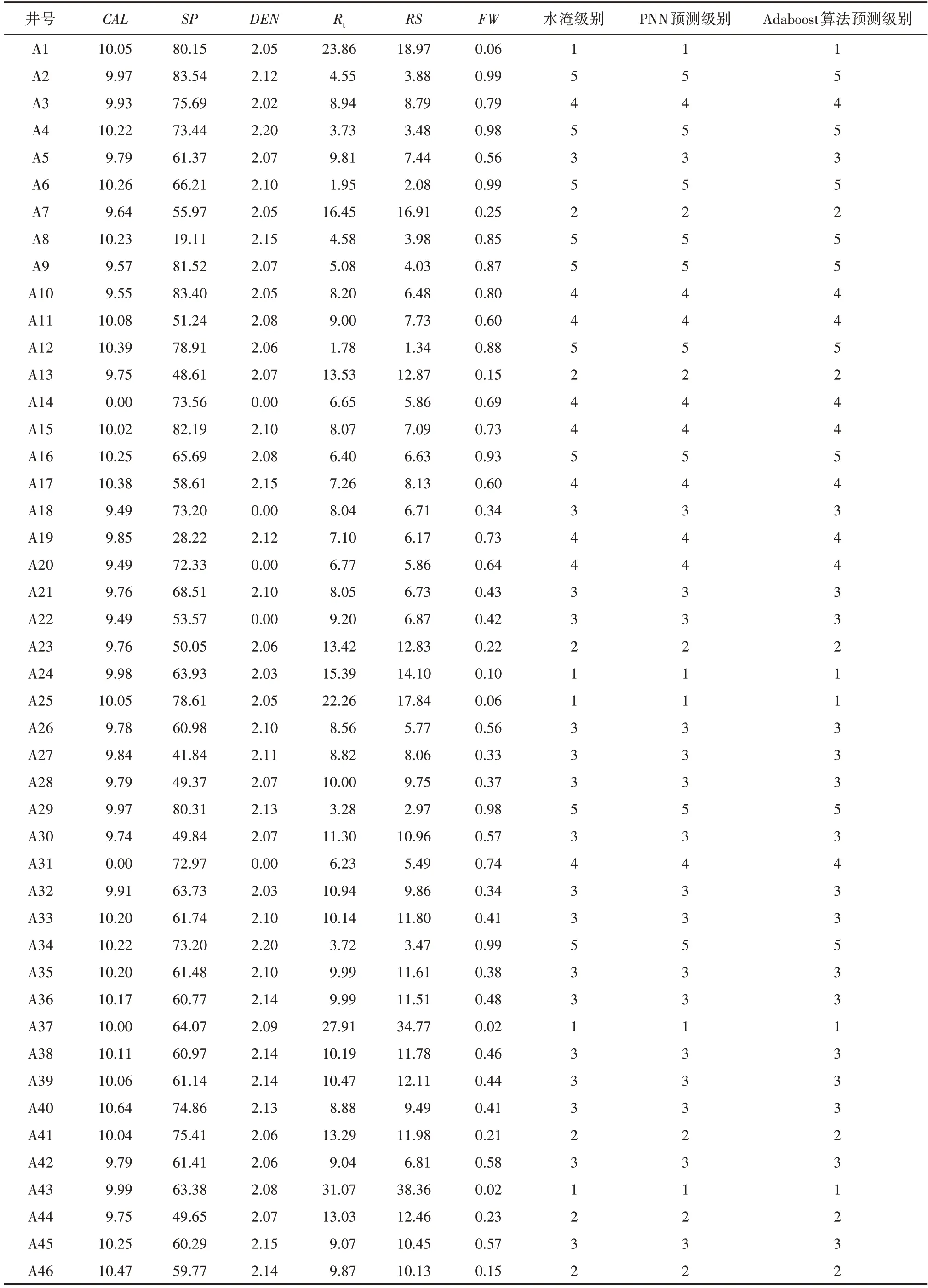
表2 训练样本的概率神经网络和Adaboost算法水淹层识别结果Table2 Flooded layer identification by probabilistic neural network and Adaboost algorithm of training samples

2.4 概率神经网络预测水淹层及其效果分析

通过对网络模型泛化后，将训练成功的概率神经网络和Adaboost 算法用于识别盐水水淹层。为此，在靶区随机选取30个测试样本进行水淹层实际预测（表3，表4）。从预测结果发现，PNN 模型在靶区水淹级别样本分类正确的有27个样本，预测准确率达到90%；Adaboost 算法在靶区水淹级别样本分类正确的有24 个样本，预测准确率达到80%；PNN模型的水淹层识别精度提高了10%，错误分类样本都集中在中水淹、强水淹和特强水淹级别，并且预测误差没有出现水淹级别跨级别的现象，取得了理想效果。在水淹层测井PNN 模型预测时，若能选取更具有区域代表性的学习样本，则将取得更好的水淹层测井识别效果［24］。

表3 测试样本的概率神经网络和Adaboost算法水淹层识别结果Table3 Flooded layer identification by probabilistic neural network and Adaboost algorithm of testing samples

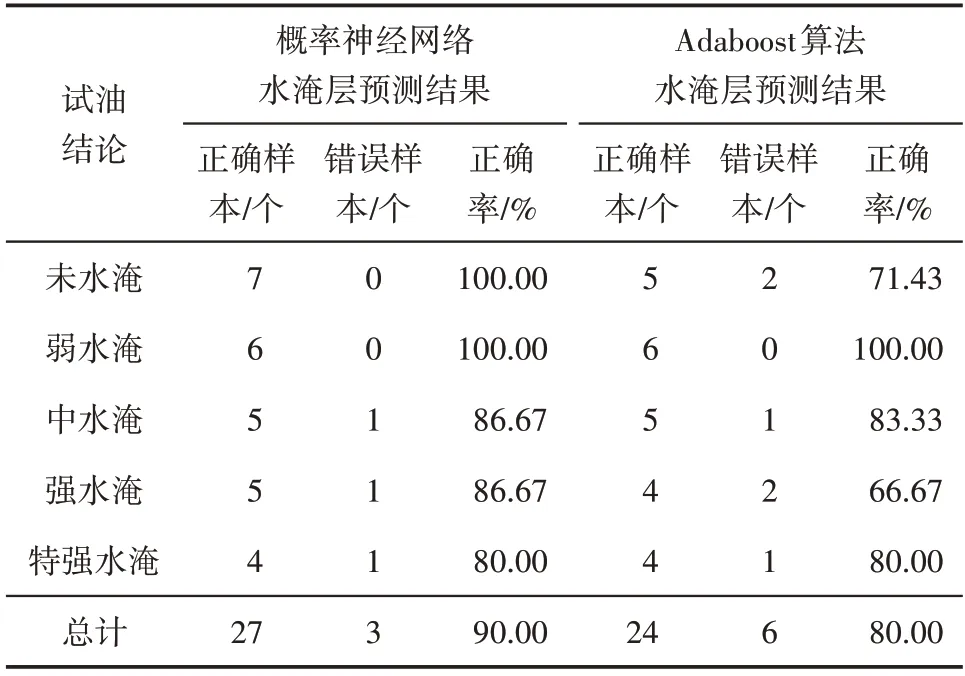
表4 概率神经网络与Adaboost算法水淹层预测结果与试油结论对比分析Table4 Comparison analysis of flooded layer prediction results from probabilistic neural network and Adaboost algorithm with test results

3 实例应用

从靶区A85 井水淹层测井解释成果（图4）可以看出，测试井段为1 916.0～1 923.5 m，日产油量为15.2 t/d，日产液量为17.2 t/d，综合含水率为11.63%，自然伽马曲线显示低值且有明显的正韵律沉积特征，自然电位曲线呈正异常和微弱的基线偏移现象，声波时差值呈局部极大，深浅侧向电阻率底部呈低值且有显著的泥浆低侵特征，呈现典型的弱水淹层特征。依据变倍数物质平衡法定量计算的产水率平均为19.15%，测井定量解释结论为弱水淹层，而应用PNN 模型和Adaboost 算法对A85 井测试井段预测水淹级别均为2，即为弱水淹层，与定量解释和生产测试结论完全一致。

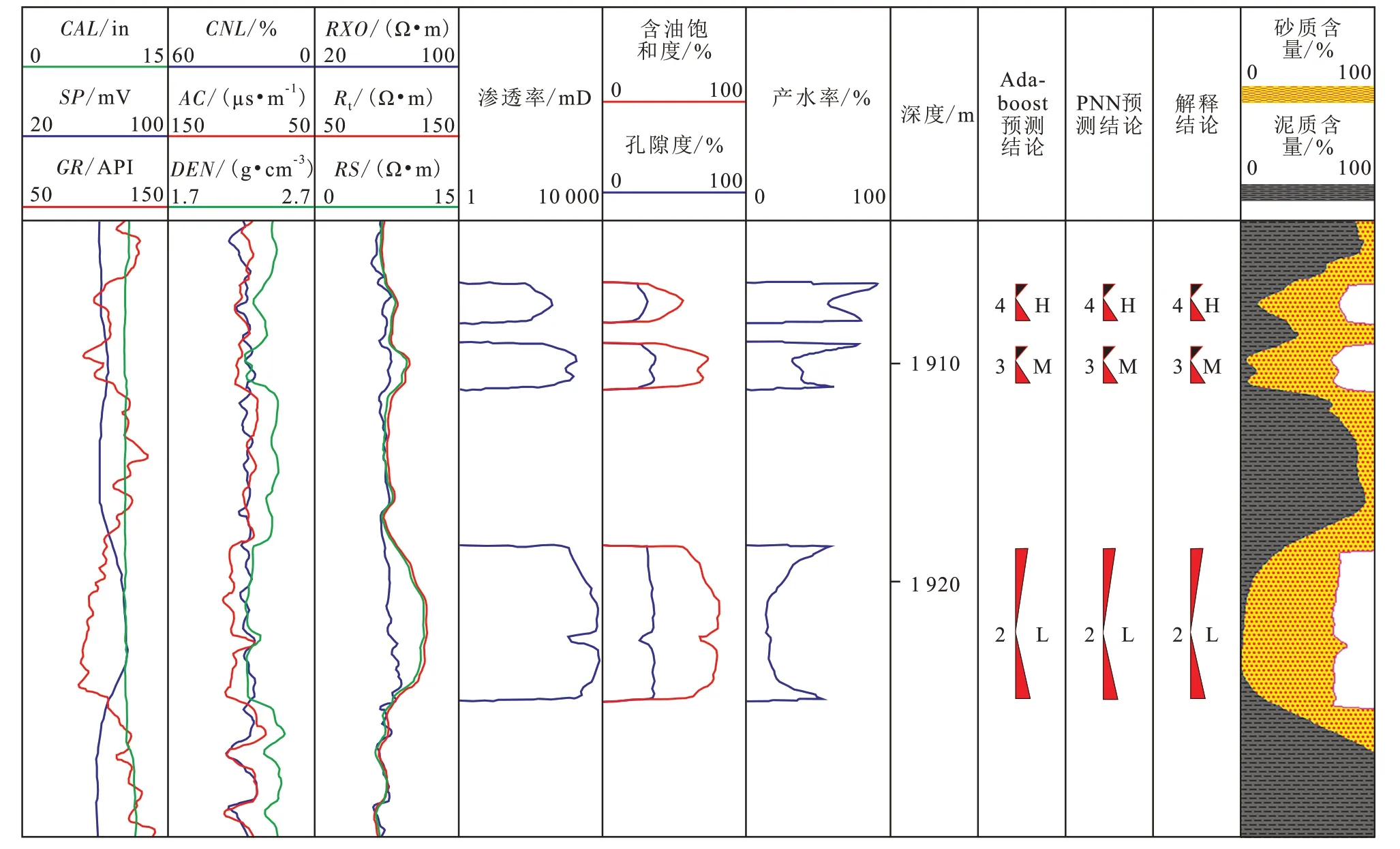
图4 埕岛油田A85井盐水水淹层测井预测及定量解释成果Fig.4 Well logging prediction and quantitative interpretation of saline water flooded layers in Well A85 of Chengdao Oilfield

综上所述，概率神经网络PNN 模型在埕岛油田盐水水淹层识别中具有适用性强、应用方便、易于实现、精确度高等特点。

4 结论

盐水水淹层电阻率随水淹程度增强呈现单调递减的特征，但地层电阻率递减量与水淹程度关系极其复杂，是盐水水淹层定量评价的关键，至今还没有有效识别水淹层及其水淹程度的方法。为此提出的概率神经网络与当前深度学习分类效果较好的Adaboost 算法和其他机器学习的分类模型相比，具有训练速度快、结构简单、分类精度高等特点，便于实现和推广应用。结合测井特征参数和测试结论对判识样本进行水淹层预测，结果表明深度学习方法中的概率神经网络的水淹层预测精度提升了10%，可以有效地提高盐水水淹层识别精度，为研究区块水淹层评价提供参考和借鉴；概率神经网络不仅可以应用到水淹层识别上，还可以应用在岩性、裂缝、产能等不同储层特征参数的预测上，具有较高的理论参考和推广应用价值。

符号解释

D1——权值集合；

Dm+1——权值分布；

Dm——权值集合；

em——分类误差率；

f（x）——线性函数；

g——径向基函数；

g（X，Wj）——模式层的输出；

G（x）——强分类器；

Gm（x）——弱分类器；

Gm（xi）——第i个弱分类器；

i——序号；

I——分类错误的样本；

j——模式层神经元个数；

m，M——弱分类器个数；

n——第i类的神经元个数；

N——样本个数；

P——分类错误的样本概率；

Rn——实数；

T——测井数据的训练样本；

Vi——第i类别的输出；

W——权值矩阵；

W1i——第i个样本点的权值；

Wj，Wij——模式层与输入层之间的权值；

Wmi，Wni——每个样本的权值；

Wm+1，i——第i个训练样本的权值；

Wnj——第n个标记点第j个神经元的权值；

x——向量集合；

xi——第i个实物样本；

xn——第n个向量；

Xn——第n个实例样本；

Xi——实例样本，i=1，2，…，n；

X——输入矩阵，样本集合（测井数据）；

X*——经过归一化后的测井数据；

Xmax——测井曲线的最大值；

Xmin——测井曲线的最小值；

y——输出层中的输出，即为最终预测结果；

yn——第n个标记样本；

yi——标记样本，i=1，2，…，n；

Y——输出矩阵，标记集合；

Ym——预测数据值；

Zm——规范化因子；

Zj——模式层第j个神经元和实际输入值；

αm——弱分类器的系数；

σ——平滑参数。