多回路PID控制下的两轮平衡车系统设计
刘泽伟,冯靖靖,李婉钰,赵 倩
(1.曲阜师范大学工学院,山东 日照 276826;2.曲阜师范大学计算机学院,山东 日照 276826)
0 引言
移动机器人因集控制、计算机、电子、机械等多学科知识于一体,已成为目前科学研究较活跃的领域之一。同时,随着移动机器人的智能化发展[1],其应用范围越来越广泛,面临的环境和任务也越来越复杂。两轮平衡车的概念正是在这一背景下被提出来的。两轮平衡车自身的不稳定性以及非线性使它成为优良的验证控制理论和控制方法的平台。
针对两轮自平衡机器人,目前采用的控制策略主要有传统比例积分微分(proportional integral differential,PID)控制、模糊比例微分(fuzzy proportional-differential,FuzzyPD)控制等[2]。其中,传统PID控制相较于其他控制算法[3],不需要建立准确的数学模型和专家经验,控制面广泛且易于实现,但仍存在易受干扰、高速下稳定性和响应性差的问题。为解决该问题,本系统从控制器结构入手,设计了以角速度环为主回路的双串级PID控制器。该控制器采用LPC54606为主控芯片,并以搭配姿态、图像、速度等多个传感器的两轮平衡车作为被控对象。经实测,车速提升后的系统稳定性和响应速度良好。
1 硬件系统设计
硬件系统如图1所示。系统硬件主要由LPC54606单片机、互补金属氧化物(complementary metal oxide semiconductor,CMOS)摄像头、六轴惯性测量单元(inertial measurement unit,IMU)、1 024线编码器、主从一体式蓝牙、电机驱动组成。摄像头、陀螺仪和编码器的数据作为单片机的输入。电机驱动作为单片机的输出。LPC54606单片机主要完成姿态、速度、方向三个模块的数据处理以及控制器算法实现。蓝牙仅在PID参数整定、试验数据采集时开启,在正常循迹时关闭。所有模块由所设计的升压、稳压、降压电源电路提供电力。

图1 硬件系统框图
2 姿态信息采集及处理
目前的两轮平衡车姿态数据测量大多通过陀螺仪和加速度计等IMU模块获取。陀螺仪具有较好的动态性能,但用角速度积分得到角度的检测方法会累加漂移误差。加速度计静态特性好,但运动过程中产生的运动加速度会干扰输出信号。故需要利用滤波器算法融合两者各自得到的角度信息,从而最大程度地抑制噪声对测量角度的影响。
2.1 原始数据处理及单位转换
利用单片机模拟集成电路总线(inter-integrated circuit,I2C)与IMU模块通信,所读取到的IMU多字节数据为加速度计和陀螺仪的原始数据,经过数据处理和单位转换后的数据才可用于后续处理。
(1)
式中:G0和G分别为IMU单位转换前后的角速度,rad/s;D为陀螺仪角速度零点偏差;K1为陀螺灵敏度。
(2)
式中:A0和A分别为IMU单位转换前后的加速度;K2为三轴加速度计灵敏度,m/s2。
对单片机进行多次在线调试,确定上电后,D长时间内在一微小数值范围内变化,对于本系统可设置为定值。配置IMU三轴陀螺仪寄存器的FS_SEL=3,则量程范围为±34.9 rad/s,选定16位带符号数作为测量数据输出,最大值为±32 767,故K1=938.9 LSB/(rad/s)。同理可求,K2=16 384 LSB/g(g为重力加速度)。
2.2 卡尔曼滤波下的数据融合
两轮平衡车这一自然不稳定系统需具有快速响应以及高适应性的特点,从而在复杂环境下保持自我动态平衡。故本系统选择适应于动态环境下且具有较高融合精度的卡尔曼滤波算法。卡尔曼滤波是一种从含噪声的测量值中估计系统状态的、应用于离散线性滤波的迭代算法,具有较强抑制噪声的能力,在航天技术、通信工程等领域有着广泛应用[4-5]。
卡尔曼滤波器算法实现过程如下[6]。
①二维状态向量系统的构建。
研究两轮平衡车的直立状态,即为研究车体的俯仰状态。由于俯仰角和俯仰角速度为导数关系,本系统将车体实际俯仰角θ作为一个状态向量。系统俯仰角选取绕x轴,偏航角选取绕y轴,横滚角选取绕z轴,计算式如式(3)所示。
(3)
式中:Ay和Az分别为加速度计y轴和z轴重力加速度[7]。
以加速度计估计得到的陀螺仪常值偏差b作为另一状态向量。构建二维状态向量系统,故卡尔曼滤波器中向量均为二维向量,便于在单片机中编程实现。
②用离散化方程描述连续系统。
状态预测方程为:
X(k)=AX(k-1)+BU(k-1)+W(k-1)
(4)

观测方程为:
Z(k)=H(k)X(k)+V(k)
(5)
式中:Z(k)为加速度计测得的角度;H为(k-1)时刻到k时刻的状态变量对观测量增益矩阵;V(k)为k时刻加速度计观测噪声。
③预测阶段。
要估计k时刻的实际角度,必须根据(k-1)时刻的角度来预测,同时计算k时刻的系统噪声协方差。
先验估计计算式为:
X(kk-1)=AX(k-1k-1)AT+BU(k)
(6)
式中:X(kk-1)为利用(k-1)时刻的角度预测出的角度结果;X(k-1k-1)为(k-1)时刻的最优角度。
计算误差协方差:
P(kk-1)=AP(k-1k-1)+Q
(7)
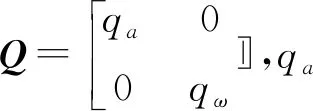
qa和qω数值代表卡尔曼滤波器对于所用IMU模块数据的信任程度,值越小代表信任程度越高,则系统中陀螺仪值更接近于实际值。因此,qω小于qa,一般小三个数量级左右。
④校正阶段。
卡尔曼增益计算式为:
(8)
式中:Kg(k)为卡尔曼增益;H为系数矩阵,由于陀螺仪积分得到的角度值与加速度计测得角度值相对应,故H=[1 0];R为测量噪声的协方差矩阵,R=[Rθ],Rθ越大则观测值中被卡尔曼滤波器视为噪声的成分越大。
后验估计计算式为:
X(kk)=X(kk-1)+Kg(k)Z(k)-HX(kk-1)
(9)
更新误差协方差:
P(kk)=[I-Kg(k)H]P(kk-1)
(10)
式中:I为单位矩阵。
⑤迭代计算。
在已得到k时刻的角度最优估计值的前提下,当系统进入(k+1)时刻状态,k时刻的后验估计将作为(k+1)时刻的先验估计。重复预测阶段和校正阶段,使卡尔曼滤波器循环下去,得到姿态的最优估计。
2.3 卡尔曼滤波算法参数调试
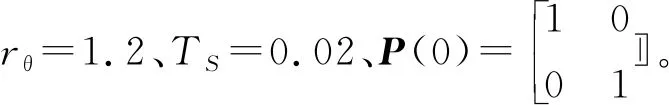
3 多回路PID控制及分析
本系统采用以角速度环为主回路的双串级PID来改善传统PID控制结构,即串级转向环和串级直立行驶环。该串级控制理论衍生于四轴飞行器[8-9]。多回路PID控制结构如图2所示。
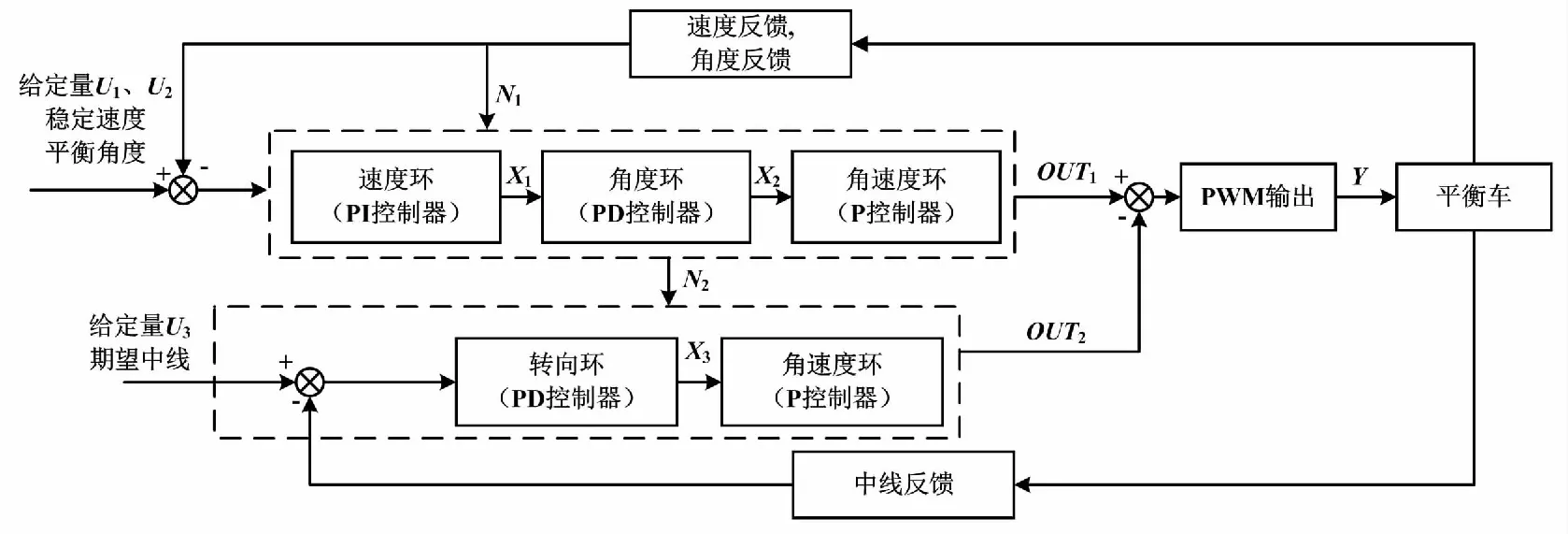
图2 多回路PID控制结构图
图2中:X1为速度环输出;X2为角度环输出;X3为转向环输出;N1为直立闭环控制器受到的干扰信号;N2为方向闭环控制器受到的干扰信号;OUT1为直立闭环控制器的输出;OUT2为方向闭环控制器的输出。
两个角速度环的输出不同。直立速度控制的角速度环输出为两电机的脉宽调制(pulse width modulation,PWM)波信号。串级转向的角速度环输出为两电机差速转弯时的PWM差值。两者叠加在电机上,如式(11)所示。
PL,R=Pθ±PT
(11)
式中:PL,R为左右两电机的PWM值;Pθ为直立速度环输出的PWM值;PT为串级转向环输出的两电机差速转弯时的PWM差值。
3.1 串级直立行驶闭环控制
①角速度环。
角速度环的存在减少了直立车的震荡。通过比较现有角速度与理想目标角速度,使直立车可以快速达到目标速度,输出PWM控制电机,使车体保持角速度为0。在确保角速度调整的快速响应下,PID控制中微分D的影响最小,可以忽略。积分I起主要作用,可以有效地消除稳态温差,但过大的积分量会破坏系统平衡,使参数难调试且易超调。故本系统只取比例P来进行控制,在一定程度上减少了扰动和干扰,有利于系统的稳定。位置式角速度环比例积分(proportional integral,PI)控制的关键代码如下。
Gyro_Error=Angle_Output-fgyrox;//与角度环串联
Gyro_Output=Gyro_Kp * Gyro_Error;//P控制
Gyro_Output=limit(Gyro_Output,1000,-1000);//输出限幅
代码中,角速度环的输入为期望角速度和俯仰轴角速度,对应于代码中的Angle_Output 和fgyrox。在离散化采样处理中,Gyro_Error为当前时刻的角速度偏差。输出限幅则是为了滤除高频干扰,防止输出值过大。
②角度环。
角速度环只能使车勉强立住,而使车在机械零位保持角速度为0是直立的关键,故串入角度环使直立车固定在设定角度。通过比较现有角度和目标角度,输出此时理想的角速度。在确保角度不会过大产生震荡的情况下,可以只利用比例P来控制,出现轻微震荡再加入微分D,最终系统选定比例微分(proportional differentral,PD)控制器来控制。位置式角度环PD控制的关键代码如下。
Angle_Error=(Set_Point +Speed_Output)-angle;//与速度环串联
Angle_Sum_Error +=Angle_Error;//累加误差
Angle_Output=Angle_Kp * Angle_Error +Angle_Kd * fgyrox;//PD控制
代码中,角度环的输入为期望角度值和俯仰轴角速度。前者为机械零位Set_Point和速度环输出的偏差量Speed_Output的和。后者为fgyrox。angle为实际角度。在离散化采样处理中,Angle_Error为当前时刻角度偏差。
③速度环。
前两个环只能让车稳稳地立在原地,但不能维持车速,一旦加速或减速便会打破直立平衡。故本设计在串级直立控制的基础上串入速度控制。速度环的存在使车以一定速度前进,将现有速度与设定速度比较,输出直立车行驶应保持的角度。控制器只需加入比例P便可实现优良的速度控制,而积分I可以让速度更稳定。故本系统选择引入PI控制器。增量式速度环PI控制的关键代码如下。
Speed_Error=(Set_Speed-Real_Speed)-(angle-Set_Point);//与角度建立联系
Speed_OutNew+=Speed_Kp * (Last_Speed-Real_Speed)+Speed_Ki * Speed_Error;//PI控制
Speed_OutNew=SpeedOutOld * 0.6 +SpeedOutNew * 0.4;//一阶低通滤波
代码中,速度环的输入为期望速度和实际速度,即代码中的Set_Speed和Real_Speed。Speed_Error为当前时刻的速度偏差。一阶低通滤波可防止速度发生突变[10]。
3.2 串级方向闭环控制
转向内环是为了消除两电机机芯的偏差,使平衡车上电放置后沿直线行驶,系统选定P控制。转向外环则是建立与图像传感器之间的控制联系,其存在是使平衡车能够按所计算的实际中线循迹。但若只靠单纯的比例控制,偏离中线方向多就转得多,很容易造成抖动和过冲。故本文在比例P控制的基础上引入图像权重法。位置式转向外环P控制的核心代码如下。
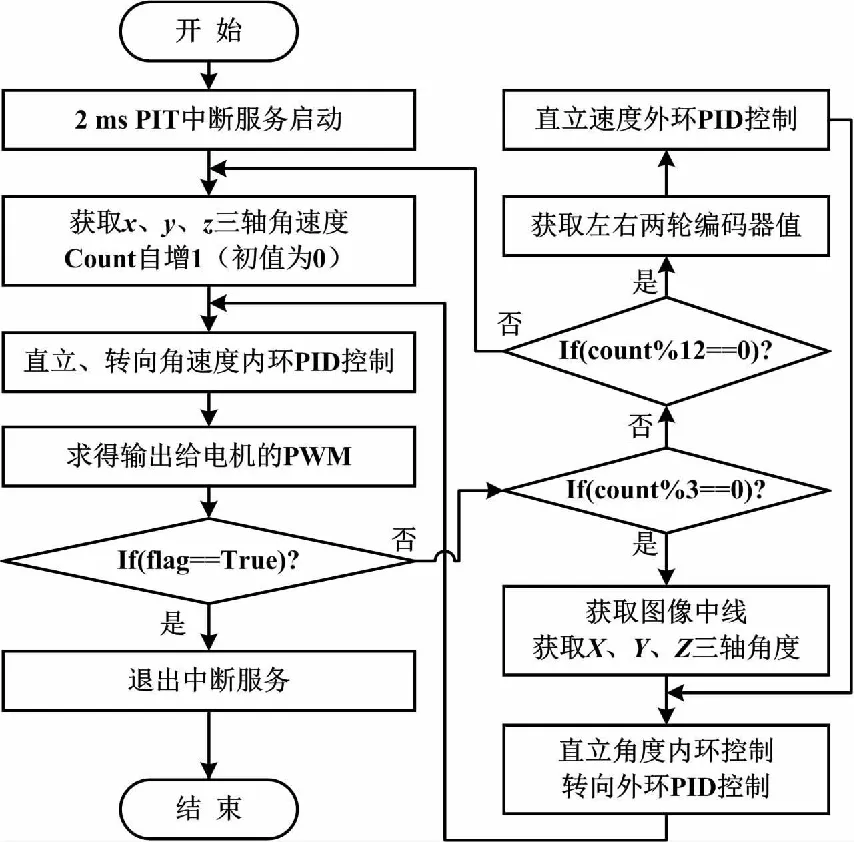
for(int i=VALUE; i {Turn_Error+=((m_line[i]-MIDDLE)* weight[i])/(sum_w*1.0);//图像权重法 m_l +=m_line[i];} Turn_Output=Turn_Kp * Turn_Error;//P控制 代码中,转向外环的输入为根据摄像头图像所计算的实际中线和设定的理想中线,对应到图像权重法中的m_line[i]和MIDDLE,将数字图像每行的列用一维数组表示,同时根据图像信息分布的不同划分权重占比[11]。for循环的[VALUE,CUT_H]为图像有效行区间。经大量试验测试,当系统机械零位、摄像头高度和角度确定后,VALUE取10效果较好,sum_w为有效行权重和。在离散化采样处理中,Turn_Error为当前时刻的中线偏差。 由于传感器的数据采集和各控制算法对实时性要求很高,故系统需要精准地把控控制周期。PID控制周期遵循最内环控制周期最短、最外环控制周期最长的原则。在工程应用中,外环周期约为内环周期的3~5倍。在单片机中并不需要利用多个周期中断定时器(periodic interrupt timer,PIT)定时中断,而是将控制周期都设置成2 ms的倍数,通过在一个2 ms中断服务程序中设置计数值,根据计数值的不同来调用不同控制周期的控制函数,从而实现相应的控制算法。定时器中断控制流程如图3所示。 图3 定时器中断控制流程图 经多次试验,本系统在串级直立行驶控制中:内环采样周期设定为2 ms;角度环设定为6 ms;速度环设定为24 ms。串级转向控制中,内环周期要与直立行驶控制内环周期相同,转向外环则设定为6 ms。 为简便经验调参步骤,避免单片机端参数需重复更改并下载的问题,本系统采用云端手机编程环境(APP Inventor)开发设计手机APP,进行辅助调参。APP Inventor是基于云端的手机编程环境,用户能通过该工具自行研发适合手机使用的任意应用程序。单片机端的HC-06主从一体式蓝牙,与手机蓝牙配对和相互通信。程序主要分为两部分:一是对单片机通过蓝牙接收的数据进行判断,如在上位机程序中设定发送字符(不同字符代表不同动作指令),从而控制两轮平衡车的各个环的参数调整和系统初始化;二是将手机端调试更改的参数反馈至单片机。 系统最终整定的各环PID配置参数如表1所示。表1中:参数的符号正负与PID的双极性有关。 表1 各环PID配置参数 本文设计的多回路PID控制下的两轮平衡车系统的创新点如下所示。 ①本系统更改了传统PID的控制结构,设计了以角速度环为主回路的双串级PID控制器,将速度和角度控制转换为角度和角速度控制;消除了原先速度PID与直立平衡PID并联所产生的耦合问题,提升了平衡车在高速行驶时的转向稳定性和姿态跟随能力。 ②卡尔曼滤波器算法进行数据融合时,本系统采用基于Visual C++的软件示波器进行卡尔曼滤波器的参数调试。上位机界面的交互性为参数整定过程提供了便利。 ③本系统采用APP Inventor开发设计的手机端APP来简便PID调参步骤。该APP开发编程效率高且易于操作,不需要过于复杂的算法和可视化界面编写;主从一体式蓝牙与手机交互通信,避免PID参数在单片机端更改和下载的麻烦。 本系统基于四旋翼飞行器的控制理论衍生的串级理论,设计了以角速度环为主回路的双串级PID控制,改善了传统PID控制器的结构,解决了两轮平衡车系统易受干扰、高速下稳定性和响应性差的问题。同时,对于数据融合的卡尔曼滤波器参数、PID参数的整定步骤,本文进行了交互性方面的简化,改善了相关参数调节的费力耗时问题。测试和试验结果表明,所设计的多回路控制下的两轮平衡车系统能够沿任意给定路径快速、稳定地行驶全程。相关算法可以推广至两轮平衡车相关领域,具有较为广阔的应用前景和丰富的研究价值。3.3 控制周期设定
3.4 手机蓝牙PID调参软件

4 创新点
5 结论

