燃气轮机启动过程故障诊断方法研究

张艾森

(上海工业自动化仪表研究院有限公司，上海 200233)

0 引言

当前，燃气轮机在工业领域和航空领域发挥了越来越重要的作用。在电力行业，燃气轮机的应用也成为主要发展趋势[1-3]。但是，随着燃气轮机工作环境的变化，尤其是启动过程中转速和温度均发生较大变化，各种故障将不断出现。为了确保燃气轮机的安全使用，燃气轮机启动过程故障诊断已成为当前的研究重点[4]。

由于燃气轮机内部结构较为复杂，当前故障诊断方法的应用存在诸多不足。文献[5]提出基于交叉全局人工蜂群和支持向量机(crossover global artificial bee colony and support vector machine，CGABC-SVM)的故障诊断方法，实时输出故障诊断结果，并考虑到参数信息变化对诊断结果的影响，结合人工蜂群算法优化参数，提升诊断准确率。但是，该诊断方法的泛化能力较差。文献[6]以改进深度信念网络(deep belief networks，DBN)为核心，建立诊断方法。该方法为了解决玻尔兹曼机模型的数据拟合问题，融合Dropout 技术和Adam 优化器，提升了故障诊断效率；采用随机梯度下降法进行反向微调，避免陷入局部最优解情况。但是，该诊断方法的容错性较低。文献[7]设计了基于深度学习与信息融合的故障诊断方法。该方法使用核主元分析技术处理原始数据，并从数据集中选取出主要表征参数；通过深度学习算法建立包含多个隐含层的诊断模型，自动获取故障数据中包含的关键信息，实现故障诊断的自动化。但该方法计算复杂度较高，故障诊断效率较低。

参考上述故障诊断方法，本文对燃气轮机启动过程进行深入分析，生成DBN故障诊断模型。试验结果表明，本文方法在实际应用中展现了更好的应用效果，有利于平均故障诊断错误率的降低。

1 故障诊断方法设计

1.1 故障样本数据抽取

燃气轮机的启动属于1种大范围变工况操作，具体包括盘车、启动、点火等多个步骤。燃气轮机启动各阶段分界情况如图1所示。

图1 燃气轮机启动各阶段分界情况图

由图1可知，燃气轮机启动过程中，冷、热加速阶段以点火为分界点，而热加速、自升速阶段则以脱扣为分界点。基于上述启动过程，本文针对典型启动故障进行模拟，获取启动过程故障发生后燃气轮机运行情况；通过不同故障程度的模拟，收集故障数据与近似故障数据。

考虑到上述样本数据不会受到主观因素影响而产生变化，为了确保故障诊断结果的准确性，从上述样本数据和正常数据中按比例选取大部分数据，将一部分数据标签清除后形成预训练样本数据集，另一部分则保留标签作为测试数据，输出故障诊断结果。为了降低诊断误差，本文采用极差归一化方法处理样本数据[8]。计算式为：

(1)

式中：xi为数据样本归一化处理结果；xi0为原始样本；xmin为样本数据集中最小数据；r为样本数据集极差。

通过式(1)，即可完成故障样本数据的处理，获取归一化数据样本值，作为故障诊断的数据基础。

1.2 典型启动故障特征提取

燃气轮机启动过程中如有故障问题，则会导致多种设备参数产生变化。因此，本文从机理入手，分析典型启动故障特征，并将此作为启动故障判断指标[9]。本文对喘振裕度、启动速度与加速度变化，以及燃料空气比进行研究，提取典型启动故障特征。

当燃气轮机发动机组与喘振区重合后，会产生喘振裕度。当压气机效率降低后，会出现热悬挂故障[10]。热悬挂故障发生概率随着喘振裕度的提升而增长。喘振裕度的计算式为：

(2)

式中：S为喘振裕度；K、L分别为某折合转速的不稳定边界点和工作点；πK为不稳定边界点的增压比；mK为不稳定边界点流量值。

由式(2)可知，喘振裕度值越大，表明运行与喘振边界之间的距离越大，则燃气轮机启动过程越安全。

燃气轮机启动过程中，需要注意的1项主要参数为启动速度与加速度变化。正常情况下，燃气轮机启动速度处于平稳状态。当转速上升速度较慢或产生停滞，表明燃气轮机启动出现故障，需要工作人员立即停机检查。

最后1项典型启动故障特征是燃气轮机启动过程中燃料空气比变化。作为评估燃烧室性能的主要参数，其计算式为：

(3)

式中：f为燃料空气比；λ为1 kg燃料对应的实际控制量。

开始点火后，当燃料空气比处于正常状态时，燃气轮机启动正常。当燃料空气比低于正常范围时，极易发生点火失败。所以，在启动故障诊断过程中，需要计算燃料空气比，并将其与实际启动工程相比较，从而确定故障状态。

1.3 DBN诊断模型设计

本文以DBN结构为基础，构建故障诊断模型。DBN属于非监督深层网络结构，由多个径向基网络(radial basis network，RBN)共同组成。每个RBN由可视层与隐含层2部分组成。1个RBM包含的能量计算式为：

(4)

式中：E为RBN能量值；v为网络可视层结构；h为网络隐含层结构；i、j为网络神经元；ci为可视层偏置量；bj为隐含层偏置量；ω为神经元连接权重；vi为可视层神经元状态；hj为隐含层神经元状态；θ为RBN的结构参数；V为可视层神经元总数；H为隐含层神经元总数。

RBN中，可视层和隐含层内的神经元均处于独立状态。当隐含层状态确定后，可视层神经元激活概率计算式为：

(5)

式中：P为激活概率；φ为sigmoid激活函数。

反之，可视层神经元状态确定后，隐含层激活概率为：

(6)

式(5)与式(6)分别为逆向学习和正向学习。学习过程中，连接权重值更新式为：

Δωij=α[O(vihj)-G(vihj)]

(7)

式中：α为学习率；O为网络训练目标；G为训练模型输出结果。

本文设计的诊断模型由3个RBN组成。包含3个RBN的DBN结构如图2所示。

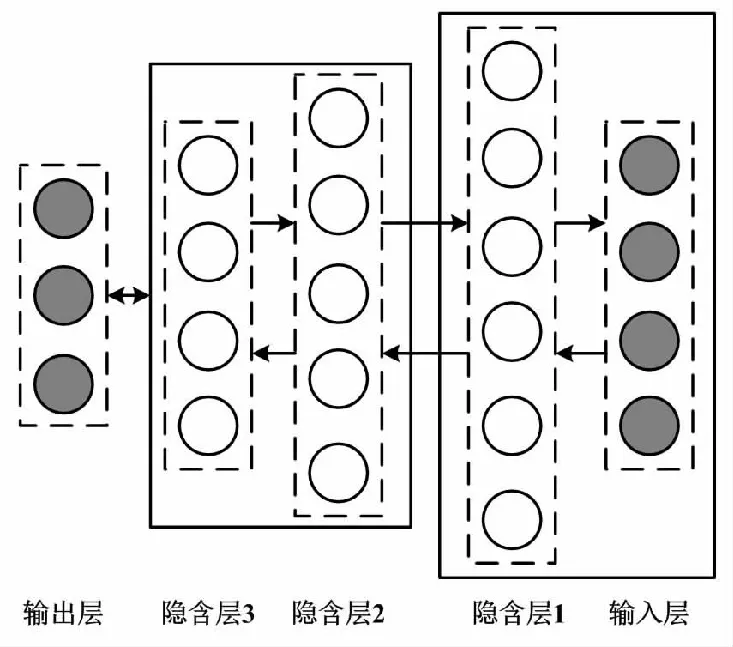
图2 包含3个RBN的DBN结构图

图2中：有色节点为输入层和输出层的神经元；无色节点为隐含层1～3的神经元。

利用图2所示的DBN结构进行燃气轮机启动过程故障诊断，主要包含以下2个操作步骤。首先是非监督式学习，通过输入层、隐含层、输出层3个环节完成每个RBN的训练，获取深度信念网络初始结构参数[11]。其次是采用监督式反向学习模式，合理调整DBN结构参数[12]。RBN通过独立训练生成最优化参数，计算式为：

(8)

式中：M为染色体个数。

结合对比散度生成连接权重、可视层偏置量、隐含层偏置量更新条件：

(9)

式中：ε为对比散度。

RBN训练结束后，通过反向微调优化结构参数，实现故障诊断模型的训练误差降低。训练误差计算式为：

(10)

式中：μ为训练误差；L为训练样本；Y为分类器输出。

根据式(10)计算结果，将训练误差与训练误差预期要求作对比，不断调整结构参数，直到训练误差满足故障诊断要求。

1.4 启动故障诊断实现

应用上述诊断模型可以得到燃气轮机启动过程故障诊断结果。在实现过程中，考虑到局部最优解现象的出现，因此建立以列文伯格-马夸尔特(Levenberg-Marquardt,L-M)算法为核心的自适应学习技术，去除DBN中误差函数曲面上非最小误差值节点。L-M算法的应用结合了梯度法和高斯牛顿法，采用均方误差充当损失代价函数，得出误差梯度：

ζ(θ)=J(θ)e(θ)

(11)

(12)

式中：a为雅克比矩阵行数；z为雅克比矩阵列数。

在L-M算法的基础上，生成以下DBN结构参数更新式：

θw+1=θw-JwIw

(13)

式中：w为迭代次数；Jw为以网络学习误差函数为核心的迭代雅克比矩阵；Iw为迭代误差向量。

通过上述操作，可降低故障诊断结果错误率，获取高精度燃气轮机启动过程故障诊断结果。

2 试验

为了验证本文设计方法的应用效果，通过试验的方式得到燃气轮机启动过程故障诊断结果。考虑到燃气轮机结构较为复杂，产生启动故障的原因多种多样，本文采用MATLAB工具开发试验环境，验证本文设计诊断方法的有效性。

2.1 试验样本选取

为了维护燃气轮机启动正常，气路截面压力、燃机转速等多种参数的监控是不可或缺的。本文按照参数表征性和冗余性选取试验样本，确定排气温度、电机电流、燃机转速和电机转速这4种参数类型。同时，每种参数选择部分正常数据和小部分故障数据，汇总形成试验样本，作为故障诊断方法测试的数据基础。上述4种参数采集过程中，以启动过程中某一时刻为参考，分析相同时刻不同参数值，生成启动过程的特征向量。

参数样本分布如图3所示。

图3 参数样本分布图

图3中，每个参数的分布均处于均匀状态，表明试验样本具有较强的表征性。

2.2 诊断模型参数设置

本文设计的故障诊断方法以DBN为基础，所以网络诊断模型参数的研究是试验进行的前提。根据本文设计可知，堆叠3个RBN单元构成整体故障诊断模型。为了确定DBN模型的具体结构，分析隐含层节点数量发生变化时，不同隐含层节点个数对应的训练误差如图4所示。由图4可知： RBN1、RBN2和RBN3的隐含层节点分别为93个、43个和19个时，训练误差最小。

图4 不同隐含层节点个数对应的训练误差

根据上述得出的最优隐含层节点数量，构建如图5所示的DBN故障诊断模型。

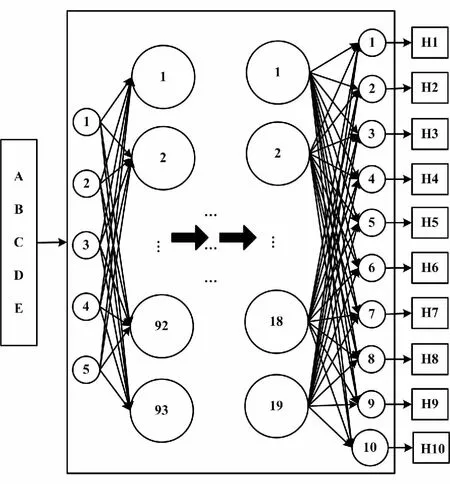
图5 DBN故障诊断模型

DBN参数配置如表1所示。

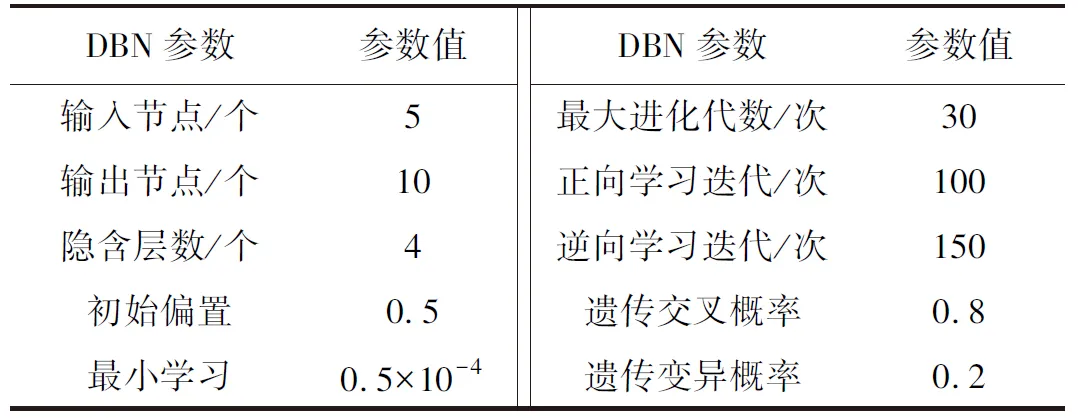
表1 DBN参数配置

除了上述参数外，本文按照标准DBN学习特点，将初始学习率设置为0.6。诊断模型参数设置完成后，将试验样本应用于模型中，获取燃气轮机启动过程故障诊断结果。

2.3 故障诊断结果对比

为了加强试验结果的真实性，将试验数据集分别应用于本文方法、CGABC-SVM故障诊断方法以及深度学习与信息融合诊断方法中，并将不同方法的识别结果以混淆矩阵的形式表现出来。

不同方法诊断结果的混淆矩阵如图6所示。

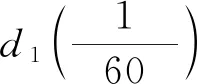
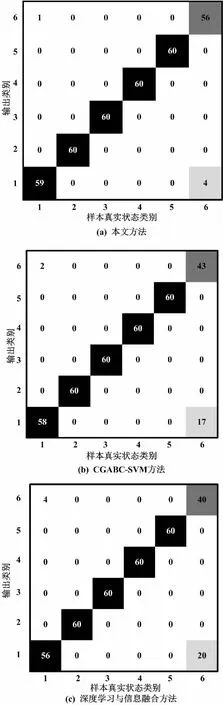
图6 不同方法诊断结果的混淆矩阵

(14)

式中:eerror为平均故障诊断错误率;R为识别误差样本数;N为样本总数。

由式(14)可知，本文设计方法的平均故障诊断错误率为3.3%，相比其他方法将平均故障诊断错误率降低了28.7%、37.0%。综上所述，本文设计的故障诊断方法有效提升了燃气轮机启动过程故障诊断结果的准确性。

3 结论

本文针对燃气轮机启动故障进行研究，提出以DBN结构为核心的燃气轮机启动故障诊断方法。该方法选取排气温度、电机电流、燃机转速和电机转速这4种参数类型作为样本数据和特征数据，构建启动过程的特征向量。通过分析不同隐含层节点数量的训练误差波动情况，确定了DBN的最优参数配置，构建了DBN燃气轮机启动故障诊断模型。经由模型得出的故障诊断试验结果可知，本文设计方法的平均故障诊断错误率为3.3%，相比CGABC-SVM故障诊断方法以及深度学习与信息融合诊断方法，本文提出的DBN模型将平均故障诊断错误率降低了28.7%、37.0%，有效提升了燃气轮机启动过程故障诊断结果的准确性。

针对本文中所提出的诊断方法需要注意的一点是，该方法得出的故障诊断结果对于未出现过的故障类型还无法识别。此外，DBN的结构调整一定程度上依赖于人为经验。这些问题都将是未来主要研究方向。