不连续驱动-响应网络的固定与预定时间同步

李兴瑞，肖玉柱，宋学力，赵楠楠，史东鑫，单美华

长安大学理学院，陕西西安 710064

复杂网络是一种数据表现形式与科学研究手段，现实生活中的互联网［1］、神经元网络［2］及生物网络［3］等实际系统，均可以通过复杂网络建模后进行分析描述．复杂网络同步是复杂网络动力学行为［4］中的重要内容，在生物工程、信息处理及保密通信等领域具有广阔应用空间［5］．固定时间同步的同步时间估计因无需依赖系统的初值特性而受到学者的广泛研究关注［6］．预定时间同步的同步时间可以根据实际需要提前指定，不受系统初始值和控制参数的影响，更符合实际应用场景．

目前的研究大多关注具有连续动态节点的复杂网络［7］，而不连续现象在实际生活中普遍存在［8］，在处理含有非线性和高坡度的复杂网络时，不连续现象也不可忽略．ZHANG等［9］基于量化控制分析不连续复杂网络的固定时间同步问题；GAN等［10］利用间歇控制器研究有向社区网络的固定时间同步问题；HU等［11］通过改进的固定时间稳定性定理，研究不连续复杂网络的固定时间与预定时间同步，其同步时间估计式由特殊函数表示，计算较繁琐；GAN等［12］基于连续系统利用比较原理设计了更宽松的稳定性条件，但其对同步时间估计的精确度仍有待提高．以上研究均针对网络的内同步，对于驱动-响应网络同步的研究也是有必要的．LI等［13］研究具有不连续节点和噪声干扰的驱动-响应网络概率固定时间同步，但是对固定时间的估计与实际相差较远．LIU等［14］设计了控制增益为时变无界的光滑控制方案，并研究复杂网络的预定时间集群同步，但这种控制策略在实践中很难实现．

本研究在HU等［11-12］的理论基础上，给出表达式更简单且对稳定时间估计更准确的固定时间稳定性定理．通过设计不含线性反馈项的简单控制器，运用右端不连续微分方程理论，非光滑分析讨论了具有不连续激活函数的驱动-响应网络固定时间同步问题．运用固定时间稳定性定理的推论，提出有限增益控制策略，研究具有不连续激活函数的驱动-响应网络预定时间同步问题，其同步时间可以根据实际情况预先指定，与系统初始值和控制器参数无关．

1 不连续系统的固定时间稳定性定理

考虑如下不连续系统［15］

其中，x∈Rn，f(x)：Rn→Rn是不连续但局部可测的，且f(0)=0.

定义1［16］如果函数x(t)在[0，t*)上有定义且在其任意紧区间上绝对连续，并满足微分包含

则称函数x(t)为系统（1）的1个Filippov解，其中，集值映射K[f]：Rn→Rn定义为

其中，cˉoˉ为凸闭包；μ为Lebesgue测度；B(x，ε)是以x为中心、ε＞0为半径的开领域；S∈Rn是测度为0的任意集合．

引理1［17］如果V(x)是C-正则（正则、正定及径向无界）的，x()t：［0，+∞］→Rn在［0，+∞］上的任意紧区间是绝对连续的，则x(t)和V(x)在t∈［0，+∞］上几乎处处可微，且满足其 中 ， ∂V(x(t))=表示V的广义梯度；co表示凸包；ΩV∈Rn表示V的1组不可微点．

引 理2［11］若 存 在C-正 则 函 数V(x(t))：Rn→R及 常 数k∈R，α＞0，β＞0，δ＞1，0≤θ≤1，满足

则系统（1）是固定时间稳定的，且以下结论成立：

1）当k≤0时，其稳定时间T(x0)满足

2）当0＜k＜min{α，β}时，其 稳 定 时 间T(x0)满足

其中，定义I(x，p，q)=为不连续贝塔函数比；0≤x≤1；p＞0；q＞0；表示贝塔函数．

引 理3［12］如果系统（1）中 的 函 数f(x)：Rn→Rn是连续的，且存在1个正的径向无界函数V(x(t))：Rn→R满 足 式（3），其 中，常 数k＜min{α，β}；α＞0；β＞0；δ＞1；0≤θ≤1，则该系统是固定时间稳定的，且以下结论成立：

1）当k≠0时，其稳定时间T(x0)满足

2）当k=0时，其稳定时间T(x0)满足

基于引理2和引理3的条件与结论，针对不连续系统，以下给出时间估计更精确的固定时间稳定性定理．

定理1若存在C-正则函数V(x(t))：Rn→R满足

其中，常数k＜min{α，β}，α＞0，β＞0，δ＞1，0≤θ≤1，则该系统是固定时间稳定的，且以下结论成立：

1）当k=0时，其稳定时间T(x0)满足

2）当k≠0时，其稳定时间T(x0)满足

【证】由引理2可知，系统（1）是固定时间稳定的，以下给出时间估计的证明．

1）当k=0时，式（3）成立，即

由引理2及文献［11］中的证明可知，稳定时间满足通过变量代换令可得

2）当k≠0且k＜min{α，β}时，为不失一般性，假设V(x0)＞1提出以下分段微分方程：

比较式（3）与式（12）可得，0≤V(t)≤W(t)．因此，如果存在时间T＞0使得=0且t＞T时有W(t)≡0，则当=0且t＞T时，有V(t)≡0．

当W(t)≥1时，令U(t)=W1-θ(t)．由式（12）容易看出当W(t)→1+时，U(t)→1-．因此，能够得到

当0≤W(t)＜1时，令U(t)=W1-θ(t)．由式（13）容易看出当W(t)→0+时，U(t)→0+，可得

因此，系统（12）的固定时间稳定性问题转化为系统（13）和系统（14）的收敛问题，即在固定时间T͂内，系统（13）的解趋向于1；在固定时间-T内，系统（14）的解趋向于0．因此，对于任意初值W(0)，在固定时间内，W(t)→0．

对于0＜k＜min{α，β}，首先估计时间͂，使得式（13）中的U(t)趋于1．

由V(x0)＞1知U(0)＜1，从式（13）可得

从0＜U(0)＜1，和0可知，存在时间T͂＞0，当0＜t＜T͂时，有＜1，且有

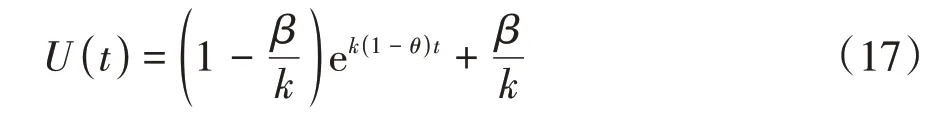
从U(0)=1，和＜0可知，存在时间＞0，满足=0，且有

结合式（16）和式（18）能够看出，对于任意的初值W(0)，在固定时间内，均有W(t)→0．因 此，对 于有W(t)≡0成 立，即 有V(t)≡0成立．

当k＜0时的证明与上述类似．

由 以 上 证 明 过 程 可 见，当k≠0且k＜min{α，β}时，不连续系统（1）是固定时间稳定的，且其稳定时间估计为．证毕．

近来针对连续系统［12］、不连续系统［11］及随机系统［13］的固定时间稳定问题进行了深入研究．固定时间稳定研究的核心问题是估计系统的稳定时间，定理1在上述研究成果的基础上进一步给出了更准确的稳定时间估计．当k=0时，定理1中的固定时间估计与文献［11］相同，优于文献［13］的结果；当k≠0时，文献［11］中的固定时间估计式用特殊函数表示，定理1的固定时间估计用常见的对数函数表示，且固定时间估计式比文献［11，13］更精确．

由定理1可以得出以下预定时间稳定性推论．

推论1对于不连续系统（1），如果存C-正则函数V(x(t))：Rn→R满足

其中，常数k＜min{α，β}；α＞0；β＞0；δ＞1；0≤θ≤1；Tp＞0．则系统（1）在指定时间Tp内达到稳定，其中

推论1中的Tp与其他参数k、α、β、δ及θ均无关．这种不相关性为探索网络的预定时间同步提供了思路．针对不连续系统，本研究提出的定理1具有比引理1更精确的稳定时间估计，为解决具有不连续激活函数网络的固定时间与预定时间同步提供了理论基础．

2 驱动-响应网络的固定时间与预定时间同步

2.1 问题陈述

考虑一类具有N个节点的复杂网络，描述为

将网络（21）视为驱动网络，则相应的受控响应网络描述为

其中，ui(t)为待设计的控制器．

下面给出响应网络（22）固定时间与预定时间同步于驱动网络（21）的定义．

定义3令ei(t)=yi(t)-xi(t)为系统误差．若存在与网络和控制器参数有关而与初值无关的时间T*， 使 得， 且 对 于t＞T*有≡0，称响应网络（22）固定时间同步于驱动网络（21）；若时间T*是预先指定的时间，与网络和控制器参数及初始值均无关，则称响应网络（22）预定时间同步于驱动网络（21）．

由于网络中含有不连续激活函数，给出以下2个假设条件．

假设1对于fj，j=1，2，…，n，除在可数个孤立点外均连续，其左右极限和存在，且fj在任意有界紧区间上至多存在有限个跳跃间断点．

假设2对每个j=1，2，…，n，存在非负常数Lj和Mj，使得对任意u，v∈Rn满足

引理4［18］设a1，a2，…，an为非负常数，0＜p≤1，q≥1，以下不等式成立

2.2 驱动-响应网络的固定时间同步

本节应用定理1中改进不连续系统的固定时间稳定性，解决具有不连续激活的驱动-响应函数网络固定时间同步问题．在以往的同步结果中，线性部分是在控制器设计中必不可少．与这些控制方案不同的是，本研究在没有线性反馈项的情况下，通过1个更简单的控制器来实现驱动-响应网络的固定时间同步．所设计的控制器为

其 中 ，δ＞1；φ＞0；α＞0；Sign(ei(t))=sign(ei1(t))表示ei1(t)的符号函数；

定理2令λ为矩阵c(As⊗Γ)+(IN⊗L)的最 大 特 征 值，其 中；⊗表示Kronecker积．控制器为式（25），假设1和假设2成立，如果满足

则称响应网络（22）固定时间同步于驱动网络（21），且以下结论成立：

1）当λ=0时，同步时间满足

2）当λ≠0时，同步时间满足

【证】根据微分包含理论，系统（21）和（22）的解分别满足

因此，相应的误差系统为

构造如下Lyapunov函数

对于e(t)∈RnN{0}，可得

其中，

基于假设2可得

由引理4也可得

将式（35）至式（38）带入式（34）可得

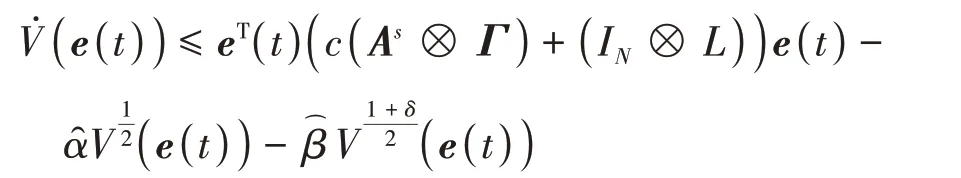
由于λ为矩阵c(As⊗Γ)+(IN⊗L)的最大特征值，故上式可表示为

由定理2可知，响应网络（22）在固定时间内同步于驱动网络（21）．证毕．

2.3 驱动-响应网络的预定时间同步

预定时间同步的同步时间可以根据实际需要提前指定，不受任何系统初始值和控制参数的影响，相比固定时间同步具有更广阔的应用前景．目前对于具有不连续激活函数网络预定时间同步的研究成果较少，HU等［11］提出控制增益有限的控制协议，实现了不连续网络的预定时间同步，但其对于时间的分类比较繁琐．与LIU等［14］的研究结果不同，本研究基于推论1，提出一种有限增益控制策略，实现具有不连续激活函数的驱动-响应网络预定时间同步，其适用性更广，对于时间的分类方式更简单．所设计的控制器为

其中，δ＞1；α＞0；φ＞0；Tp＞0是根据实际预先指定的时间．

定理3在假设1、假设2及控制器（39）下，条件（26）与式（27）仍成立，λ、L及M均如定理2中所定义，则称响应网络（22）在预定时间Tp内同步于驱动网络（21）．

【证】Lyapunov函数同式（33），类似的可以得到

与定理2的证明类似，可以得到

由引理4可得

结合定理2的证明，将式（41）和式（42）带入式（40）可知

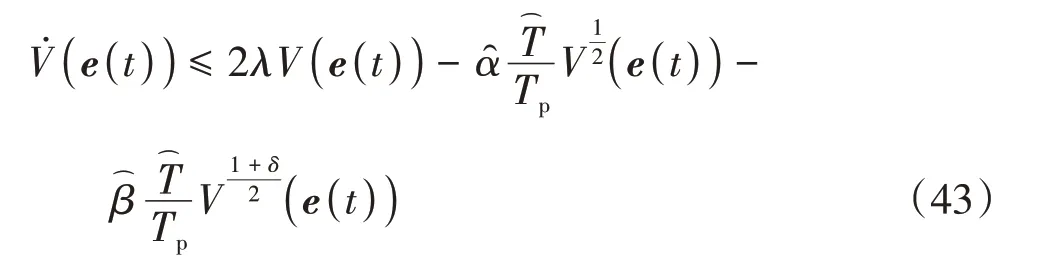
当λ≤0时，式（43）可以写为

此时由推论1可知，网络（22）在预定时间Tp内同步于网络（21）．

当λ＞0时，若有Tp＜，则式（43）可以改写为

此时由推论1可知，网络可在预定时间Tp达到同步．若≥Tp，根据定理2，网络在时间内已经达到同步，因此，在预定时间Tp内也达到了同步．证毕．

3 数值模拟

以下给出2个数值例子分别验证不连续系统固定时间稳定性理论的正确性，及固定时间与预定时间同步策略的有效性．

例1不连续系统的稳定时间估计

考虑如下不连续系统

选 择 参 数K=diag{0，0，0}，Θ=diag{1.0，1.2，1.0}，Ω=diag{1.1，1.2，1.0}，(δ，θ)=( 1 .5，0.2)．由定理1中的结论（1）可以得出，系统（44）是固定时间稳定的，数值模拟结果如图1．本研究得出的稳定时间估计值为T1=3.6240 s，在此参数下，文献［12］得出的稳定时间估计值T2=4.7141 s，文献［13］中给出的稳定时间估计值T＇=5.6287 s．定理1给出的时间估计更精确．

图1 参数K=diag{0，0，0}时系统（44）的稳定性Fig.1 Stability of system(44)with parameter K=diag{0,0,0}.

选择另一组参数K=diag{0.6，0.4，0.5}，Θ=diag{1.7，1.6，1.8}，Ω=diag{1.3，1.2，1.3}，(δ，θ)=(1.6，0.3)，由定理1中的结论（2）可得，系统（44）是固定时间稳定的，数值模拟结果如图2．本研究得出的稳定时间估计值为T3=6.5127 s，小于文献［11］中给出的同步时间估计值T4=7.5588 s，文献［13］给出的稳定时间估计值为T″=66.6604 s，远大于实际稳定时间．可见，本研究给出的稳定时间估计更精确．

图2 参数K=diag{0.6，0.4，0.5}时系统（44）的稳定性Fig.2 Stability of system(44)with parameter K=diag{0.6,0.4,0.5}.

例2驱动-响应网络的固定与预定时间同步．考虑如下具有不连续激活函数的网络

其对应的受控响应网络为

网络的外接耦合矩阵为

网络（45）和（46）的初始值均为随机数．根据假设2取Lj=1，Mj=0.03，因此，L=I3，M=0.03.

在控制器（25）下，选择控制参数(α，φ，δ)=(2.0，2.0，1.4)和(α，φ，δ)=（2.2，4.0，1.5），由定理2可知，响应网络（46）分别在估计时间T5=3.8505 s，T6=1.7538 s内同步于驱动网络（45）．数值模拟结果如图3和图4，与理论结果相符，验证了控制器的有效性与定理2的正确性．

图3 参数为(α，φ，δ)=(2.0，2.0，1.4)时的同步误差曲线Fig.3 Synchronization error curve for(α,φ,δ)=(2.0,2.0,1.4).

图4 参数为(α，φ，δ)=(2.2，4.0，1.5)时的同步误差曲线Fig.4 Synchronization error curve for(α,φ,δ)=(2.2,4.0,1.5).

验证定理2中同步时间估计式的精确性．选择控制参数(α，φ，δ)=(2.8，2.4，1.6)，由定理2可知，响应网络（46）在估计的同步时间T7=3.2936 s内同步于驱动网络（45）．在相同参数下，文献［11］估计的同步时间为T8=4.3853 s；文献［13］估计的同步时间为T9=37.4546 s.文献［19］的数值模拟例3中模拟了没有噪声干扰情况下，不连续驱动-响应网络的固定时间同步，误差系统在t=0.21 s时实现稳定，而其估计时间为T=190 s，远大于实际同步时间．本研究同步误差模拟结果如图5，响应网络（46）在更小的时间T7内与驱动网络（45）实现同步，表明本研究对于同步时间估计的精确度更高．

图5 参数为(α，φ，δ)=(2.8，2.4，1.6)时的同步误差曲线Fig.5 Synchronization error curve for(α,φ,δ)=(2.8,2.4,1.6).

为验证预定时间同步控制器的有效性，在控制器（39）下，选择控制参数(α，φ，δ，Tp)=（3.0，2.0，1.3，2.0）和(α，φ，δ，Tp)=（3.0，2.0，1.3，2.0）．根据定理3，响应网络（46）将在预定时间Tp内同步于驱动网络（45）．数值模拟结果如图6和图7，网络均在预先指定的时间Tp内达到同步，验证了定理3的正确性．

图6 参数为(α，δ，φ，Tp)=(3.0，2.0，1.3，2.0)时的同步误差曲线Fig.6 Synchronization error curve for(α,δ,φ,Tp)=(3.0,2.0,1.3,2.0).

图7 参数为(α，φ，δ，Tp)=(2.0，3.0，1.6，0.5)时的同步误差曲线Fig.7 Synchronization error curve for(α,φ,δ,Tp)=(2.0,3.0,1.6,0.5).

结语

本研究针对不连续系统，给出了一个同步时间估计更精确的固定时间稳定性定理，并应用该定理研究具有不连续激活函数的驱动-响应网络固定及其时间同步问题．以HU等［11］的稳定性定理为基础，利用比较原理和变量代换得到更新的稳定时间估计式．数值模拟结果表明，本研究对于稳定时间的估计表达式更简单，结果更精确．利用所得到的定理进一步实现具有不连续激活函数的驱动-响应网络固定时间和预定时间同步，所使用的控制器不包含常见的线性反馈项，且对于同步时间的估计更精确，所提出的有限增益控制策略比现有的无限增益控制策略更有效．本研究固定时间稳定性定理与有限增益控制方法还可用于探索多智能体模型的固定时间与预定时间共识，此类问题将是后续的研究重点．