双孔双渗油藏斜井压力动态特征分析
聂仁仕,贾冉,蔡明金,李洪,卢聪,杨岚
1)西南石油大学油气藏地质及开发工程国家重点实验室,四川成都 610500;2)中石油天然气股份有限公司塔里木油田分公司勘探开发研究院,新疆库尔勒 841000;3)中石油天然气股份有限公司塔里木油田分公司轮南油气开发部,新疆库尔勒 841000
裂缝性油藏是指发育有大量裂缝的油藏,其储层具有较强的非均质性,渗流机理复杂,实现裂缝性油藏高效开发难度较大.油井井底压力动态特征的变化取决于流体在地层中的渗流规律以及油井产能大小.因此,开展斜井井底压力动态特征分析,不仅有利于认识地下流体的渗流规律,也能更准确地分析油井产能大小,为实现裂缝性油藏高效开发奠定理论基础.
关于斜井渗流模型的研究,CINCO等[1-5]建立了均质油藏斜井渗流模型,并求出其井底压力解、绘制压力动态曲线.后来,点源函数法成为了研究斜井渗流模型的热门方法;李巍等[6-8]利用此方法对斜井井底压力动态的变化进行了研究.随着研究热点从均质油藏变为双重介质油藏,ZHANG等[9-15]先后建立和求解了双重介质油藏直井、水平井以及压裂水平井的渗流模型,并绘制得到了压力动态特征曲线.关于双重介质油藏斜井的研究,廖新维等[16-18]给出了双重介质斜井的压力解表达式,但均未考虑双渗流动情况.随着研究的进一步深入,田冀等[19]采用数值模拟的方法研究了双重介质油藏直井双渗渗流模型,并对实例井进行了分析;蔡明金等[20-22]分别建立和求解了双孔双渗油藏直井、水平井渗流模型,绘制和分析了其压力动态特征曲线.文献调研发现,双孔单渗油藏斜井渗流模型已有很多相关研究报道,关于双孔双渗直井和水平井渗流模型也有研究报道,但尚未见到双孔双渗斜井渗流模型的相关文献.
基于此,本研究建立了双孔双渗油藏斜井渗流模型,该模型利用有效井径的方法考虑斜井表皮系数,同时利用杜哈美叠加原理考虑井筒储集系数,采用Laplace变换等数学方法对模型进行求解,并研究了模型解的井底压力动态响应特征.
1 物理模型
本研究物理模型如图1所示,假设条件如下:①斜井以定产量q生产,生产前地层中各点的压力均匀分布;②地层水平、等厚,且上下边界均为不渗透边界,外边界为无穷大,地层厚度为h;③斜井井长为L,井筒半径为rw,井的斜角为θ,井中心距地层下边界的垂直距离为zw;④地层原油和岩石均微可压缩,压缩系数为常数;⑤地层单相原油作等温达西渗流;⑥假设地层为天然裂缝发育的Warren-Root双重介质模型,且考虑基质系统流体同时向天然裂缝系统和井筒流动的双渗流动情形;⑦地层水平渗透率和垂直渗透率不相等.

图1 双孔双渗油藏斜井物理模型 (a)斜井物理模型图;(b)双孔双渗示意图Fig.1(Color online)Physical model of a slanted well in a dual-porosity and dual-permeability reservoir,in which(a)is a slanted well in fractured reservoir and(b)is a slanted well with the dual-porosity and dual-permeability feature.
2 数学模型
2.1 有因次数学模型
裂缝系统渗流控制偏微分方程为

基质系统渗流控制偏微分方程为

无因次裂缝压力为

无因次基质压力为
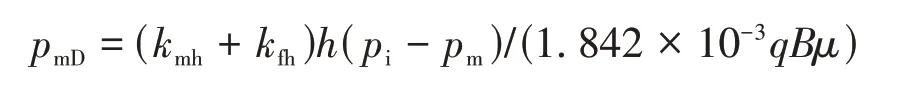
弹性储容比为

窜流系数为

裂缝与总系统渗透率比为

斜井表皮系数为

类似直井表皮系数为

无因次径向坐标为

无因次垂向坐标为

无因次储层有效厚度为

无因次时间为

初始条件为

点源生产内边界条件为

顶底封闭边界条件为

无限大地层外边界条件为

其中,pi为初始地层压力,单位:MPa;pf为裂缝压力,单位:MPa;pm为基质压力,单位:MPa;Δps为表征油井污染的附加压力损失,单位:MPa;r为径向坐标,单位:m;rw为井半径,单位:m;z为垂向坐标,单位:m;zw为垂向井筒位置坐标,单位:m;h为地层厚度,单位:m;L为斜井长度,单位:m;t为生产时间,单位:h;km为基质渗透率,单位:μm2;kfh为裂缝水平渗透率,单位:μm2;kmh为基质水平渗透率,单位:μm2;kfp为裂缝垂向渗透率,单位:μm2;kmp为基质垂向渗透率,单位:μm2;μ为原油黏度,单位:mPa·s;φf为无因次裂缝孔隙度;φm为无因次基质孔隙度;Cft为裂缝弹性综合压缩系数,单位:MPa-1;Cmt为基质弹性综合压缩系数,单位:MPa-1;αm为基质块的形状因子,单位:m-2;q为斜井产量,单位:m3/d;B为无因次地层原油体积系数;θ为斜井的斜角,单位:(°);ε为垂向无穷小变量,单位:m.
2.2 无因次数学模型
裂缝系统渗流控制偏微分方程为

基质系统渗流控制偏微分方程为

初始条件为

点源生产内边界条件为

顶底封闭边界条件为

无限大地层外边界条件为

2.3 数学模型求解
1)拉氏变换
基于时间tD的拉氏变换关系式为

对式(8)和式(9)无因次数学模型进行拉氏变换,得

2)分离变量
采用分离变量法,对拉氏空间中的数学模型进行求解,设

将式(22)分别代入式(16)和式(17),进行变量分离,得

其中,pˉD为拉氏空间下的无因次压力;u为拉氏变量;Rˉj为压力在水平径向方向上的分量变量;Zˉj为压力在垂向方向上的分量变量;f和m为分别代表裂缝和基质;ξ为中间代换变量;τ为-Zj的特征值;σ为中间代换变量.
3)水平径向方向的解
水平方向渗流与垂向无关,将式(23)代入式(16)和式(17),得

其中,m1=-(λ+uω)e-2S,m2=λe-2S,m3=-[λ+u(1-ω)]e-2S.
式(26)和式(27)的通解分别为

将式(28)和式(29)代入式(21),得

将式(28)和式(29)分别代入式(26)和式(27),可将模型的通解变为


将通解式(31)和式(32)分别代入式(18)和式(21),可求得

4)垂向方向的解
将式(24)代入式(19)和式(20),得

其中,无因次垂向井筒位置坐标为zwD=zw/h;τn为在顶底封闭边界条件下的特征值.
5)点源模型的解
将式(31)和式(35)分别代入式(22),得井底点源生产引起的裂缝系统压力解为

6)斜井模型的解
将点源解沿斜井井筒积分,得斜井定产量生产井底压力解为

根据图2的微元变换关系,式(37)可变为

图2 微元变换关系示意图Fig.2(Color online)Schematic diagram of the transformation relation of micro element.

利用杜哈美叠加原理,可求得考虑井筒储集效应的斜井定产量生产井底压力解为

其中,无因次井筒储集系数为CD=Cs/[6.2832φ(φmCmt+φfCft)hr2w];lD为无因次井筒长度;xD为水平面内无因次x坐标;为拉氏空间下不考虑井筒储集效应的井底压力解;-pwD为拉氏空间下考虑井筒储集效应的井底压力解;Cs为井筒储集系数,单位:m3/MPa.
最后,利用Stehfest方法[23]对式(39)进行数值反演,可获得实空间中的井底压力解.
3 井底压力动态特征分析
3.1 渗流流动阶段识别
利用模型的解,采用Matlab软件编程绘制出典型的双孔双渗油藏斜井的压力动态特征曲线(图3).从图3中可以看出,压力动态特征曲线可以划分为7个流动阶段:①第Ⅰ阶段为纯井筒储集效应阶段;②第Ⅱ阶段为表皮效应阶段,压力导数曲线呈“驼峰”状;③第Ⅲ阶段为早期径向流阶段,压力导数曲线呈水平线;④第Ⅳ阶段为中期线性流阶段,压力导数曲线呈一定斜率的直线;⑤第Ⅴ阶段为过渡流阶段;⑥第Ⅵ阶段为基质系统流体向裂缝系统窜流阶段,压力导数曲线呈V形状凹子;⑦第Ⅶ阶段为晚期基质与裂缝系统整体径向流阶段,压力导数曲线呈水平线.

图3 典型井底压力动态特征曲线Fig.3(Color online)Typical bottom hole pressure dynamic characteristic curves.
3.2 斜井、直井与水平井压力动态特征曲线比较
图4为双孔双渗油藏斜井、直井与水平井压力动态特征曲线对比图.与直井相比,斜井多了早期径向流阶段和中期线性流阶段.与水平井相比,斜井早期径向流阶段和中期线性流阶段的持续时间均小于水平井.直井、斜井和水平井的压力特征曲线逐次变低,这是因为从直井到水平井,开发井的泄油面积逐渐变大,在相同的产量生产模型假设条件下,泄油面积越大所需要的井底压降越小,无因次压力曲线位置也就越低.

图4 斜井、直井与水平井压力动态特征曲线对比Fig.4(Color online)Comparison diagram of pressure dynamic characteristic curves of①the slanted well,②the vertical well,and③the horizontal well.
3.3 曲线敏感性分析
图5 为井斜角θ对双孔双渗油藏斜井压力动态特征曲线的影响.从图5可见,随着θ增大,压力及压力导数曲线依次变低.井斜角主要影响表皮效应阶段、早期径向流和中期线性流动阶段压力导数曲线特征的观察.井斜角越大,早期径向流和中期线性流动阶段就越明显.

图5 井斜角对压力动态特征曲线的影响Fig.5(Color online)Influence of inclination angle of well on pressure dynamic characteristic curves.
图6为斜井井长L对压力动态特征曲线的影响.从图6可见,L对表皮效应阶段、早期径向流阶段和中期线性流阶段的压力动态特征曲线产生明显的影响.井长越长,压力及压力导数曲线位置越低,中期线性流持续时间越长.

图6 斜井井长对压力动态特征曲线的影响Fig.6(Color online)Influence of length of slanted well on pressure dynamic characteristic curves.
图7为裂缝系统与总系统渗透率比值κ对压力动态特征曲线的影响.从图7可见,κ值的大小明显对表皮效应阶段、早期径向流阶段、中期线性流阶段及窜流阶段的压力动态特征曲线产生影响.κ值越大,基质系统和裂缝系统的物性差异也就越大,基质向裂缝窜流阶段的压力导数曲线特征越明显,反映基质向裂缝窜流的窜流凹子也就越深.
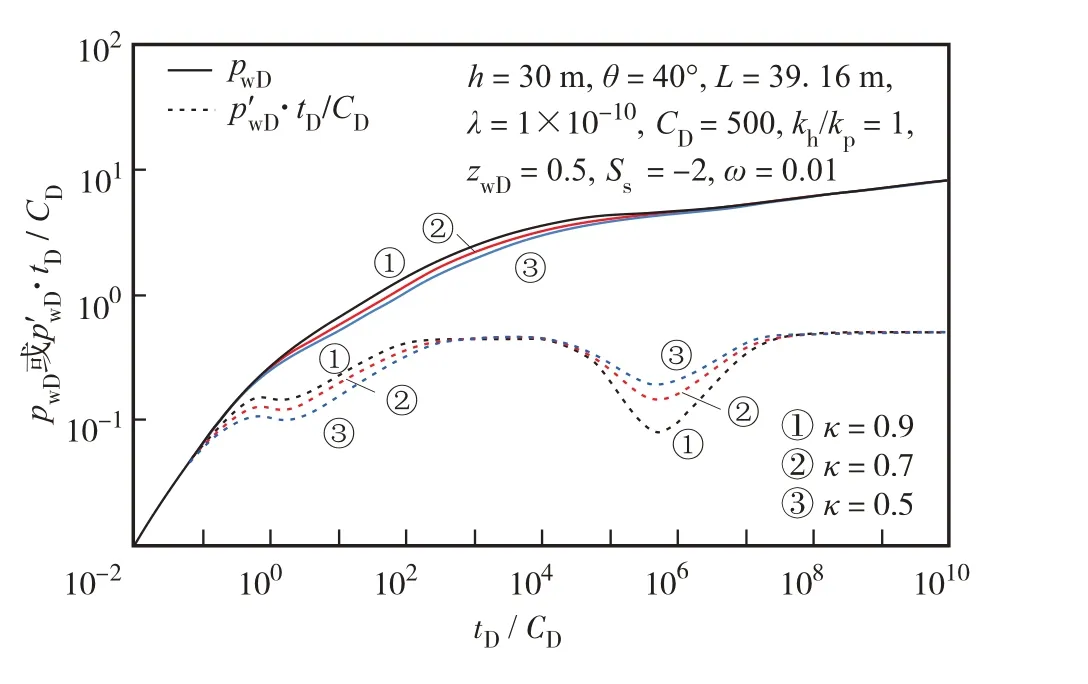
图7 裂缝与总系统渗透率比值对压力动态特征曲线的影响Fig.7(Color online)Influence of permeability ratio of fracture to total system on pressure dynamic characteristic curves.
此外,反映裂缝性双孔介质油藏特性的窜流系数λ和储容比ω对压力动态特征曲线的影响与双孔单渗模型[13]类似,此处不再赘述.
4 结论
建立了双孔双渗油藏斜井物理及数学模型,并运用拉氏变换和点源函数叠加原理等方法求得此类油藏斜井井底的压力响应,绘制了相应的压力动态特征曲线.结论如下:
1)双孔双渗油藏斜井的压力动态特征曲线存在7个流动阶段:纯井筒储集效应阶段、表皮效应阶段、早期径向流阶段、中期线性流阶段、过渡流阶段、窜流阶段和晚期整体径向流阶段.
2)直井、斜井和水平井的压力特征曲线逐次变低;与直井相比,斜井的压力导数曲线多了早期径向流阶段和中期线性流阶段;与水平井相比,斜井压力导数曲线上的早期径向流阶段和中期线性流阶段持续时间均比水平井短.
3)井斜角θ和斜井井长L主要影响压力动态特征曲线的早期径向流阶段和中期线性流阶段,井斜角越大、井长越长压力及压力导数曲线位置越低,且中期线性流持续的时间越长.
4)裂缝系统与总系统渗透率比值κ影响压力动态特征曲线的早期径向流阶段、中期线性流阶段和窜流阶段,随着κ的增大,窜流凹子越深.

