局部非热平衡对增强型地热系统的影响探究

程林松，时俊杰，曹仁义，杨晨旭，杜旭林

中国石油大学（北京）石油工程学院，北京 102249

全球碳中和进程的加速，使清洁可再生能源的地位不断提高，倒逼中国能源体系朝着能源多元化发展结构持续转型．干热岩（hot dry rock，HDR）是一种储量丰富、分布广、埋藏深的清洁地热能源，近年来受到广泛关注［1-2］．HDR的有效开发需要依托体积压裂技术构建的增强型地热系统，这就导致大量温度低于储层温度的流体进入到地层中．复杂的地下储层环境导致了复杂的流动和传热过程，精确模拟和描述致密基质-复杂裂缝传质传热过程是探究干热岩开发过程的关键．

裂缝是地下流体主要的渗流通道，研究这一问题的首要任务是精确表征复杂裂缝的分布．双重介质模型是目前商业数值模拟中广泛使用的描述裂缝性储层的传统方法［3］，赵延林等［4］建立了双重介质温度场-渗流场-应力场耦合数学模型，研究认为，变温条件下温度场对裂缝渗流场具有显著的耦合作用．WANG等［5］基于双重介质模型模拟了增强型地热系统中传质传热过程，发现冷水注入使裂缝渗透率提高了7倍．双重介质模型所需的参数较少，计算效率较高，但其假设裂缝是规则分布的，导致无法准确刻画裂缝分布形态．离散裂缝模型（discrete fracture model，DFM）能够根据裂缝几何形状准确地捕捉基质-裂缝之间的质量或热量传递，从而提供更准确的模拟结果．SUN等［6］基于离散裂缝模型和有限元方法建立了满足局部非热平衡假设的热流固（thermal-hydraulic-mechanical，THM）耦合数学模型，表明了考虑热流固耦合在增强型地热系统研究中的重要性．但DFM在计算效率和计算成本方面，仍有一定局限性．LEE等［7］首次提出嵌入式离散裂缝模型（embedded discrete fracture model，EDFM），该方法可以避免非结构网格的剖分，大幅减少网格数量，从而提高计算效率．EDFM方法已经应用到各类裂缝性油气藏模拟的各种复杂情况中．WANG等［8］利用积分有限差分法，将这种嵌入式裂缝建模方法直接应用到地热储层裂缝系统中，认为该方法在真实三维离散裂缝的传质传热问题上具有很好的应用前景．基于EDFM方法，LI等［9］提出了一种研究裂缝地热储层的流动和传热的本征正交分解降阶模型，对基质与裂缝之间的传质传热求解进行简化，使计算效率提高了10～15倍．PRADITIA等［10］在EDFM的框架下，提出了一种裂缝性油藏的单相热流耦合方程的多尺度方法．SHI等［11］针对传统EDFM方法中对基质与裂缝之间的传质传热量计算精度不足的问题，提出用局部边界元方法提高了温度场和渗流场的计算准确性．然而，目前基于EDFM方法的传热过程研究均是基于局部热平衡假设（local thermal equilibrium，LTE），尚无研究考虑局部非热平衡假设（local thermal non-equilibrium，LTNE）下的EDFM方法．

关于局部非热平衡效应对传热过程的影响已有较多研究．路朗［12］研究发现，多孔介质入口位置处局部非热平衡效应更显著．YANG等［13］讨论了在考虑局部非热平衡假设下，Darcy数和Biot数等对多孔介质-流体界面热条件的影响．曲占庆等［14］建立了基于局部非热平衡的双重介质模型，讨论裂缝分布和注采参数对于干热岩采热性能的影响，但未讨论局部非热平衡假设考虑的必要性．骆雄飞等［15］讨论了内含热源的平行平板模型换热过程中局部非热平衡模型的必要性，但主要集中在特征参数的影响上．欧阳小龙［16］用Peclet数和Stanton数作为增强型地热系统是否考虑局部非热平衡假设的判别依据，针对模型为一维有限空间而未考虑裂缝存在的情况，目前，尚无针对致密基质-复杂裂缝传热过程中局部非热平衡效应影响程度的研究，相应的储层参数对考虑局部非热平衡假设必要性的影响规律还未明确．

本研究聚焦增强型地热系统的工程背景，基于局部非热平衡假设，从微观孔喉模型和嵌入式离散裂缝模型两个层面重点探究局部非热平衡对于致密基质-复杂裂缝系统传热过程的影响．明确了压力梯度、基质孔隙度、裂缝孔隙度、基质渗透率、裂缝渗透率、对流换热系数以及热扩散系数的大小对于考虑局部非热平衡假设必要性的影响，从而为增强型地热系统的数值模拟工作提供参考．

1 耦合模型建立与求解

1.1 物理模型及控制方程

1.1.1 微观传质传热耦合模型

微观孔隙尺度的压差传质可用Navier-Stokes方程进行描述，

其中，v为流体速度矢量，单位：m/s；t为流动时间，单位：s；ρf为流体密度，单位：kg/m3；pf为流体压力，单位：Pa；μf为流体黏度，单位：Pa·s；I为单位张量；F为作用在流体上的体积力矢量，单位：N/m3；上标T表示对矩阵进行转置．

用对流扩散方程描述微观孔隙尺度下的浓度扩散过程为

其中，c为流体的浓度，单位：mol/m3；D为扩散系数，单位：m2/s，R为源汇项，单位：mol/（m3·s）．在岩石区域只考虑热传导作用，能量守恒方程为

在流体区域考虑热传导和热对流作用的能量守恒方程为

其中，下标r和f分别表示岩石和流体；Tr和Tf分别为岩石和流体的热力学温度，单位：K；ρr和ρf分别为岩石和流体的密度，单位：kg/m3；cpr和cpf分别为岩石和流体的比热，单位：J/（kg·K），λr和λf分别为岩石和流体的导热系数，单位：W/（m·K）；q为热源项，单位：W/m3．

利用COMSOL Multiphysics软件的PARDISO求解器进行传质传热过程的顺序耦合求解，其优点在于占用内存小，计算效率高．

通过扫描电镜图片提取微观孔吼结构见图1，其中，蓝色部分为流体流动通道，灰色部分为岩石骨架，2条红色虚线之间为主要的渗流通道（裂缝区域），周围为近裂缝基质区域．

图1 孔喉模型轮廓及网格划分 （a）孔喉模型及主流通道；（b）网格划分结果Fig.1 Pore-throat model outline and mesh generation.(a)Pore-throat model and mainstream channel(region between two red lines is the main seepage channel),and(b)results of grid division.

1.1.2 嵌入式离散裂缝模型

在嵌入式离散裂缝模型中，基质和裂缝被划分为两个相对独立的系统，系统之间的质量和热量传递分别表示为各自方程的源项和汇项，以基质系统为例，基于EDFM方法的质量守恒方程为

其中，下标M、F和W分别指代基质、裂缝和井；kM为基质渗透率，单位：um2；φM为基质孔隙度；V为基质网格或裂缝网格内部区域体积；dV为基质网格或裂缝网格内的体积微元；η为单位转换系数；Bf为流体体积系数．式（5）等号左边第1项为时间累计项；第2项为扩散项；等号右侧是源汇项，QMF为单位时间内流体通过基质网格和裂缝单元间传递的流体质量，单位：kg/s；QMW为单位时间内流体通过基质网格和井单元间传递的流体质量，单位：kg/s．

式（5）基于有限体积法的离散形式为

其中，下标i和j分别为相邻基质网格或裂缝单元的编号；n为相邻基质网格边数；G为几何传质系数，根据图2的4种网格连接类型对此物理量进行定义．

表1列举了不同网格连接方式下几何系数的计算公式．其中，下标g表示相交裂缝处任一裂缝单元的编号；S为网格接触面的面积，单位：m2；d为裂缝网格中心到交点或交面的距离，单位：m；Δx、Δy和Δz分别为基质网格在x、y和z方向的长度，单位：m；γ为储层厚度，单位：m；L为裂缝单元的长度，单位：m；w为裂缝宽度，单位：m；N为基质网格中包含的裂缝网格总数．

表1 不同网格连接方式下几何系数的计算公式Table 1 The calculation formula of geometric coefficient with different grid connection types

在传统EDFM方法中，对于图2中所示的第④类连接方式，通常假设在基质网格中压力沿裂缝的垂直方向线性变化，但在致密基质渗透率较低时，压力传播速度较慢，基质网格中压力分布沿垂直于裂缝方向呈线性分布的假设在模拟过程中是不合理的，特别是在生产初期存在一定的计算误差．本研究采用边界元法计算基质与裂缝之间的传递的流体质量，可大幅提高计算精度［16］，其矩阵形式为

图2 EDFM中4种网格连接类型Fig.2 Four types of grid connection in EDFM.

其中，PM为基质网格压力矩阵，PF为裂缝网格压力矩阵；K为转换矩阵；其余矩阵A、B、C、E、J和H为边界积分矩阵，其内部元素表达式请扫描论文末页右下角二维码，查看补充材料1．井单元在圆柱形储集层的中心注入或生产流体．边界条件可以考虑定流量边界或者定压边界．注采过程假定为拟稳态径向渗流．与井相关的质量源汇项为

其中，rW为井的半径，单位：m；θ为水平井与裂缝网格平面法向量的夹角，单位：（°）；re为等效供给半径，单位：m，可采用Peaceman公式［18］进行求解．式（10）表示井与基质相连，式（11）表示井与裂缝相连．

同样以基质系统为例，给出基于嵌入式离散裂缝模型的基质内流体能量守恒方程为

岩石能量守恒方程为

其中，a为岩石比表面积，单位：m-1；h为对流换热系数，单位：W/（m2·K）；Uf为流体热传导产生的源汇项，单位：W；Ur为岩石热传导产生的源汇项，单位：W．式（12）和式（13）两个能量守恒方程的有限体积离散形式分别为

其中，H为几何传热系数，计算公式见表1．

对于图2所示的第④类连接的传热计算，传统EDFM沿用与传质过程相似的线性分布假设，这同样会导致基质与裂缝之间的传导传热量计算出现误差．对传统EDFM在处理致密基质-裂缝热流耦合问题上存在的精度问题，误差一方面来源于第④类连接关系中基质网格的压力和温度沿垂直于裂缝面方向呈线性变化的假设，这会导致基质与裂缝之间的传质量和热传导传热量产生计算误差．另一方面，基质与裂缝之间的传质量又会影响基质与裂缝之间热对流传热量的计算，同时，温度场和渗流场相互耦合又会让误差不断累加．本质上需要解决的是EDFM第④类连接关系中的传质传热量的计算．为提高计算精度，本研究采用局部边界元法对热传导传热量进行求解问题［11］．以流体能量守恒方程中的基质与裂缝之间的热传导项的计算为例，其矩阵形式为

对于直井和水平井注水井，流体流入或流出基质网格，热对流源汇项为

对于压裂水平井注水井，流体流入或流出裂缝网格，热对流源汇项为

热流耦合求解通常有顺序隐式耦合和完全耦合全隐式两种耦合方法．顺序隐式耦合求解方法将整个非线性方程组分成压力部分和温度部分并依次求解，主要用于传质和传热方程之间耦合不明显的单相系统［10］．完全耦合全隐式方法是在单个牛顿迭代步内同时求解整个非线性方程组．由于流动方程和温度方程之间的强耦合作用，顺序隐式耦合方法通常会由于许多外环顺序迭代而表现不佳．因此，本研究考虑完全隐式耦合，采用牛顿迭代法隐式求解整个方程组．模型的验证请扫描论文末页右下角二维码查看补充材料2．

1.2 热流耦合机理

在地下储层的高压高温环境中，水相的黏度μf、密度ρf、导热系数λf和比热容cpf不再恒定，这将极大地改变流体的质量和能量传递过程．通过式（19）—式（22）［19-20］计算水相的相关物理量．

2 LTE和LTNE模拟结果对比

2.1 微观传质传热模拟结果

微观传质传热模型仿真模拟参数见表2．

表2 微观传质传热模型主要物理量及取值Table 2 Values of main physical quantities of the microscopic mass and heat transfer model

图3为t=0.01 s时考虑局部热平衡假设和局部非热平衡假设下流体和岩石的温度分布．其中，从图3（a）和（b）的局部热平衡假设模拟结果可见，流体与接触岩石表面温度相同，即流体流过岩石表面的瞬间达到了热平衡状态，体现为岩石颗粒在较短的时间内被冷却．图3（c）和（d）为与局部热平衡假设相同模拟条件下，考虑局部非热平衡假设时的模拟结果，可以看到流体与接触岩石表面温度并不相同，流体的冷却速度较局部热平衡假设更快，而岩石颗粒冷却过程更慢，原因是岩石向流体传递的能量变少．

图3 t=0.01 s时的温度分布（a）LTE流体温度场；（b）LTE岩石温度场；（c）LTNE流体温度场；（d）LTNE岩石温度场Fig.3 Temperature distribution(t=0.01 s).(a)Fluid temperature field(LTE),(b)rock temperature field(LTE),(c)fluid temperature field(LTNE),and(d)rock temperature field(LTNE).

通过对比上述两个案例的温度分布情况，可以看出局部热平衡假设低估了在入口处和近裂缝区域的岩石温度，而高估了传热前缘区域的流体温度．

2.2 复杂裂缝模型模拟结果

通过一个多裂缝传质传热模型（图4）研究复杂裂缝条件下的局部非热平衡假设的影响．模型大小为100 m×100 m×10 m，流体黏度、密度、导热系数和比热随温度变化，原始地层温度为180℃，在模型左侧模拟水平井定压30 MPa注入，在模型右侧模拟水平井定压10 MPa采出．其余主要的模拟参数见表3．

表3 复杂裂缝模型主要参数及取值Table 3 Main parameters and values of the complex fracture model

图4 复杂裂缝模型示意图Fig.4 Schematic diagram of complex fracture model.Red line is the injection end,light blue line is the produced end,and blue lines are the fractures.

模拟结果如图5，在局部非热平衡假设下，岩石和流体的温度分布之间长时间尺度上的差别不大，而局部热平衡模型和局部非热平衡模型之间存在较大差异，局部热平衡实际上高估了产出流体温度，这对于增强型地热系统来说，可能会导致系统的生命周期被高估，从而带来经济上的损失．因此，局部非热平衡模型中岩石和流体温度之间的微小差异，不一定会导致局部热平衡模型和局部非热平衡模型之间的温度差异小，有必要对局部非热平衡模型的适用性和敏感性进一步研究．

图5 局部热平衡和局部非热平衡条件下的温度场（t=1000 d）（a）LTE温度场；（b）LTNE流体温度场；（c）LTNE岩石温度场Fig.5 Schematic diagram of multi-fracture model(t=1000 d).(a)LTE temperature field,(b)LTNE fluid temperature field,and(c)LTNE rock temperature field.

3 参数敏感性分析

3.1 微观孔喉模型参数敏感性

图6为不同压力梯度下流体和岩石在局部热平衡和局部非热平衡假设条件下的温度场分布．由图6可见，局部热平衡假设比局部非热平衡假设流体冷却岩石的速度要快．对比来看，局部热平衡假设会高估产出流体的温度，低估岩石的温度，且压力梯度越小，局部非热平衡效应越不明显．这是因为压力梯度越小，流体流动速度越慢，使得流体和岩石有更多的时间进行对流换热，从而使接触面上的温度达到平衡．

图6 t=0.01 s时不同压力梯度下岩石和流体温度分布（a）和（b）分别为1.0 MPa/m时LTE和LTNE岩石温度场；（c）和（d）分别为1.0 MPa/m时LTE和LTNE流体温度场；（e）和（f）分别为0.5 MPa/m时LTE和LTNE岩石温度场；（g）和（h）分别为0.5 MPa/m时LTE和LTNE流体温度场；（i）和（j）分别为0.2 MPa/m时LTE和LTNE岩石温度场；（k）和（l）分别为0.2 MPa/m时LTE和LTNE流体温度场Fig.6 Temperature distribution of fluid and rock with different pressure gradients(t=0.01 s).(a)1.0 MPa/m,LTE,rock temperature distribution,(b)1.0 MPa/m,LTNE,rock temperature distribution,(c)1.0 MPa/m,LTE,fluid temperature distribution,(d)1.0 MPa/m,LTNE,fluid temperature distribution,(e)0.5 MPa/m,LTE,rock temperature distribution,(f)0.5 MPa/m,LTNE,rock temperature distribution,(g)0.5 MPa/m,LTE,fluid temperature distribution,(h)0.5 MPa/m,LTNE,fluid temperature distribution,(i)0.2 MPa/m,LTE,rock temperature distribution,(j)0.2 MPa/m,LTNE,rock temperature distribution,(k)0.2 MPa/m,LTE,fluid temperature distribution,and(l)0.2 MPa/m,LTNE,fluid temperature distribution.

由于对流换热系数h在实际中往往难以准确测定，本研究对比了不同对流换热系数下的局部非热平衡效应．图7为不同对流换热系数下的温度场分布．对比局部热平衡结果可以看出，当h较小时，局部热非平衡效应影响较大，随着h的增大，两种假设的温度场逐渐趋于相似．

图7 局部热平衡假设与局部非热平衡假设不同对流换热系数下温度场（t=0.01 s）（a）LTE；（b）h=5×103 W/(m2·K)；（c）h=1×104 W/(m2·K)；（d）h=2×104 W/(m2·K)Fig.7 Comparison of different surface heat transfer coefficient and local thermal equilibrium temperature field(t=0.01 s).(a)LTE,(b)h=5×103 W/(m2·K),(c)h=1×104 W/(m2·K),and(d)h=2×104 W/(m2·K).

3.2 复杂裂缝模型参数敏感性

针对复杂裂缝模型，基于EDFM方法对不同储层参数的局部非热平衡效应大小及随时间变化规律进行分析．模型的基础参数如下：基质孔隙度为0.1，基质渗透率为2×10-4μm2，裂缝孔隙度为0.2，裂缝渗透率为20 μm2，岩石导热系数为3 W/（m·K），岩石比热为850 J/（kg·K），岩石密度为2.6×103kg/m3，ah=500 W/（m3·K），在此基础上通过控制单一变量进行研究．定义一个流体平均温度误差值（由式（23）计算）量化整个基质裂缝区域局部非热平衡效应的大小，该值越大表示局部热平衡假设对基质和裂缝平均流体温度的高估程度越大．

3.2.1 不同基质孔隙度和裂缝孔隙度的影响

图8和图9分别为不同基质孔隙度和不同裂缝孔隙度相对误差．从图8和图9可见，局部热平衡假设对储层中流体温度场的高估幅度先上升后下降，原因是低温区是逐渐波及又趋于稳定的，最终区域内岩石温度降低至注入流体温度．同时可以看到，基质孔隙度越小，局部非热平衡假设的影响越显著．裂缝孔隙度越高，局部非热平衡假设的影响越显著．可以推断，当基质孔隙度和裂缝孔隙度差别越大，越需要考虑局部非热平衡假设．总体而言，孔隙度对局部非热平衡效应影响较大，原因是在LTE模型中，孔隙度影响了体积平均参数的大小，比如岩石流体的平均密度、平均比热和平均导热系数，而由式（12）和式（13）可知，在LTNE模型中，孔隙度对岩石及流体热量的传递均有影响．

图8 不同基质孔隙度相对误差Fig.8 Relative errors of different matrix porosity.

图9 不同裂缝孔隙度相对误差Fig.9 The relative errors of different fracture porosity.

3.2.2 不同基质渗透率和裂缝渗透率的影响

图10和图11分别为不同基质渗透率和不同裂缝渗透率相对误差．从图10和图11可见，两种模型计算结果的误差最大值随基质渗透率和裂缝渗透率的降低而增加．从时间尺度上总体来看，随着基质渗透率和裂缝渗透率的增大，早期局部非热平衡效应越显著，但在中后期，基质渗透率和裂缝渗透率越低局部非热平衡效应越显著，这是由于随着渗透率的增大，渗流速度增大导致的热对流作用增强，使得岩石被冷却的速度越快，在早期，流速越快岩石和流体换热越不充分导致两者差异越大，而随着时间推移，两种模型计算结果的差异性逐渐变小，且局部非热平衡效应对基质渗透率的敏感程度大于裂缝渗透率．

图10 不同基质渗透率相对误差Fig.10 Relative errors of porosity of different matrix.

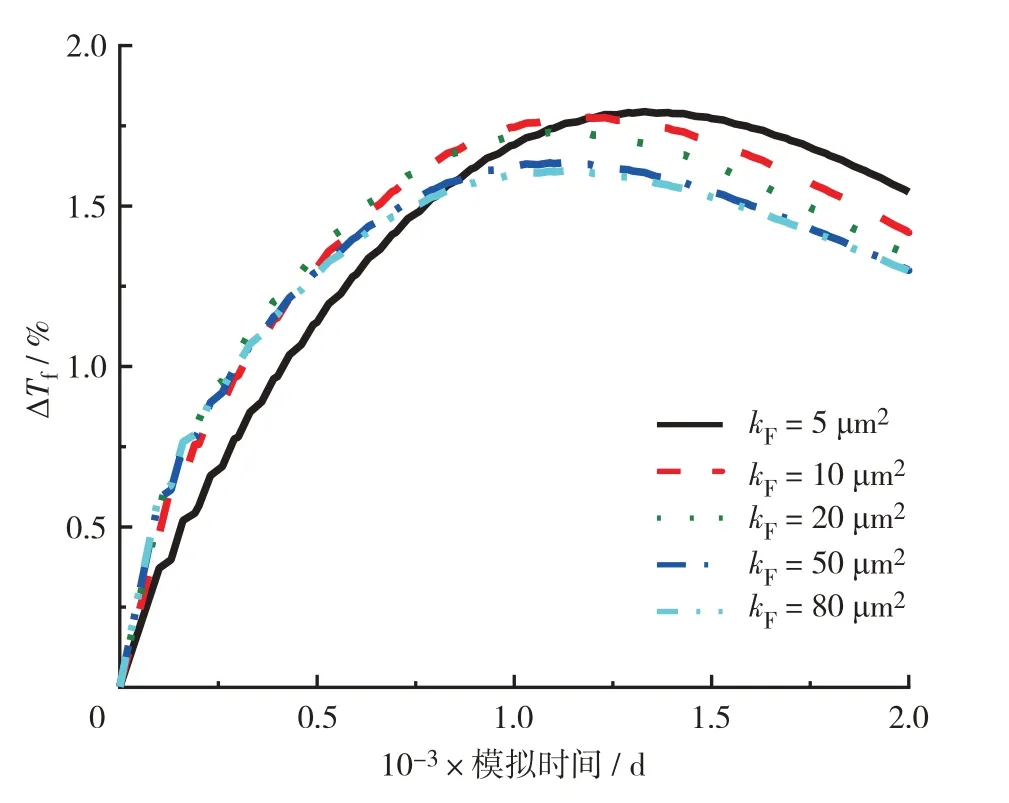
图11 不同裂缝渗透率相对误差Fig.11 The relative errors of different fracture porosity.

3.2.3 不同热扩散系数和对流换热系数的影响

从不同热扩数系数相对误差（图12）和不同对流换热系数相对误差（图13）可以看出，岩石热扩散系数(α=λr/(cpr·ρr))越大，局部非热平衡效应越显著．对流换热系数越小，局部非热平衡效应越显著，这是由于对流换热系数越小，岩石表面与流体的换热能力越差．因此，当岩石的热扩散系数较大或对流换热系数较小时，需要考虑局部非热平衡模型．

图12 不同热扩散系数相对误差Fig.12 Relative errors of different thermal diffusivity matrix.

图13 不同对流换热系数相对误差Fig.13 Relative errors of different convective heat transfer coefficient.

4 结论

考虑局部非热平衡假设，建立了基于有限元方法的微观传质传热的毫米尺度数值实验模型，和基于局部边界元和有限体积方法的宏观嵌入式离散裂缝传质传热模型，形成了致密基质-复杂缝网传质传热数值模拟方法，并分析了局部非热平衡假设对传热过程的影响．研究可知：

1）所提出的改进EDFM方法可以有效模拟考虑局部非热平衡假设的致密基质-复杂裂缝的传质传热过程，考虑局部非热平衡假设能提高基质-裂缝传质传热过程模拟的准确性；

2）局部热平衡假设会低估入口处和近裂缝区域的岩石温度，而高估传热前缘区域的流体温度；

3）局部非热平衡对增强型地热系统的影响主要体现在注入早期，而注入强度越高、或基质裂缝渗透率越低、或基质裂缝孔隙度差异越大、或岩石热扩散系数越大、或对流换热系数越小，都越需要考虑局部非热平衡假设.

事实上，影响对流传热过程的诸多因素均体现在对流换热系数的确定上，模型中将其考虑成常数存在局限性，未来工作中需进一步探究．