基于ONERA模型的柔性叶片气弹稳定性研究
李治国,陈 猛,张雅静,高志鹰,汪建文
(1.内蒙古工业大学 机械工程学院,内蒙古 呼和浩特 010051;2.内蒙古工业大学 能源与动力工程学院,内蒙古 呼和浩特 010051;3.内蒙古建筑职业技术学院 交通与市政工程学院,内蒙古 呼和浩特 010070;4.内蒙古工业大学 风能太阳能利用技术教育部重点实验室,内蒙古 呼和浩特 010051)
0 引言
风力机叶片气动弹性问题大多是挥舞、摆振以及扭转之间的耦合,可形成破坏力极强的经典颤振,是叶片设计时必须考虑的重点问题[1]。当前风力机逐渐向大型化发展,叶片越发细长,抗弯曲能力逐渐减弱,使叶片容易弯折破坏[2]。由于叶片扭转刚度较大并且气动力产生的扭矩较小,所以挥舞变形与摆振变形是叶片容易弯折破坏的主要因素。研究柔性叶片气弹稳定性对保护叶片,防止叶片的弯折破坏尤为重要。
文献[3]~[5]基于ONERA气动力模型对翼型的动态失速进行了研究,计算出了失速翼型的颤振临界速度,得到了气动力模型的适用范围和在深失速等具有明显多级失速现象下的计算精度。文献[6]~[8]利用ONERA非定常气动力模型,对翼型进行非线性气动弹性分析,研究非定常气动力对翼型的影响并建立了非定常气弹动力学模型。常林[9]模拟了极端条件下叶片的挥舞和摆振方向受迫振动。Chaviaropoulos P K[10]基于常值变桨角和典型截面,研究了挥舞-扭转、挥舞-摆振的颤振问题。杨浩南[11]采用修正动量叶素理论(BEM)和几何精确梁理论(GEBT)耦合的叶片气弹研究方法,研究了不同来流条件下叶片和塔筒的气弹变形及其对风力机气动性能和载荷的影响。黄鑫祥[12]基于风力机整机刚柔耦合模型,提出了一种叶片动态气弹扭转变形分析的新方法,并分析叶片气弹扭转变形对风力机气动功率及气弹稳定性的影响。
研究人员已从不同角度对叶片气弹稳定性问题进行了研究,但对叶片变桨前后的气弹稳定性研究相对较少。为了探究大型风力机柔性叶片在挥舞-摆振耦合作用下变桨前后的气弹稳定性,本文基于ONERA非线性气动模型建立包括二维翼型非线性气动升阻力方程及其挥舞-摆振耦合的简化运动方程的气弹模型。利用该模型计算美国国家能源实验室(NREL)5 MW风力机叶片中段的DU35-A17翼型变桨前后挥舞、摆振变形量,并与开源软件FAST计算得到的结果进行对比分析,验证本文建立的气弹稳定模型的正确性。
1 叶片气弹方程
1.1 柔性叶片挥舞-摆振耦合运动方程
ONERA模型以微分方程组的形式给出了气动载荷的表达式[13]。旋转叶片挥舞-摆振耦合的简化运动方程为[14]


图1所示为风力机叶片截面结构与坐标系示意图。图中,α为攻角,θ为扭角,θ0为桨距角,φ为相对风速角,U为风速,V为相对风速,Ω为叶片旋转角速度,r为旋转半径。

图1 风力机叶片截面坐标示意图Fig.1 Cross section coordinate diagram of wind turbine
1.2 ONERA气动力模型
本文采用ONERA非线性气动力模型[15]。
1.2.1 非线性升力系数
通过式(2)得到叶片截面的非线性升力系数。

式中:CLa为线性气动力部分对应的与升力有关的气动力系数;CLb为非线性气动力部分对应的与升力有关的气动力系数;(')为关于时间或攻角的一阶导数;(″)为关于时间或攻角的二阶导数;CLy为与升力有关的空气动力系数;ΔCL为静态空气动力系数曲线线性部分的延长线与曲线非线性部分的差;SZ1,SZ2,SZ3,α0z,λ1,λ2均为与线性气动力部分有关的参数;r1z,r2z,r3z均为与雷诺数有关的参数。
ONERA模型中的线性部分是对经典的Theodorsen气动力的模拟,因此,ONERA模型中与线性气动力部分有关的参数SZ1,SZ2,SZ3,α0z,λ1,λ2便可以依据两者之间的关系确定[16]。参数值分别为SZ1=π,SZ2=π/2,SZ3=0,α0z=5.9,λ1=0.15,λ2=0.55。
为了方便计算,通常将静态气动力曲线简化为折线的形式(图2)。

图2 静态气动力曲线简化图Fig.2 Simplified diagram of static aerodynamic curve

由图2可以近似得到ΔCL的表达式。
1.2.2 非线性阻力系数
通过下式可以计算出叶片截面的阻力系数。
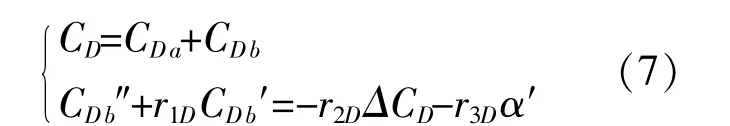
式中:CDa,CDb为阻力系数的组成部分;ΔCD为线性部分阻力系数与非线性部分阻力系数的差值;r1D,r2D,r3D均为与阻力系数有关的参数。
式中各参数的值为

最后通过将上述公式联立解微分方程组即可求出叶片的挥舞、摆振变形量。本文选用四阶龙格-库塔法计算微分方程组。

式中:设X1为z;X2为z';X3为y;X4为y';X5为CLy;X6为CLb;X7为CLb';X8为CDb;X9为CDb'。
ONERA气动力模型计算流程如图3所示。

图3 ONERA气动力模型计算流程图Fig.3 Calculation flow chart of ONERA aerodynamic model
2 算例分析
本文选用NREL 5 MW风力机叶片中的Du35-A17翼型进行计算,此翼型弦长为4.652 m,扭角为11.48°,截面的旋转半径r为15.85 m,额定风速为11.4 m/s。风力机风速与桨距角变化关系见表1。

表1 不同风速下风力机桨距角Table 1 Pitch angle of the wind turbine under different wind speeds
2.1 气弹模型验证
为了验证本文气弹模型的准确性,对NREL 5 MW风力机在额定工况下的叶尖变形量进行计算并与NREL的FAST软件进行对比,两种方法计算结果如图4所示。
由图4可知:FAST计算的挥舞变形量为5.945 8 m,摆振变形量为-1.108 3×10-1~-1.528 7×10-1m,均值为-6.305 7×10-1m;ONERA模型计算的舞变形量为5.923 0 m,较FAST计算结果小0.383 5%,摆振变形量为-1.044 6×10-1~-2.802 6×10-1m,均值为-6.624 3×10-1m,较FAST计算结果大5.0526%。ONERA模型计算结果稳定后与FAST计算结果基本吻合,可以认为本文模型能够用于分析叶片气弹稳定性。

图4 额定工况下两种方式计算的叶尖变形量Fig.4 Calculation of tip deflection in two ways under rated working conditions
2.2 未变桨时叶片挥舞摆振变形量
利用ONERA模型对叶片运动进行分析,分别计算了当风速为5,8 m/s和10 m/s时叶片中段(r=15.85 m)的挥舞变形量与摆振变形量。此3种风速皆在风力机的设计工作范围内,所以挥舞变形量与摆振变形量均是收敛的。图5,6分别为未变桨时挥舞变形图和摆振变形图。

图5 未变桨时挥舞变形图Fig.5 Flapwise deflection without pitching

图6 未变桨时摆振变形图Fig.6 Edgewise deflection without pitching
由图5,6可知:挥舞变形量最终会收敛为一个固定值,摆振变形量则稳定在一个范围内作规律的变化;当风速为5 m/s时,叶片的挥舞变形量最终稳定在2.834×10-2m,摆振变形量稳定在-2.788×10-3~-2.312×10-3m;当风速为8 m/s时,叶片的挥舞变形量最终会稳定在4.72×10-2m,摆振变形量稳定在-7.089×10-3~-6.190×10-3m;当风速为10 m/s时,叶片的挥舞变形量最终会稳定在5.108×10-2m,摆振变形量稳定在-8.185×10-3~-7.157×10-3m。
随着风速的增大,叶片的挥舞与摆振方向的变形明显增大。这是由于风力机未变桨,在叶片z向、y向抗弯刚度相同的情况下,随着风速的增加,叶片表面所受风载荷增加,使得叶片的变形量增大。相较于风速为5 m/s时,风速为10 m/s时的挥舞变形量增加近一倍,摆振变形量增加近两倍。这是由于风速增加一倍,叶片所受的风载荷相应的增加一倍,挥舞变形量主要受风载荷的影响,所以增加近一倍,而摆振变形量不仅受风载荷的影响,还受叶片旋转的影响,风轮的转速会随着风速加快而加快,所以摆振变形量增加近两倍。
2.3 变桨后叶片挥舞摆振变形量
通过查找NREL 5 MW风力机手册可知,风力机的额定风速为11.4 m/s,额定转速为12.1 r/min,当风速为13 m/s时,叶片桨距角为6.60°,当风速为15 m/s时,叶片桨距角为10.45°。利用ONERA模型对叶片运动进行分析,分别计算当风速为11.4,13 m/s和15 m/s时叶片的挥舞变形量与摆振变形量。由于叶片的变桨,此3种风速仍在风力机的设计工作范围内,所以挥舞变形量与摆振变形量均是收敛的。图7,8分别为叶片变桨后挥舞变形图和摆振变形图。
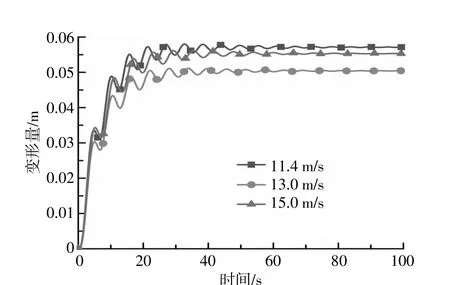
图7 变桨后挥舞变形图Fig.7 Flapwise deflection after pitching

图8 变桨后摆振变形图Fig.8 Edgewise deflection after pitching
由图7,8可知:挥舞变形量最终会收敛为一个固定值,摆振变形量最终会稳定在一个范围内作规律的变化;当风速为11.4 m/s时,叶片的挥舞变形量最终稳定在5.702×10-2m,摆振变形量稳定在-1.006×10-2~-8.800×10-3m;当风速为13 m/s时,叶片的挥舞变形量最终会稳定在5.035×10-2m,摆振变形量稳定在-7.195×10-3~-6.198×10-3m;当风速为15 m/s时,叶片的挥舞变形量最终会稳定在5.537×10-2m,摆振变形量稳定在-7.905×10-3~-6.763×10-3m。当风力机变桨之后,叶片的挥舞、摆振变形量比额定风速时的挥舞摆振变形量有所减小,这是由于随着风速的增加,风力机要维持在额定功率下运动需要变桨,增大桨距角,桨距角的增大会改变叶片的抗弯刚度,叶片抵抗变形的能力增大,使得挥舞变形量与摆振变形量相对于变桨之前有所下降。而随着风速从13~15 m/s的进一步增大,叶片继续变桨,桨距角增大,叶片所受风载荷的影响超过抗弯刚度增大的影响,叶片挥舞变形量与摆振变形量会继续随风速的增大而增大。
表2为叶片挥舞、摆振变形量计算结果。

表2 挥舞、摆振变形量计算结果Table 2 Calculation results of flapwise and edgewise deflection
3 结论
本文基于ONERA非线性气动模型,建立了包括二维翼型非线性气动升阻力方程及其挥舞-摆振耦合运动方程的柔性叶片气弹模型,计算并获得叶片中段变桨前后的挥舞、摆振变形量变化曲线,得到了风力机叶片在未变桨与变桨后,随着风速的增大,挥舞、摆振变形量的变化规律。
①在额定工况时,叶片通过向z轴正方向、y轴负方向的弯曲以抵消风载荷对叶片的影响。挥舞变形量逐渐增大到一定值后,最终会稳定在5.702×10-2m,摆振位移逐渐增大,最终会稳定在-1.006×10-2~-8.800×10-3m。
②风力机未变桨时,由于叶片抗弯刚度相同,挥舞、摆振变形量会随风速增大而增大,其中在风载荷增加一倍的情况下,挥舞变形量会随之增加近一倍达到2.274×10-2m,摆振变形量由于风载荷与叶片旋转的共同作用增加约两倍达到5.121×10-3m。
③叶片变桨后,由于叶片抗弯刚度的增加,挥舞、摆振变形量比额定工况下的变形量有所减少。随着来流风速增加,风载荷的影响超过抗弯刚度增大的影响,叶片挥舞变形量与摆振变形量会继续随风速的增大而增大。不同风速下的挥舞、摆振变形量总是收敛于某一个固定值,故叶片是气弹稳定的。

