风力发电机液压变桨系统的建模与仿真

杨红全

上海电气风电集团股份有限公司 上海 200241

1 研究背景

二十世纪七十年代初,由于石油危机导致能源紧张问题,风能作为可再生、无污染自然能源引起了人们的高度重视。近年来,世界各国均出台了一系列促进新能源发展的措施。与此同时,科学技术不断进步,风力发电的成本迅速下降,成为新能源大力崛起的重要推动力。我国的风能资源相对丰富,除西藏和新疆外,海上可开发的风能容量为7.5×108kW。风能密度高于300 W/m2和高于400 W/m2的地区,面积共有650 000 km2和280 000 km2,可以安装的发电机容量分别为3.7×109kW和2.8×109kW[1-3]。截至2017年第三季度末,我国风力发电量占各种能源发电总量的9%,位于火力发电与水力发电之后,排名第三位[4]。目前,风力发电机已向大功率、海上及陆上低速大叶片型等方向发展。风力发电机分为直驱风力发电机、半直驱风力发电机和双馈风力发电机,目前市场上以双馈风力发电机为主。双馈风力发电机需要由齿轮箱增速后进行发电[5]。桨距的控制方法有液压桨距控制、电动桨距控制和电液桨距控制[6]。液压变桨具有大功率、大扭矩、动态响应快,以及机组紧急停机后重启迅速等优势,在大功率机型中应用越来越成熟。液压变桨及控制程序比较复杂[7],液压变桨控制系统一般由国外供应商提供。可见,研究液压变桨控制技术及实现大功率风力发电机液压变桨系统国产化是当前需要解决的问题。

笔者建立风力发电机液压变桨系统数学模型,将比例阀、液压缸等参数代入数学模型,应用Matlab/Simulink软件进行仿真,验证液压变桨系统的稳定性及响应性能。液压变桨系统有多种工况,包括正常开桨、正常顺桨、快速顺桨、紧急变桨等。快速顺桨工况相比正常开桨、正常顺桨工况,控制能力较弱,笔者基于快速顺桨工况研究液压变桨系统是否合理。

2 液压变桨系统控制流程

风力发电机液压变桨系统是一种用电液比例阀控制液压缸的位置反馈系统。控制器根据风速、叶片桨距角及参考指令来控制电压,通过独立比例放大器将电压信号转换为电流信号后用于驱动电液比例阀阀芯,进而控制液压油流量和变桨油缸的方向,这一系列控制动作会使叶片桨距角在0°～90°之间变动。变桨油缸内装有位移传感器,在变桨过程中,位移传感器能根据检测到的油缸活塞杆伸出位置换算出风力发电机的叶片桨距角。液压变桨系统控制流程如图1所示。

图1 液压变桨系统控制流程

3 快速顺桨原理

风力发电机液压变桨系统执行快速顺桨动作时,液压工作原理如图2所示。来自液压站的一部分压力油经过电磁换向阀6、节流阀2、截止阀4,到达变桨锁定缸有杆腔,克服变桨锁定缸无杆腔的弹簧力,使活塞杆收缩,打开与变桨锁定缸相连接的锁定销,此时风力发电机叶片具备可以旋转的条件。与此同时,比例换向阀b端,以及电磁换向阀1、2、4同时得电,来自液压站的另一部分压力油经过单向阀3、电磁换向阀4、比例换向阀b端、电磁换向阀1、截止阀1,到达变桨油缸1、2的无杆腔,有杆腔油液经过截止阀2、单向阀2,回到进油管道,形成差动油路。此时,变桨油缸1、2的活塞杆快速伸出,风力发电机液压变桨系统完成快速顺桨动作。

4 液压变桨系统数学模型

来自液压站的压力油经过比例换向阀等元件后,到达变桨油缸,通过变桨油缸的活塞杆伸缩来完成变桨动作。风力发电机液压变桨系统有多种工况,笔者基于快速顺桨工况进行数字建模。

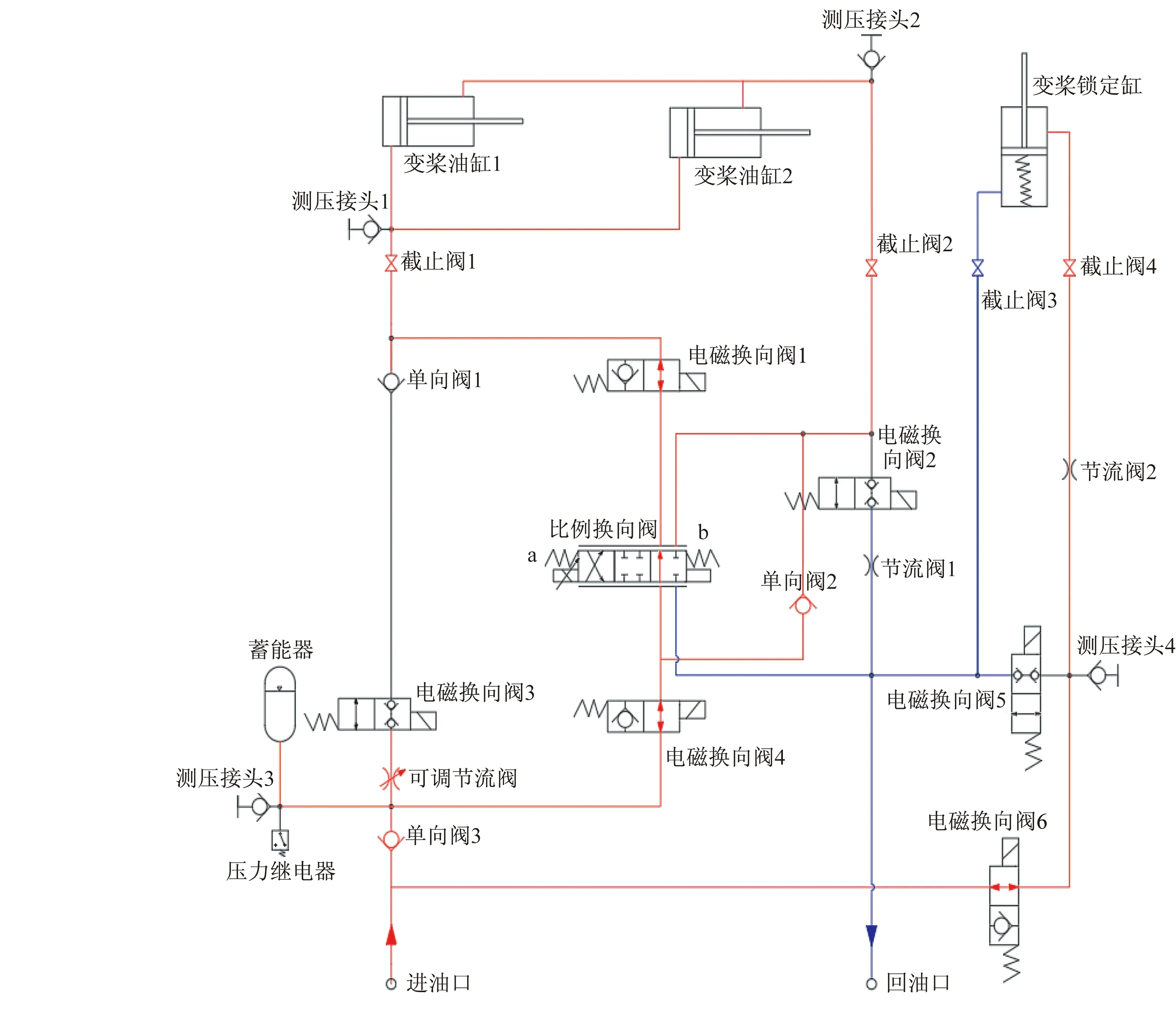
图2 快速顺桨液压工作原理

4.1 快速顺桨工况

当风力发电机液压变桨系统快速顺桨时,变桨油缸有杆腔的油通过截止阀2、单向阀2回到进油管道,此时液压系统整个回路形成差动连接,可以简化为三通阀控非对称液压缸回路,如图3所示。图3中:A1为变桨油缸无杆腔活塞的面积,m2;A2为变桨油缸有杆腔的有效作用面积,m2;Ci为油缸内泄漏系数,m2/(N·s);Ps为比例阀前油压力,Pa;P1为油缸无杆腔压力,Pa;Xv为比例阀阀芯位移,m;Xc为油缸活塞杆位移,m;Ma为叶片及油缸活塞的总质量,kg;FL为作用在活塞杆上的外负载力,N;BP为总黏性负载系数,N·s/m。

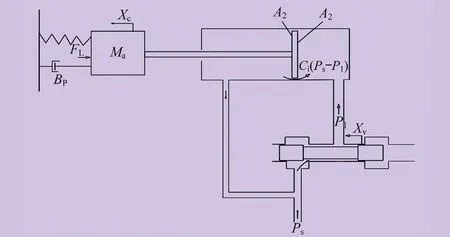
图3 三通阀控非对称液压缸回路

由三通滑阀流量公式[8]可知,在恒压源供油时,控制滑阀的负载流量QL可以表示为油缸无杆腔压力P1和阀芯位移Xv的函数。基于线性系统对液压变桨系统进行分析,得出三通阀的线性化流量方程为:

QL=KqXv-KpP1

(1)

式中:Kq为比例阀在临近稳定工作点时的流量增益,m2/s;Kp为比例阀在临近稳定工作点时的流量压力系数,m5/(N·s)。

变桨油缸无杆腔的流量连续性方程为:

(2)

式中:V1为无杆腔容积,m3;βe为液压油体积模量,N/m2。

变桨油缸的力平衡方程为:

(3)

式中:K为弹性负载,N/m。

对式(1)、式(2)、式(3)进行拉普拉斯变换,得:

QL(s)=KqXv(s)-KpP1(s)

(4)

QL=CiP1+V1sP1/βe+A1sXc

(5)

P1A1=MaXcs2+BPXcs+KXc+FL

(6)

式(4)为阀的流量方程式,式(5)为变桨油缸的流量方程式,式(6)为变桨油缸的力平衡方程,可得数学模型:

(7)

Kc=Kp+Ci

(8)

式中:Kc为总流量压力系数,m5/(N·s)。

式(7)即为变桨油缸活塞输出位移Xc与比例阀阀芯位移Xv、作用在活塞杆上外负载力FL之间的传递函数。

(9)

(10)

(11)

(12)

式中:Kh为液压弹簧刚度;ωh为快速顺桨时系统固有频率;ξh为快速顺桨时系统阻尼比。

由于无弹簧负载,即K为0,因此式(9)可以化简为:

(13)

式(13)是风力发电机液压变桨系统快速顺桨时变桨油缸输出位移与比例阀阀芯位移输入、作用在活塞杆上外负载力之间的传递函数。

变桨油缸输出位移与比例阀阀芯位移之间的传递函数为:

(14)

变桨油缸输出位移与作用在活塞杆上外负载力之间的传递函数为:

(15)

4.2 变桨油缸位移与叶片桨距角

变桨油缸位移与风力发电机叶片桨距角之间的关系如图4所示,γ为风力发电机变桨油缸最大开桨位置,此时叶片桨距角为0°,可以测量。β为风力发电机叶片桨距角,为可变参数。r为油缸活塞杆上销轴中心的旋转半径。LPC为风力发电机变桨油缸处于最大开桨位置时油缸两端销轴中心P点、C点之间的距离,为已知值。O点为叶片变桨旋转中心点,P点为变桨油缸底座销轴中心点,O点、P点之间距离LOP为固定值。D点为顺桨到当前位置的油缸活塞销轴中心点位置。

由图4可得油缸位移Xc为:

Xc=LPD-LPC

(16)

式中:LPD为P点、D点之间的距离。

图4 变桨油缸位移与叶片桨距角关系

由余弦定理得:

(17)

将式(17)代入式(16),得:

(18)

式(18)中,变桨油缸位移与叶片桨距角为非线性关系,在计算时需要进行线性化处理。

实际上,叶片桨距角β只在0°～90°范围内变化,所以在工程案例中,运用式(18)及真实数据,可以得出变桨油缸位移与叶片桨距角的关系曲线,如图5所示。

图5 变桨油缸位移与叶片桨距角关系曲线

由图5可以得出,风力发电机叶片桨距角与变桨油缸位移之间呈近似线性关系,为:

β=yXc

(19)

也可以改写为:

Xc=zβ

(20)

通过取值拟合,可得y近似值为2.13,则z为0.47 m/rad。线性化处理时,QL等于KqXv,则将式(20)代入式(14)、式(15),得:

(21)

(22)

式(21)为风力发电机液压变桨系统快速顺桨时,叶片桨距角与负载流量之间的传递函数。式(22)为风力发电机液压变桨系统快速顺桨时,叶片桨距角与作用在活塞杆上外负载力之间的传递函数。

4.3 数字控制器

数字控制器的作用是反馈变桨油缸的位置信号,与给定信号进行对比,目标是缩小偏差量。控制量经过数字模拟转换,转换为电压量,传递至比例放大器,转换为电流量,进而控制电液比例阀的阀芯位移。

4.4 比例放大器

比例放大器将电压信号放大后变换为电流信号,输送至电液比例阀。因为转折频率比固有频率高得多,所以此处可以视作线性关系,为:

I=UKa

(23)

式中:I为比例放大器输入电流,A;U为电压,V;Ka为比例放大器放大系数,A/V,此处取0.01 A/V。

4.5 电液比例阀

通常将电液比例阀视为一个二阶环节,因此电液比例阀阀芯位移与电流之间的传递函数为:

(24)

式中:Kv为电液比例阀流量增量,m3/(s·A);ωv为电液比例阀固有频率,rad/s;ξv为电液比例阀阻尼比。

4.6 位移传感器

位移传感器探测变桨油缸活塞杆的位移,转换为电压信号Uc:

Uc=XcKm

(25)

式中:Km为位移传感器增益系数,V/m。

4.7 主要性能参数

液压变桨系统元件的主要性能参数见表1。

表1 液压变桨系统元件主要性能参数

4.8 传递函数小结

由式(24)及给定的值,可得电液比例阀的传递函数为:

(26)

风力发电机液压变桨系统快速顺桨时,变桨油缸叶片桨距角与负载流量之间的传递函数为:

(27)

风力发电机液压变桨系统快速顺桨时,变桨油缸叶片桨距角与作用在活塞杆上外负载力之间的传递函数为:

(28)

4.9 传递方框图

风力发电机液压变桨系统快速顺桨时,液压变桨系统传递方框图如图6所示。

4.10 开环传递函数

由图6可得风力发电机液压变桨系统快速顺桨时,液压变桨系统开环传递函数为:

(29)

图6 液压变桨系统传递方框图

5 稳定性和响应性能分析

如图7所示,可以通过对快速顺桨时的风力发电机液压变桨系统进行频率特性分析,来了解液压变桨系统的稳定性。

液压变桨系统稳定的条件是相位裕量和增益裕量均为正值。由图7可见,相位裕量为88.6°,增益裕量为16.6 dB。根据判定条件,所研究的液压变桨系统稳定。

6 比例积分微分(PID)控制

在Matlab/Simulink软件中创建快速顺桨时风力发电机液压变桨系统的控制模型,如图8所示。

控制模型运行后,得到阶跃响应,如图9所示。

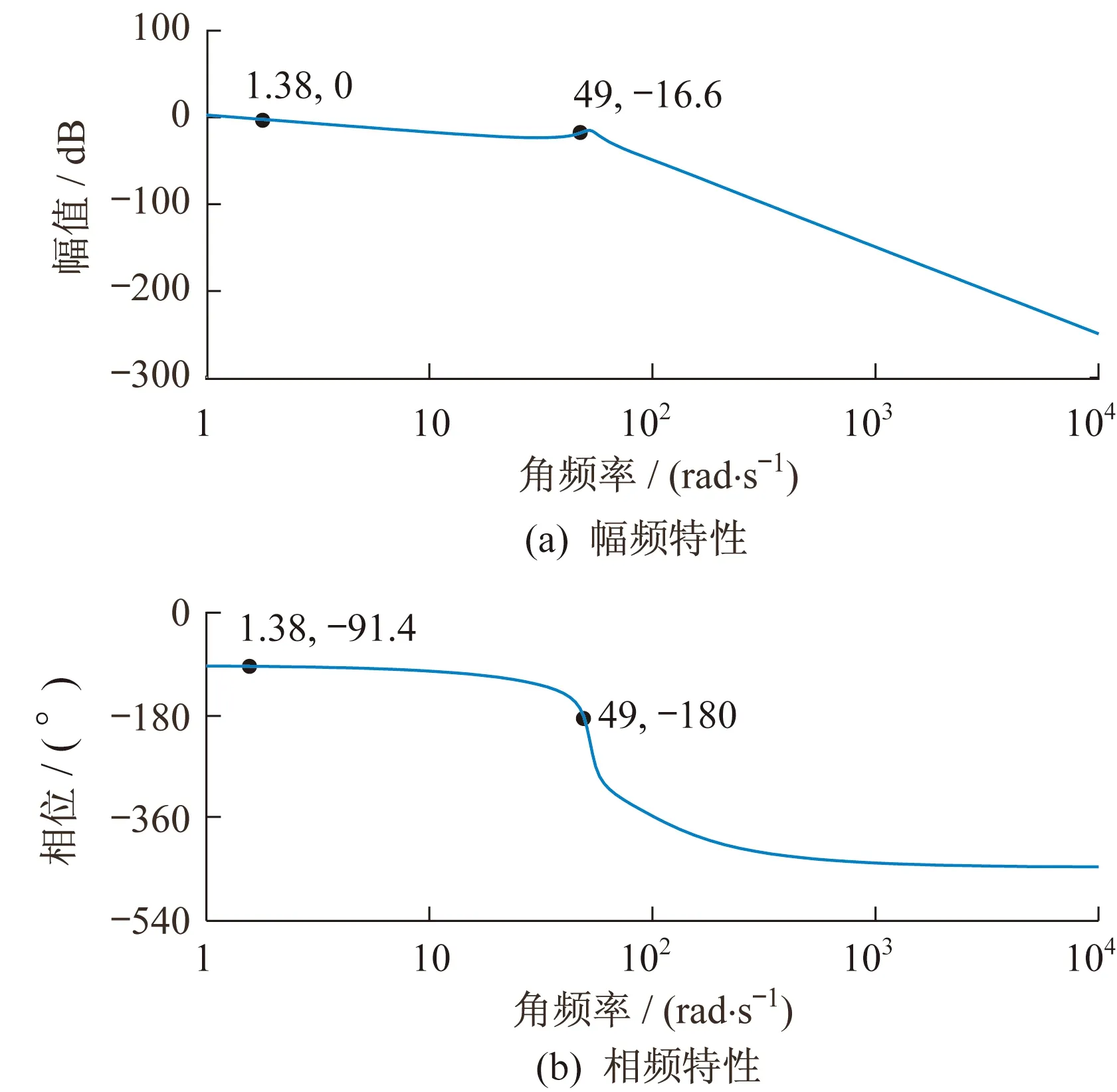
图7 液压变桨系统频率特性

图8 液压变桨系统控制模型

图9 液压变桨系统控制模型阶跃响应

在整定前,快速顺桨时风力发电机液压变桨系统的响应时间为4 s,这一响应时间偏长。在实际工程应用中,风速是瞬息万变的,所以要求响应时间短。利用PID整定后,可以缩短响应时间。

在Matlab/Simulink软件中创建风力发电机液压变桨系统PID控制模型,如图10所示。PID控制模型运行后,得到阶跃响应,如图11所示。

将PID整定参数代入式(29),在Matlab软件中运行,得到液压变桨系统频率特性,如图12所示。

由图12可以看出,快速顺桨时相位裕量为86.7°,增益裕量为8.98 dB,可以判断经过PID整定后系统稳定。

PID整定前,快速顺桨时风力发电机液压变桨系统的阶跃响应时间为4 s。经PID整定后,液压变桨系统的阶跃响应时间为1.8 s。可见,经过PID整定,液压变桨系统可以满足稳定性和响应性能的要求。

图11 液压变桨系统PID控制模型阶跃响应

图12 液压变桨系统PID控制频率特性

7 结束语

基于快速顺桨工况在Matlab/Simulink软件中对风力发电机液压变桨系统进行数学建模,分析液压变桨系统的稳定性和响应性能。通过进行PID控制,提高了液压变桨系统的响应性能。

随着智能技术的发展,智能变桨技术被提出。可以预见,独立变桨、分段变桨、预测变桨、模糊变桨、智能变桨等更加精细和高效的变桨系统将成为未来变桨领域的重点研究方向。

独立变桨可以有效消除风力发电机组的不平衡负载,并且不会影响风力发电机的输出功率[9-10]。但是另一方面,由于风速随机多变,对每个叶片进行独立控制很难实现,因此,独立变桨技术目前仍处于概念阶段。