基于正交法的过盈自锁液压支腿锁紧特性

聂松林,张思淼,张振华,申文强

(1.北京工业大学材料与制造学部,北京 100124；2.北京特种机械研究所,北京 100143)

0 前言

过盈锁紧液压支腿通过缸筒与锁紧套过盈配合实现机械自锁紧，能够可靠锁定在行程内的任意位置，不存在“软腿”现象，在支撑大负载时能够长时间保持良好的锁紧刚度和支撑稳定性，在航空航天、特种工程车辆等领域具有广泛应用前景[1-2]。对于过盈锁紧液压支腿来说，缸筒和螺旋锁紧套间的圆筒过盈连接设计是关系液压支腿能否可靠工作的最关键问题[3]。截至目前，国内外众多学者将理论计算、仿真分析和试验相结合，对圆柱过盈联接结构的弹性变形、弹塑性本构关系等进行了深入研究，并取得了很多有意义的成果。

其中，CROCCOLO等[4-7]建立了多层圆筒过盈配合面接触压力、径向应力、环向应力的数学模型，分析了圆柱面过盈连接接触面的应力特性，并通过有限元进行了验证。LIAO等[8-11]研究了配合公差、轴向载荷量、轴空心度、轴套壁厚等对过盈接触应力的影响，发现摩擦因数对径向接触应力影响不大，接触应力随着轴向载荷量、轴空心度增大而减小，轴套外表面接触应力随轴套壁厚增大而减小，内表面接触应力随轴套壁厚增加而增大。ZHOU等[12-16]将数值分析与试验相结合，研究了粗糙度、接触直径等对轴/轮毂过盈配合应力分布及接触状态的影响，发现表面粗糙度越大，接触应力越大；接触直径越大，接触应力越大。BHARATA等[17]以轴承为研究对象，发现材料对轴承接触应力影响显著，但接触长度对接触应力影响不大。HUANG等[18-19]分析了过盈量、摩擦因数、接触直径、接触长度等过盈配合参数对接触压力、摩擦剪应力、微动疲劳寿命的影响，基于微动损伤参数建立了圆筒过盈微动疲劳的预测模型。LU等[20]采用虚拟正交设计方法，研究了过盈量、摩擦因数对轴毂过盈配合段摩擦功的影响规律，优化得到了过盈配合理想参数。丁问司等[2-3]基于ANSYS对自锁液压支腿进行了静力学分析，得到了液压支腿自锁状态下应力应变分布，研究了环境温度、摩擦因数、接触面积等对锁紧特性的影响。

综上所述，国内外对厚壁圆筒过盈配合的研究重点是分析过盈配合结构参数对圆筒应力变形的影响，主要以轴承、轮毂、行星轮等为研究对象，与过盈锁紧液压支腿的结构及工况差距较大。另外，以上研究大多是遵循单一变量原则，即保持其他因素不变，仅通过改变某一因素来研究其对力学性能的影响，无法明确各因素交互作用的影响，得出的结论往往不够准确。因此，本文作者以某重载自锁液压支腿为研究对象，采用正交法并结合有限元来系统研究环境温度、摩擦因数、锁紧位置及其交互作用对液压支腿锁紧特性的影响，并进行敏感性分析，为自锁液压支腿的设计、研制和工程应用提供理论指导。

1 正交设计

1.1 物理模型

自锁液压支腿主要结构如图1所示，主要由缸筒、活塞杆、活塞等组成，其中活塞又分为上端活塞、锁紧套和下端活塞三部分，通过缸筒与锁紧套之间的过盈联接实现机械锁紧；当向锁紧套螺旋凹槽与缸筒内壁构成的过盈配合腔通入高压油液时，缸筒发生径向弹性变形，使过盈配合变为间隙配合，液压支腿实现解锁。缸筒与锁紧套的过盈配合关系是影响液压支腿锁紧性能的关键，通过建立缸筒与锁紧套过盈配合体的有限元模型，以研究环境温度、摩擦因数、锁紧位置及其交互作用对液压支腿锁紧性能的影响。

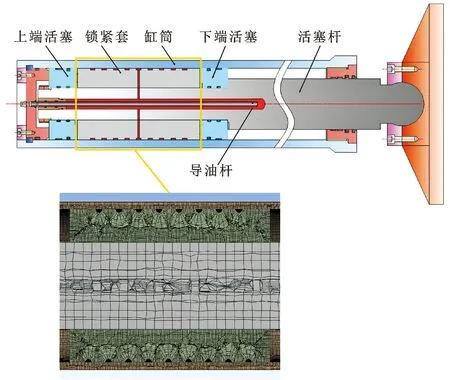
图1 液压支腿结构方案及局部有限元模型

1.2 正交设计

采用正交法进行设计，研究环境温度、摩擦因数和锁紧位置三因素对液压支腿锁紧力的影响，根据实际工况中各因素可能的取值范围，确定的因素水平如表1所示。由此可知，文中正交设计属三因素五水平，故选择正交表L25(56)。将所研究的三因素五水平代入正交表，基于有限元法的正交设计方案及相应的锁紧力结果如表2所示。

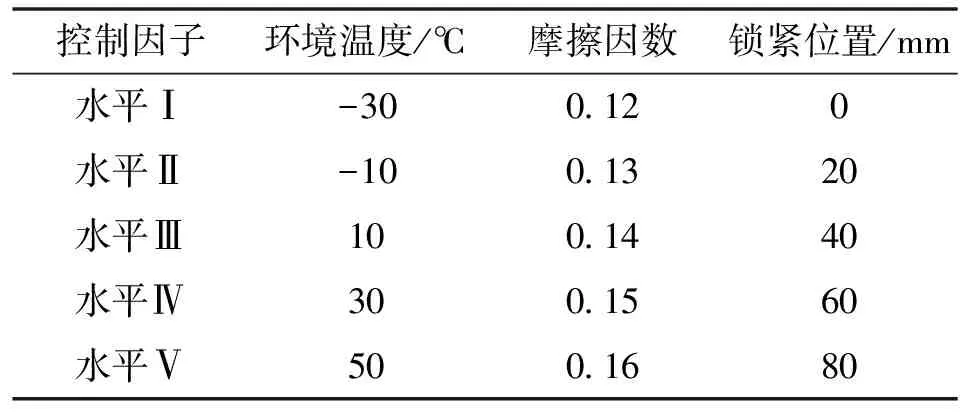
表1 正交设计影响因子及因素水平

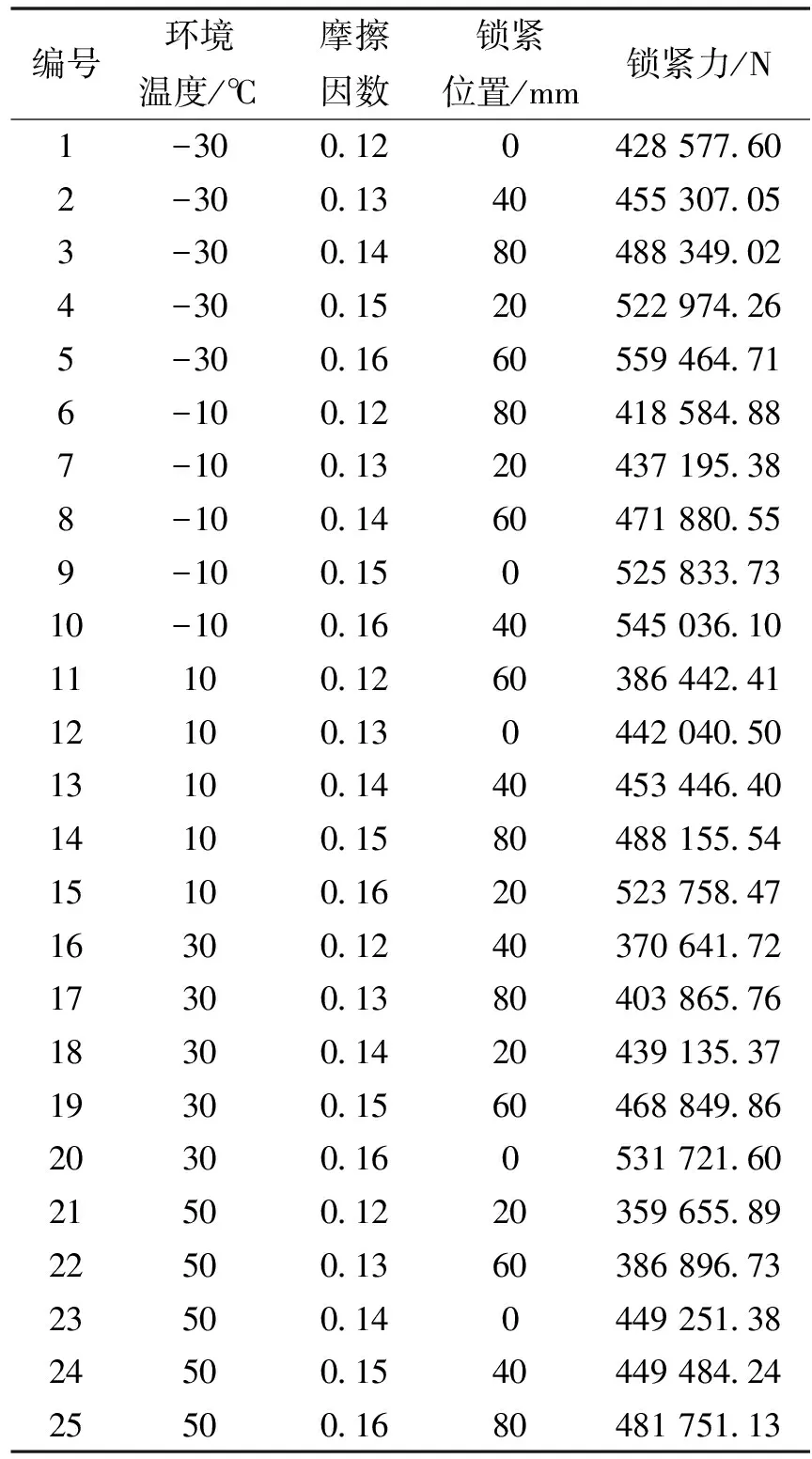
表2 正交设计方案及计算结果

2 结果分析

2.1 锁紧敏感性极差分析

根据计算结果，对锁紧力进行极差分析如表3所示，其中k1～k5分别指各因素在五水平下的锁紧均值，极差R为最大与最小均值差的绝对值。由环境温度、摩擦因数、锁紧位置的R值大小，可以判断出3个因素对锁紧力的影响主次顺序为：摩擦因数>环境温度>锁紧位置。

表3 极差分析结果

为分析各个因素变化对锁紧力的影响，分别以三因素五水平为横坐标，对应锁紧力的均值为纵坐标，绘制的指标-因素关系如图2所示。由此可知：摩擦因数对锁紧力的影响最大，环境温度次之，锁紧位置对锁紧力影响很小。随着摩擦因数的增大，液压支腿锁紧力显著增大；而环境温度对锁紧力有不利影响：随着环境温度增大，锁紧力近似呈线性减小；当锁紧位置超过20 mm时，它对锁紧力基本没有影响。

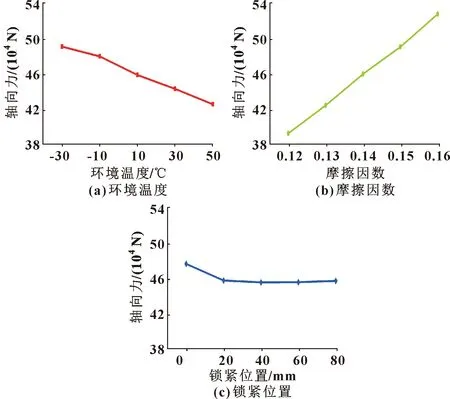
图2 指标-因素关系曲线

然而，由于极差分析存在局限性，不能估计正交计算过程中必然存在的误差大小，即不能区分某个因素各个水平所对应的计算结果差异，究竟是由于因素水平不同引起的，还是由计算误差所引起的，因此无法保证分析精度。为了弥补极差法的这一缺点，还进行了方差分析。

2.2 锁紧敏感性方差分析

在方差分析中，显著水平α=0.01下无显著结果时，将接受原假设，即认为该因素对指标影响不显著。方差分析结果如表4所示，其中计算误差所产生的影响由误差项e表征。查F分布表可知，F0.01(4,12)=5.41。比较F值和F0.01大小可知，有99%的把握认为3种因素对锁紧力的影响显著。通过比较3种因素均方大小，可知3种因素对锁紧力的影响顺序为：摩擦因数>环境温度>锁紧位置，即摩擦因数对锁紧力的影响最大，环境温度次之，锁紧位置对锁紧力影响最小，这与极差分析结果一致。

表4 方差分析结果

2.3 锁紧敏感性回归分析

基于以上极差、方差分析结果，对锁紧力进行回归分析，得到锁紧力Y与环境温度t、摩擦因数f和锁紧位置l之间的经验公式为

lnY=-0.026 484 2t+7.322 049f-0.000 032 8l2+0.346 667 7tf+3.79×10-7l3-1.195 226tf2-1.01×10-7tl2+12.042 44

即：

Y=eX

其中：

X=-0.026 484 2t+7.322 049f-0.000 032 8l2+0.346 667 7tf+3.79×10-7l3-1.195 226tf2-1.01×10-7tl2+12.042 44

根据上述经验公式，可得到不同工况下环境温度、摩擦因数和锁紧位置与液压支腿锁紧力的函数关系。为判定回归模型拟合精确度，对回归模型和回归系数进行显著性检验(结果如表5、表6所示)。由表5可知，P=0.000 0(P<0.000 1)，锁紧力的回归方程高度显著。由表6可知，各回归系数P值均小于0.1，表明表中各项系数均显著。

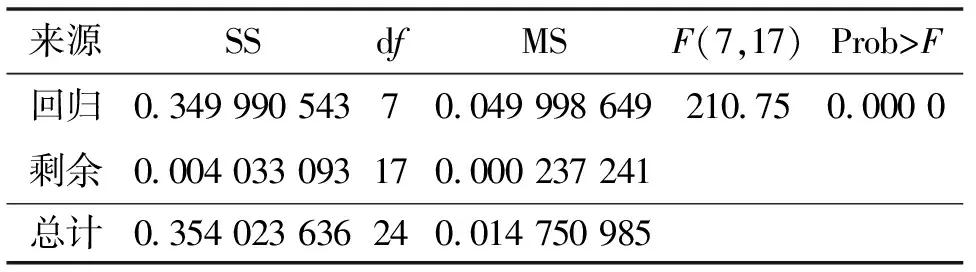
表5 回归模型显著性检验结果

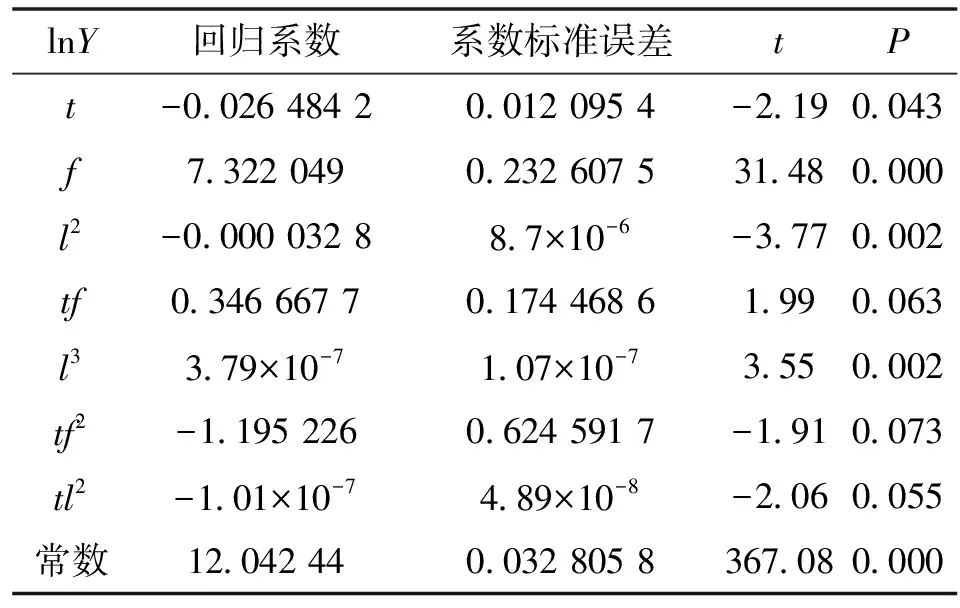
表6 回归系数t检验结果

为更加直观地验证回归方程的可信性，重新对环境温度、摩擦因数和锁紧位置的不同水平值进行组合计算，并将各因素的取值代入回归方程，获得解析结果，与数值计算结果进行对比，获得相对误差。回归方程的解析与仿真结果比较如图3所示。由此看出：两结果相对误差很小，解析结果与数值仿真结果接近程度很高，说明回归方程可信。

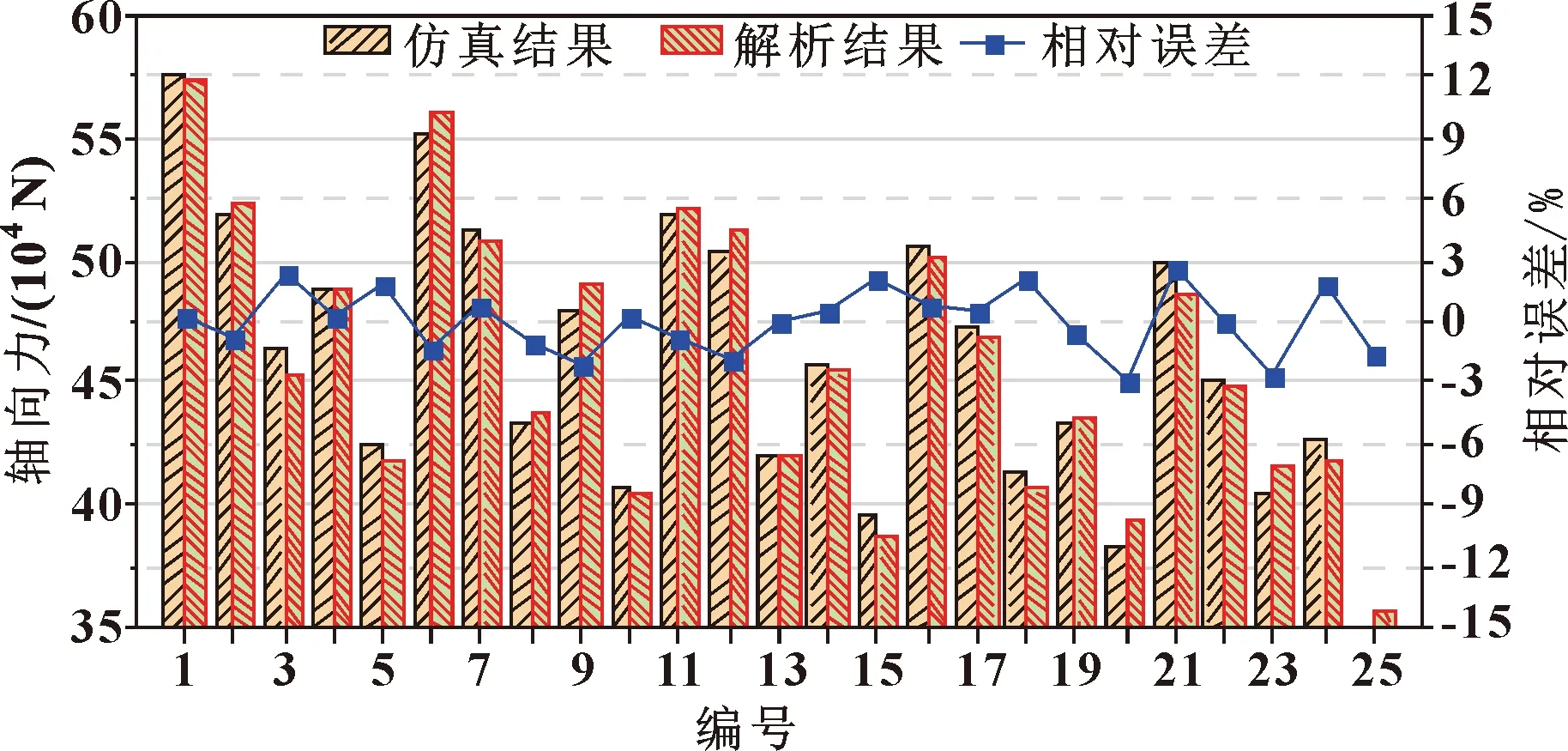
图3 回归方程理论与仿真结果

3 结论

以重载自锁紧液压支腿为研究对象，将有限元法、正交法相结合，系统研究了环境温度、摩擦因数、锁紧位置对液压支腿锁紧性能的影响，并进行了敏感性分析，获得以下结论：

(1)通过极差分析和方差分析可知，环境温度、摩擦因数、锁紧位置对液压支腿锁紧力的影响顺序为：摩擦因数>环境温度>锁紧位置；

(2)通过极差分析可知，液压支腿锁紧力随摩擦因数的增加显著增大；随环境温度的增高近似线性减小；随着锁紧距离的增加逐渐减小，且减小趋势趋于平缓。

(3)通过回归分析获得了锁紧力与环境温度、摩擦因数和锁紧位置之间的经验公式，并通过数值方法检验了经验公式的拟合效果，表明该经验公式能够较为准确地反映不同工况下液压支腿的锁紧性能，为不同工况下自锁液压支腿的应用提供参考。