基于Hermite方法的机器人任务空间二阶平滑位姿路径构造

梁艳阳，王利，姚超智，王琼瑶

(五邑大学智能制造学部, 广东江门 529000)

0 前言

随着科技的进步，工业机器人被应用于生活的各个领域中[1]，人们对工业机器人的需求越来越广泛，对其精准度、灵活性等性能的需求也日益增加[2]。在工业应用中，对工业机器人进行轨迹规划是机器人运动控制的基础，而构造平滑且连续的位姿是保证工业机器人能够实现平稳运动的核心技术[3-4]，是轨迹规划中需要重点研究的领域[5-6]。

路径构造和优化问题备受研究者们关注。文献[7]在空地异构机器人系统中为使空中无人机和地面无人车的路径高度耦合，采用遗传算法与蚁群算法相融合的方法对两者的路径进行优化求解，但该方法仅限于对均匀离散点的路径规划，没办法适用于各类复杂的工作环境；文献[8]利用贝塞尔曲线对机器人路径进行优化，此方法虽缩短了运动路径，但无法满足机器人在某些特定点的运动；文献[9]通过引入基于三角不等式的剪枝策略对路径拐点进行平滑处理，从而优化局部路径段再达到优化全局路径段的目的，此方法虽然对路径优化做了一定的改进，但改进效果还有些不足。针对以上存在的问题，本文作者将机器人在运动过程中会遇到的所有复杂路径进行统一规划，将机器人运动路径分为基本路径和过渡路径，对两种情况分别予以讨论。

工业机器人的连续位姿路径包括位置路径和姿态路径，位置路径一般包括直线、圆弧等基本路径。位姿路径表达方式有旋转矩阵、欧拉角、四元数、轴-角等方式，旋转矩阵、欧拉角、轴-角在路径插补或轨迹过渡时存在缺陷或者效率问题，因此用四元数[10-11]来统一描述姿态问题。而关于路径过渡，过渡路径包括位置过渡路径和姿态过渡路径[12]。Hermite曲线作为空间曲线，完全可以应用于位置过渡和空间过渡的求解中。面对当下工业机器人复杂的运动环境和各类不同的运动轨迹，也需要设计一种适用于各类不同路径的过渡方法。本文作者应用Hermite方法[13]在过渡区构造曲线，使得机器人运动在遇到各类复杂的路径情况时都可平稳运行。

1 基本位姿路径构造

1.1 基本位置路径构造

路径包括直线、圆弧、关节、姿态及其组合等多种情况。自动程序运行，原则上主要有直线段、圆弧和关节这3种基本路径，但是在实际情况中，可能存在纯姿态路径，位置(直线、圆弧)和姿态路径同时存在，过渡路径(多段组合)。在这里作者主要讨论直线段、圆弧这两种基本的位置路径构造。

1.1.1 直线路径构造

P=v·x

(1)

式中：v表示运动方向，即v=(pe-ps)/L。

1.1.2 圆弧路径构造

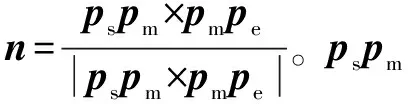
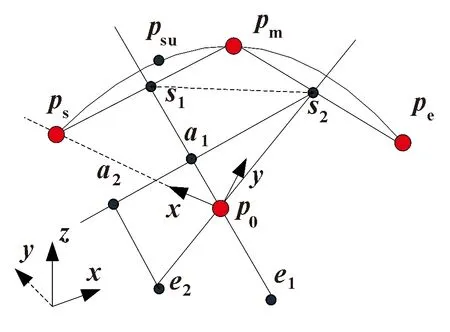
图1 构造圆弧

定义

(2)

中垂线s1e1的单位方向向量ns1e1=n1，中垂线s2e2的单位方向向量ns2e2=n2，从而求得圆心位置

(3)

其中：|s2a1|为投影点a1到s2长度;|s2a2|是s2e2在s2a1上的投影长度。

p0ps的单位向量np0ps，p0pe的单位向量np0pe，圆弧角α=arccos(np0ps·np0pe)，圆弧上确定一个支持点psu，圆弧相对于参考坐标系姿态为

R=[noa]

(4)

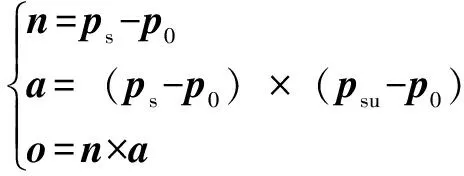
1.2 姿态路径构造

机器人姿态一般可通过旋转矩阵、欧拉角、四元数、轴-角等方法表示。旋转矩阵、欧拉角和轴-角在路径插补或轨迹过渡时存在缺陷或者效率问题，因此本文作者以四元数统一处理姿态路径构造。

1.2.1 四元数表达式

四元数一般表达式为

q=w+xi+yj+zk

(5)

其中:w,x,y,z是实数;i,j,k是虚部，且满足下式。

(6)

四元数还能表示为：[w,v]或者[w,(x,y,z)]，式中w是标量，v=(x,y,z)是矢量。如果|q|=1，则q为单位四元数。

1.2.2 四元数的指数和对数

q=[cosθ,sinθ·v]为单位四元数，则对数为

log(q)=[0,θ·v]

(7)

q=[0,θ·v]，则其指数为

exp(q)=[cosθ,sinθ·v]

(8)

1.2.3 四元数的共轭和逆

令q=[cosθ,sinθ·v]，则其共轭为

q*=[cosθ,-sinθ·v]

(9)

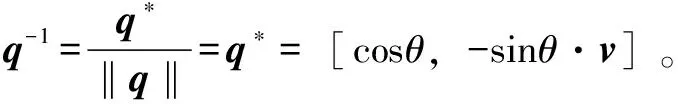
1.2.4 四元数乘法

q1=[s1,v1]，q2=[s2,v2]，则有：

q1q2=[s1s2-v1·v2,v1×v2+s1v2+s2v1]

(10)

1.2.5 球面线性插值

给定两个单位四元数p和q，其球面线性插补计算公式为

Slerp(p,q,h)=p(p*q)h=(pq*)1-hq=

(qp*)hp=q(q*p)1-h=Slerp(q,p,1-h)

(11)

一阶导数为

(12)

其弧长积分为

(13)

其中，可以计算确定|β|为两个单位四元数向量之间的夹角大小，因此四元数球面线性插补的总弧长可以通过计算两向量的夹角这种方式得到。

2 基于Hermite方法的二阶平滑位姿路径构造

在连续轨迹运动时，相邻路径之间需要进行平滑过渡[14]，因此，需要构造两段相邻路径之间的过渡路径。过渡路径的构造涉及的问题较多，如：前后路径参考坐标系不同，任务空间前后路径不在同一平面上，前后路径分属任务空间或关节空间，前后路径分别有或无姿态，前后路径分别有或无位置变化等。这些问题都可以通过适当的处理，最后核心问题就是位置过渡路径和姿态过渡路径的平滑构造。

2.1 位置过渡路径构造

位置过渡路径一般分为3种情况：(1)直线与直线之间的过渡：(2)直线与圆弧之间的过渡;(3)圆弧与圆弧之间的过渡。3种情况下的过渡路径原理相同，处理步骤为：(1)根据过渡半径或过渡区大小确定过渡点以及支持点；(2)构造Hermite路径曲线；(3)数值积分方法计算曲线的弧长。

以圆弧与圆弧之间的过渡曲线为例，如图2所示，给定任务空间位置过渡区大小(zone)，首先计算得到前后两条路径的过渡点为qa和qb，然后根据前后路径曲线方程计算qa和qb处的两条切线，在两切线的延长线上选择距离为d=min(Lpapb/4,Dmax)得到辅助点qc和qd，其中Lpapb为过渡点qa和qb的距离，Dmax为给定的最大距离参数。

图2 任务空间位置过渡曲线

根据qa、qc、qd和qb，可以构造3次Hermite曲线方程：

P(u)=(1-u)3P1+3(1-u)2uP2+3(1-u)·

u2P3+u3P4

(14)

上述曲线方程的一阶导数为

(15)

其中：P1=qa,P2=qc,P3=qd,P4=qd。

2.2 姿态路径的过渡路径构造

如图3所示，根据给定的过渡区大小(zone)，计算确定过渡点qa和qb。姿态路径采用球面四元数曲线，所以可以根据式(12)球面线性插值方程的一阶导数计算角速度ωa和ωb，最终得到Hermite四元数插值曲线方程为

(16)

其中：

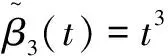
q0=qa

q1=qaexp(ωa/3)

q2=qb(exp(ωb/3))-1

q3=qb

该Hermite四元数插值曲线方程的一阶导数为

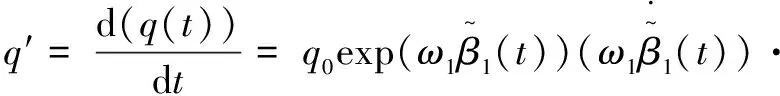
(17)

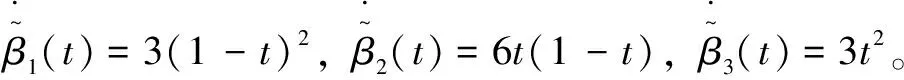
3 位姿路径长度计算及插值

3.1 基于数值积分方法计算路径长度

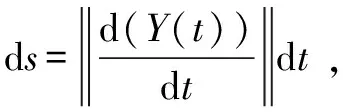
(18)

上式一般需要通过数值方法进行求解，只需要满足工程上足够的精度即可。数值积分的方法较多，这里采用4阶Newton-Cotes积分方法进行计算。其计算公式为

12f(x2)+32f(x3)+7f(x4)]

其中:xi=a+ih(h=(b-a)/4,i=0,1,2,3,4)。

设计如图4所示的迭代算法[15]完成给定精度的位姿路径长度计算:

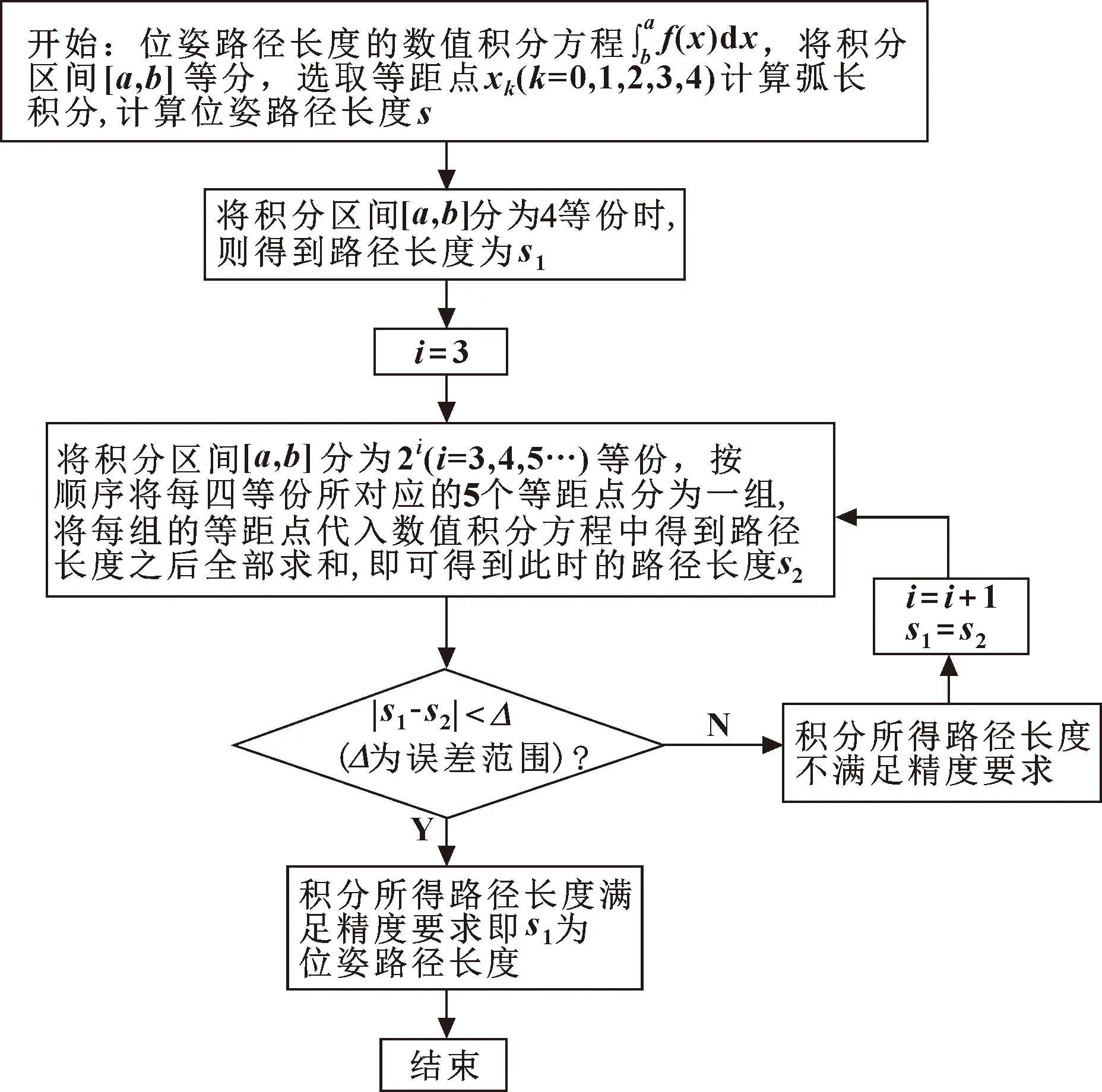
图4 计算位姿路径长度的算法流程

3.2 基于数值积分及二分查找实现插值

在速度规划中，一般给定路径长度要求得到对应的路径点。直线、圆弧所描述的位置路径以及一般的四元数表示的姿态路径都可以直接得到解析解，而文中所构造的过渡位姿路径，只能通过数值算法计算得到给定精度的数值解。

令曲线参数方程为Y(t)，弧长方程为s(t)，给定弧长为s，用数值方法求取s对应的曲线参数t。将所得t值代入到曲线参数方程Y(t)，即可得到给定弧长对应的点坐标。结合弧长的数值积分和二分查找算法，设计如图5所示的算法实现给定路径长度所对应插值点的计算。

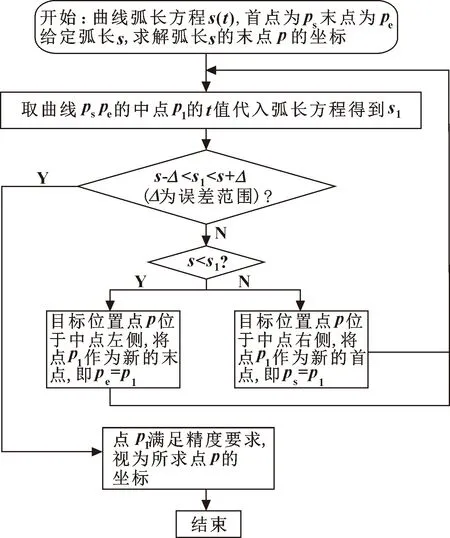
图5 给定路径长度查找插值算法

4 数值仿真及分析

为验证文中方法的正确性和准确性，将算法转化为MATLAB代码，进行仿真实验，验证基于Hermite方法的机器人任务空间二阶平滑连续位姿路径构造的可行性。

4.1 位置过渡曲线仿真

随机选取一组数据，确定直线与圆弧之间的过渡曲线。如表1所示，随机选取空间中三点(起点ps，中点pm，终点pe)确定一条空间圆弧，再在空间中选取两点(起点ps，终点pe)确定一条直线，且直线和圆弧有交点，根据实际应用情况确定过渡区及过渡点qa、qb，应用Hermite方法构造位置过渡曲线。仿真结果如图6所示。

表1 随机确定的圆弧和直线及过渡点

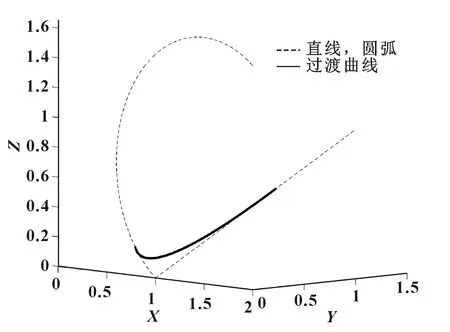
图6 直线和圆弧过渡仿真结果

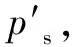
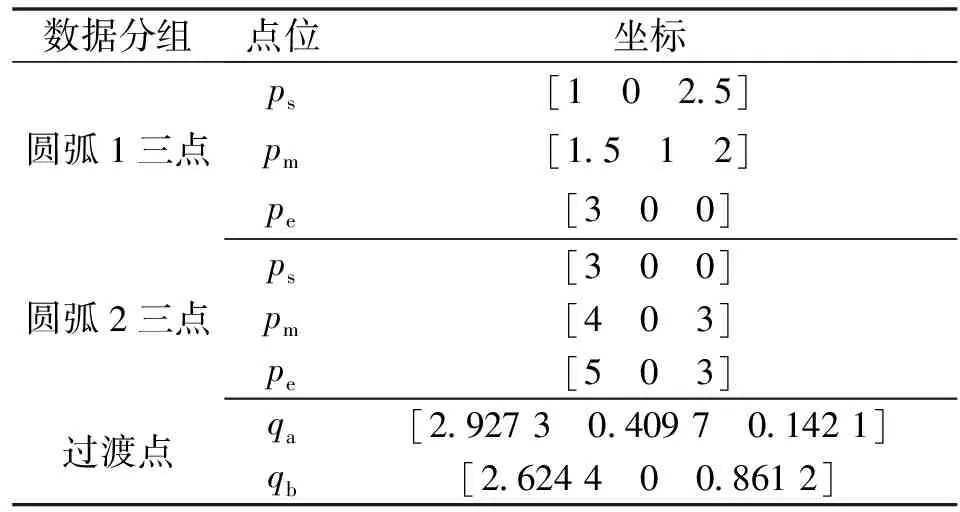
表2 随机确定的两圆弧及过渡点

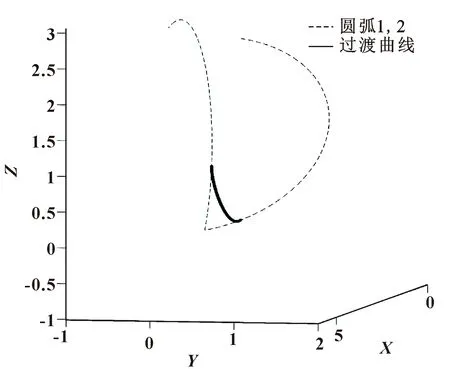
图7 圆弧与圆弧过渡仿真结果

根据以上两种情况的位置过渡曲线以及仿真结果可以确定在已知过渡区或过渡点的情况下，根据Hermite方法构造的过渡曲线可以达到平滑的位置过渡路径的要求。

4.2 位姿过渡曲线仿真

如表3所示，随机确定3组数据，每组数据为随机选取的3个四元数作为示教点，通过3个示教点中的起点、中点和末点确定两段直线或圆弧，根据实际应用情况确定好过渡点或过渡区，从而根据Hermite方法构造过渡曲线。

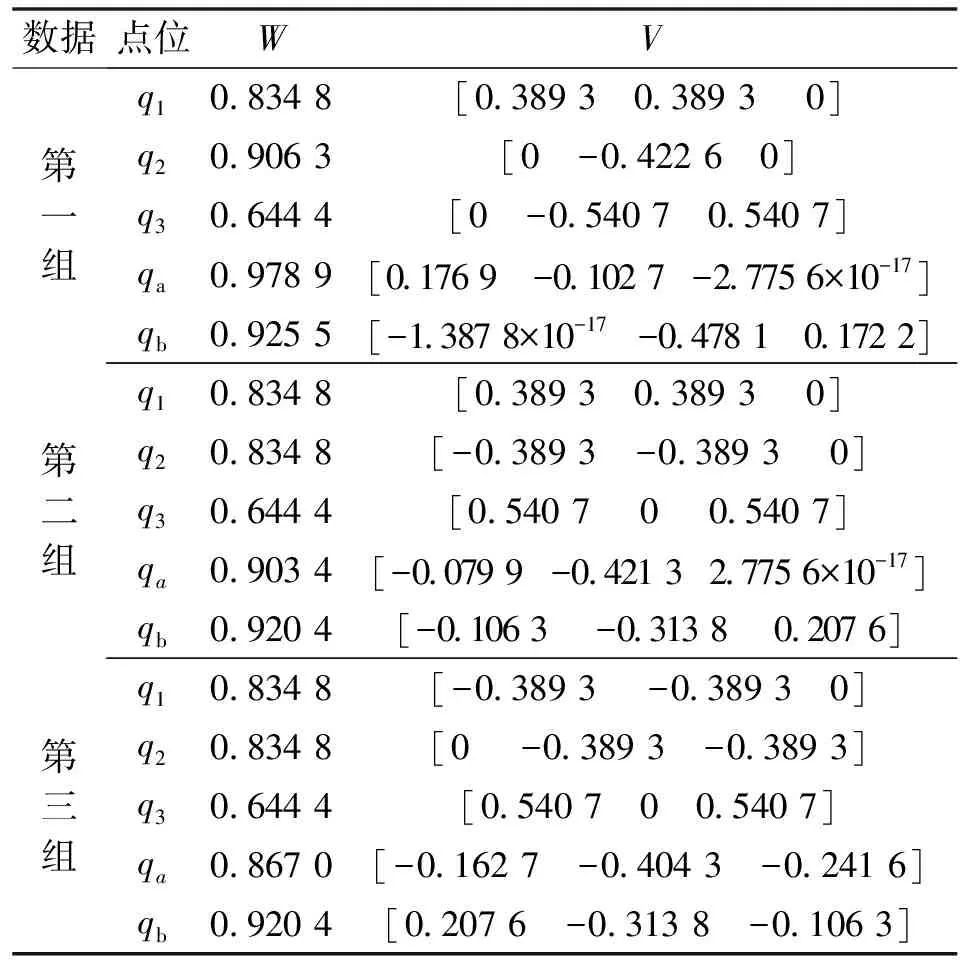
表3 随机确定四元数曲线及过渡点

仿真结果如图8—图10所示。

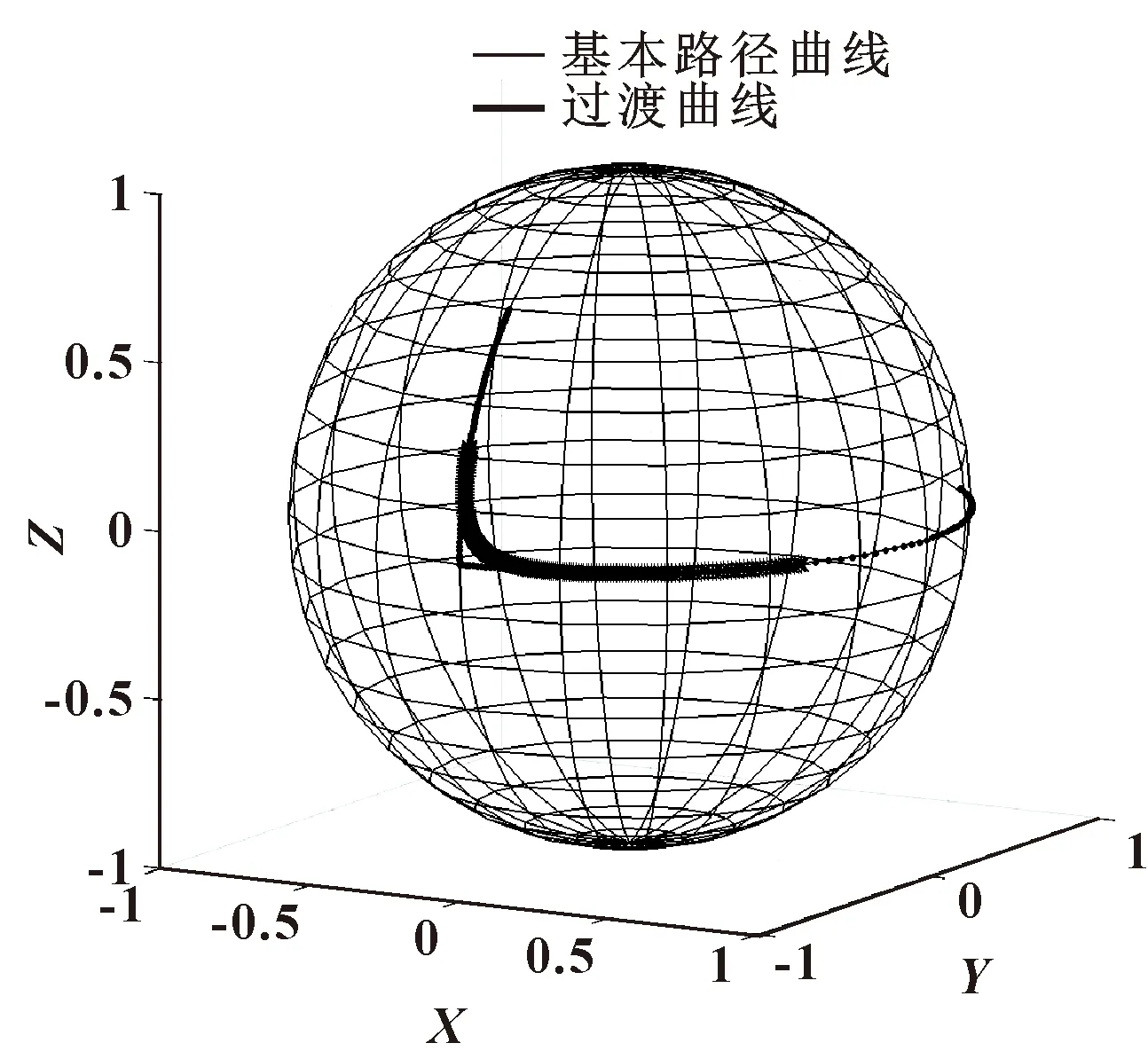
图8 第一组数据仿真结果

第一组3个四元数所构成的两段圆弧成90°角，在确定过渡点的情况下应用Hermite方法构造过渡曲线，且构造的过渡路径足够平滑,如图8所示。同理第二组3个四元数所构成的两段圆弧成小于90°角，如图9所示；第三组3个四元数所构成两段圆弧成大于90°角，如图10所示。因此可以得出结论:不论两段圆弧所构成角度是大于90°或小于90°，都可以在确定过渡点的情况下应用Hermite方法构造的过渡曲线，且构造的过渡路径足够平滑。因此任意3个点都可通过该算法构造出可供工业机器人平稳运动的路径。经过仿真，验证了该算法的通用性和有效性。

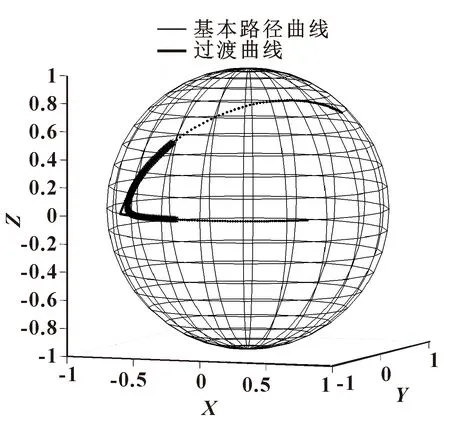
图9 第二组数据仿真结果

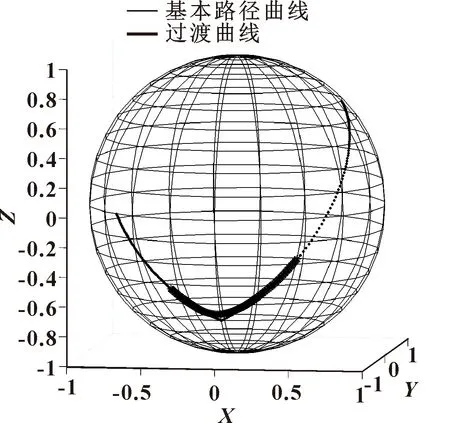
图10 第三组数据仿真结果

5 结论

为使机器人在复杂的工作环境中都可以平稳运行，将Hermite方法应用于机器人位置过渡路径和姿态过渡路径，并在MATLAB中进行仿真实验。实验结果表明:Hermite方法可以满足机器人在任意的运动环境或情况下的运动路径平滑过渡的需求。此研究在前人研究的基础上更加优化了机器人路径构造算法，促进了工业机器人运动轨迹方面研究的发展。此研究的遗留问题是工业机器人的轨迹规划问题，在此研究的基础上再进一步进行机器人轨迹规划是接下来需要去研究的课题。