加强课堂训练 提升思考能力

江苏省木渎高级中学 朱雪民

波利亚认为：“教会学生有目的的思考，是数学教学的基本目标之一.”[1]思考是思维的一种探究活动，是人类对意向信息进行加工的过程，所有思考的进行都存在联想的参与.数学思考是指从数学的角度，用数学的思维对数学对象进行思考的过程，这种思维方式是形成创新能力的核心.数学抽象、推理与思维是数学思考的灵魂，也是形成数学思想的基础.高中数学相对抽象，如何立足于当堂训练，提升学生的思考能力是笔者近些年一直在研究的问题.本文从以下三点展开阐述.

1 加强复述训练，启发思考

教学中，不少学生对一些数学知识处于“能意会，却无法言传”的状态，这种情况常导致学生在解题时出现思维模糊、想着想着就跑偏了的现象.而复述是训练学生思考能力的基本手段之一，它能让学生清晰思维、明晰解题思路.

所谓的复述是指将所学内容，用自己的语言进行流畅地表达.这种方式能将学生思维的“图式”呈现出来，让学生在多次重复的复述训练中不断完善并丰富自己的思维结构.相对而言，高中数学有些语言比较拗口、抽象，要让学生完整地通过自己的语言准确表达出来，实非易事.但为了启发学生对所学内容的思考，以训练学生的思维能力，还需要鼓励学生勤加训练,长期坚持才能真正达到启发思维的效果.

例1“曲线的方程”与“方程的曲线”的概念复述.

从字面上来看，这两个概念异常相近.它们之间到底存在怎样的区别与联系？这是本节课教学的重点与难点.为了让学生彻底弄清这两个概念，笔者在教学时先与学生共同探讨这两个概念：

在直角坐标系中，若曲线C上的点和某个二元方程f(x,y)=0的实数解建立以下两点联系：①曲线上点的坐标全都是该方程的解；②以此方程的解为坐标的点，这些点均为曲线上的点.那么，此方程为曲线的方程，此曲线为该二元方程的曲线.

学生在课堂上虽对此概念有了一定的了解，但若不加以复述或巩固，不少学生过两天就开始混淆，理不清楚其中的关系.为此，笔者在当堂课即带领学生进行复述训练，以深化学生对这两个概念的理解.而复述的过程则体现了思维活跃的过程，此过程能有效地启发学生的思考.

复述：

(1)从定义中的两个条件来复述

这两个条件反映了曲线上的点和以方程的解为坐标的点，二者是不多不少，恰合适的关系.从第一个条件来看，曲线上的点不多于方程的解为坐标的点，也就是曲线上的点全都符合条件，没有一点是例外的；从第二个条件来看，曲线上的点不少于方程的解为坐标的点，也就是说所有符合条件的点均于这条曲线上，没有遗漏.

(2)从集合的角度复述

将曲线理解为点的集合，记作C；将方程的实数解理解为点的坐标，点集记作F.

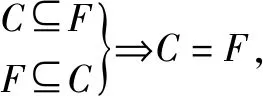
也就是C={(x,y)|f(x,y)=0}.

从这两个角度进行复述的情况来看，复述训练能有效地启发学生的思考，让学生从自身独有的思维角度去分析与理解知识的内涵.此过程是内化新知、建构认知体系的重要过程，亦是赋予所学知识价值的过程.

2 强化变式训练，深化思考

众所周知，变式训练是相对于某种范式的变化形式，是深化学生思考，提升解题能力的重要途径之一[2].变式一般是将简单的概念、公式、性质等演变成复杂问题的过程，一旦掌握了变式的基本思想，就能掌握解决问题的基本策略与方法.这种训练方式，对提高学生的辩证思维能力以及思维的自觉领悟能力具有重要影响.

教学中，我们常涉及到的变式有语言、图形、概念、定理、公式或题目等，不论是哪种变式的应用，均以知识和文化两大导向为基础，以实现教学的三维目标为宗旨.我们接触最多的是试题的变式，即以一道试题为母胎，为了深化其知识的内涵，通过问题条件或结论的变化，呈现出一组新题.通过这组问题的解决，在完善原有认知结构的基础上深化思考，形成良好的数学综合素养.

例2已知在数列{an}中，a1=1,an+1=an+1(n∈N*)，求该数列的通项公式.

变式1已知在数列{an}中，a1=1,an+1=an+n(n∈N*)，求该数列的通项公式.

变式2已知在数列{an}中，a1=2n-1,an+1=an+2n-1(n∈N*)，求该数列的通项公式.

解析：形如an+1=an+f(n)的递推关系式，可采用叠加的数学思想，将问题化归成等比或等差数列求和.

变式3将原式中an前面的系数变为2，也就是an+1=2an+1，求此时数列的通项公式.

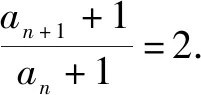
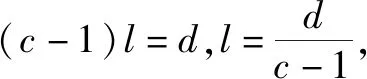
变式4将变式3中的常数改成幂的形式，如an+1=2an-3n，求此时数列的通项公式.

解析1:与变式3类似，把递推公式变形成an+1+3n+1=2(an+3n)，从而凑配为等比数列{an+3n}，计算可得an=2n+1-3n.

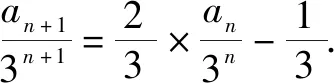
综上，想要深化学生对知识纵深的理解，变式训练是最好的方法之一.通过以上变式的应用，学生不仅对此类问题有了更为深刻的认识，在脑海中建构了一系列求解的通项公式，当再次遇到类似问题时，则能举一反三，顺利解题.在此变式训练的过程中，学生在获得知识的同时，还形成了良好的思考能力，为各项数学能力的提升奠定了基础[3].

3 运用感悟训练，提升思维

曾子有云：“吾日三省吾身.”反思是促进思维成长的利器，是提高人类各项能力的保障.“悟”即深层次的思考与反思，它是学习者思维能力的体现.那么，在数学课上，学生应该从哪些角度去进行感悟呢？笔者认为有以下几点：

(1)基础知识的感悟

教学遵循一个循序渐进的过程.课堂教学一般从基础的概念、定理或公式出发，这些基础性的知识虽然简单，但若扣不住它的核心点，不弄清它的发展主线，则无法深刻认识其内涵与外延.而课堂时间又是有限的，有些问题教师并不能讲得非常全面、透彻，尤其是在“以学生为主体”的背景下，更多的是教师的点拨与学生的自我领悟.因此，这就要求学生要拥有“悟”的意识，从不同视角去审视与感悟基础知识，达到知其然且知其所以然的境界.

(2)解题方法的感悟

数学能力的高低可在解题中见分晓，良好的解题方法，为思维指明决策程序，为后期学习中的类比提供保障.对解题方法的感悟，最重要的是要注重思考解题方法的主要特征、基本步骤、技巧等，并将这些内容内化到自己原有的认知结构中，将良好的解题技巧与方法转化为自己的技能.

(3)数学思想的感悟

解题方法与技巧属于实施层面的内容，而其背后一般都蕴藏着一定的数学思想，这些数学思想则属于数学的灵魂.数学思想决定了数学学习的整体策略与方法，是学生真正实现触类旁通的关键因素.因此，教学中应注重加强学生对数学思想方法的感悟.学生一旦领悟了相应的数学思想方法，则能从真正意义上实现以一通百的能力.

总之，提升学习效率是教学的首要任务，训练学生的思考能力具有重要的战略意义.作为教师，应结合学情与教学内容，在授学环节，选择合适的方式进行思考能力的训练，让学生在复述、变式与感悟中不断地提高自身的学习能力与数学核心素养.