在数学思想方法的指导下构建高效复习课堂
甘肃民勤县教师进修学校 运其书
近几年来,高考已将数学思想方法的考查作为一项重点内容,为此,在高三复习阶段应重视学生数学思想方法的渗透,化思想为动力,化方法为能力,构建高效数学课堂.笔者在高三复习阶段做了一些尝试,取得了一些效果,以期抛砖引玉,共同成长.
1 复习基础,优化认知结构
基础知识的复习和巩固是高三数学复习的一项基本任务,是学生成绩提升的前提保障.在复习基础知识时,应注意揭示和总结重要的数学思想方法,进而使基础知识更加丰富、生动,从而激发学生的复习热情,促进复习效率提升[1].
例如,在复习指数函数y=ax和对数函数y=logax时,应渗透分类讨论思想,引导学生关注底数a分为a>1和0 很多数学知识间存在着一定的关联性,为了知识间可以更好地沟通和联系,在梳理知识时就要渗透数学思想方法,发挥其纽带的作用,帮助学生科学地建构知识体系,进而优化学生认知结构,提升学生综合素质. 函数思想作为重要的数学思想,不仅在解决函数问题时有着重要的应用,而且也有效地沟通了方程和不等式,为此,将三者合理地联系与转化,极大地丰富了原有认知,有利于知识的迁移和转化.另外,运用数形结合思想将函数图象与方程、不等式的解紧密相连,有利于实现数学知识的优化和整合,有利于解题效率的提升. 因此,在高三阶段,要重视数学思想方法的渗透和提炼,进而将不同模块的知识通过联想和转化进行有效的重组,逐渐建立系统的、全面的认知体系,进而提高学生的综合应用能力. 解题教学是高三复习阶段的重点课型,通过解题反馈的信息及时查缺补漏,可有效提升学生解题能力.解题过程实质就是通过合理的联想和转化将题设信息与结论建立联系,运用分类讨论、数形结合等数学思想进行加工和分析,进而逐渐缩小题设信息和结论的差异,找到合适的切入点,高效求解问题[2].在解题过程中合理运用数学思想方法是解题的关键,有利于解题策略的优化,有利于解题效率的提升. 分析:本题若从代数的角度求解,不仅计算比较复杂,而且容易出现思维障碍,仔细观察式子特征不难发现其与两点间的距离公式息息相关,为此通过挖掘题设的几何意义,运用数形结合思想将代数问题几何化,从而为顺利求解带来了便利. 通过解题过程容易发现,灵活应用数形结合思想使代数问题几何化,进而应用平面几何的相关知识顺利地求解了问题,培养了学生数形建模能力. 很多数学问题都存在一定的规律,若不关注规律,很容易将思维引入死胡同,不仅难以求解,而且容易挫伤学生的学习信心.例2的求解过程是先从特殊出发,发现了隐藏于结论中的一般规律,通过充分联想推理出了f(x)+f(1-x)=1.通过特殊到一般的转化,学生的思维豁然开朗,解题思路也应运而生. 例3若不等式(lgx)2-(2+m)lgx+m-1>0对|m|≤1恒成立,求x的取值范围. 分析:观察题设信息,学生易于将不等式看成关于lgx的二次不等式,但求解时不仅需要分类讨论,而且运算复杂,即使能够求解也需要较长时间,显然这种方法是不可取的,为此需要另辟蹊径.既然将lgx看成未知难以求解,是否可以将其视为已知呢?将常量和变量进行转化,将不等式转化为关于m的一元一次不等式,于是构造函数f(m)=(1-lgx)m+[(lgx)2-2lgx-1],这样将主参换位有效地规避了繁琐的讨论,使其转化为常规问题,此时求解x就变得简单方便了. 可见,在面对复杂的数学问题时,合理转化可以实现化繁为简.在高中数学教学中渗透数学思想,可以有效地避免思维定式给解题带来的局限性.有时候通性和通法不适宜问题求解时,要学会变通,及时转换思路,这样往往可以收获意外的惊喜. 数学问题是千变万化的,在解题过程中靠死记硬背不仅学得累,而且很难提升解题效率.若想既快又准地解决问题,就要重视培养思维的变通性,即当固定方案行不通时,需要重新观察和挖掘题设信息,通过联想和分析知识点间的相关性,寻找最优解决方案[3].要完成这一过程需要注意训练以下几种能力. (1)观察 解题首先要通过观察提取有价值的信息,进而通过对信息的整合找到解题的合理切入点.数学条件和数学关系或显性或隐性地蕴含于题目中,要想解决问题就要依据题目的结构特征,通过深度观察和剖析,找到问题的本质特征,进而确立解题思路.在解题时切勿急于求成,要善于从整体去观察和解读.如果看到题目就解,解不下去再更换思路,这样将严重影响解题效率.为此,解题时要进行细致、透彻地观察,厘清问题的来龙去脉后再求解,这样可使解题更高效. (2)联想 联想是通往成功的必经之路.众所周知,高中数学题目是复杂的,在解决一个问题时往往会涉及到很多内容,而这些内容的联系往往并不明显,通过观察找到题设的特征后,应用联想将这些相似、相关的内容串联起来,形成一个较为完善的思维脉络,灵活应用所学知识进行迁移和转化,巧妙解决问题. (3)转化 转化是解决数学问题的法宝.大多数学问题都是在转化中完成的,例如,当遇到比较复杂的问题时常将其进行拆分,将其转化为较为熟悉的、简单的问题,进而化繁为简;当遇到比较抽象的内容时,常与生活实践相联系,从而在具体的情境中进行联想和转化,使问题化抽象为具体.当然还有化未知为已知,化新知为旧知,等等.总之,在解题时要通过合理联想寻求转化关系,才能高效解决问题. 数学思想方法蕴含于不同的基础知识之中,应用于不同的数学问题之中.若想让学生明晰和领悟数学思想方法的价值,在教学中就应对数学思想方法进行及时的总结和归纳,进而通过提炼和概括强化学生对数学思想方法的认识. 例如,以数列为例,在推导等比数列求和公式时,分类讨论q的值,体现了分类讨论思想;在解决数列递推问题时,常常需要应用等价转化思想;等等.同时,在解题时还需要应用换元法、配方法等重要的数学方法.通过有效的提取,让学生抓中解题的重点和核心,进而为合理转化提供必要的前提. 当然,在复习阶段还可以设置专项训练,以数学思想方法为主线将相关知识进行串联,进而在深刻领悟数学思想方法重要价值的同时,促进思维能力的不断提升. 总之,在教学中要引导学生关注数学思想方法,使之成为优化学生认知结构,发展学生思维能力,提升学生分析问题和解决问题能力的法宝.2 巩固练习,提升解题能力
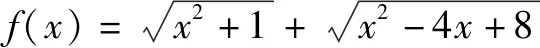



3 归纳总结,深化思想

