一种基于积分滑模观测器的永磁同步电机磁链重构方法
刘晓燕,杨 瑶,龚事引,李佳俊
(1.湖南铁路科技职业技术学院 铁道工程与信息学院,湖南 株洲 412006;2.湖南中医药高等专科学校 护理学院,湖南 株洲 412012;3.湖南工业大学 轨道交通学院,湖南 株洲 412007)
1 研究背景
永磁同步电机(permanent magnet synchronous motor,PMSM)具有高功率因数、高效率、体积小和质量轻等优势,与异步电机相比,具有更大的发展潜力[1-2]。此外,PMSM 具有过载能力强、启动转矩大、可靠性高、转速平稳、噪声低且能在全速范围内提供恒转矩等优点[3-4]。因此,PMSM 逐步成为轨道交通领域最有发展潜质的电机之一,成为下一代列车牵引电机的发展方向[5]。相对于固定场所的永磁电机,应用于轨道车辆的PMSM 运行环境显得更加恶劣,在运行中易受到强电磁干扰、大振动冲击、大温差与大湿度变化等众多不确定因素的影响,造成转子永磁体极易出现失磁故障[6]。一旦出现失磁故障,采用标准数学模型设计的PMSM 驱动器便与电机实际运行情况不吻合,而参数失配不可避免会导致PMSM 驱动器的性能降低,严重时会导致电机报废。为能够及时降低发生失磁故障的风险,确保PMSM 的安全运行,对其失磁故障的在线检测与重构显得尤为必要。
目前,针对失磁故障的检测问题,以观测器对磁链信息进行检测重构来实现对失磁故障的诊断最为普遍。文献[7]基于PMSM 扩展磁链数学模型,通过建立状态观测器,重构了电机电压、反馈电流和转速观测扩展磁链,进而得到定子磁链信息。文献[8]利用龙伯格观测器与滑模观测器相结合的方法对永磁体磁链进行观测并进行失磁故障重构。文献[9]利用快速终端滑模观测器实现了对永磁体失磁故障的在线检测重构,但未考虑电机电阻、电感等因素的耦合影响。为进一步提高对磁链信息的观测精度,文献[10]针对传统方法在电阻参数发生改变时难以准确观测永磁体磁链的问题,提出了一种基于自适应非奇异终端滑模观测器的永磁体磁链观测策略,保证了磁链的观测精确度。文献[11]研究了PMSM 的失磁故障检测问题,结合自适应和滑模控制方法,提出了一种在电感扰动下估计失磁故障的自适应滑模观测器,实现了对永磁体磁链的准确估计。
上述方法均未考虑速度项对磁链观测精度的影响。为实现轨道车辆永磁牵引同步电机失磁时的精确在线检测,保障轨道车辆的高效稳定运行,本文结合滑模观测器和比例积分观测器的特点,提出了一种基于积分滑模观测器的PMSM 磁链重构方法。所设计方法消除了速度项对积分滑模观测器的动态影响,积分与滑模的结合扩展了观测器的自由度,提高了观测器的动态估计速度,并增强了对参数变化的鲁棒性。仿真结果表明,所提观测器能够实现对永磁体磁链的高精度观测。
2 系统模型
理想情况下的PMSM 在d-q坐标系下的电压方程如下[12-13]:
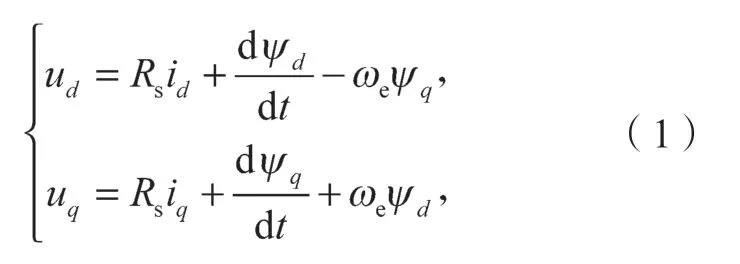
且有:
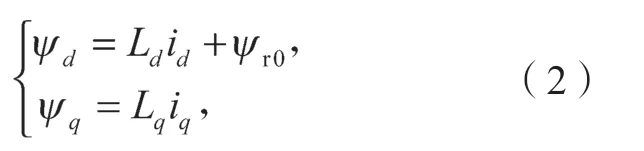
式(1)(2)中:ud(uq)、id(iq)、Ld(Lq)、ψd(ψq)分别为定子绕组d(q)轴的电压分量、电流分量、电感分量和磁链分量;ψr0为转子永磁体磁链;Rs为定子电阻;ωe为电角速度。
当PMSM 发生失磁故障时,永磁体磁链的大小和方向会发生改变,则对应式(2)的磁链方程可以重写为
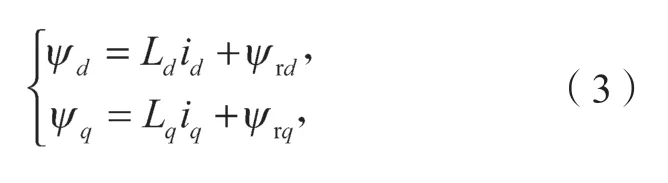
其中有:

式中:Δψrd(Δψrq)分别为d(q)轴的磁链扰动分量,且有Δψrd<0,Δψrq>0;γ为磁链偏差角,且γ∈[0°,90°) 。
由于失磁故障的影响,若按式(1)所示数学模型设计电机控制器,将使得控制器的性能与实际运行不匹配,从而导致控制性能大幅下降。为了实现电机控制器的稳定精确运行,并且能真实反映 PMSM 的运行状况,重写PMSM 在失磁故障下的d-q轴数学模型为[14]

失磁故障时,PMSM 在d-q坐标系下的电磁转矩方程为
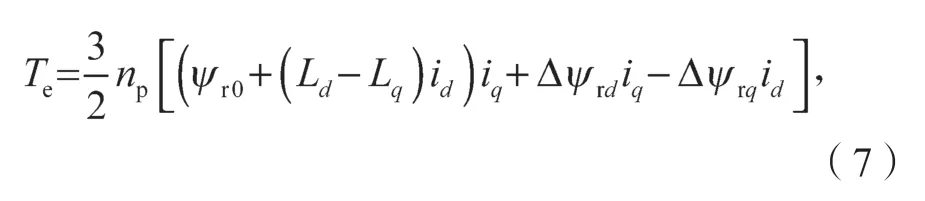
式中:Te为电磁转矩;np为电机极对数。
考虑实际的PMSM 驱动系统中,电磁系数对时间的变化率远比机械系数对时间的变化率要小,故可以认为:
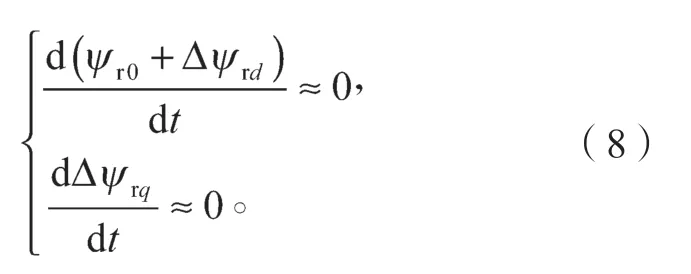
则式(6)可重写为
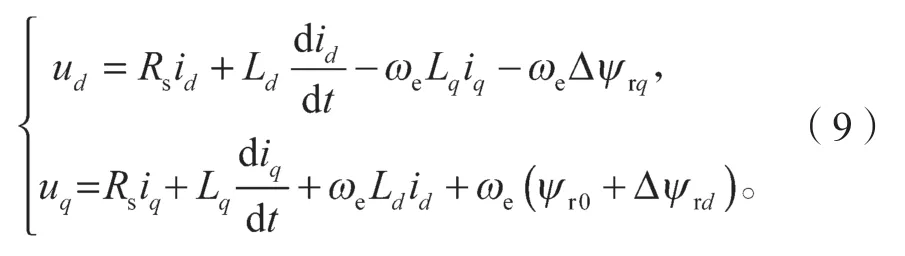
对式(9)进行以电流为状态量的变换,可列出d-q坐标系下失磁故障时永磁同步电机的电流方程为
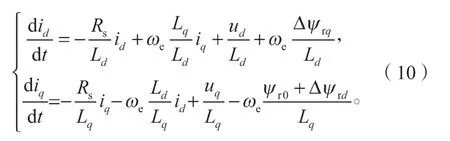

式中:x、u、f、y分别为状态变量、系统输入、失磁故障、系统输出,且定义x、u、f为
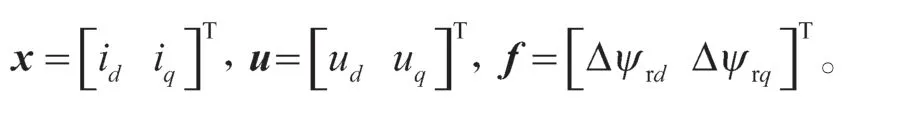
3 积分滑模控制器设计及永磁体磁链重构
3.1 积分滑模观测器设计
实际PMSM 应用中,永磁体磁链的大小是有界的,因此有常数δ,满足||f||≤δ。根据可测输入u和可测输出y,基于滑模控制原理和比例积分原理,设计积分滑模观测器实现对永磁体磁链的在线检测重构。
结合SMO 的设计原理和比例积分观测器的突出特点,插入一个解耦系数ωe和积分项,并保留滑模项v,得到积分滑模观测器表达式为
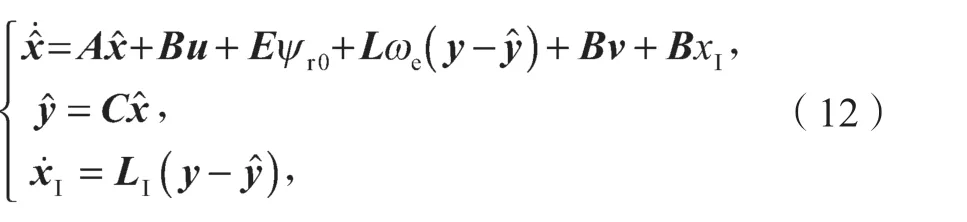
所设计观测器的方框图见图1。

图1 观测器方框图Fig.1 Block diagram of the observer
选取滑模面为
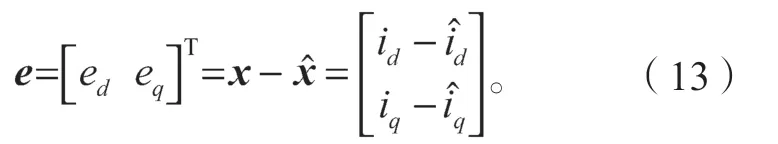
对误差e求导可得:
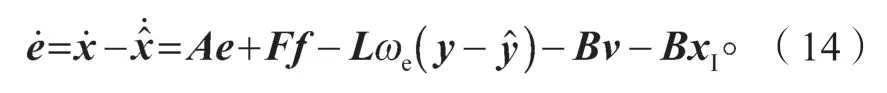
综合考虑滑模收敛速度及观测器观测精度,选取合适的参数K、L和LI,导数在有限的时间内便可趋近于0。
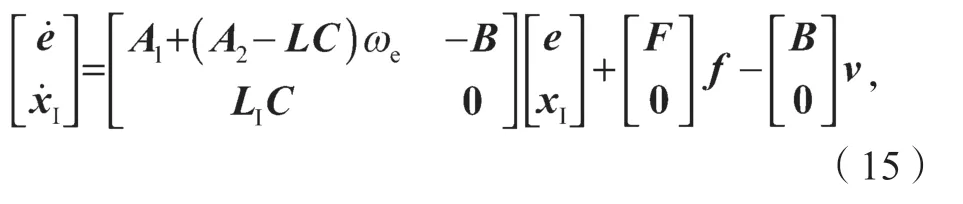
式中存在:

其中有:
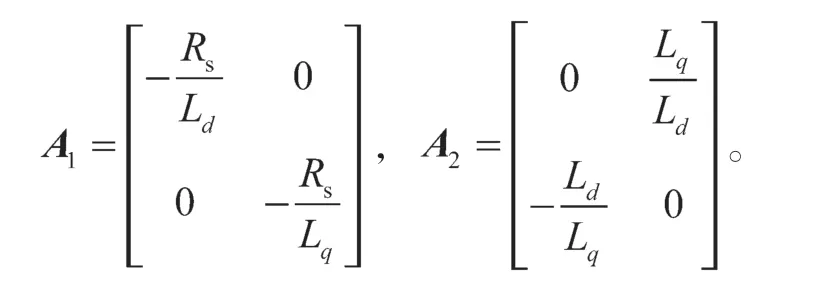
令

可以得到:

由此可以得到:
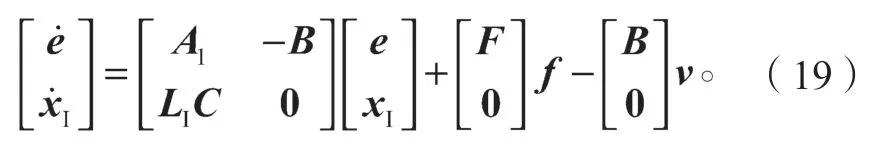
通过对积分观测器给出的误差状态方程系数矩阵的对比观察可知,若按式(18)选择L的取值大小,则积分SMO 的误差状态方程系数矩阵中只含有A1,通过对A1的定义可知,其为一个常数,不含电角速度ωe,这就消除了ωe对积分滑模观测器的动态影响,提高了积分SMO 的动态观测性能。同时,积分SMO 融合了SMO 和比例积分观测器两者的优势,保留了积分项xI和滑模项v。积分项xI使得积分SMO 拥有和比例积分观测器一致的二阶自由度,提高了积分SMO 的动态估计速度;滑模项v的保留则增强了积分SMO 对参数变化的不灵敏性,增强了系统的鲁棒性。
3.2 积分滑模观测器稳定性分析
定理1存在小的正常数η和ζ满足
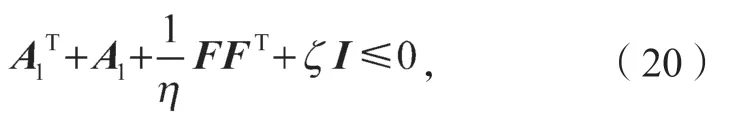
式中I为单位矩阵。
恰当选取增益LI和K的取值,则式(19)所示的积分滑模观测器误差在有限时间收敛并最终稳定。
选择Lyapunov 函数为

对其求导得:
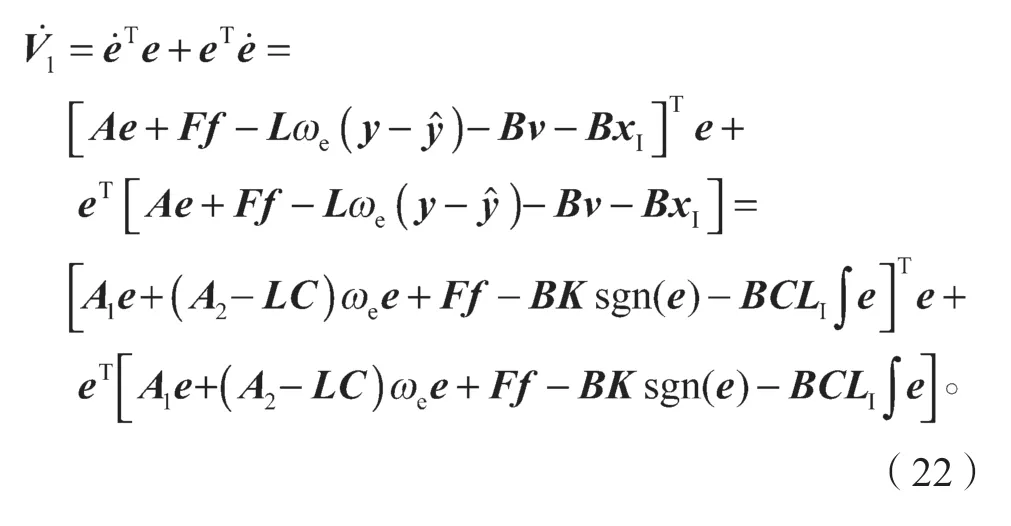
将式(18)代入式(22)可得:
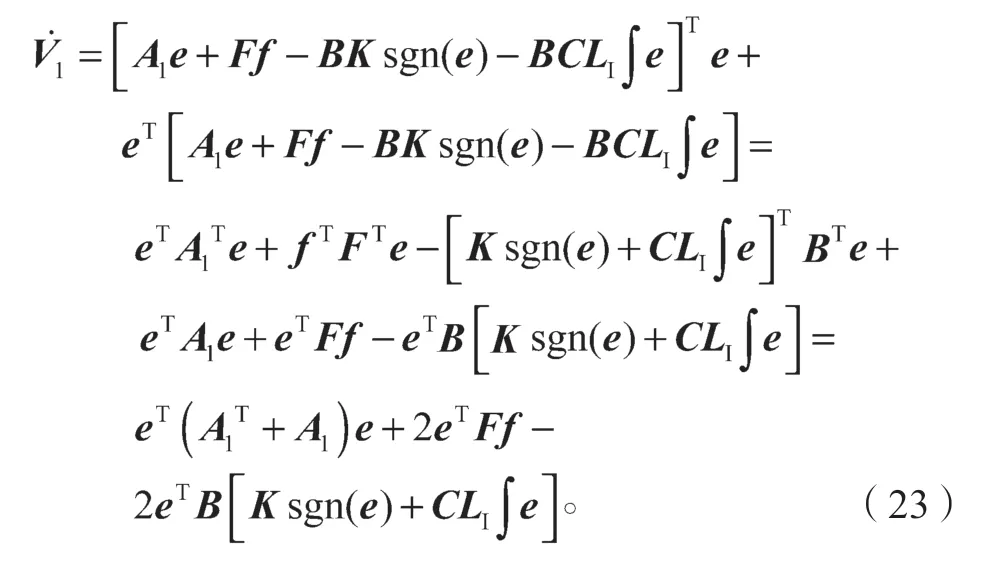
根据杨不等式定理[15],给定一个小的正常数η满足下式:
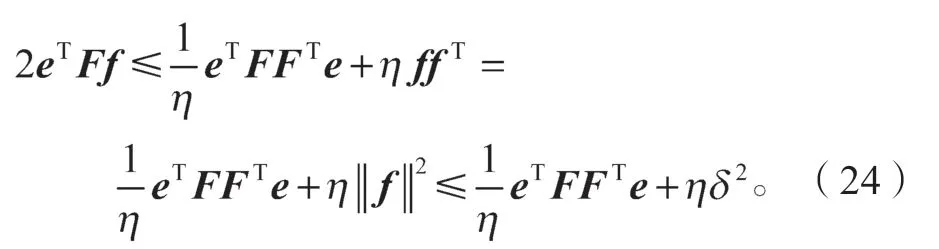
根据式(24)和(20),可以得到:
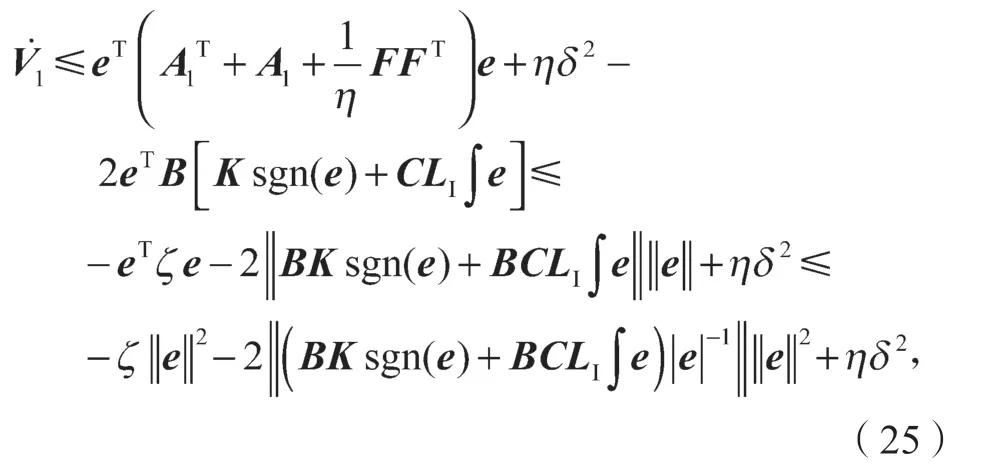
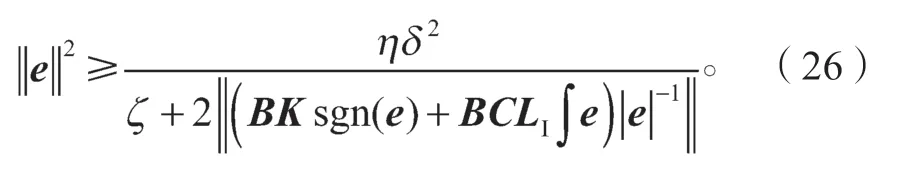
因此,通过Lyapunov 稳定性判据,式(19)所设计的积分滑模观测器误差能在有限时间内收敛。这就完成了对观测器稳定性证明。
3.3 永磁体磁链重构
当系统状态接近滑模面e后,由滑模等值原理[16],有,代入式(14)得到:
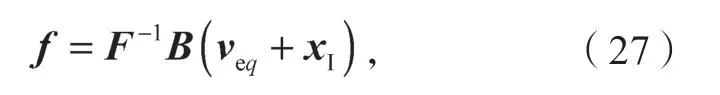
式中,veq是滑模项v的一个等价输出量。
由式(27)可得永磁体磁链在d-q坐标系下的磁链扰动分量的估计表达式为

为了改善由于滑模项的不连续性带来的大抖振现象,此处以具有连续特性的θ(s)函数来取代具有不连续特性的sgn(s)函数,以达到对抖振现象的有效消除[16]。故可以将PMSM 失磁故障时的重构算法重写为式(29)。

式中,ε1和ε2均为大于0 的常数。
重构后的转子永磁体在d-q轴的磁链分量和为
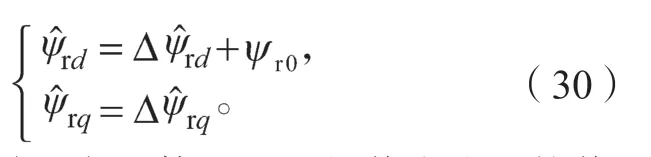

同理,可得到失磁故障时转子永磁体磁链和d轴之间的估计偏差角重构值为
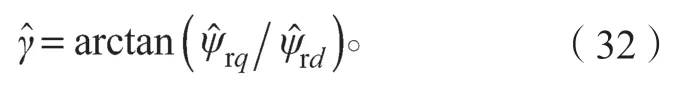
4 系统仿真分析
采用Matlab-Simulink 仿真对所提出的基于积分滑模观测器的磁链重构算法进行可行性分析和精确性验证,所用的电机具体参数及取值见表1。

表1 PMSM 参数与取值Table 1 PMSM parameters and values
基于积分滑模观测器的永磁同步电机转速控制框图如图2所示。
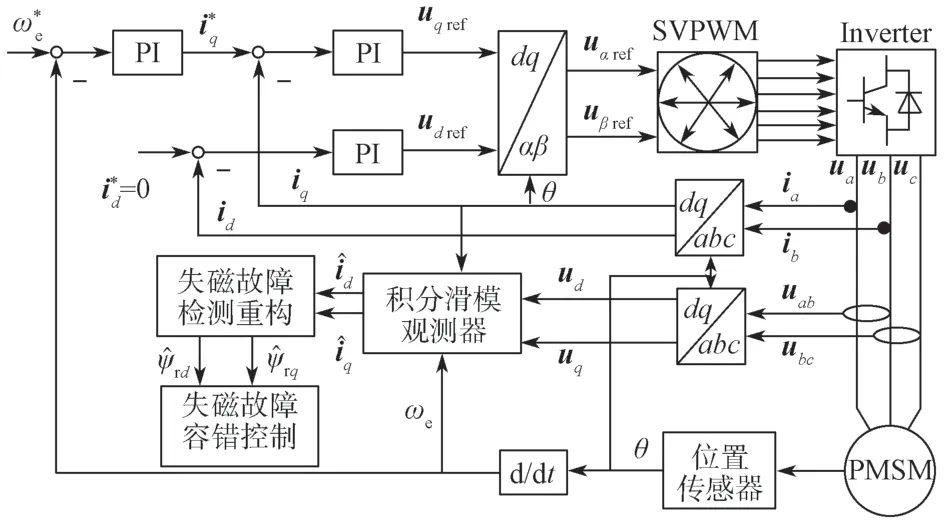
图2 基于积分滑模观测器的PMSM 转速闭环控制框图Fig.2 Block diagram of closed-loop speed control of PMSM based on integral sliding mode observers
如图2所示,该转速闭环系统主要包含了速度、电流PI 控制器、位置和速度检测、积分滑模观测器和失磁故障检测重构等模块。
采用id=0 的控制策略。根据上述推导的稳定性条件,设置k1=k2=30,LI1=LI2=10,ε1=ε2=0.01。由式(18)得到L的取值为
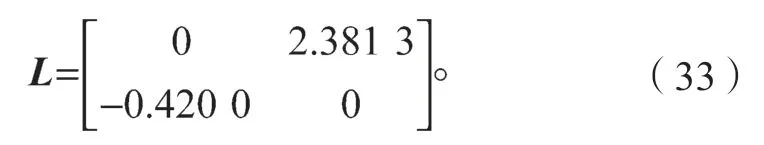
4.1 正常运行下的仿真结果分析
在电机正常运行情况下,电机带载起动,设置初始转速和给定转矩分别为100 r/min 和100 N·m。图3~5 分别给出了永磁同步电机在正常情况下转速跟踪情况、永磁体磁链跟踪情况和d-q轴电流跟踪情况的仿真结果。

图3 正常运行时的转速实际值与参考值Fig.3 Actual speed and reference values under normal operative conditions
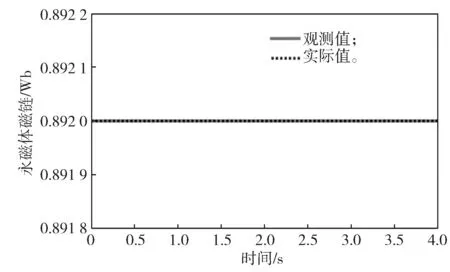
图4 正常运行时的永磁体磁链实际值与观测值Fig.4 Actual and observed values of PM flux linkage under normal operative conditions
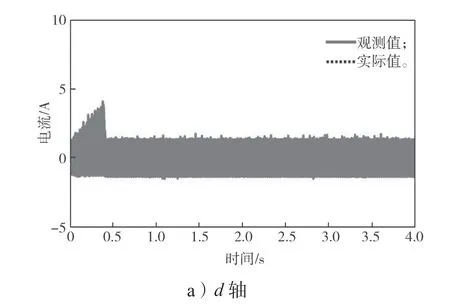
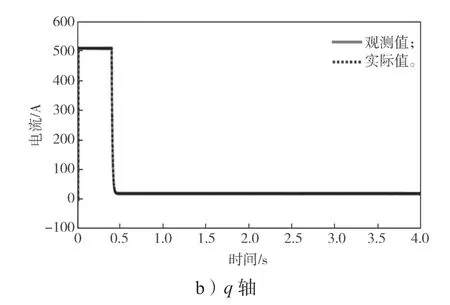
图5 正常运行时的 d-q 轴电流实际值与观测值Fig.5 Actual and observed values of d-q axis current under normal operative conditions
从图3~5 可以看出,在正常运行情况下,电机实际转速能够快速精确地跟踪其参考值,d-q轴电流观测值能快速精确地跟踪其实际值,从而使得磁链观测值能够准确跟踪上其实际值。
4.2 失磁时的仿真结果分析
在失磁情况下,电机带载起动,设置初始转速为100 r/min,给定转矩为100 N·m。在1 s 时设置ψr减小为0.7ψr,2 s 时设置ψr减小为0.5ψr,3 s 时设置ψr减小为0.3ψr;同时,在1 s 时设置γ为30°,2 s 时设置γ为45°,3 s 时设置γ为60°。
图6~10 分别给出了永磁同步电机在同时发生幅值和角度失磁故障时,d-q轴电流、d轴磁链扰动分量、永磁体总磁链、d-q轴磁链分量和磁链偏差角的仿真结果。

图6 失磁时d-q 轴电流实际值与观测值Fig.6 Actual value and observed values of d-q axis current during demagnetization
从图6可以看出,当永磁体在1,2 ,3 s 处同时发生幅值失磁和角度失磁时,d轴电流维持在0 A 左右,q轴电流在1,2 ,3 s 处相应增大。
从图7~10 可以看出,当电机同时发生幅值失磁和角度失磁时,q轴磁链分量在1 s 和2 s 时增大,而在3 s 时减小;d轴磁链分量在相应时刻均减小,但在3 s 时存在一个小的波动,但其观测值也能迅速跟踪其实际值。d轴磁链分量在3 s 时的波动也导致总磁链幅值的观测值和磁链偏差角的观测值在3 s 时也产生了短时间的跟踪偏差,但其均能快速准确跟踪上实际值。
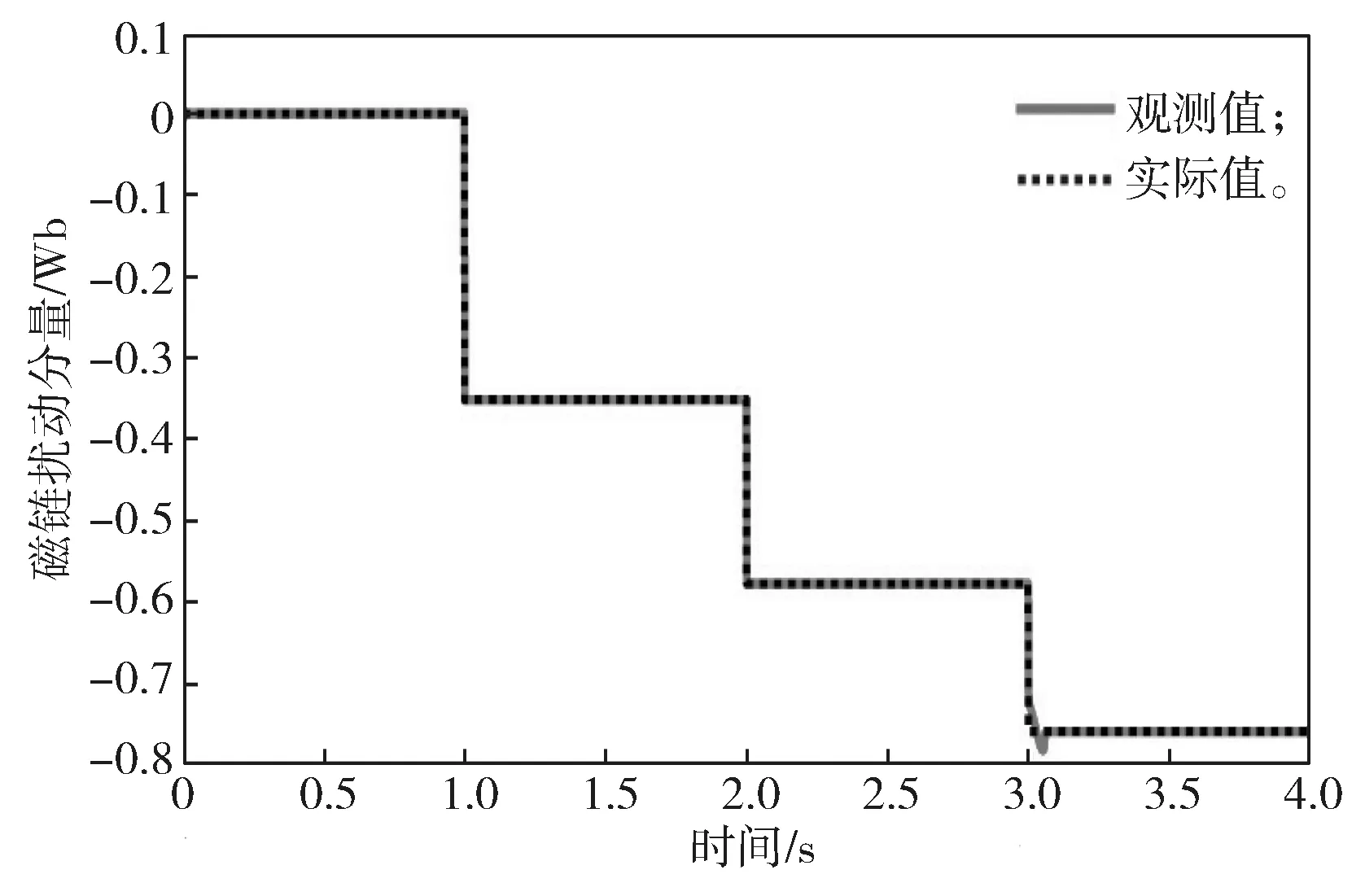
图7 失磁时d 轴磁链扰动分量实际值与观测值跟踪结果Fig.7 Tracking of the actual and the observed values of the d-axis flux linkage disturbance component during demagnetization
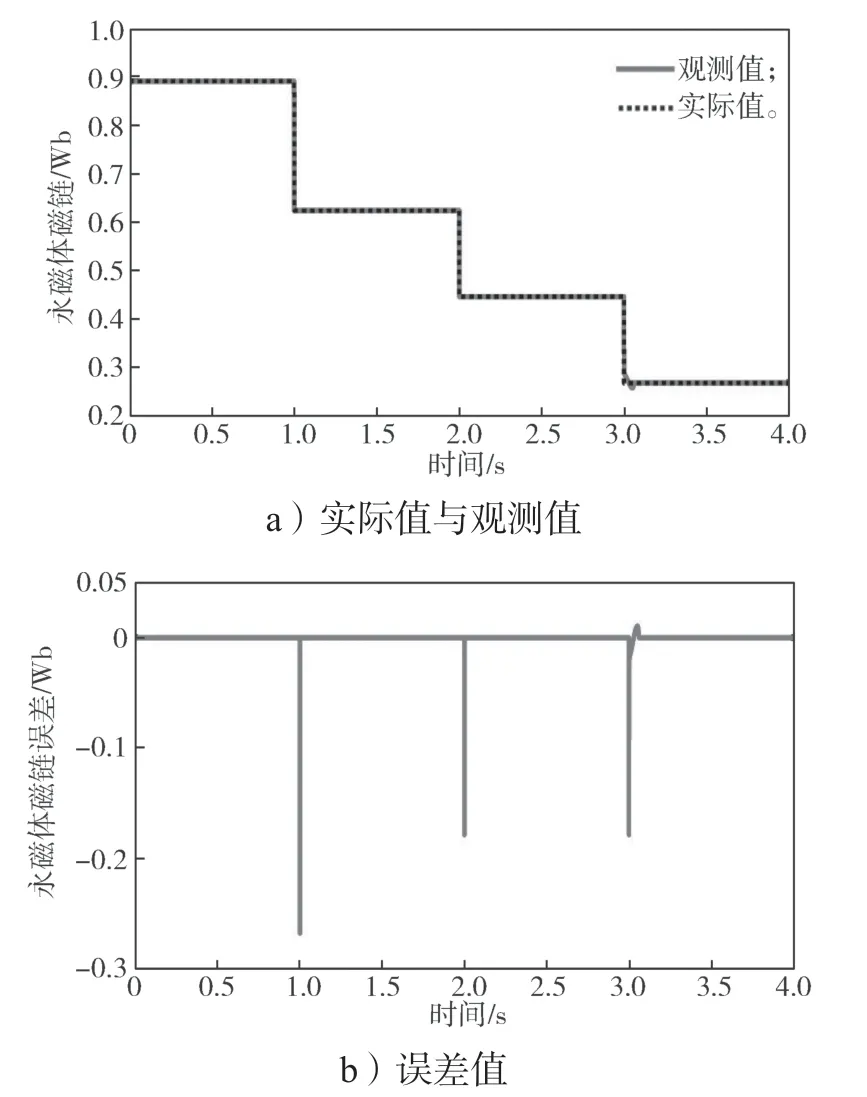
图8 失磁时磁链实际值与观测值及其误差曲线Fig.8 Actual and observation values of flux linkage with their errors during demagnetization
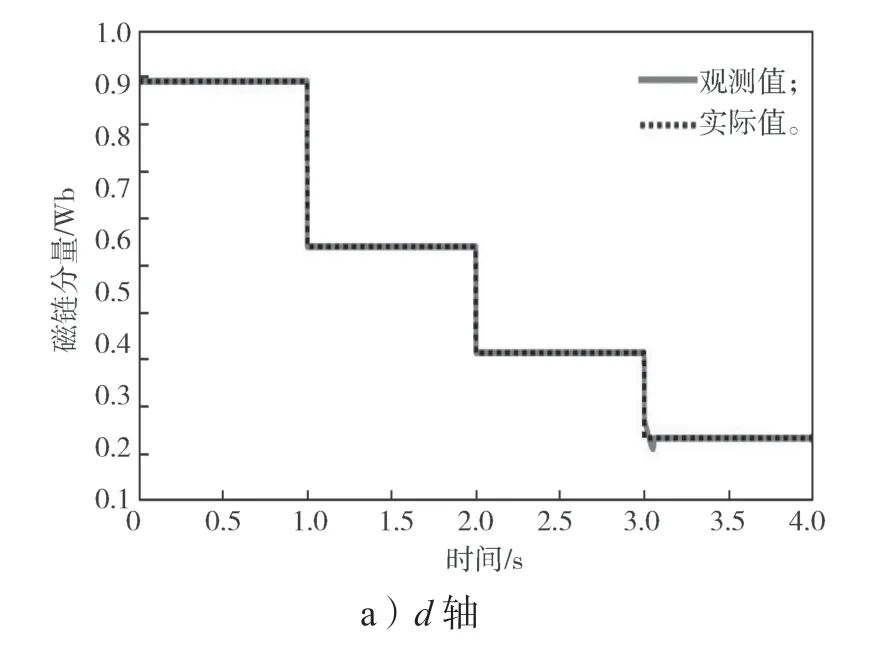
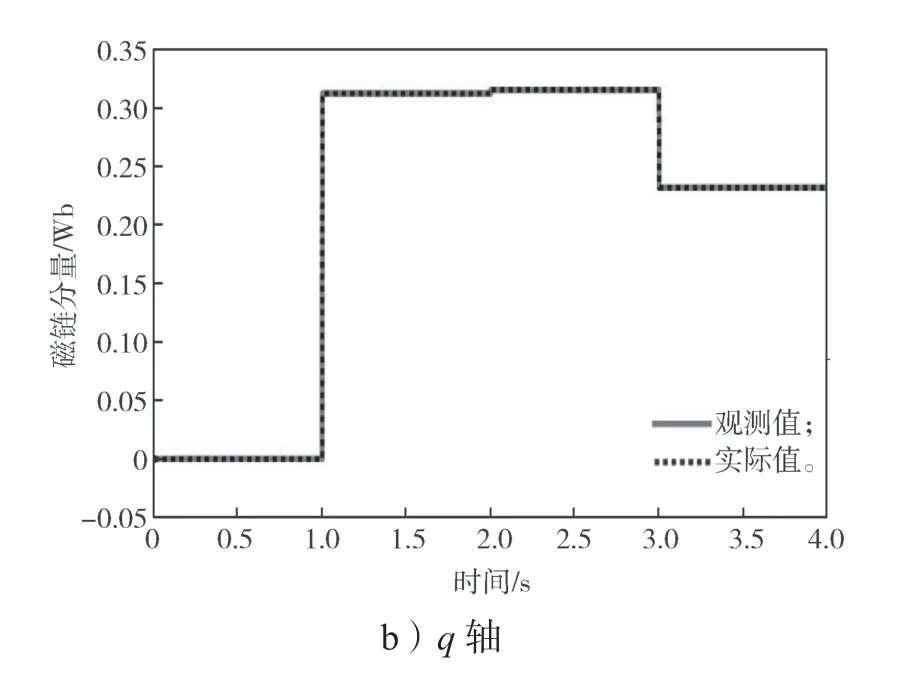
图9 失磁时d-q 轴磁链分量实际值与观测值Fig.9 Actual and observed values of d-q axis flux linkage components during demagnetization
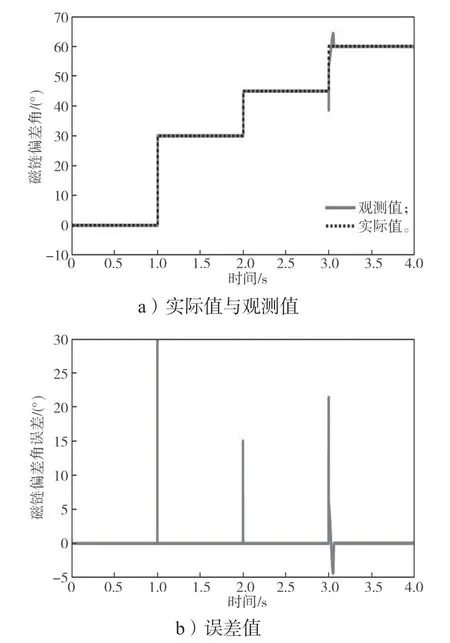
图10 失磁时磁链偏差角实际值与观测值及其误差跟踪曲线Fig.10 Actual and observed values of flux linkage deviation angle with their error tracking during demagnetization
从上述仿真结果可知,d-q轴电流、永磁体磁链大小和磁链偏差角及d-q轴磁链分量的观测值都能够准确快速跟踪其实际值,这充分表明所设计的积分滑模观测器可快速准确收敛到永磁体磁链的幅值和方向,实现了对永磁体磁链的在线检测和重构。
5 结语
本文以永磁同步电机转子永磁体为研究对象,提出了一种基于积分滑模观测器的永磁同步电机磁链重构方法。通过建立d-q坐标系下的电机失磁故障数学模型,选择定子电流作为系统状态变量,通过加入解耦项和积分项构建了积分滑模观测器,实现了对永磁体磁链的重构与在线检测。仿真结果表明,所提出的积分滑模观测器能够对永磁体磁链进行快速精确地观测辨识,验证了基于积分滑模观测器的磁链重构方法的准确性和有效性。后续将开展在永磁同步电机负载以及参数变化时的磁链重构及其容错控制方面的研究。

