基于理正岩土计算和ANSYS的某重力式挡土墙结构分析

唐 杨，王国炜，亓兴军，赵 涛

（1.五峰土家族自治县农村公路管理所，湖北 宜昌 443413；2.山东金衢设计咨询集团有限公司，山东 济南 250014；3.山东建筑大学 交通工程学院，山东 济南 250101；4.济南市规划设计研究院，山东 济南 250101）

0 引言

挡土墙作为重要的防护工程构造物，在公路、铁路、水利等工程中应用广泛[1-4]，因此，各种新型结构形式的挡土墙发展迅速，逐渐进入大众视野。而重力式挡土墙作为最传统的结构形式，在实际工程中扮演着重要角色，因此学者们对重力式挡土墙进行了大量的研究[5-8]。

实际工程项目中，挡土墙在复杂的地质状况以及多种荷载工况下遭受破坏的工程案例不胜枚举，因此，为保证施工质量，需要对传统的重力式挡土墙进行严格的结构分析，以确保其结构受力和结构稳定性满足规范要求。同时，随着人工、材料、机械价格的上涨，挡土墙的工程造价越来越高，其结构分析和优化设计研究的重要性受到众多专家学者的关注。李刚等[9]针对某城市防洪土建工程衡重式挡土墙，通过现场检测以及有限元建模计算分析，发现墙身与衡台连接处存在拉应力区，当墙后土侧压力过大或者墙身结构强度不足时，墙身易产生开裂，进而影响挡土墙的整体稳定性。王青等[10]为优化挡土墙稳定性，设计了一种UHPC-CA装配式干砌挡土墙，利用试验、有限元仿真和理论分析等手段对其稳定性进行研究，结果表明该新型挡土墙整体性良好，抗倾覆安全稳定性可达到等同现浇的效果。F.Bari 等[11]通过计算石质重力式挡土墙的外部和内部稳定性，对重力式挡土墙的最佳高度进行研究，结果表明重力式挡土墙在14 m 内的外部稳定性符合安全要求，但是其内部稳定性分析在高度为8 m 时就不再符合安全要求，故重力式挡土墙的最佳高度为7 m。吴凯等[12]利用块石和混凝土两种材料，组合成一种新型的重力式挡土墙，但该研究只有片面性的说明，缺乏充分的计算论证；倪世权[13]分析了影响航道护岸重力式挡土墙滑移稳定性的各种原因，但针对此类具有航道护岸特点的重力式挡土墙计算分析却很少。

综合挡土墙的研究成果发现，目前对挡土墙的结构分析仍然较少，且大部分为较为浅显的说明性分析成果。并且，近年来重力式挡土墙被破坏事件时有发生，而针对重力式挡土墙的破坏大都缺乏定量的结构计算，一般只是针对工程经验并结合现场的破坏情况进行定性分析，进而采取相应的处置措施[14-15]；针对重力式挡土墙加固效果的计算分析同样较少。

本文将以某项目中的重力式挡土墙为工程背景，采用理正岩土计算程序对挡土墙的基本受力状态进行验算，然后利用ANSYS 有限元分析软件建立数值模型进行计算分析，以期全面掌握本项目挡土墙的受力情况，为项目顺利实施提供理论参考依据。

1 工程概况

项目中重力式挡土墙高6.7 m，顶部宽0.6 m，底部宽2.0 m，墙前埋置深度为2.5 m，墙背坡率为1:0.24，墙面坡率为1:0.5，混凝土采用C30 商品混凝土，挡土墙几何尺寸如图1所示，图中尺寸单位为cm。

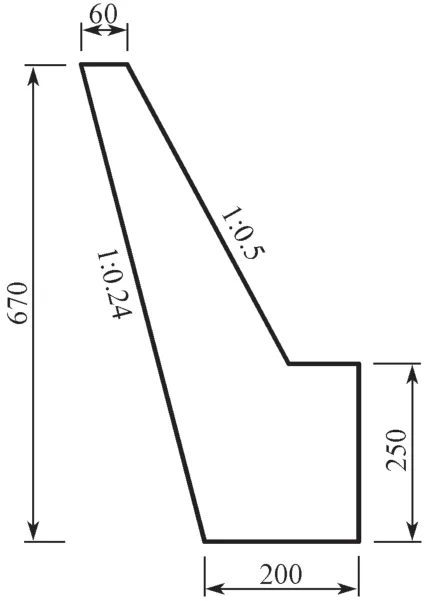
图1 重力式挡土墙几何尺寸示意图Fig.1 Schematic diagram of geometry dimensions of the gravity retaining wall

为了较为准确地分析重力式挡土墙的受力状态，采取一个较大土体范围进行建模分析，即在墙前考虑12 m 的土体，墙后除了1:1.634 的边坡以外，考虑12 m 的土体，地基土考虑12 m 深度范围，具体的数值分析范围如图2所示。

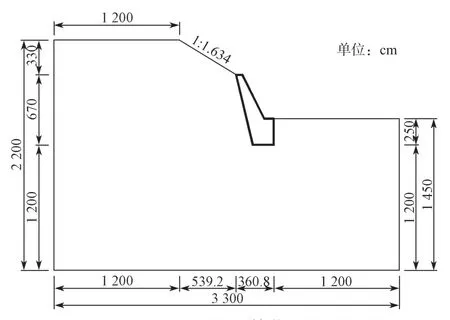
图2 土体计算范围Fig.2 Soil mass calculation range

2 理正岩土计算软件验算

2.1 思路分析

结构验算采用理正岩土计算6.5PB3 版，验算前需要在程序中输入重力式挡土墙的墙身尺寸、坡线土柱物理参数等计算参数。

在坡线土柱设置页面，坡面线段数设置为2，输入墙后的两段坡面线，坡面起始距离设置为0，地面横坡角度设置为0，填土对横坡面的摩擦角设置为30°；由于不考虑车辆荷载，换算土柱设置为0；由于墙前填土深度为2.5 m，故而在墙前添加附加集中力，通过输入墙前填土深度和土体参数，计算得到墙前荷载为164.07 kN/m。在物理参数设置页面，设置的具体物理参数见表1。在基础设置页面，基础设置为天然地基。在整体稳定性设置页面，稳定计算容许安全系数设置为1.25，并设置以墙面顶点为圆心，10 m 为半径的圆弧为计算滑动面。

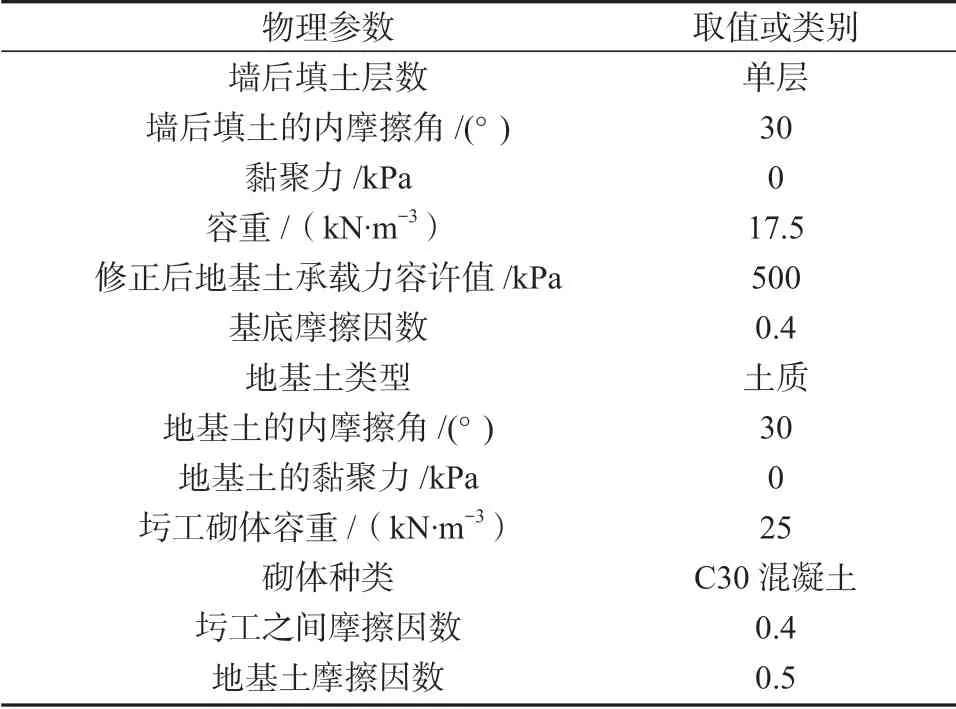
表1 物理参数表Table 1 Physical parameter table

2.2 验算结果

经过理正岩土计算程序验算分析，得到的验算结果见表2，表中数据表明挡土墙的抗滑稳定性、抗倾覆稳定性、地基承载力、截面应力、整体稳定性等受力指标均满足相关规范和设计手册[16-17]要求。

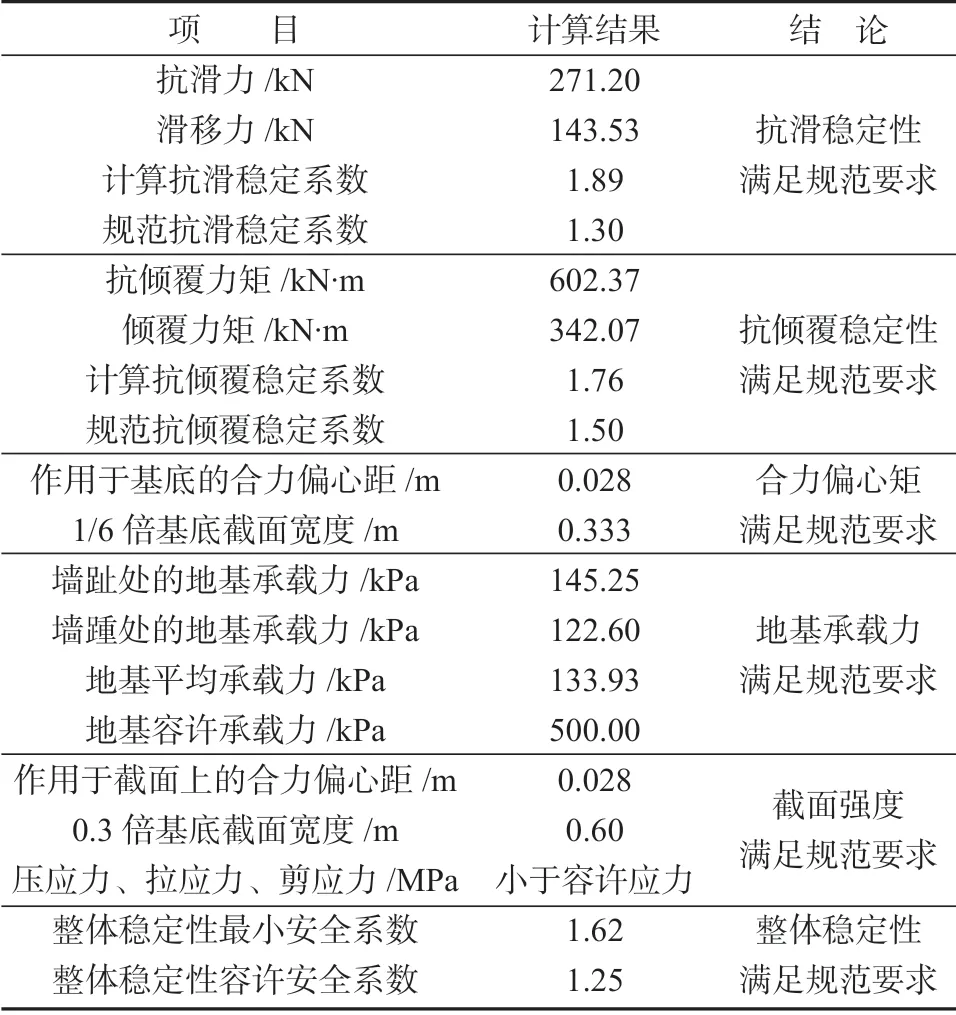
表2 理正岩土计算验算结果Table 2 Checking calculation results of normalized geotechical calculation

3 ANSYS 模型分析

3.1 思路分析

根据弹性力学理论，重力式挡土墙仅承受横向作用力，故纵向应变可视为0，符合平面应变的条件假设，为了简化分析难度，采用平面应变模型代替空间实体模型。

3.2 有限元模型构建

对模型的计算分析采用ANSYS 18.0。重力式挡土墙和土体采用Plane82 单元模拟，同时采用Targe169 和Conta172 单元作为重力式挡土墙和土体的接触单元，重力式挡土墙与土体之间的摩擦因数设置为0.4。重力式挡土墙采用线弹性模型，其抗拉强度设计值为1.39 MPa，抗压强度设计值为13.8 MPa，土体采用DP 模型，其材料力学特性见表3。计算中仅考虑自重荷载，施加重力加速度g（g取9.8 m/s2）。在边界条件上，约束土体两侧边界的水平位移和土体底部边界的竖向位移。

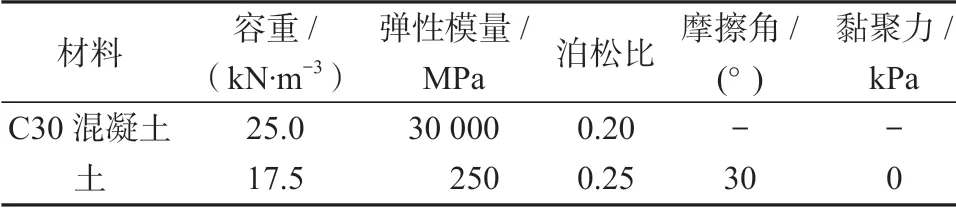
表3 挡土墙的材料力学特性表Table 3 Table of material mechanical properties

采用映射网格技术划分网格，得到的有限元模型如图3所示，计算分析中的单位制采用N、m、Pa。

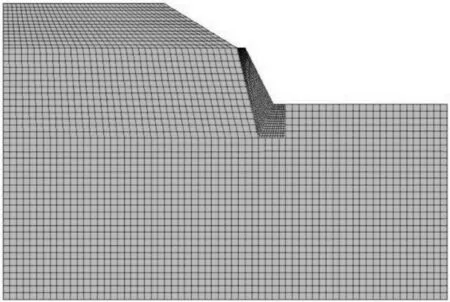
图3 重力式挡土墙的有限元分析模型Fig.3 Finite element analysis model of the gravity retaining wall

3.3 结果分析

通过ANSYS 结果计算分析，得到计算范围内的整体位移如图4所示，重力式挡土墙的位移云图5所示，重力式挡土墙的应力云图如图6所示。

图4 计算范围内的整体位移云图Fig.4 Overall displacement pictures of the calculation range

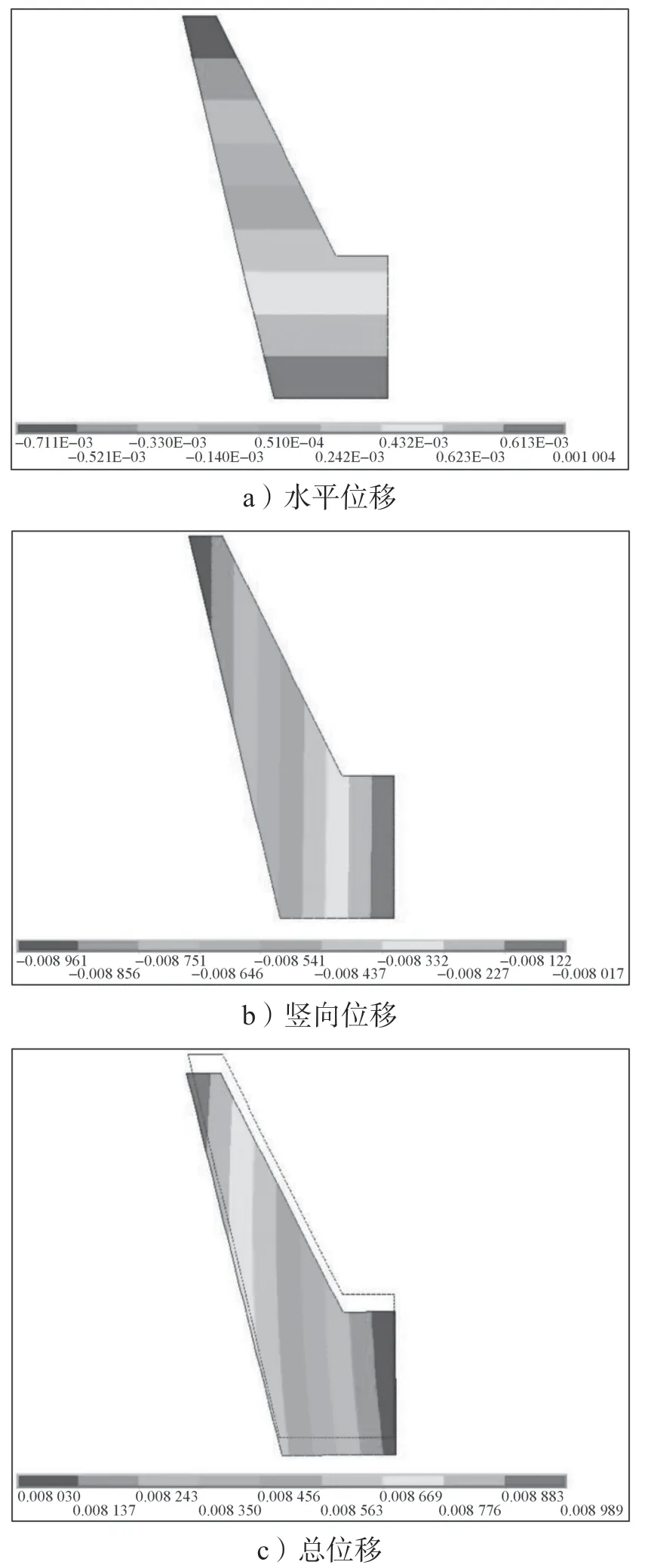
图5 重力式挡土墙的位移云图Fig.5 Displacement pictures of the gravity retaining wall

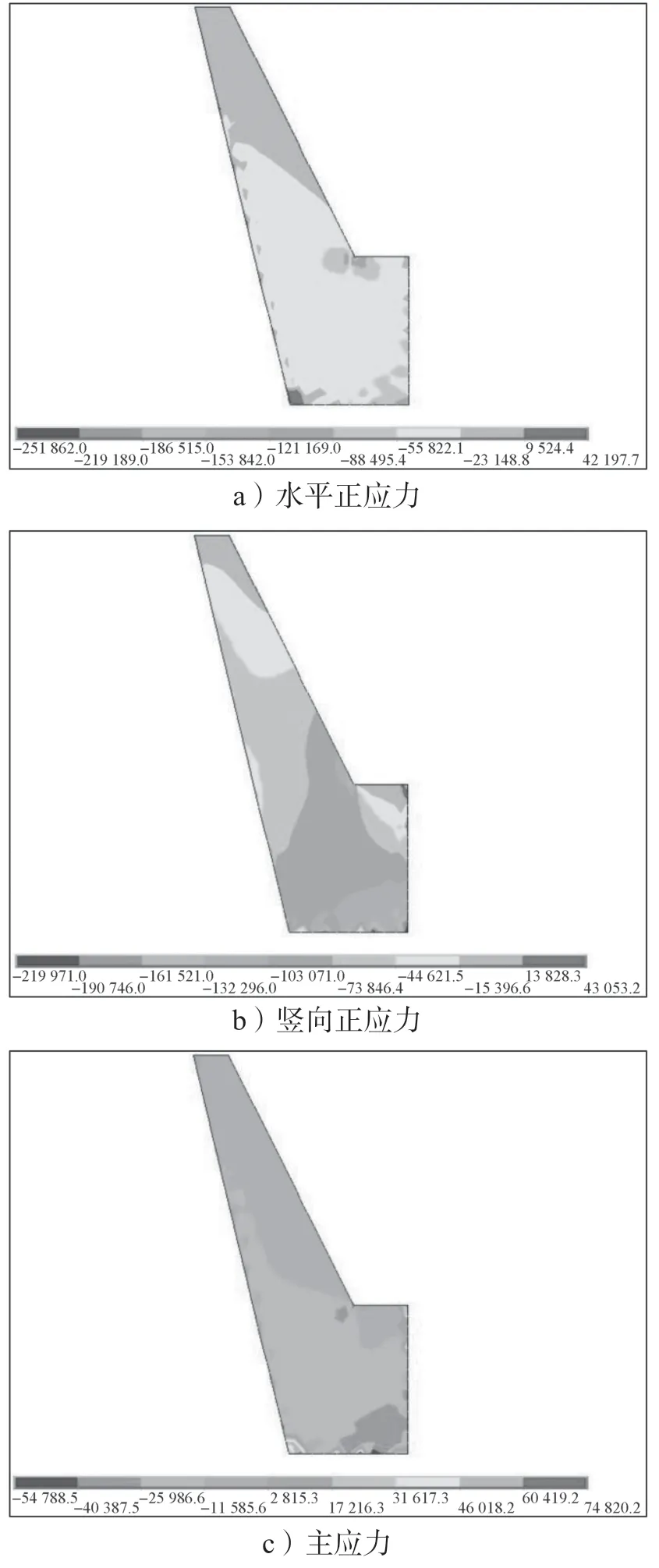
图6 重力式挡土墙的应力云图Fig.6 Stress pictures of the gravity retaining wall

由图4a 可以看出，计算范围内的正向水平位移最大值出现在重力式挡土墙的底部土层附近，约为1.05 mm；负向水平位移最大值出现在重力式挡土墙墙后的坡顶位置，即坡面线发生变化的位置，约为0.94 mm。由图4b 可以看出，计算范围内均为负向竖向位移，其负向竖向位移最大值出现在坡顶的水平段，约为14.44 mm。由图4c 可以看出，计算范围内的最大位移在墙后填土的水平坡段，其位移最大值约为14.44 mm；最小位移在土体底层，其位移最小值为0。综合来看，计算范围内的位移主要表现为竖向位移，水平位移相比于竖向位移可以忽略不计。

由图5a 可看出，重力式挡土墙的水平正向位移最大值出现在基础底部，约为1.00 mm，水平负向位移最大值出现在重力式挡土墙的顶部，约为0.71 mm，由此可见，重力式挡土墙存在向土体内侧倾斜的变化趋势；由图5b 可看出，负向竖向位移最大值发生在重力式挡土墙顶部，约为8.96 mm，负向竖向位移最小值发生在基础墙面上，约为8.02 mm；由图5c 可看出，重力式挡土墙的总位移最大值为8.99 mm，出现在重力式挡土墙顶部，最小值与最大值相比较为接近，约为8.03 mm，出现在基础墙面上。

由图6a 可看出，重力式挡土墙的水平拉应力最大值出现在墙趾位置，约为0.42 MPa，水平压应力最大值出现在墙身与基础的夹角位置，约为2.52 MPa；由图6b 可看出，重力式挡土墙的竖向拉应力最大值出现在基础位置墙面一侧的顶部，约为0.43 MPa，竖向压应力最大值出现在基础底部，约为2.20 MPa；由图6c 可以看出，重力式挡土墙的主拉应力和主压应力最大值均出现在基础底部，主拉应力最大值为0.75 MPa，主压应力最大值为0.55 MPa。综合以上应力分析可知，重力式挡土墙的主应力在C30混凝土抗拉和抗压强度设计值内。

4 结论

本文以项目中的重力式挡土墙为实例，通过理正岩土计算程序进行结构验算分析和ANSYS 有限元的精细化结构分析，得到以下结论：

1）理正岩土计算程序的分析结果表明，重力式挡土墙的稳定性、地基承载力、截面应力均能满足结构受力要求。

2）ANSYS 精细化有限元分析结果表明，重力式挡土墙的竖向位移远大于水平位移，墙后填土的水平段沉降较大；从重力式挡土墙的结构位移和结构应力综合分析，重力式挡土墙的结构变形较小，主要表现为刚体位移，其主拉应力距离C30 混凝土的抗拉强度设计值较远，具有足够的拉应力储备，主拉应力主要出现在基础底部和墙面一侧。

3）综合理正岩土软件验算分析和ANSYS 精细化有限元分析，由于墙前填土极易遭受破坏，建议在重力式挡土墙的基础底部设置防滑凸榫或者墙底倾斜坡度，从而提高重力式挡土墙的抗滑稳定性和抗倾覆稳定性。