竖直式太阳能烟囱对大空间自然通风的增益模拟
姚奕合,赵福云,2,谭志成,陈 皓
(1.湖南工业大学 土木工程学院,湖南 株洲 412007;2.武汉大学 动力与机械工程学院,湖北 武汉 430072)
0 引言
随着“双碳”目标的提出,节能减排在我国已是必行之路,如何将能耗与碳排放降低,成为各级政府与企业眼中的重大难题。太阳能烟囱是一项通过自然光照,在烟囱内部壁面蓄热,从而更改室内外空气密度,增益自然通风的环保技术。较多科研工作者对此进行了研究。如任秀宏[1]在烟囱内部设立离散热源以改善烟囱内气流回流情况。姚丽萍等[2]总结了不同瑞利数下,烟囱内部出口质量流量随烟囱高宽比的变化规律。唐明远[3]考虑了不同烟囱进风口尺寸对烟囱内部流场的影响。端木祥铃[4]通过盐水实验,对3 种不同形式的烟囱,比较了不同烟囱结构参数对太阳能烟囱通风量的影响。赵平歌[5]通过加热不同的烟囱壁面,选用不同开口方式,探究了其对通风量的影响。D.J.Harris[6]、Chen Z.D.[7]等通过改变太阳能烟囱倾斜角度,并对比不同角度下的烟囱内部气流流量,得出了烟囱的最佳倾斜角度。J.Arce 等[8]选取trombe 式太阳能烟囱,在不同蓄热墙体、不同热流密度情况下,提取不同高度空气龄,得出最佳热流密度范围。R.Khanal 等[9]针对此类被动式建筑通风,综述了各类文献,发现已有研究主要为太阳能烟囱的几何形状、倾斜角及壁面热流密度等方面。
国内外学者针对太阳能烟囱技术的已有研究,主要以太阳能烟囱几何模型、壁面热流密度为参照变量,分析太阳能烟囱内部流场的相关特性,但并未关注此类技术运用后,室内气流流动情况。因此,本文拟对运用太阳能烟囱技术的情况下,拓展数值计算域,模拟自然通风在各个开口处较真实的风速与风向,分析建筑内部流体的流动情况,并使用空气龄评价指标结合流体流速分析,以选取最佳的被动式建筑通风自由开口位置、太阳能烟囱高宽比,以期为低能耗建筑技术提供对比与参考。
1 数值计算与理论分析模型
1.1 物理模型
本文在二维情况下,将模型设计为外部拓展域与内部模型两部分。由于简单地讨论热压或风压对于自然通风的影响,并不能有效地模拟出实际结果,为了考虑完全自然通风的相关情况,本文参照文献[10]进行了拓展域设计。模型的外部拓展域示意图见图1,图中H为模型高度。

图1 模型外部拓展域示意图Fig.1 Schematic diagram of the external expansion domain of the model
内部模型参照大空间厂房的特点设置,模型长为L,高为H,且L=2H;烟囱设立在厂房中部,其固定高Hc为0.2H,宽度为B;厂房内设置集中线热源,其长度Lh为0.25H。在厂房两侧壁面中部,设立通风口,宽度为0.1H。以穿堂风式自然通风开口为例,其内部模型如图2所示。

图2 内部厂房模型示意图Fig.2 Schematic diagram of the internal plant layout model
1.2 数学模型
1.2.1 湍流模型
本研究选用计算流体动力学(computational fluid dynamics,CFD)模拟方法,并采用ANSYS 软件中的ICEM CFD 进行相关模型的建立及网格划分,然后导入fluent 软件中进行具体计算。
由于本模型具大空间厂房的特点,故选用Realizeblek-epsilon 湍流模型。该模型因考虑了旋转与曲率,故在能量转换上与计算收敛方面有很好的适应性。其控制方程包括连续性方程、能量守恒方程、动量守恒方程、湍流动能方程以及耗散率方程,相应的计算公式具体如下。
1)连续性方程。其表达式为

式中:ρ为密度;Ui为i方向上的速度;xi为具体方向。
2)动量守恒方程。其表达式为

式中:Uj为j方向的速度;Fi为i方向的力;p为静压;μ为修正系数。
3)能量守恒方程。其表达式为

式中:h为高度;λ为相应参数;cp为空气中的比热容;SH为显热。
4)湍流动能方程。其表达式为

式中:K为湍流动能;Re为雷诺数;Vt为黏度;σk为参考系数;ε为耗散率;Xi为具体方向坐标,P为压力;G为重力。
5)湍流动能耗散率方程。
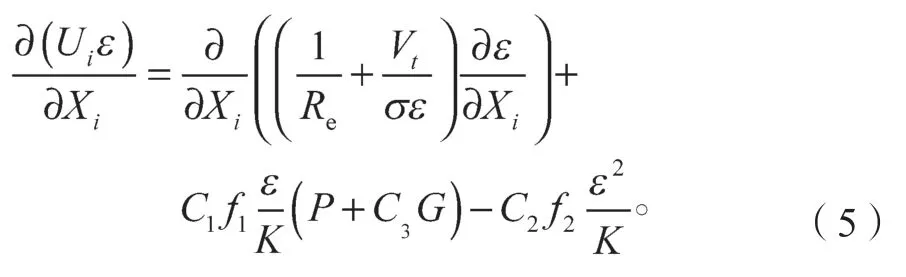
式中:σ为参考系数;Ci为常数;fi为i方向上的力。
1.2.2 辐射模型
为了简化计算,本研究忽略模型中的空气散射。针对模型内壁面存在热流密度、辐射以及模型内部具有局部热源的情况,采用DO 辐射模型较为合理[11]。
1.2.3 材料物性与边界条件
采用boussinesq 假设,加强模型的收敛性,并打开热浮升,以加强壁面热效应。设置厂房内部壁面两通风口及烟囱上部为interior 边界。选用定温定压铝制壁面热源,温度为500 K,密度为2 719 kg/m3。烟囱壁面两侧皆设置玻璃壁面,其热壁面吸收率为0.95,密度为2 220 kg/m3,相应温度变化由壁面的热流密度值决定。其余内部壁面为定温混凝土结构,其密度为2 500 kg/m3。在拓展域左侧设置由velocity-inlet 定义的梯度风,其温度为290 K,密度为1.177 kg/m3,右侧为outflow,上部边界条件为symmetry。
梯度风相应公式如下:

式中:U(Y)为水平风速,m/s;Y为高度,m;UH为在α条件下的静风速度,m/s(α=0.35,UH=2)。
1.2.4 模型验证
本模拟模型参考相关文献,并依据相应条件做出调整,计算了不同壁面热流密度在不同太阳能烟囱宽度下,太阳能烟囱内的自然通风量,且对比文献[12]中相应的数据进行验证。
由公式(7)可得:
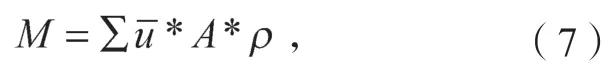
式中:M为自然通风量,kg/s;为流体的平均速度,m/s,且;A为太阳能烟囱通道横截面积,m2。
经计算整理后得到的模拟值与实测值在不同热流密度下的对比结果如图3所示。对比图3中的相关数据可知,模拟值与实测值对比误差在15%以内,误差可接受,验证了本模型可行。
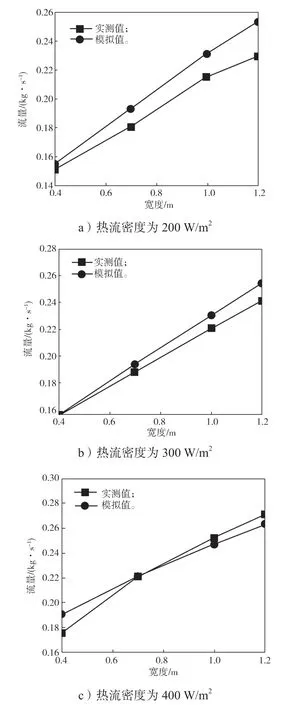
图3 不同热流密度下的模拟值与实测值结果对比Fig.3 Comparison of simulated and measured values under different heat flux
2 计算结果及分析
2.1 3 种自然通风方式下的风速对比
空气龄是指空气微团自流动开始到进入流场某一区域所需的时间,也可表示为外部洁净空气到达指定位置的时间。即空气龄越小,表示该区域的通风状况越好,反之通风效果越差。可用空气龄衡量室内空气的新鲜程度与换气能力。

本文在不同工况下分析厂房内气流流体流动、特殊位置空气速度,且以局部测点空气龄为评价指标,分析在风压与热压耦合下,太阳能烟囱高度一定时,针对其不同高宽比,对于自然通风的影响。
本文将工况分为3 种,当Hc一定时,在不同自然通风方式、不同高宽比情况下进行计算分析。首先,对太阳能烟囱高宽比为0.5,且存在内热源的情况下,对比研究3 种通风方式的空气状况,计算所得其整体通风速度云图见图4,空气龄云图见图5。
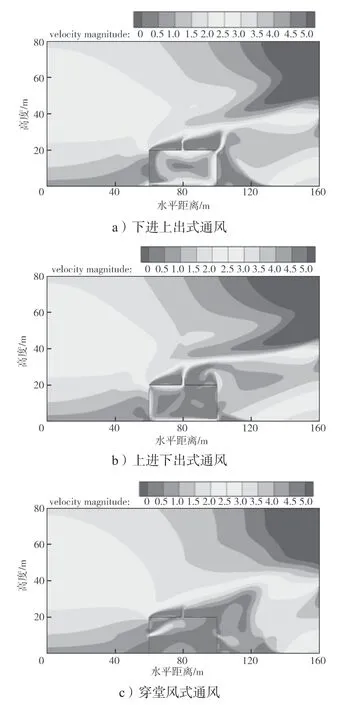
图4 3 种通风方式的整体风速云图Fig.4 Overall velocity cloud diagram of three ventilation modes
从图4所示风速云图可知,各建筑开口处的风速较大,以下进上出式自然通风开口处的风速阈值最大。各个通风方式下厂房内部均有低风速区域及涡流,但以下进上出式与穿堂风式低速区面积较小,下进上出式通风内部低速区主要存在于厂房中部与左部,穿堂风式通风方式的风低速区则存在于中部、左下与右侧,上进下出式低速区所占比例较高,仅在各个开口处与建筑壁面周围速度稍高。而对于太阳能烟囱处,3 种通风方式各有特点:下进上出式通风方式的太阳能烟囱的速度阈值较大,然而烟囱右部存在一个低速区,甚至是涡流;上进下出式通风方式下,平均速度较大,且低速区面积较小;穿堂风式通风方式下,平均速度较小,阈值较小,但在其烟囱下部气流速度较快。在各个通风方式下,厂房右侧开口处速度值虽大,但各有特点。下进上出式通风方式的阈值较高,面积较大;上进下出式通风方式的右侧出口流速略大于穿堂风式通风方式下的,但高流速面积小。气流速度大小仅可作为通风效果评价的参考数值,故引入空气龄评价指标继续对3 种通风方式进行计算与论证。
观察图5所示空气龄云图,无论哪种通风方式,其厂房中部存在气流停滞,但可明显看出,穿堂风与下进上出式通风方式,其空气龄数值高的部分都小于上进下出式通风方式的,且上进下出式通风大部分区域存在高空气龄,仅边缘处空气龄数值小。而下进上出式通风厂房内部的高空气龄区域较之穿堂风式面积小、数值低,但厂房右侧存在一个高空气龄区。通过比较3 种通风方式的空气龄与气流速度大小,可得出如下结论:选用下进上出式通风方式,自然通风效果最佳,但仍需在特殊位置处比较对应速度与空气龄,本文选择烟囱出口处、厂房右侧出口处,及H=2 m 处(设为工作区域高度)进行计算分析,速度值结果见图6,空气龄数值结果见图7。

图7 3 个特殊位置处的空气龄数值Fig.7 Air age values at 3 special positions
由图6可知,在烟囱出口处(图6a),上进下出式通风方式的整体风速皆大于穿堂风式通风方式的,然而下进上出式通风方式下,左部区域整体风速较高,阈值较大。右侧通风方式下,整体风速逐渐减弱,并逐渐低于另外两者,这可能是因其烟囱右侧的涡流所致。而在厂房右侧出口处(图6b),下进上出式通风方式的风速整体大于其他两种通风方式的,阈值较高,上进下出式通风方式的风速则仅有中部风速略高于穿堂风式通风方式的,且均值较低。针对H=2 m 的工作区域(图6c),下进上出式通风方式的风速整体仍比其余两种通风方式的风速高,且与穿堂风式通风方式的分布规律类似,呈中间高两边低的规律,但上进下出式通风方式的前部风速较高,中部风速虽有一定的增长趋势但并未超过另外两工况的,均值和阈值均较低。
如图7所示,烟囱出口处(图7a),穿堂风式通风方式的的空气龄基本上整体低于另外两种通风方式的,其仅在烟囱右部略高于下进上出式通风方式的。且三者空气龄均明显有左边低右边高的规律,通过以上云图可知,在下进上出式通风条件下,在其右侧还出现了涡流,证明了相应的规律。于厂房右侧出口处(图7b)而言,上进下出式通风方式具有更低的空气龄,且均值良好,而其在H=2 m 的工作区域(图7c)的空气龄值却不理想,其左侧较低,右侧较高,均值与穿堂风式通风方式的皆大于下进上出式通风方式的。
整体来说,由于厂房内部热源的存在,室内中部风速由于热浮升力皆有所加强,且将气流提升,所以下进上出式通风方式更适用于此类模型,其气流先由下部进入,经热源抬升后由上部出口流出,是较为理想的通风方式。将选用下进上出式通风方式进行探讨,在太阳能固定高度下,改变烟囱的宽度以达到不同高宽比,找出通风效果最佳的参考值。
2.2 不同高宽比的太阳能烟囱通风效果比较
本研究选取4 类工况(即高宽比分别为0.25,0.50,0.75,1.00)进行计算分析,通过计算分析相应风速与空气龄,以期找出最适合本模型的烟囱尺寸,计算所得不同高宽比太阳能烟囱速度云图见图8。
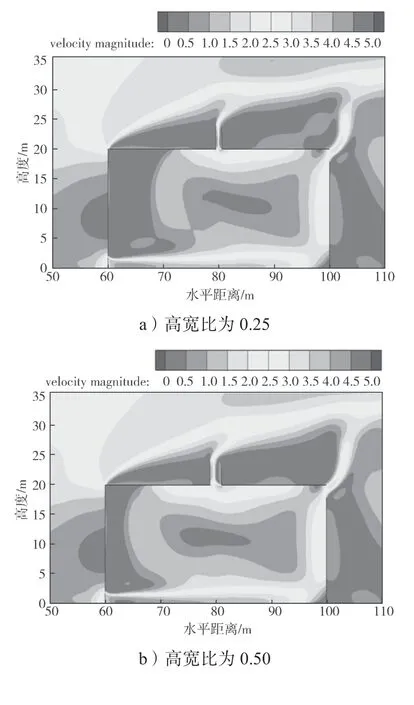

图8 不同高宽比下太阳能烟囱的速度云图Fig.8 Velocity cloud diagram of solar chimneys with different height-width ratios
由图8所示速度云图可知,在厂房内中部与左上部,均存在一个持续的低速区,不论是哪种高宽比,皆存在这个情况,但随着高宽比数值增大,其两低速区面积逐渐减小。在各不同太阳能烟囱高宽比速度云图中,烟囱右部无一例外出现了一个低速区,且烟囱的高宽比越大,低速区面积越大。在厂房下部存在一个高风速区,且均值较高,阈值较大。出现这一现象的原因可参考相应矢量图加以分析,因4 类工况呈现的规律存在统一性,故本文任选一工况进行分析,图9是太阳能烟囱高宽比为0.5 时的气流矢量图。

图9 太阳能烟囱高宽比为0.5 时的气流矢量图Fig.9 Airflow vector diagram with an aspect ratio of 0.5 of solar chimneys
由图9可看出,烟囱左侧存在的低速区是由于气流绕流与烟囱出口处气流相遇后滞留在此处导致的,而烟囱右侧的低速区仅是气流绕流导致的。由于厂房内下部风速较快,气流流动迅速,并遇到厂房右侧壁面后产生了向上与向左的气流组织,而后遇上由于底部热源产生“烟囱效应”所携带的气流,两者相遇在厂房中部及左侧产生了涡流。而烟囱内部右侧由于烟囱出口处气流与烟囱上部梯度风相遇,导致在右侧堆积低速区及涡流现象。本研究将通过空气龄比较各个工况的通风状况。计算所得不同高宽比下太阳能烟囱的空气龄云图见图10。
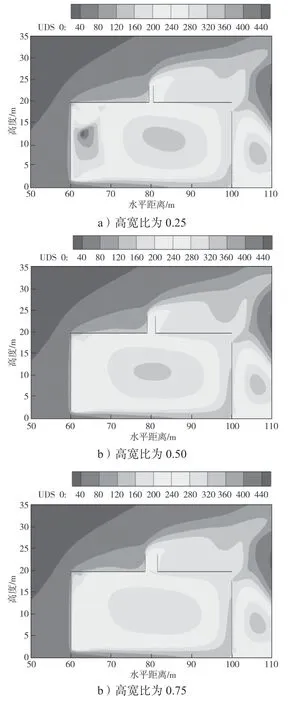
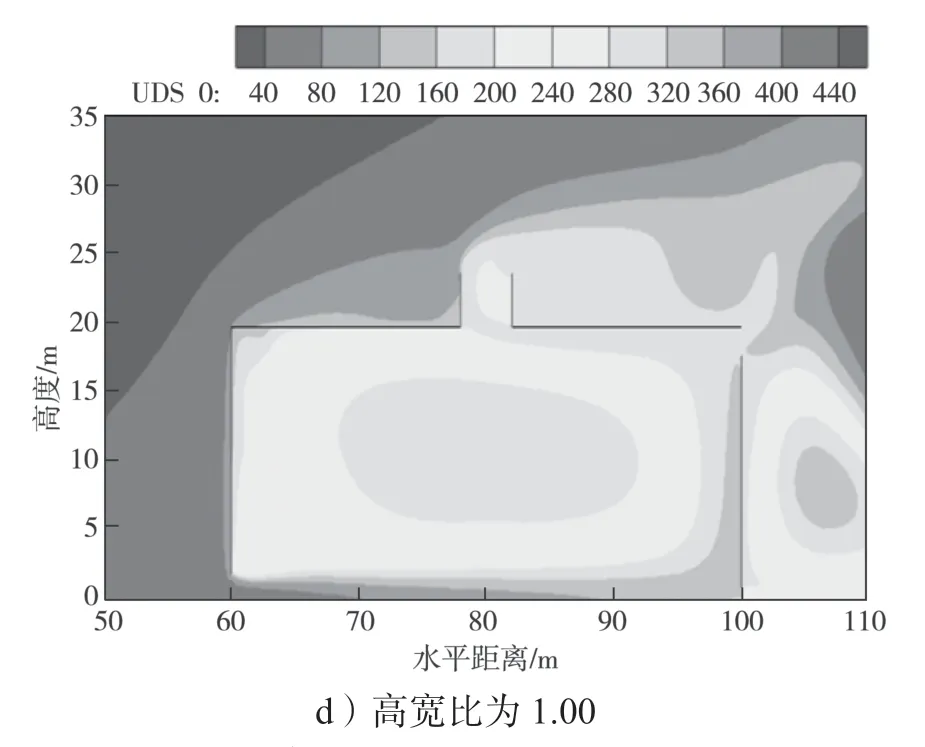
图10 不同高宽比下太阳能烟囱的空气龄云图Fig.10 Air age cloud images of solar chimneys with different height-width ratios
如上方描述,结合图10所示空气龄云图可知,厂房内部左侧的滞流随高宽比增大后有逐渐减小的现象。同时,太阳能烟囱内部及右侧出口处,空气龄与高宽比呈负相关,这是由于开口越宽,出流越大,与梯度风相遇后越易滞流。要选取最佳的高宽比,主要应该参考厂房内部空气龄,而由于厂房内部的特殊位置较多,应选取能囊括大部分特殊区域的空气龄提取位置。本文选择x=80,0 图11 厂房内中部区域的空气龄计算结果Fig.11 Calculation results of air age in the central area of the plant 由图11可知,在烟囱高宽比为1.00 时,其空气龄均低于另外3 种工况的,结合速度云图所得结论,确定本模型在下进上出式自然通风时,选取太阳能烟囱高宽比为1.00 左右拥有最佳的通风效果。 由上文论述,可得出以下结论: 1)通过3种自然通风方式的比较,以速度位参考、空气龄为评价指标,观察模型的总体云图,然后参考具体的特殊位置,两者并考,得知下进上出式自然通风方式的增益效果最为明显。 2)选取下进上出式自然通风方式,探讨太阳能烟囱不同高宽比对自然通风状况的影响,最终得知,以太阳能烟囱高宽比为1.00 时的通风效果最佳。 基于本文论述,提出如下改进建议: 1)针对单侧风向室内有热源驱动自然通风的情况,采用下进上出式通风方式,不失为一个优良的开口设置,但其室内气流中部区域存在低速区,可结合穿堂风式通风加以优化。 2)虽然太阳能烟囱高宽比越大,厂房内部整体空气龄愈弱,但是存在太阳能烟囱右部低速区面积愈大的情况。由于本文选定烟囱高度进行分析,存在一定的局限性。今后可选取不同高度,在不同高宽比情况下进行具体分析。 3)本文在太阳能烟囱高宽比变量范围选取上具有一定的局限性,应多加入不同范围进行计算。 4)本文仅对建筑内部风环境进行分析,由内部热源驱动,理查德森数远大于10,以自然对流为主导,对于强制对流稍弱的情况,可改变内部热源及太阳能烟囱壁面热流密度进行下一步的推导与求证。
3 结论与建议

