基于FLAC3D的深部隧道分区破裂特性研究

吴 政，梁 斌，祝方才，高乐星，邹长春

（湖南工业大学 土木工程学院，湖南 株洲 412007）

0 引言

随着科学技术的不断进步，在各种工程领域上的拓展逐渐深入，出现了许多不符合浅部围岩破坏方式的现象。在深部采矿工程中，进行深部地层开挖可能出现岩爆、分层破裂、分区破裂化等问题。与浅部工程相比，深部工程受到很大的地应力，使得变形及破坏与浅部工程有明显差异。分区破裂化现象是深部岩体破坏的一个典型特征[1]。

俄罗斯Taimyrskii 深层矿洞中出现的岩体交替破坏形式最早被定义为分区破裂化现象，相似现象陆续在其他国家被观测到。如E.I.Shenyakin 等[2]通过室内模型试验重现了分区破裂化现象，并在实际深部采矿工程中观察到了此现象的存在。分区破裂化问题在中国最早由钱七虎院士提出[3]，之后李术才[4]在学术沙龙中提出其使用钻孔电视在淮南矿区丁集煤矿岩层中发现分区破裂化现象；谭云亮等[5]在新汶矿区孙村煤矿深部巷道围岩中观察到分区破裂现象。分区破裂化现象逐渐被科研工作者们作为深部洞室、巷道围岩开挖破坏的特征和标志。

针对分区破裂化现象产生的原因，研究者们进行了多维度的尝试。就模型试验方面，袁亮等[6]利用总参工程兵科研三所研制的实验装置进行了深部围岩破裂试验，结果证实了洞室在较大轴向压应力持续作用下会形成交替的破裂区和非破裂区，即分层破裂现象。陈旭光等[7]通过模型试验，发现围岩应变呈现波浪形变化规律以及洞周锚杆受力出现拉压交替变化现象。张智慧等[8]利用相似材料制作了多种不同模型，对分区破裂时裂纹的分布和沿巷道轴向的变化规律进行研究。

在理论分析方面，王明洋等[9]围绕围岩力学、变形两方面进行探究，得出结论为围岩最大压力区的体积是影响分区破裂化现象产生的因素之一，并且以此条件为基础，划定了深、浅部工程活动的界限。周小平等[10]把开挖过程看成动力问题，分析了分区破裂与巷道开挖的速度、岩石强度的关系。Wu H.等[11]将塑性区发育过程中岩体的蠕变破坏视为分区破裂化的一个因素。V.N.Odintsev 等[12]在研究分区破裂化问题时简化了隧道开挖的三维问题，提出的初始破坏准则用于平面应变问题。其他研究者[13-19]在数值模拟方面进行了大量研究。王红英[20]、李树忱[21]、高富强[22]、唐礼忠[23]在数值模拟研究方面得出了一些结论，但对深部岩体本身力学性质没有展开全面分析。深部地层特有的高地应力环境是影响巷道围岩稳定性、大变形、岩爆等问题的重要因素，为了保证地下工程的正常施工，防止工程事故发生，完善深部工程理论，高地应力作用下的硐室围岩变形及支护对策亟需展开相关研究。因此，在本研究中，以应力应变软化本构模型为基础，对某煤矿深部开挖出现的分区破裂化现象进行模拟分析。探讨原岩应力、内摩擦角两个参数对深部岩体分区破裂的影响，以期为相关研究及工程提供补充和参考。

1 模拟原型与研究方法

1.1 模拟原型

本文的模拟原型为淮南矿区某采区巷道，围岩以破碎带形式出现的带状崩解并不是完全连续的。深部巷道中实测发现的分区破裂化即为围岩内部破裂区和完整区，为交替出现的现象，如图1所示。

图1 煤矿围岩分区破裂实测现象和传统破裂示意图Fig.1 Schematic diagram of zoning fracture of surrounding rock in the coal mine and schematic diagram of traditional fracture

1.2 研究方法

对于地质环境复杂的工程，模型试验通常无法对其进行还原，常采用数值方法进行模拟。其中，有限元法因为考虑了岩体的非连续性、适用于处理复杂边界问题成为岩土工程分析最常用的方法之一。

在有限元方法基础之上开发有限差分软件FLAC3D能更好地考虑岩土体的不连续性和大变形特征，考虑岩体破裂而非分离来研究带状破裂问题，因此，本研究选择FLAC3D作为连续介质数值分析的数值模拟软件。

2 应变软化本构模型的构建

应变软化模型以摩尔库仑模型为基础，其弹性阶段与摩尔库仑模型一致，区别在于摩尔库仑模型中各个参数在模拟计算过程中都是恒定不变的，而在应力软化模型中，强度参数都会随着塑性应变变化。并且可以通过FLAC3D自带的Fish 语言根据需要模拟的内容自定义岩体强度参数与塑性应变函数。应变软化模型的应力-应变曲线如图2所示。

图2 应变软化模型应力-应变关系曲线Fig.2 Strain softening model stress-strain relationship

强度低于屈服强度时，总应变为弹性应变，即

当强度到达屈服强度以后，总应变包括弹性应变与塑性应变，即

其中，塑性应变又包括塑性剪切应变与塑性拉伸应变，表达式为

将式（3）代入式（2），可变为

2.1 弹性法则

主应力与主应变形式的胡克定律表达式为

式中：α1=K+(4/3)G，α2=K-(4/3)G，其中K为体积模量，G为剪切模量。σ1、σ2、σ3分别为第一、第二、第三主应力。

2.2 屈服函数与势函数

FLAC3D中，应变软化模型剪切屈服函数为

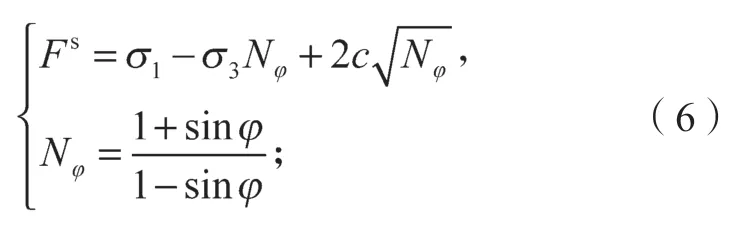
式中：φ为内摩擦角；c为黏聚力。

拉伸屈服函数为

剪切势函数为

拉伸势函数为

2.3 剪切破坏应力修正

剪切破坏时，根据正交流动法则，有

根据拉伸破坏流动法则，有

式中λ为特定的塑性系数。

将式（10）展开，得：

式中ψ为剪胀角。

将式（12）代入增量弹性法则式（5），可得剪切破坏应力修正为

3 数值模型的构建

建立淮南矿区某巷道模型，其网格划分立体图如图3所示，模拟长度为50 m，隧道半径为5 m。该计算模型被离散成55 000 个单元。

图3 巷道模型网格划分立体图Fig.3 Meshing diagram of tunnel model

岩石的物理力学参数见表1，为还原实际工程状况，数值模拟时模型底部固定，初始位移和速度为0。

表1 岩石的物理力学参数Tab1e 1 Physical and mechanical parameters of the rock

在计算时采用两种本构模型，第一种为摩尔库仑模型，第二种为应力应变软化模型。在摩尔库仑模型中，对比岩体的两种强度即峰值强度和残余强度。计算结果如图4和5 所示。

图4 基于摩尔库伦本构模型的模拟计算结果Fig.4 Simulation results based on Mohr Coulomb constitutive model

从图4所示计算结果可以发现，自巷道开挖后，出现了一条明显的环状塑性带状区域，即分区破裂化现象。图4a 模拟的破坏方式与浅部巷道破坏方式一致，图4b 的围岩内部出现部分塑性破坏。

在FLAC3D的应力应变软化本构模型中，岩体的弱化与塑性应变有关，当岩体逐渐发生塑性应变时，岩体的抗剪强度、黏聚力、内摩擦角逐渐降低，以此实现岩体软化过程。当塑性剪切应变达到极限值时，岩体被破坏，计算结果如图5所示。

图5 基于应力应变软化本构模型的模拟结果图Fig.5 Simulation results based on the stress-strain softening constitutive model

对比图4和5，可得知应力应变软化本构模型比摩尔库仑模型更适用于模拟深部岩体的应力应变特性。

4 影响因素分析

4.1 原岩应力对分区破裂现象的影响

以上述模型为基础，计算出围岩的单轴抗压强度为17.32 MPa。取原岩应力变化区间为10～35 MPa，控制变量，改变原岩应力参数，研究原岩应力增长对分区破裂现象产生的影响。结果见图6a～e，图7为不同原岩应力对分区破裂化体积的影响。

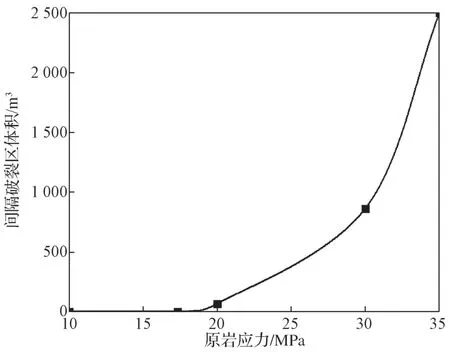
图7 原岩应力对间隔破裂区体积的影响曲线Fig.7 Effect curve of the original rock stress on the interval fracture zone volume

由图6和7 可知，当原岩应力小于17.3 MPa（即单轴抗压强度）时，巷道破坏方式同浅部隧道破坏方式一致。增大原岩应力到20 MPa，围岩内部分区域产生塑性变形无成环状趋势，V=0.755 2×102m3。继续增大原岩应力，塑性区范围增大，直到原岩应力增至30 MPa，出现了明显的封闭环状塑性区，此时V=8.626×102m3。原岩应力增大至35 MPa 时，V=25.00×102m3。可得出深部围岩出现分区破裂化现象的重要前提为原岩应力大于岩体的单轴抗压强度。塑性破坏区域的数量与原岩应力的大小呈正相关关系。

图6 不同原岩应力条件下的分区破裂数值计算结果图Fig.6 Zonal fracture numerical calculation diagram under various original rock stress conditions

4.2 强度参数对分区破裂现象的影响

本研究讨论不同强度参数摩擦角φ对分区破裂现象的差异，推理其影响关系。此处参考文献[1]，根据深部围岩内摩擦角实际变化范围，随机取值22,26,30,34,38 °进行模拟计算，结果见图8，塑性区体积变化如图9。

图9 内摩擦角对间隔破裂区体积的影响曲线Fig.9 Effect curve of the internal friction angle on the volume of interval fracture zone

根据图8和9 可知，随着摩擦角φ的逐渐增大，岩体的塑性范围逐渐减小；当φ=22°时，塑性区体积V=26.867×102m3，且在破裂带外围有形成第二条破裂带的趋势；当φ=26°时，V=17.995×102m3；当φ=30°时，V=13.849×102m3；当φ≥38°时，围岩出现与传统破坏模式相同的现象。可能的原因是内摩擦角与岩体抗压强度呈正相关，在原岩应力一致的情况下，当φ=22°时，岩体单轴抗压强度小于原岩应力且差距较大；内摩擦角增大到26,30 °时，原岩应力仍大于岩体单轴抗压强度，但差距缩小，此时岩体塑性区依旧有分区破裂化现象；当内摩擦角增大到34°时，V=0 m3，围岩无明显分区破裂化现象，此时岩体单轴抗压强度大于原岩应力。

图8 不同φ 值下分区破裂数值计算结果图Fig.8 Numerical calculation result diagram of partition rupture under different φ value conditions

5 结论

1）深部岩体破坏方式与浅部迥异，在进行深部岩体数值模拟研究中，应力应变软化本构模型具有良好的适用性，深部巷道出现分区破裂化现象的一个重要前提为原岩应力大于岩体单轴抗压强度。

2）深部岩体分区破裂化现象受原岩应力影响显著，随着原岩应力的增大，分区破裂带逐渐深入，且当原岩应力小于35 MPa 时深入速度呈上升趋势。

3）φ的变化对分区破裂现象影响显著。内摩擦角与岩体抗压强度正相关，当φ=22°时塑性区体积最大。随着内摩擦角增大，岩体单轴抗压强度增大，塑性区体积减少。当φ≥38°时，围岩出现与传统破坏模式相同的现象。