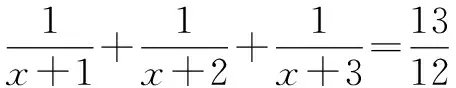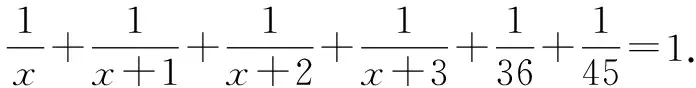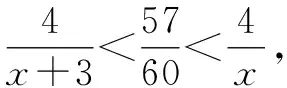初中数学解题中放缩法的运用分析
⦿江苏省南京市第八中学 李鸣午
在最近的初中数学竞赛题乃至教材(比如苏科版等)中都陆陆续续出现了借助于放缩法理论工具进行解答的试题.可见,放缩法在初中数学解题中的重要性愈来愈明显.笔者结合具体的例子尝试着对放缩法在初中数学中的具体运用展开分析,归纳提炼出解题的方法及思考路径.通常而言,把代数式子的某个具体项或是某一项所涉及到的某个具体因式加以放大或是缩小处理即不等取代,从而使它向结论的方向转化的一种数学方法,叫“放缩法”.比如,在证明A 放缩法在初中数学不等式习题中是常用的一种方法.借助于放缩法的特性,可以巧妙地化解有关不等式的证明问题[1]. 综上所述,原不等式成立. 初中数学问题中,有一类习题是关于最值的问题.一般情况下,当难以顺利地确定出最大值或者最小值时,合理运用放缩法,便可以有效化解这一类最值问题. 例2已知二次函数y=x2+ax+b的图象和x轴2个交点对应的横坐标依次是m,n,同时|m|+ |n|≤1.假定与上述的条件相吻合的b对应的最大、最小值依次是P,Q,试求|P|+ |Q|的数值[2]. 解:由m,n为一元二次方程x2+ax+b=0的2个实根,根据韦达定理,可知m+n=-a,mn=b. 又|m+n|≤|m|+|n|≤1,|m-n|≤|m|+|n|≤1. 由于原方程式存在实数根,因此Δ≥0,也就是a2-4b≥0. 初中数学习题中,经常遇到有关完全平方数的问题.由于完全平方数本身具有性质上的独特性,如果能够有意识地把握住这一点,同时合理运用好放缩法这一工具,能够使这类问题迎刃而解[3]. 例3求使m2+m+7属于完全平方数的全部整数m的值. 解析:(1)如果m≥7,那么m+7≤2m. 因此,m2+m+7处于2个连续的整数的平方之间,而非完全平方数. (2)如果0 (3)如果m=0,那么m2+m+7的值为7,非完全平方数. (4)如果m<0,那么使n=-m,由于n为正整数,因此m2+m+7=n2-n+7.就二次三项式n2-n+7而言,如果n>7,那么-n<-7,且有-n+7<0.也就是n2-n+7 如果n≤7,将n=1,2,3,4,5,6,7依次代入到n2-n+7中,通过运算可以发现,仅仅在n=2或7的时候,n2-n+7属于完全平方数.因为n=-m,所以m=-2或-7. 综上所述,与条件相吻合的整数m的值分别为1,6,-2,-7. 上述问题的化解,不仅仅使同学们掌握了借助于放缩法判断单个整数是否属于完全平方数的手段,同时训练了数学思想方法中重要的分类讨论法.对上述问题还能够进行以下的变式练习:当n为自然数时,求证4n2+4n+4不可能属于完全平方数. 初中数学习题中,不定方程问题相对比较复杂,如果按部就班地求解,步骤显然会变得非常繁琐.此时,恰当地使用放缩法可以达到事半功倍的效果[4]. 综上所述,方程的正整数解是x=1. 事实上,上述有关不定方程的相关问题能够进一步推广到以下例子. 由x>0,可得 由于x为正整数,因此x=2,3,4. 通过检验x=3符合题意. 故a=3,b=4,c=5,d=6. 综上所述,基于以上4个不同的初中数学题型的探讨及其解答,不难发现放缩法在初中数学解题教学中具有非常重要的作用.按照中学数学课程标准中“要培养学生分析问题和解决问题的能力”的相关要求,在初中数学教学中,应有意识地培养数学思想方法的有效运用,并达到创新性使用的目的.因此,通过放缩法的运用,有意识地培养学生的“应用数学意识”,并落实到初中数学解题的教学中去,使学生了解数学的广泛应用,从而提高学生对数学学习的兴趣,并逐步形成运用数学知识解决问题的良好习惯.1 不等式问题中放缩法的运用
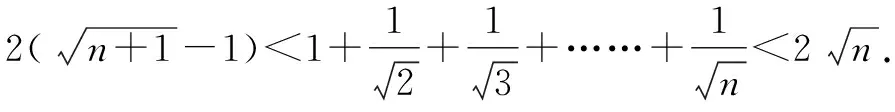


2 最值问题中放缩法的运用


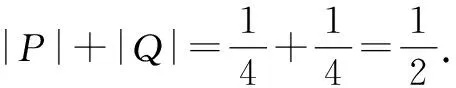
3 完全平方数问题中放缩法的运用
4 不定方程问题中放缩法的运用