巧借数学活动经验 提升数学教学品质

⦿苏州工业园区星澄学校 吕 琴

随着新课改的不断推进，课堂目标由“双基”变成了“四基”，增加了基本经验和基本思想，可见数学经验越来越受到教育者的重视.笔者从具体教学实践出发，谈了几点数学活动经验在理解知识、内化知识、优化认知等方面的应用，以期能够让教师在实际教学中重视学生数学活动经验的积累，并将活动经验转化为推动学生学习能力提升的内驱力，从而打造高品质数学课堂.

1 巧借直接数学活动经验，理解知识

直接数学活动经验主要来源于生活，是直接联系日常生活经验所获得的数学活动经验.面对抽象的数学问题时，学生有时难以进入“角色”，此时，若将生活经验融入到课堂教学活动中，有助于帮助学生突破难点，让学生更好地理解数学.

案例1三角形的高

对于三角形的高这一知识点学生并不陌生，在小学就学习过，不过到了初中，部分学生在作钝角三角形的高时，仍然感觉有些困难.为了解决这个问题，教师在教学中设计了这样两个问题：

问题1高楼大厦的高怎么画？

问题2倾斜的宝塔高怎么找？

问题给出后，学生脑海中自然浮现出这些场景，凭借直接经验轻松地回答问题.可见，利用直接的活动经验既可以让学生更好地理解数学，也可以引导学生用数学的眼光看待生活，从而将数学与生活紧密地联系在一起，帮助学生领会数学的本质[1].

2 巧借间接数学活动经验，辨析本质

所谓间接数学活动经验指的是学生通过书本、教师讲授等其他途径获得的一些知识和经验.在教学中，教师要根据具体的教学内容组织适当的数学活动，如借助具体情境引导学生构建数学模型，引导学生运用数学知识解决实际问题，让学生更好地认识数学本质.

案例2有理数的乘法

师：在小学阶段我们就学习了乘法，对于3×2如何用加法来表示呢？

生1：3个2相加，即2+2+2；或2个3相加，即3+3.

师：很好，接下来我们用一个具体的事例来说明.现有一只小虫以3 dm/min的速度自西向东沿直线爬行，那么2 min后，小虫位于原来的什么位置？

生齐声答：向东6 dm.

师：很好！规定由西向东爬行的方向为正，你能将上面问题用数轴表示出来吗？(问题给出后，学生积极操作，画出了图1.)

图1

师：反过来，若小虫以3 dm/min的速度由西向东沿直线爬行，2 min后，小虫位于原来的什么位置？

生齐声答：向西6 dm.

师：如果在数轴上表示，该如何表示呢？(学生给出了图2.)

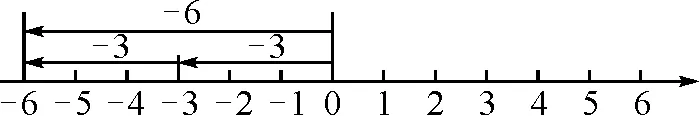
图2

师：你能用乘法表示出来吗？

生2：(-3)×2=-6.

师：你能借助生活经验解释(-3)×2=-6的实际意义吗？

生2：每道选择题3分，做错两题共扣了6分，记作-6.

生3：登山队攀登一座山峰，每攀登1 km气温下降3 ℃，攀登2 km后，气温有什么变化呢？

…………

这样将生活与数学完美地融合在一起，引导学生借助间接经验建立模型，帮助学生理解有理数的乘法.同时，将数学知识融于实际生活中，淡化了数学的抽象感，让学生获得了广泛的数学理解，有助于学习能力的提升.

3 巧借意境联结数学活动经验，内化知识

数学概念、定理、结论等内容大多是在生产生活和数学实践中逐渐抽象而来的，具有与生俱来的抽象感，为了淡化其抽象感，在教学中不妨将其还原至具体情境，引导学生通过联想、类比、举例等方法，体验其本质及其中蕴含的数学思想方法，以此帮助学生理解、内化知识[2].不过，这类活动经验并不是直接产生于实际活动中，而是通过比喻、联想等活动有意架构的，从而帮助学生找到一个易于理解、易于接受、易于实现的落脚点，让抽象的内容生动化、具体化，以此建构生动的、高效的数学课堂.

案例3有理数的乘法

在教学有理数的乘法法则时，大多数教师会直接给出运算法则，或者给出一些具体实例让学生通过模仿、联想等学习活动进行抽象，从而让学生通过记忆、模仿等活动理解并掌握知识.从应用的角度来讲，这种教学过程是高效的，学生可以直接应用法则解决问题，但从激发学生学习兴趣的角度来分析，以上教学过程略显枯燥.其实，教师在教学中不妨创设一些生活情境，带领学生体验抽象内容的形成、发展和应用过程，以此激发学生的数学学习兴趣.

师：刚刚我们学习了有理数的乘法，知晓了它的运算规则，其实这个运算规则可以用生活实例来表达.现在通过“我问你答”的方式考考大家，看看这些生活实例和哪个法则相对应？

师：朋友的朋友是朋友.

生1：正正得正.(生1抢答)

师：很好.朋友的敌人是？

生2：敌人，正负得负.

师：很好，按照这个规律说下去，你还能得到什么？

生3：敌人的朋友是敌人，这个说的是“负正得负”.

生4：敌人的敌人是朋友，这个就是“负负得正”.

师：真棒！你还能想到其他生活实例吗？

有了前面的铺垫，学生积极联想，又列举了一些其他事例，如将好人、坏人，好报、坏报与好事、坏事建立联系，进一步体验规则.

这样将抽象的内容与实际情境建立联系，不仅实现了知识的内化，而且彰显了数学文化的教育价值.数学教学中，在关注教学结果的同时，也要重视教学过程，善于借助已有的认知基础等经验，让学生更好地理解数学的本质，提升教学的有效性[3].

4 巧借专门设计的活动经验，优化认知

专门设计的活动经验是为具体的数学学习内容服务的，其更加具体、形象，更具操作性，也更有数学味.在教学中，教师可引导学生通过“动手做”体验数学，获得成功经验；通过“动脑想”逐渐形成概念、结论、定理，以此让学生在具体操作中获得数学活动经验，优化认知.

案例4求证：三角形的三个内角和等于180°.

分析：本题在证明时需要添加辅助线，但是对于刚刚接触几何证明的学生来讲，这个过程无疑是复杂的，难以理解的.为了降低问题的难度，让学生获得直观感受，大多数教师会通过折叠、拼贴等具体实验来启发学生，让学生自主地完成辅助线的添加.

在具体实施过程中，大多教师会抛出这样的问题：之前我们是怎样发现三角形的内角和是180°的呢？有的学生想到了拼贴法，有的学生想到了折叠法，有的学生想到了测量法，课堂气氛活跃.不过在此基础上引导学生添加辅助线时，学生仍然一筹莫展.可见，通过以上具体操作并没有让学生有更多收获.究其原因是以上教学过程缺乏针对性的引导，学生一直在原有的实验环节中徘徊，并未取得新的突破.基于此，教师做了如下引导.

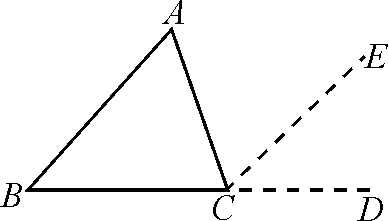
图3

师：如图3，将∠A剪下来拼到∠ACE的位置，将∠B将下来拼到∠DCE的位置，于是有∠A=∠ACE，∠B=∠DCE.若不用“剪、拼”的方式，是否能够得到∠ACE呢？(生沉思)

生1：由∠A=∠ACE，我想到了两条平行线的内错角，过点C作CE∥AB，即可得到∠ACE.

师：很好！这样是否可以证明了呢？

在教师的引导下，学生借助已有的实验经验，通过角相等想到了平行线，继而通过添加辅助线顺利地完成了证明.

师：还有其他添加辅助线的方法吗？

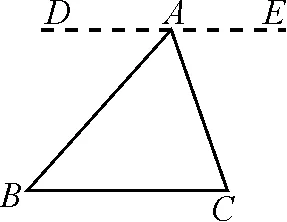
图4

生2：如图4，将∠C剪下来拼到∠EAC的位置，∠B剪下来拼到∠DAB的位置，于是有∠EAC=∠C，∠DAB=∠B，它们都是一对内错角，所以我想到过点A作DE∥CB.

这样添加辅助线的思路打开后，证明的方法也就应运而生.学生又尝试应用其他方式添加辅助线，如在BC上任取一点D，过点D分别作DE∥AB，DF∥AC，通过构造同位角进行证明，等等.

这类活动经验是无法从生活实际中直接获取的，需要在学习数学和应用数学的过程中不断积累.这类活动经验直接影响着学生思维能力和解题能力的提升，因此在实际教学中，教师要有意识地引导学生进行总结归纳，使其转化为数学知识的有机组成部分.

这些数学活动经验都是在日常生活、学习和实践中获得的，其既与知识有着相同的一面，也具有特殊性，更侧重于亲身经历和体验.因此，在实际教学中，教师要带领学生经历知识的形成和发展过程，有意识地帮助学生积累数学活动经验，从而帮助学生更好地认识数学、理解数学、应用数学.

总之，在数学教学中，教师要善于借助各种数学活动帮助学生积累数学活动经验，从而在经验的驱动下让学生学会发现、学会探究、学会应用，成就高效数学课堂.