挖掘教材,培养学生的“读思达”能力*
⦿福建省诏安县教师进修学校 胡惠颜 黄爱平
数学教材是教材编研人员根据国家对基础教育的定位、当代科技进步与社会发展状况的要求,同时结合学科的特点、社会文化、艺术、生活的需求、学生的年龄特点等编写出来的.教材中的内容、例题、习题都是经过了教材编研人员的精心选择编制,是教材编研人员集体智慧的结晶,它的作用主要是为教学活动提供一个必要的准则和依据[1].教师作为教学活动的执行者,必须根据课程标准要求和学生的认知水平,充分把握教材编委们留下的“教材运用创造空间”,挖掘、整合运用教材的显隐性课程资源,形成新的课程学习资源,明白要教什么、怎么教、教到什么程度,学生学什么、怎么学、学习目标是什么[2],才能合理高效地运用教材.因此,在“双减”背景下为了切实提高课堂教学效率,充分挖掘并运用教材,培养学生的“读思达”能力,显得尤为重要.
何谓“读思达”能力?读就是阅读.数学的阅读不同于语文、英语学科的阅读,不仅要读懂教材文本中的定义、定理、法则、性质、例题、习题等阅读材料,还要懂得在阅读的过程中把文字语言、符号语言和图形语言进行相互转换.“思”就是运用数学思想方法进行分析思考、探究理解、感悟.通过课堂教学揭示数学定义、定理、法则、性质的形成和发展过程,引导学生理解、认识数学的本质,掌握数学知识,感悟数学美,获得数学学习的愉悦感.“达”就是数学语言表述、规范的书面解答.数学语言是指对数学概念、算式、公式、运算、运算定律、法则及解题思路、推理过程等的表述,有文字语言、符号语言、图形语言,具有严密、准确、简练、抽象、符号化及严谨的逻辑推理等特点.苏联数学教育家斯托利亚尔说过:“数学教学也就是数学语言的教学.”因此,在日常的课堂教学中,培养学生规范的数学语言表述就要从培养学生的“达”开始.
下面,笔者以北师大版初中数学教材为例,漫谈如何挖掘并利用教材的显隐性课程资源,培养学生的“读思达”能力.
1 科学设计课堂教学环节
在课堂教学中,培养学生“读思达”能力的各个环节应当是相互交错、互相渗透、相辅相成的.以北师大版数学九年级下册第三章第五节“直线和圆的位置关系”为例,浅析课堂教学“读思达”能力的培养.
案例1“直线和圆的位置关系”新授课教学片段
第一个环节:引读导达引思.
引读:让学生阅读书本第89页的内容.
导达:让学生动手在纸上画一个圆,把直尺的一边看作直线,移动直尺,根据直尺移动时与圆的各种位置情况,画出图形.
引思:直线和圆有几种位置关系?有几个公共点?最多几个点?最少几个点?
导达:
(1)师生共同归纳总结出直线和圆的三种位置关系,并让学生理解掌握切线的定义.
(2)下列各题是否正确?请说明理由.
①直线和圆最少有两个公共点;( )
②如果直线与圆相切,那么直线和圆只有一个公共点;( )
③如果A,B是⊙O外的两点,那么直线AB与⊙O相交.( )
引思:由练习题的解答进一步理解“直线和圆的位置关系”,并引导学生思考能否类比“点和圆的位置关系”进行数量分析.
引读:让学生阅读书本第66页的“想一想”这部分内容.
引思:类比“点和圆的位置关系”,如果⊙O的半径为r,圆心O到直线l的距离为d,那么直线和圆的位置关系如何用r与d的大小关系来表达?反之,如何根据r与d的大小关系来确定直线和圆的位置关系?
导达:由上面的思考和类比,利用数形结合思想,鼓励学生用r与d的数量关系,归纳总结出直线与圆的位置关系的性质和判定.
引读:让学生阅读并完成书本第89~90页的“想一想”.
引达:让学生完成下面填空题.
①已知⊙O的半径为5 cm,圆心O到直线a的距离为3 cm,则⊙O与直线a的位置关系是______,直线a与⊙O的公共点有______个.
②已知⊙O的半径为4 cm,圆心O到直线a的距离为4 cm,则直线a与⊙O的位置关系是______,直线a与⊙O有______个公共点.
③若⊙O的半径为r,且圆心O到直线a的距离为5,则r的取值范围是______时,⊙O与直线a相交.
④直径为a的一枚硬币沿着直线滚动一圈,圆心的运动轨迹长为______.
第二个环节:由思、达引读.
通过第一个环节的教学,学生理解并掌握直线与圆的三种位置关系,理解“圆心到直线的距离与半径之间的数量关系”和“直线与圆的三种位置关系”的对应与等价关系.在此基础上,让学生阅读书本第89页的三幅图(图1),教师利用多媒体动画播放:太阳从海平面冉冉升起,上升过程中与海平面呈现的位置关系.

图1
在此基础上,教师还可以引导学生朗读唐朝王维的《使至塞上》:“单车欲问边,属国过居延.征蓬出汉塞,归雁入胡天.大漠孤烟直,长河落日圆.萧关逢候骑,都护在燕然.”让学生在朗读中,欣赏“大漠孤烟直,长河落日圆”的美丽景象,体会图1所蕴涵的数学意境——直线与圆的位置关系,在欣赏美景诗词中感悟数学美,培养学生用数学的眼光观察世界[1].
2 运用教材的“问题解决”内容
北师大版教材的编排特点是螺旋式上升,由浅入深,从易到难,配有大量的议一议、做一做、想一想、数学理解、问题解决、联系拓广等[3].教师作为使用这套教材的执行者,应当充分挖掘并运用教材的这些资源培养学生的“读思达”能力.
案例2八年级上册第174页的“问题解决”
北师大版八年级数学上册最后一章“平行线的证明”第三节“平行线的判定”,是初中阶段数学演绎推理、规范表达的示范课.这节课学生才真正接触到文字命题题型的证明,是一节几何演绎推理的入门课.演绎推理对于学生来说是一个崭新的学习内容,学生会感到困难甚至无所适从.因此,在入门教学时对学生的学习方法进行指导,引导他们进行“读思达”显得尤为重要.案例2是这节课课后习题7.4的最后一道题目,是一道几何文字题.引导学生对这道题目进行“读思达”,能有效地巩固“平行线的判定”这节课的演绎推理和数学语言的规范表达.
第一环节:引读、激思、导达.
引读:①首先引导学生读题,对题目的关键字、词、句要标识、标注,加深理解、提炼.本题的关键字和词有直角尺、画、直线a和b、两条平行线.②引导学生学会把题目分成题目的情景、所给的条件 、需要说明的问题这三部分.每一部分都要仔细读,有条件的还要反复读,才能把握题目的实质.本题的题目情境是木工师傅画平行线;所给的条件是木工师傅用的工具是直角尺,也就是画出来的两条线都是垂直于同一条直线;需要说明的问题是这两条直线平行.
激思:教师和学生一起分析思考本题的已知条件(已知部分)是什么,结论(求证部分)是什么,再引导学生画出符合题意的图形,然后根据图形,将题目的文字语言转化为符号语言.
导达:在引读激思后,让学生先用数学语言表达出本题,教师纠错,然后师生共同用严谨的逻辑推理和数学语言把本题表述出来.
已知:直线a⊥直线l,直线b⊥直线l(如图2).求证:直线a∥直线b.
证明:如图2,
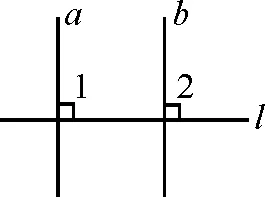
图2
∵ 直线a⊥直线l(已知),
∴∠1=90°(垂线的定义).
∵ 直线b⊥直线l(已知),
∴∠2=90°(垂线的定义).
∴∠1+∠2=180°(等式的性质).
∴直线a∥直线b(同旁内角互补,两直线平行).
第二个环节:由达再引读抛思.
引读:在第一环节的“导达”之后,要求学生重新多读本题几遍,让学生明白实际生活中处处有数学问题,要用我们所学到的知识来思考、表达、理解这些数学问题[1].
3 挖掘教材“脉络”
深度研读北师大版教材的编排特点,还可以发现:不同知识点的编排运用“交替式增长”模式,知识内容区间是有“脉络”的,有前后的关联也有纵横交错的联系[3].所以,培养学生的“读、思、达”能力,就不能只着眼于本节课或本单元知识的“读、思、达”,要从整套教材出发,把握知识点间的联系,引领学生从“点”到“面”到“多维”的“读、思、达”,引导学生反复“读”,反复“思”,抓住知识间的联系,实现对知识的重组和深度建构,从而培养学生的“读思达”能力.
案例3“二次函数”复习课的教学片段
学生在学完“二次函数”这章后,基本上已经掌握了二次函数的概念、图象及性质,所以,在复习课上可以通过设置一些相关的问题,引领学生“读思达”.
第一环节:引达抛思引读.
引达抛思:(1)什么是二次整式?写出几个关于x的二次整式.
(2)令你所写的关于x的二次整式为0,想想这是我们学过的什么内容?
(3)令y等于你所写的关于x的二次整式,想想这又是我们学过的什么内容?
引读:在学生回答完这三个问题后,教师引导学生再次回读教材——①七年级上册第87至88页有关整式的内容;②九年级上册第31至32页有关一元二次方程的内容;③九年级下册第29至30页有关二次函数的内容和第51至52页有关二次函数与一元二次方程的内容.
第二环节:引思引达再引思.
在学生读完相关教材内容后,引导学生通过观察对比思考:整式、一元二次方程、二次函数是有关联的,有什么关联?它们之间又有什么内在联系?通过对这两个问题的回答促进了学生对二次函数“面”的建构.
第三个环节:引达抛思.
在复习完二次函数图象与性质后,提出:(4)令你所写关于x的二次整式大于或小于0,你们又有什么发现?学生通过对这个问题的理解和表达,可以感悟到整式、一元二次方程、二次函数和一元二次不等式之间的关系.然后提出:(5)虽然我们还没有学习二次不等式的解法,但能否借助二次函数的图象与性质来解决这个问题?先由学生思考,教师再引导学生根据二次函数的图象及性质简要地解答这个问题,实现了二次函数从“点”到“面”到“多维”的拓展,进一步提升了学生的“读思达”能力.
爱因斯坦曾经说过:知识是会忘记的,留下来的是教育.掌握知识不是教育的最终目的,培养获得知识的能力才是教育的最大目标[2].所以,在“双减”背景下,教师应当充分挖掘并运用教材资源,培养学生的“读思达”能力,促进学生核心素养的形成和发展.

