隧道磁阻加速度计温度补偿技术研究*
周 煜,李育成,徐大诚
(苏州大学微纳传感技术研究中心,江苏 苏州 215006)
随着微机电系统(micro-electro-mechanical system,MEMS)的高速发展,隧道磁阻(Tunnel Magneto-Resistance,TMR)传感器凭借其高灵敏、低功耗、小型化的特性在惯性测量领域得到了广泛应用[1]。通过力、磁、电多物理场耦合实现加速度高精度测量已经成为可能。2008年埃因霍温理工大学[2]利用磁阻传感器检测质量块偏转导致的磁场变化量来实现加速度信号的检测。2017年,Crocus Technology公司[3]提出了一种基于磁性逻辑单元(Magnetic Logic Unit,MLU)的双轴加速度计。近年磁阻加速度计在国内也开始引起重视[4],2019年中北大学[5]基于TMR效应设计了一款三轴加速度计装置;2020年,东南大学[6]将平面主结构与隧道磁阻传感器进行微组装,制成z轴方向的隧道磁阻加速度计样机,最终可实现1.7 mV/gn的灵敏度,128 μgn/的分辨率。这些报道主要在测量系统组成方面,而有关温度性能的研究目前报道较少。目前针对该类器件的温度补偿主要有两大类,一是硬件补偿,一般是根据输出函数与温度的传递函数,来选择不同的电路拓扑结构,最终通过计算匹配进行补偿或者利用恒流源补偿、恒压源补偿、PN负温度系数补偿等方法补偿[7-8],虽然硬件电路补偿简单,但是其灵活性和精度有限;另一种是软件补偿,软件补偿有精度高、移植性强的特点。它是通过温度实验建立模型来对加速度计进行补偿,常用的建立温度模型的方法有分段线性差值、多元回归分析、曲面拟合、支持向量机、BP神经网络等[9-11]。目前神经网络凭借其对非线性的映射能力,已经成为传感器性能补偿的主要方法之一。
本文在研究隧道磁阻传感器温度敏感机理的基础上,以隧道磁阻加速度计系统为研究对象,采用基于粒子群优化的自反馈Elman神经网络来构建其温度变化模型,从而对该加速度计进行实时有效补偿,提升了其温度性能。
1 隧道磁阻加速度计
1.1 基本组成
图1所示为隧道磁阻加速度计结构图,其由微悬臂梁、质量块和隧道磁阻等组成,通过力、磁、电多物理场耦合来实现加速度测量。
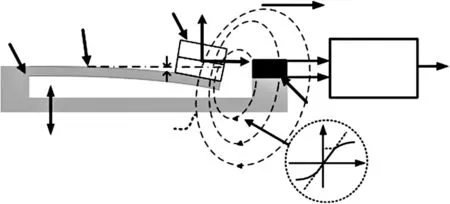
图1 磁阻微加速度计结构示意图
力场耦合方面:当外界加速度为a时,微悬臂梁会产生相应的形变,根据均布载荷模型可知加速度与自由端位移响应如式(1),从而可以将加速度线性转化成位移。
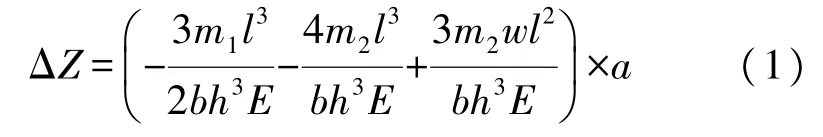
式中:E为杨氏模量,w为磁场源的长度,l为微悬臂梁的长度,m1为微悬臂梁质量,m2为磁场源质量,b为微悬臂梁的宽,h为微悬臂梁的高。
磁场耦合方面:悬臂梁自由端上永磁体位移的变化通过磁阻传感器可以将其转换为磁场变化,空间磁场分布如图2所示。磁场强度在Z轴方向上±150 μm位移范围内是线性变化,因此可以将位移线性地转换为磁场强度变化。为了保证一定的磁场强度大小,均衡参数后自由端位移范围两端仍存在小部分非线性,这对后续整体的磁阻加速度非线性产生了一定的影响。

图2 空间磁场分布
磁电耦合方面:通过隧道磁阻传感器将磁场强度的变化转换为电压的变化,再利用处理电路可以实现对目标信号的检测,最终的输出电压信号如下:

式中:Scantilever为微悬臂梁的灵敏度,Smagnet为磁场灵敏度,STMR为磁阻加速度的灵敏度,Gain为电路增益,a为加速度信号。
由式(2)可知,在微悬臂梁结构、磁场源以及磁阻传感器确定时,沿敏感方向上,实际输出电压V与输入加速度a呈线性关系。
1.2 温度特性
温度对隧道磁阻加速度计的影响主要体现在隧道磁阻传感器及微悬臂梁上。近年来,为了实现高灵敏度的隧道磁阻传感器,往往通过磁隧道结串联增加结面积来提高磁阻的变化率,但这不仅会使传感器噪声增加,同时会导致严重的工艺偏差,从而使其温度特性变差,因此温度是导致其精度变差的主要原因之一。根据文献[12]可知,磁隧道结的温度依赖性一般为负温度系数,在恒定电压V下,隧道电流和温度的关系可以用二次函数来表示。因此,隧道磁阻与温度对应关系如下:

式中:I(T)和I(0)分别为温度T和0K下的隧道电流,kB为玻尔兹曼常数,c为与势垒厚度和高度相关的常数。
由式(3)可知,随着温度的升高,隧道磁阻阻值下降,因此它不仅会对隧道磁阻加速度计的标度因子和零偏产生影响,同时还会影响其非线性。
硅微悬臂梁弹性模量随温度变化明显,根据文献[13]硅的杨氏模量温度模型表达式为:
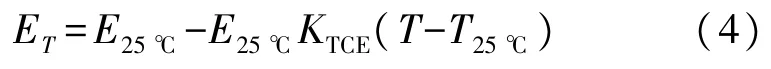
式中:ET、E25℃为分别对应在T温度和25℃硅的杨氏模量,KTCE为硅的杨氏模量温度系数,将式(4)代入式(1)可得:

由式(5)可知随温度的升高,杨氏模量也明显增大,在同等加速度的情况下,悬臂梁位移灵敏度将减小。因此这也会对标度因子和零偏产生影响。
2 温度补偿技术
2.1 磁阻传感器的温度误差模型及补偿
如图3所示,由于隧道磁阻传感器的内部是惠斯通电桥结构。根据文献[14]可知隧道磁阻大小由温度和磁场强度决定。将R(H,T)在H=0处泰勒展开,可得磁阻相对变化量,再根据电桥结构可以推导得出温度对磁阻传感器的输出造成的总误差:
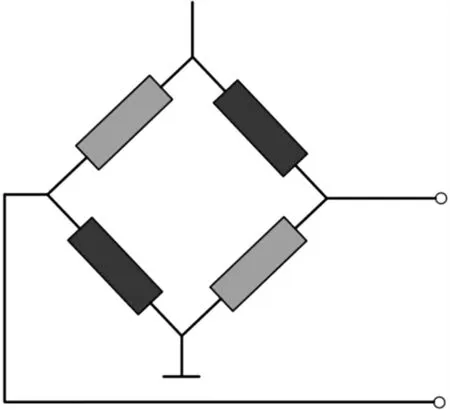
图3 惠斯通电桥结构

式中:Kt为灵敏度温度系数,ΔV为零位输出误差电压,ΔT为温度变化值,H为外界磁场强度,g1(·)为泰勒展开后近似的磁阻相对变化量函数、Vs为输入电压,a1、a2为桥臂电阻的比值系数,如式(7)、式(8)所示:

图4所示为磁阻加速度计及传感器输出的非线性,可知非线性一部分来自磁场耦合,另一部分来自磁阻传感器本身。

图4 磁阻加速度计及传感器输出非线性
图5为磁阻传感器在不同温度下的灵敏度,根据式(6)可以将对应温度点的误差量补偿至输出端,可得不同温度下加速度计的输出电压误差绝对值,如图6所示。

图5 不同温度下磁阻传感器灵敏度
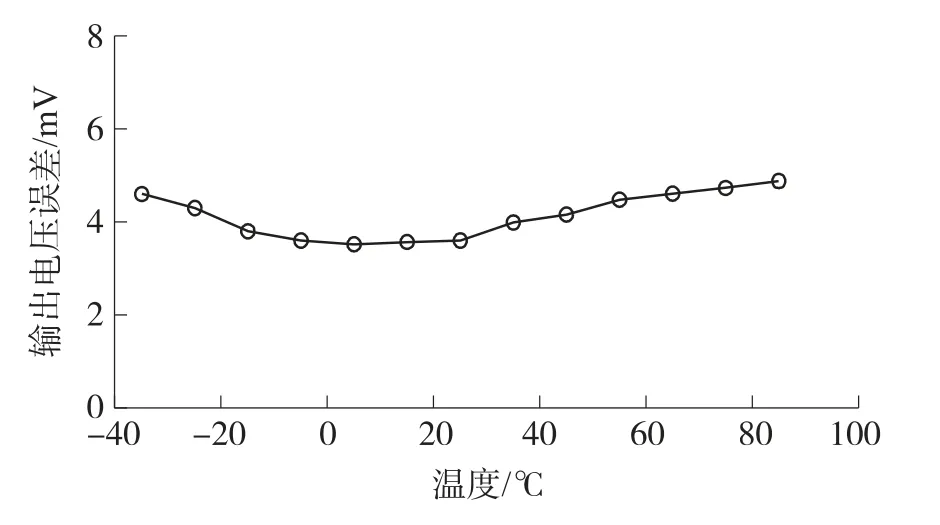
图6 输出电压补偿后的误差绝对值
由图6可知,通过误差函数的补偿,误差较大,精度不高,且存在两端温度点误差较大的问题。这是由于影响因素没有考虑完全,如微悬臂梁弹性模量,材料之间的热应力等。
由于磁阻加速度计系统温度影响比较复杂,不仅需要研究隧道磁阻的温度特性,还要对测量系统进行相关的智能补偿来提升性能。
2.2 自反馈Elman网络的加速度计系统温度补偿模型
Elman神经网络是一种经典的动态递归型神经网络,它可以有效地构建温度与加速度计输入、输出之间的模型。标准Elman网络仅仅与上一个时刻隐含层输出值有关,当动态系统大于1阶时,网络的预测精度便难以满足实际需求。因此可以在承接层中引入系数β来实现网络的自反馈,改进后承接层既可以自联至隐含层输出,又可以承载自身的历史数据,从而神经元对历史数据敏感度将大大提高,同时奇异值对整体网络的影响也可以有效避免[15]。网络数学模型如下:
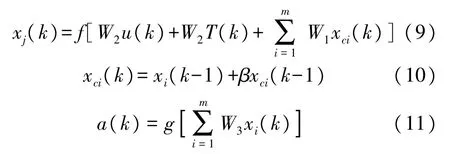
上式中,f(·)为隐含层的激励函数,g(·)为输出层的激励函数,m为承接层的节点数。
建立自反馈Elman经网络温度补偿模型。首先要确定网络结构,本文采用图7所示网络结构,输入信息为电压u和温度T,输出信息为加速度a。
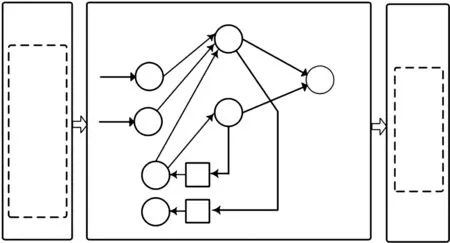
图7 网络结构模型
确定隐含层神经元个数。节点数将直接决定网络最终实现补偿的精度。因此,首先是通过经验公式(12)估算其大致范围,再利用训练样本数据对范围内的节点数分别进行训练,最终根据训练误差来获得最优的神经元个数。
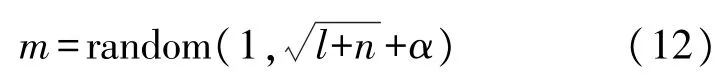
式中:m表示隐含层的节点数;l代表输入层的节点数;n代表输出层的节点数;α为0~10区间内的常数。根据式(12)可粗略估计节点数在1~12之间。根据实际计算量和预测误差,选择隐含层神经元个数为10时,均方误差较小。如表1所示,仿真的均方误差为4.7×10-4。

表1 仿真网络补偿模型的训练误差
在实际训练过程中网络的误差函数为均方误差(Mean Square Error,MSE)函数:

式中:为期望值;ak为实际值。根据误差E来不断修正,当误差E小于设定值时,网络训练完成,可得权值和阈值参数如式(14)所示:

由此可得加速度二维温度模型为:

式中:模型输出为加速度a(k),模型输入为加速度计电压输出u(k)和内部温度传感器输出T(k),g(·)为输出层线性函数,f(·)为隐含层S型转移激励函数。最终将该加速度二维温度模型写入补偿系统可实现实时的温度补偿。
2.3 补偿模型的优化
为解决Elman网络学习速度慢和局部最优的问题,采用粒子群算法(Particle Swarm Optimization,PSO)优化Elman网络,在求解迭代过程中,通过搜寻粒子个体极值点来获取群体极值点,并和历史全局最优解对比不断更新个体位置[16],最终获得满足停止条件的最优解。具体更新算法如下:
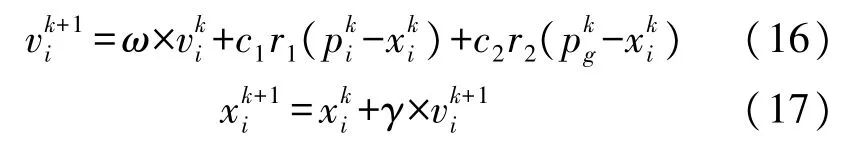
式中:ω为惯性权重;c1、c2分别为个体与社会学习因子,r1、r2为[0,1]区间内的随机数;γ为约束因子,xki和vki分别对应粒子i第k次迭代时的位置和速度,pki和pkg分别对应粒子i第k次迭代时个体极值点和群体极值点。
优化算法在MATLAB上实现,其中设置种群规模为80,最大迭代次数为150,个体与社会学习因子c1、c2取值为2。设置Elman网络的输入层为2,输出层为1,隐含层为10,最小均方误差为10-8,训练的次数为2 000,最终得到式(15)中对应的5组网络的权值和阈值,其具有全局最优的特点,这将有利于后续补偿模型的具体实现。
3 测试结果及分析
为了验证该补偿方法的可行性,根据式(15)的加速度二维温度模型,以实验室自研的隧道磁阻加速度计为目标对象,设计了温度补偿系统,实验测试系统及现场如图8所示。

图8 补偿系统及测试现场图
该系统以微处理器STM32F405为核心,包括数模转换和通信接口等。温度实验通过使用带温箱的双轴转台(2TS-450)来进行性能验证。将加速度计和温度补偿模块放置于温箱转台,经通信接口传输至PC机,并利用PC机端Labview采集程序获得最终输出结果。图9为温控转台测试系统框图。
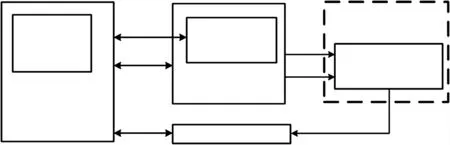
图9 温控转台测试系统框图
为验证该方法对加速度计的补偿效果,将采用全温实验获取隧道磁阻加速度计的非线性度NL、标度因子温度系数SFT、全温零偏极差ΔBias等参数[17]来进一步衡量。

通过全温实验,对比补偿前后加速度计的性能参数,可以验证算法构建的隧道磁阻加速度计温度模型的实际补偿效果。实验时通过测试程序来控制温箱温度,温度范围从-30℃至60℃,其中温度间隔为5℃;在每个温度点保温1 h后,控制转台从-2 gn升至2 gn,其中加速度间隔为0.5 gn。实验结果如表2所示。
由表2可知,补偿后,温度对隧道磁阻加速度计的影响显著降低,标度因子和零偏的波动得到显著的抑制,特别是在低温端时对标度因子的补偿效果明显。由图10(c)可知隧道磁阻加速度计的全温非线性度由3.038%减小为0.169%,表明该补偿方法对隧道磁阻加速度计的非线性有较大改善。

表2 补偿前后加速度计性能参数对比
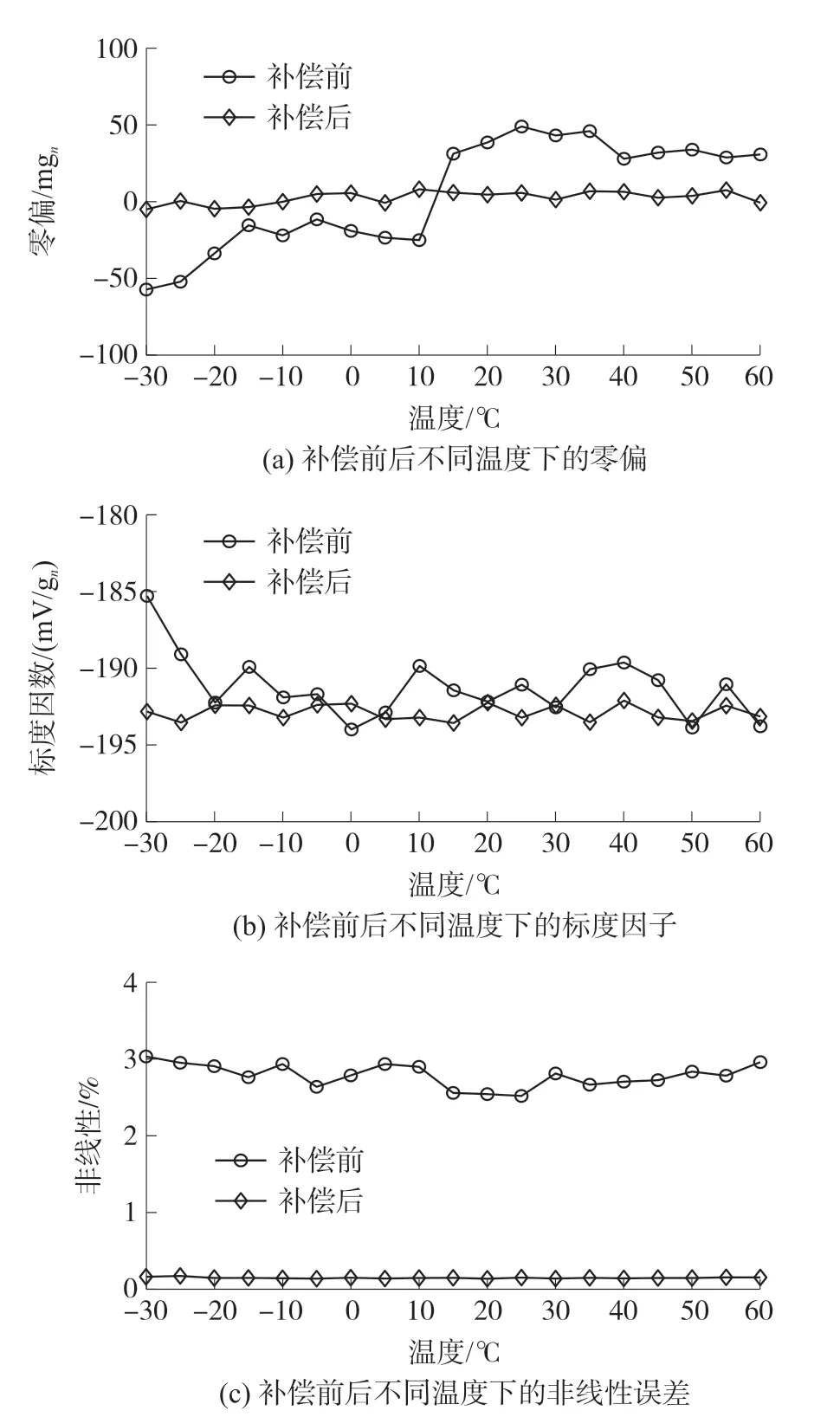
图10 补偿前后不同温度下的参数对比
为验证算法的全局最优性,实验测试-30℃~60℃下加速度从-2 gn以1 gn为间隔升高至2 gn的数据,计算各个数据点输出误差的绝对值。在图11(a)中,低温端的预测误差与其他温度点相比明显增大,而图11(b)中预测误差明显减小,这说明PSO优化后的自反馈Elman网络有更高的精度和较好的全局性。

图11 网络优化前后预测误差绝对值对比
4 结束语
本文在对磁阻传感器温度误差补偿研究的基础上,以隧道磁阻加速度计系统为对象,着重讨论了基于PSO优化的Elman神经网络的温度补偿方法与硬件系统设计。实验表明,隧道磁阻加速度计的标度因子温度系数从719×10-6/℃减小为183×10-6/℃,零偏极差由125 mgn减小为5.2 mgn,非线性度从3.038%减小为0.169%,隧道磁阻加速度计的温度特性得到较大的提升,证明了该方法的有效性,具有一定的工程应用价值。

