高效功率传输的电容参数超声换能器的设计与分析*
程义军,刘 畅*,薛晨阳,张斌珍
(1.太原工业学院电子工程系,山西 太原 030008;2.中北大学仪器科学与动态测试教育部重点实验室,山西 太原 030051)
超声换能器已经在各种应用中使用了许多年,如医疗成像,无损检测,无线电力传输和传感器[1-3]等。超声换能器分为压电式换能器和电容式换能器。早期的超声换能器由压电陶瓷或若干压电元件构成的复合阵列组成。随着20世纪90年代微加工技术的出现,电容式微机械超声换能器(CMUT)由于易于小型化、大带宽和易于电子集成的优点,在血管内超声成像,聚焦超声和能量传输等方面的应用日益突出[4-6]。
随着植入式医疗设备、物联网、可穿戴技术的出现,无线能量传输技术受到人们的关注[7-8]。尽管CMUT具有以上所述的优点,但是目前为止,超声无线功率传输的接收器均由压电换能器组成。这是因为压电换能器是一个完全无源的可自激装置,而电容式换能器需要一个直流偏置,这使得电容式传感器不太适合无线能量传输和能量收集应用[9-10]。而电容参数超声换能器(CPUT)可以克服这些限制。该换能器由一个时变的薄膜电容器与一个电感和电阻串联组成串联RLC电路。利用入射到膜上的两倍于RLC电路谐振频率的超声波驱动RLC电路进入参数共振状态,将声能高效地转换为电能[11-12]。与传统的电容式传感器不同,CPUT可以由热噪声激励启动,无需直流偏置,而且输入的超声能量直接转换为电能输出,不需要二次换能器。
与直接共振(在系统固有频率处施加力)不同,参数共振是一种电子或机械系统通过改变系统内部的某些参数而引起大振幅振荡的现象。参数共振是一种高度非线性的现象,因此在设计CPUT时需要进行详细的分析,以达到最佳性能[13]。本文提出了一种CPUT的一维模型,给出详细的公式推导,利用Simulink对其工作特性进行了仿真研究,通过研究不同参数对CPUT接收性能的影响,为高效能量传输CPUT的设计提供了理论基础。
1 建模
与许多在线性状态下工作的超声换能器不同,CPUT由于系统中存在固有的非线性而更加复杂,其性能参数,如声电转换效率,强烈依赖于诸如设备运行的介质、超声强度和频率、接收器动力学和负载电阻等因素。因此,在为特定应用设计CPUT时,要仔细考虑这些因素。
CPUT可以看作是一个由机械特性和电特性组成的黑盒。机械特性由一个时变电容组成,该电容在流体中受到入射超声场的激励。该电容器与电感和电阻串联在一起,形成RLC谐振电路。当电容在RLC电路谐振频率的两倍左右变化超过某一阈值时,系统被驱动进入参数谐振。此时,不断增长的电流在电路中产生,直到它被限制到一个由系统非线性和阻尼决定的稳态值。因此,入射波功率被转换成电能,然后通过负载电阻加以利用。
CPUT可以等效为一维集总参数模型,如图1所示。在该模型中,电容被等效为一个质量m、刚度k和阻尼b已知的平行板活塞。其质量和刚度值对应于流体负载活塞电容器的等效质量和刚度。阻尼表示在这种一维设置下,流体中的辐射损失和系统中的其他机械阻尼。这里假设电容器中的机械损耗与流体损耗相比是可以忽略的。

图1 CPUT一维集总参数模型
入射谐波超声力F0引起活塞在频率ωus以速度v进行振动。通过选择参数k和m,活塞的共振频率可以等于超声波频率ωus,该频率被称为机械共振频率ωom,其中

我们还定义了振动活塞的机械品质因素为

同样的平行活塞也作为一个时变电容,其电容值为

式中:d0是两个极板未振动时的间隙。该电容器与电感L和负载电阻R一起构成振荡器的一部分。为了有效地参数谐振,电感的取值可以选择使RLC电路的谐振频率为入射超声频率的一半,即ωus=2ωoel。其中ωoel是RLC电路的谐振频率,表示为

式中:C0为薄膜未振动时的电容。
一维集总参数模型也可以用数学方法表示为一个机械振荡器与一个电子振荡器通过时变活塞电容耦合。这可以用两个耦合的非线性常微分方程(Ordinary Differential Equations,ODEs)表示[14]。

式中:电容上的电压V和活塞的位移x是未知数。式(6)的右边表示作用在活塞上的力,它是施加在活塞上的超声力F0和通过电容的电压所产生的静电力的总和。
2 用Simulink作为一维模型的求解方法
通过在Simulink中建立RLC电路的最优数学模型,分析了一维集总参数模型的瞬态响应,Simulink电路实现如图2所示。由机械谐振和电路谐振两大部分组成。机械谐振主要是时变电容由传递函数模块表示,该模块以电容器电压和超声力为输入,提供平行活塞位移为输出。再通过活塞位移来确定瞬时电容,从而形成一个闭环。电路谐振主要是提供参数谐振的必要初始条件,在RLC电路中通过提供一个短的输入电压脉冲激励来产生谐振。然后对活塞表面施加均匀的超声力,如果超声力幅值超过一个要求的阈值,CPUT被驱动进入参数谐振,使用Simulink示波器可以记录电压、电流和位移等参数。

图2 一维CPUT模型的Simulink仿真原理图
3 数学公式的解析解
通过渐近分析,得到耦合非线性方程组的精确解析近似解[13]。当在Simulink中使用这些解析解时,通过提供稳态电压和电容上的位移以及驱动参数谐振的超声力阈值的表达式,可以更深入地分析CPUT的工作特性。这些表达式可以提供CPUT的操作限制,进而避免使用Simulink模拟大量案例的情况,提高仿真效率。
由于系统中的电阻损耗,为了驱动电路进入参数谐振,电容的变化必须超过某一最小阈值。获得有限稳态电压所需的最小超声力为:

从式(7)中可以看出,F0仅依赖于b、R、ωoel和A。在一维模型中,b完全依赖于工作介质,这意味着超声换能器在具有较低声阻抗的流体中工作时需要更小的超声力。同样的,在较低的频率下工作也减小了谐振激励所需的最小超声力。如果负载电阻R和电极面积A减小,CPUT对一个小的输入力也非常敏感。
4 结果
上述公式可以用于研究功率传输的CPUT性能分析,这主要取决于电气和机械参数的设定。为了进行详细的分析,我们定义了传感器的性能参数,并分析了液体环境中工作在2 MHz左右的CPUT的性能,如表1所示。

表1 典型CPUT所涉及到的参数
4.1 使用CPUT实例的参数化研究
使用表1中列出参数的CPUT来研究所开发的设备特性。假设CPUT是在人体组织内部工作,为植入物提供无线电源。由于水的特性非常接近人体组织的声学特性,因此确定水作为工作介质,超声波频率为2 MHz,活塞面积为1 mm2,这样设备占用空间小,可以在合理的水深范围内工作。选择k和m的值使机械谐振频率始终为2 MHz,电感L的值使电谐振频率始终为1 MHz。还必须注意的是,虽然为了达到仿真目的,输入超声强度在1 mW/mm2~15 mW/mm2之间变化,但是食品和药品管理局允许的诊断超声最大限度是7.2 mW/mm2。两极板之间有120 nm的间隙形成电容C0,选择电感L的值为340 μH和负载电阻R的值为50 Ω使得电路的无扰动谐振频率f0为1 MHz。利用这个理想模型,来研究参数谐振阈值行为,结果如图3所示。首先,当直接在平板活塞表面施加2f0的正弦力时,在电路上施加一个短的单极脉冲来激励初始振荡,模拟一个正常入射的超声力。本文用负载电阻上的电压来表示超声力大小对系统响应的影响。当超声力不足以产生参数谐振所需的电容变化时,振荡衰减,如图3(c)所示。随着超声力的增加,振荡持续时间变长。一旦满足参数谐振的准则,就会观察到电路中的电流随着超声力和负载电阻上的电压增长而达到稳定状态,如图3(d)所示。能量从输入的超声信号传递到负载电阻。系统中的非线性最终导致电压达到稳态值。
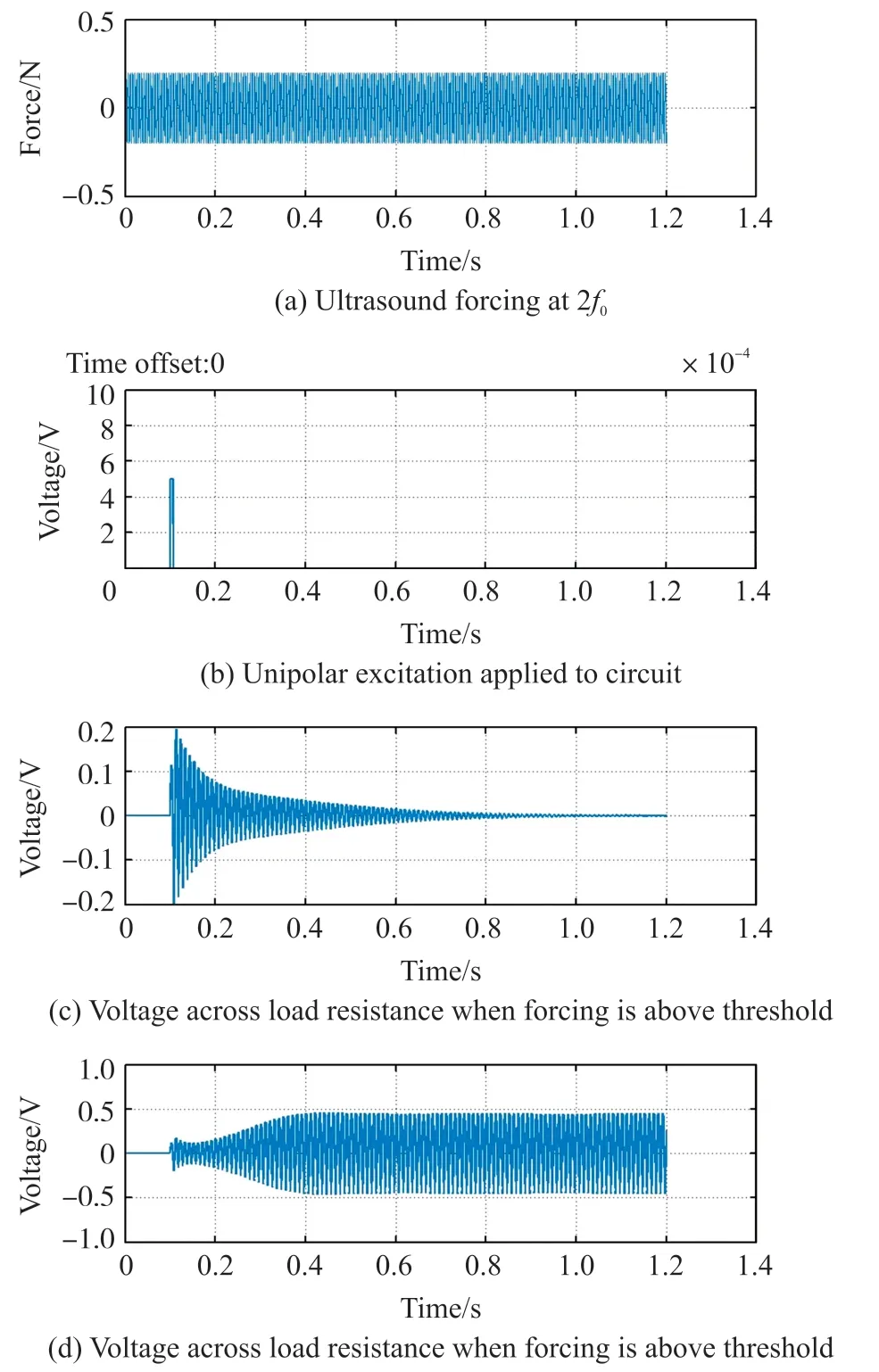
图3 超声力的阈值行为
在功率转换应用中,评价换能器的一个重要指标是CPUT的效率。使用Simulink仿真,效率可以计算为通过电阻耗散的平均功率与有效声功率的比值:

式中:i是电路中的电流,R是负载电阻。有效功率公式为(pA)2/Rf,其中p是在最佳阻抗匹配情况下活塞表面的声压,A是活塞面积,Rf是辐射电阻。为了保持一致,我们假设这个压力是由一个强度为I=p2A/Rf的入射波产生的。
4.2 负载电阻对声电转换效率的影响
CPUT的输入阻抗强烈依赖于负载的大小。假设一个纯实数负载,图4显示了2 MHz条件下,声电转换效率随负载电阻的变化情况。从图中可以看出,对于固定输入超声强度为3.33 mW/mm2(转换为1 mm2面积活塞上的力为0.1 N),在低负载电阻下,声电转换效率较小,但在60 Ω左右达到最大值,然后再次减小。增大负载电阻会导致输入电阻发生变化,获得最大效率时的电阻对应于CPUT与流体介质之间的最佳阻抗匹配。在负载电阻为100 Ω时,可以看到,由于超声力水平没有满足式(7)中定义的参数谐振所需的最小阈值,薄膜停止振荡,效率下降为0。通过增加输入超声强度,可以进一步提高临界负载电阻的上限。从图中也可以看出,增大输入强度等级,得到参数谐振的负载电阻范围也增大。同时也可以观察到,获得最大效率时的电阻向右移动,这意味着CPUT的输入阻抗取决于力的大小。
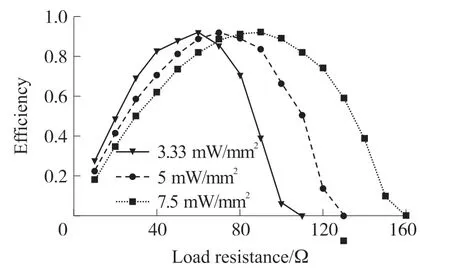
图4 不同输入强度下的效率
在固定电阻为60 Ω的条件下,通过改变输入超声频率和超声强度,研究了激励频率的微小变化对CPUT效率的影响。利用Simulink,从1 mW/mm2~15 mW/mm2的输入强度中获得了CPUT效率。超声频率ωus的值在2 MHz左右变化,以确定工作的频带宽度。从图5和图6可以看出,随着输入强度的增大,超声频率发生微小的变化,这是因为薄膜位移量增大,导致电容变化,进而引起频率的变化。利用图5可以预测CPUT的工作频率带宽,并跟踪参数谐振不持续的边界(用Simulink计算的零效率区域)。有趣的是,最大效率出现在略低于2ωoel的频率上。这可以解释为,当压力频率为RLC电路谐振频率的两倍时,系统被激励成参数谐振。然而,随着输入强度的增加,形成更大的电容器电压,反过来导致活塞上的平均吸引静电力更大,从而增加活塞平均位移。这使得电容器的电容从C0增加到C′0,因此电谐振频率略微降低至ω′oel。另外从图6也可以看出,增加输入强度会使CPUT的工作频率带宽变宽。因此为了以最大可能的效率运行CPUT,需要满足以下三点:①为一定的输入强度选择正确的负载电阻,以减少活塞表面的反射,提高声电转换效率;②为使CPUT更加有效地谐振,超声力频率必须稍失谐至ω′oel;③为了在更大的频率带宽上有效地操作CPUT,需要更大的输入强度。

图5 不同输入强度下的频率变化
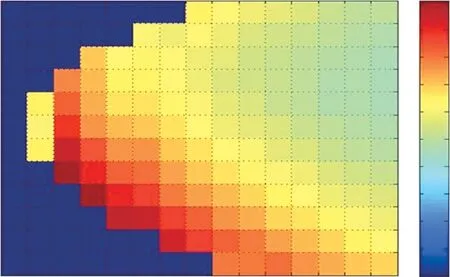
图6 不同输入强度和超声频率下的效率
4.3 电极覆盖面积和间隙高度对效率的影响
图7显示了在2 MHz条件下,对于面积为1 mm2、输入强度为3.33 mW/mm2的接收器,电极覆盖面积对CPUT效率的影响。CPUT的电极面积分别设置为1 mm2、0.5mm2和0.25 mm2,相应的电感值分别为343 μH、686 μH和1372 μH。可以观察到,对于相同的活塞面积,减少电极面积对CPUT的最大效率产生不可忽略的影响。当电极面积减小时,维持参数谐振所需的力减小。因此保持相同的力水平会导致临界负载电阻增加,并使最大效率点向右移。在基于活塞的CPUT中,平均位移小于等效平行板活塞的位移,因为当薄膜中心的运动范围较大时,靠近边缘区域不会移动那么多。通过将电极覆盖范围限制在中心高偏移区,可以补偿较低的平均位移,但仍然获得较高的效率。此外,在相同的工作频率下减小电极面积也增加了负载电阻的范围,这为匹配CPUT到更大范围的电阻负载提供了更多的灵活性。

图7 不同电极面积下的效率
在制备CPUT时,还需要考虑间隙高度选择的灵活性。如图8所示,在固定负载电阻为50 Ω、频率为2 MHz和输入强度为3.33 mW/mm2时,输出功率随间隙高度的变化而变化。可以看到,对于不同的输入强度,增大间隙高度均会导致输出功率逐渐减小。与之前情况不同,减小电极面积会增加临界电阻,而间隙高度没有这种影响。

图8 不同空腔高度下的输出功率
5 结论
本文提出使用一维集总参数模型来模拟CPUT在液体介质中的工作状态。利用Simulink对一维模型进行求解,并借助求解耦合非线性常微分方程得到的解析解,分析了CPUT的工作特性。使用一组示例参数,分析了负载电阻、工作频率、输入超声强度、电极面积和间隙高度对CPUT效率的影响。结果表明,为了达到一个最佳的效率,需要考虑两个最重要的因素:①确保CPUT的阻抗尽可能和介质匹配;②驱动CPUT工作的频率略低于2ωoel确保最有效的参数激励。
超声驱动参数谐振为机电换能器提供了一种不同的方法,电容换能器在没有直流偏置或永久电荷的情况下也可以工作。并且仿真也表明这样一个器件也可以被用于作为高效能量转换器。这为进一步研究利用CPUT在空气或水中进行能量传输提供了强有力的平台。

