基于改进狮群算法的管道传感器网络覆盖优化*

神显豪，马雪皎，牛少华，张烈平，谢晓兰

(1.桂林理工大学广西嵌入式技术与智能系统重点实验室，广西 桂林 514004；2.北京理工大学机电学院，北京 100081)

无线传感器网络[1](Wireless Sensor Network，WSN)是由大量的、低成本的传感器节点与具有通信、感测和计算能力的传感器节点部署在监控区域内部或外部的一种智能测控网络。各种应用在WSN中的新领域由于传感器节点成本的降低应运而生，并受到人们的广泛关注，其中包括在工业、商业、人体、军事、医疗保健等相关领域，以及面向管道检测的领域也有新的研究。通过无线传感器网络的节点部署技术对节点进行有效的部署，可以提高网络的覆盖率。将该技术应用到管道中，能够及时发现管道的缺陷，减少能源损失和降低维修成本。管道系统输送大量的液体和气体(例如石油、天然气、自来水、污水和化工产品等)，它是最经济的方式，与其他的运送方式(例如铁路、高速公路、船舶)相比，优点显而易见，具有成本低、运量大等优点，而且管道系统还是国民经济发展的基础设施。尽管它的优势特别明显，但随着管道长度的不断增加，对管道的检测和管理增加了许多压力，严重影响了管道安全和输送效率。无线传感器网络以其低成本、可持续、不间断、安全、高效的特点为管道系统提供监控和管理，极大地提高了管道系统的管理水平和经济社会效益[2]。

一旦部署了WSN，频繁更换传感器节点中的电源可能不可行或不经济。因此，在部署WSN的同时，最关键和最具挑战性的任务之一是有效地部署传感器节点，以使部署的网络是长寿命的、能耗最低的。WSN的主要研究挑战包括节点布局、覆盖、拓扑、路由、生存期优化和能源效率。Elnaggar等人[3]使用了受自然启发的技术，对专门用于石油管道监测的线性无线传感器网络进行节点布置和寿命优化。讨论了在给定传感器节点初始能量和消息缓冲限制的情况下，要部署的传感器的最佳数量问题。作者使用了两种进化算法来解决部署问题，即遗传算法(GA)和蚁群优化(ACO)。Kaur等人[4]使用混合元启发式技术为无线传感器网络设计节能协议。文献[5]提出了延长稳定选举协议(P-SEP)以在雾支持的WSN中的异构节点之间选举CH，以增加网络的寿命。文献[6]利用模拟退火技术通过最大化WSN的网络覆盖和寿命作为目标函数来控制拓扑。Laouid等人[7]设计了一种方法，根据每个传感器节点的跳数和剩余能量选择最佳路线，以最大限度地延长网络的寿命。文献[8]提出地下管道检测机器人传感器网络中传感器节点定位算法，网络由机器人携带的传感器节点和中继节点组成，用于信息感知和通信，通过考虑传感器节点的动力学，测量传感器节点的速度和地上中继节点接收到的无线电信号的强度，确定传感器节点的位置。

本文提出了一种基于改进狮群算法的管道传感器网络覆盖优化算法，该算法通过每次迭代获取所有传感器中的最优节点，并以每次最优解的节点为中心进行收敛，获取该范围内的最优解，从而更好地收敛到全局最优。本文考虑到多个管道，并且从多个不同的方向通过传感器节点将数据传送到基站，解决基站传输数据成功率的问题。该算法能够直接有效地应用于管理管道，并使用最少的节点数建立传感器网络，从而以安全、可靠的方式覆盖整个区域，并将数据传输到基站。为了解决传输数据的有效性问题，本文设计了一种基于狮群算法的节点部署优化方法，该方法使用最少数量的传感器节点，仍然可以覆盖最大面积，数据还可以以最小延迟传输到基站。通过仿真实验验证改进狮群算法部署优化能有效地解决数据传输问题，不仅延长了传感器网络寿命，而且还适用于长距离管道相互交叉的传感器节点部署问题。

1 管道部署模型

为了管道的安全并节省资源，需要建立一个传感器网络。设置传感器网络的主要目的是以某种方式沿着管道部署传感器节点，从而可以最大化网络寿命，将感应到的数据以最小延迟发送到最近的基站。场景设置在长度为L的管道，这些管道以纵横交错的方式放置，形成如图1所示的结构。在每个管道的两端均放置基站，传感器节点S(S1，S2，S3，…，Sn)部署在管道上。由于传感器节点在电池电量和范围具有一定的限制，因此，将这些节点利用改进狮群算法放置在可以最大程度地延长网络寿命和增加吞吐量，并可以减少端到端延迟的位置。由于管道通常是以直线铺设，标准管内直径为250 mm，而长度可以长达千米。本文针对直线铺设管道部署做出的假设条件:管道长度为L，节点通讯半径为R，网络规模为N(普通节点总数)，其中普通节点具有相同的初始能量、通信和计算能力。

图1 管道无线传感器网络部署模型

2 狮群算法分析及改进

2.1 狮群算法

狮群算法(Lion Swarm Optimization，LSO)的主要思想是[9]:从要优化的搜索空间的任意初始位置开始，将具有最佳适应性值的狮子作为狮子王，然后将一定比例的狮子选为狩猎狮子，它们合作狩猎。一旦发现更好的猎物，狮子王将会获得猎物的位置。幼狮与雌狮一起学习狩猎或者在狮子王附近觅食。当它们性成熟后，幼狮将被赶出群居，成为游牧狮子。为了生存，游牧狮子试图靠近它记忆中的最佳位置。因此，根据狮群的分工与合作，目标函数的最优值是由狮子不断搜索行为数据得到的。在狮群算法中，幼狮的行为增强了算法的局部优化能力，雄狮的捕食行为为该算法的全局收敛奠定了基础。

狮群算法的原理是:

假设在D维目标搜索空间中有N头狮子形成一个组，并且成年狮子的数量nLeader满足:

成年狮子的数量定义为:

式中:β是成年狮子所占比例因子。

在狩猎过程中，不同类型的狮子以不同的方式移动，而狮子王则在最佳食物区以较小的范围移动，以确保自己的特权并根据式(3)更新其位置。

式中:pki为第i个狮子第k代的历史最优，γ为正态分布N(0，1)产生的随机数，gk为第k代群体的最优位置。

雌狮需要在狩猎过程中进行协作，并根据等式(4)调整它们的位置。

式中:αf为雌狮移动范围扰动因子，pkc为从第k代雌狮群中随机挑选的一个捕猎协作伙伴的历史最佳位置，T为狮子群体中最大迭代次数，t为当前迭代次数，step为活动范围内移动的最大步长，为狮子活动空间范围内的最小值均值，为狮子活动空间范围内的最大值均值。

幼狮根据方程式(7)调整位置。

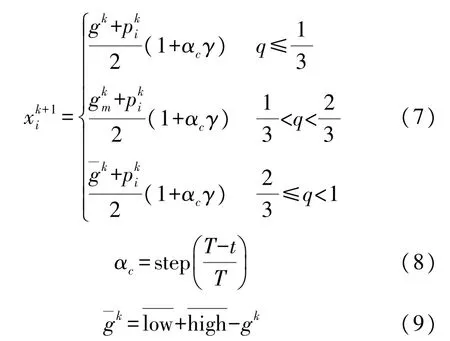
式中:αc为幼狮移动范围扰动因子，gkm为幼狮跟随雌狮的第k代历史最佳位置，q为均匀分布U[0，1]产生的均匀随机值，ˉgk为第k头幼狮被驱逐的位置。

2.2 改进狮群算法设计

狮群算法具有多种搜索方式和全局搜索的特点，但是狮群算法容易陷入早熟收敛。例如，在幼狮移动步长和雄狮捕食的移动步长中，由于它们的运行步长是固定值，会使算法过早地陷入局部优化，降低了算法的全局搜索能力，从而导致算法过早收敛。鉴于上述问题，从初始化、幼狮移动步长和雄狮捕食的移动步长三个方面进行狮群算法改进。

①初始化的改进

种群的初始位置对算法的收敛速度和精度有很大影响，甚至可能导致优化失败。在初始化过程中，搜索空间的随机分布会导致个体种群分布不均匀，多样性差。混沌映射是由确定性方程得到的具有随机性和遍历性的随机运动状态。因此引入sin映射混沌序列来初始化狮群的位置，加快算法的收敛速度。

②幼狮移动步长的改进

在基本的狮群算法中，幼狮靠自己的记忆向狮王移动时，使用固定的移动步长，这会降低算法的局部搜索能力和搜索方式的多样性，并使算法容易过早地陷入局部优化，因此，本文采用Logistic函数。Logistic函数是有界、连续、可导且严格单调，当x接近负无穷大时，y接近零；当x接近正无穷大时，y接近1；当x＝0时，y＝0.5。如式(11)所示。

幼狮靠自己的记忆向狮王移动时，随着距离的减小逐渐缩短游走的长度，缓慢地向狮王移动。通过Logistic函数，可以将运行步长转换为变量并映射到间隔(0，1)，使运行步长在(0，1)中减小，从而可以更准确地搜索最优解。改进幼狮移动步长如式(12)所示。

式中:Tmax为最大迭代次数，T为当前迭代次数。

③雄狮捕食的移动步长的改进

自然界中的许多鸟类会跟随Levy飞行，特别是在大空间中搜索目标且搜索者有限的情况下，Levy飞行是最有效的搜索方式之一。在狮群算法的捕食行为中，固定的捕食步长会降低算法的搜索能力。捕食初期的大步长用于寻找目标，从而扩大了搜索范围，避免算法陷入局部最优。捕食后期的小步长用于精确搜索，使在狮群中被驱赶出来的幼狮可以在小范围内搜索全局最优解。改进狮群算法(improved Lion Swarm Optimization，iLSO)的雄狮捕食行为移动步长如式(13)所示，式中运算符⊗表示张量积。

式中:Xi(T)为第i代雄狮捕食在第t代中的位置，Xbest(T)为当前雄狮捕食的最佳位置，s为Leavy飞行的随机步长，μ、ν符合正态分布，μ～N(0，σ2)，ν～N(0，1)。

雄狮捕食的移动步长是随机的，并且没有固定的大小和方向。在搜索迭代过程中，靠近局部最优解使得狮群算法容易跳出局部最优解，提高了最优解的质量，从而雄狮捕食行为增强了算法的搜索能力，奠定了算法全局收敛的基础。

2.3 改进算法复杂度分析

本文仿真实验针对相同的基准函数和WSN监测区域进行优化，为了简便计算，改进算法以种群规模N和最大迭代次数T作为时间复杂度标准。根据iLSO改进节点部署，引入Logistic函数和Levy飞行进行部署优化，增加了算法的时间复杂度为O(T×N)，因此，iLSO的最高时间复杂度为O(T×N)。

3 WSN覆盖优化

传感器节点的数量被认为是狮子的数量，狮子包括狮子王和流浪者。基站被认为是所有其他狮子(传感器节点)接近的猎物，管道的节点围绕着基站，距离基站最近的一个节点被认为是与基站直接连接的领导节点。当节点开始向基站传输数据时，狮子王开始进行狩猎行为。

假设管道的长度为L。任意给定长度中使用的节点数可由式(16)计算。此过程需要以2R的距离部署传感器节点，使网络即使在传感器节点出现故障的情况下仍然可以保持传感器连通。

式中:R为每个节点的通讯范围，MinNo_nodes为传输期间产生连接网络所需的最小节点数。通过使用放置在管道中距离为2×R的备份节点来完成。则有式(17)表示:

用于备份通信的备份节点。如果发生反向流动，则节点可能会改变其角色。附近的节点(领导节点)发送其信息并从不同节点发送大多数已接收消息的信息，发送的传感器的寿命取决于接收器附近节点的活力。同时，发送的节点受到支持空间很小的影响，无法访问备用空间，消息可能会被丢弃，因此接收器附近的节点会消耗大量的能量，所以志愿者节点被放置在接收器节点的附近。无线传感器网络中传感器节点定位优化的对应适应度函数可以由式(18)和式(19)表示。

式中:dist为节点到上一个节点的距离，delay为端到端的延迟，drop_ratio为丢包数与发送的包总数之比。以最小延迟和丢包率作为目标函数，把传感器节点以最大步长放置在不同长度的输油管道上进行部署优化。在两种情况下执行优化功能:一种是正常模式，另一种是在忽略邻居节点后的当前节点，两次拟合函数的平均值用作决策因子。

本文基于狮群算法，利用Logistic函数和Levy飞行，提出了一种基于狮群的无线传感器网络覆盖优化算法。该算法在管道上部署n个节点，通信范围为R，每端都有一个基站BS，基站和传感器节点位置将由所提出的算法决定。iLSO应用于传感器网络覆盖优化的目标为求解网络监测区域内传感器节点定位的最大值；输入为监测区域参数:管道长度L、传感器节点数n、通讯范围R等，以及iLSO参数:种群规模N、最大迭代次数T；输出为目标函数F最优适应度值以及dist、delay、drop_ratio。iLSO求解无线传感器网络覆盖优化的具体算法步骤如下:

Input:节点的数量n，通讯范围R Output:dist、delay、drop_ratio 1.计算网络中的节点数n＝L/(2R)2.初始化网络3.P′nodes＝Pnodes 4.初始化基站的位置PBS 5.计算dist、delay、drop_ratio 6.计算F F＝α1 dist ＋α2×delay＋α3×drop_ratio 7.从BS发送一条hello信号，no_of_leader＝确认收到信号的数8.if(no_of_leader＞1) Pavg＝∑Pnodes n P′nodes＝PBS＋rand×(Pavg-Pnodes) else P′nodes i＝Pnodes i rand＞pri RAND其他{ pri＝0.1＋min 0.5，(Pi-Bestpi)Bestp■■■■■■■■ i＝1，2，…， P′nodes＝P′BS＋rand×(Pavg-Pnodes) P′BS＝PBS＋rand×pri×(PBS-Pnodes)9.将数据从节点传输到BS，并计算dist、delay、drop_ratio 10.计算F′ F′＝α1 dist ＋α2×delay＋α3×drop_ratio 11.if(F′＜F) PBS＝P′BS Pnodes＝P′nodes 12.if(｜F′＜F｜＜0.01) end else go to step 3

4 实验仿真与结果分析

4.1 基准函数优化实验

为了验证改进狮群算法(iLSO)在无线传感器网络覆盖优化的有效性，从文献[10]中选择了2014 CEC竞赛的30套基准函数，基准函数如表1所示。本文通过MATLAB仿真，与六种启发式算法进行比较，包括入侵性杂草优化算法(Invasive Weed Optimization，IWO)[11]、基于生物地理的优化算法(Biogeography Based Optimization，BBO)[12]、重力搜索算法(Gravitational Search Algorithm，GSA)[13]、狩猎搜索算法(Hunting Search，HuS)[14]、蝙蝠算法(Bat Algorithm，BA)[15]、水波优化算法(Water Wave Optimization，WWO)[16]。

表1 基准函数表

为了保证测试实验的公平性，将IWO、BBO、GSA、HuS、BA、WWO和iLSO对每个基准函数均独立运行50次，取最优适应度的标准方差进行比较。同时，每个算法设置相同的种群规模N＝50、最大迭代次数T＝50和测试维度D＝30，并且将功能评估的最大数量设置为停止条件。表2描述了通过响应面分析法(Response Surface Methodology，RSM)调整提出算法的参数[17]。

表2 比较算法的参数值

在单峰基准函数条件下，从表3中可以看出，iLSO在函数f1、f2和f3上相比于其他的算法提供了更好的性能，对于函数f1已经取得了理论的最优值，而对于函数f2、f3性能表现的不显著，且相比其他对比算法也有较大程度的提高，更优的标准差值表明该算法具有更好的优化质量和鲁棒性。

表3 单峰基准函数标准方差比较结果

在多峰基准函数条件下，由于存在大量的局部最优，因此很难找到较好的解决方法，并避免局部最优。从表4中可以看出，iLSO表现出显著的性能，相比于其他几个算法，提供了更好的结果。iLSO对函数f4的收敛精度略高于BA，但相比其他对比算法有较大的提升，较小的标准差值也表明该算法具有较好的稳定性。

表4 多峰基准函数标准方差比较结果

在混合基准函数条件下，将变量随机分为一些子组件，然后将不同的基本函数用于不同的子组件，这会导致算法的性能显著降低。从表5中可以看出，iLSO对函数f17-f22的结果比其他算法都要好，iLSO的总体性能在这些基准函数上与其他算法显著不同，从图2中可以看出，iLSO在迭代不到10次时已经实现了收敛，表明改进后的算法能够有效提高算法混合基准函数的收敛速度。

图2 混合基准函数优化收敛曲线

表5 混合基准函数标准方差比较结果

在合成基准函数条件下，从表6中可以看出，iLSO在大多数性能上较好，但在f24、f28和f29上，iLSO的性能较弱，从图3中可以看出，iLSO在迭代不到20次时实现了收敛，表明改进后的方法能够有效提高算法合成基准函数的收敛速度。iLSO提升合成优化性能，从而对函数f25和f30均取得了其理论最优值。总而言之，iLSO在单峰、多峰、混合和合成函数上与其他六种启发式算法相比是最好的。

表6 合成基准函数标准方差比较结果

图3 合成基准函数优化收敛曲线

综上所述，通过在不同形态函数上的仿真优化结果，可以明显看出，改进狮群算法收敛精度更高、收敛速度更快和鲁棒性更好。

4.2 仿真结果与分析

将改进狮群算法与现有的不同算法进行了比较，本文通过MATLAB仿真，所考虑的参数已汇总在表7中，与蚁群算法(Ant Colony Optimization，ACO)[18]、遗传算法(Genetic Algorithm，GA)[19]和贪婪算法(Greedy Algorithm)[20]进行端到端延迟、吞吐量(单位时间内成功地传送数据的数量)和网络寿命(节点能量损耗——在网络中大部分节点不能提供信息时，此时将该区域的节点退出网络)的比较，与改进正弦余弦算法(Enhanced Sine Cosine Algorithm，ESCA)[21]、混沌优化细菌觅食算法(COBFO)[22]进行网络覆盖率的比较，充分验证改进狮群算法应用在无线传感器网络覆盖优化的有效性。实验中，设置iLSO的种群规模N＝30，最大迭代次数T＝50，每组实验独立运行50次，取第50次优化的节点情况进行对比结果展示。

表7 比较算法的参数值

图4和图5为iLSO节点部署和ESCA、COBFO节点部署的网络覆盖率比较。使用相同数量的传感器节点，与文献[21]、[22]的网络覆盖优化做比较，iLSO节点部署比ESCA、COBFO节点部署的网络覆盖效果要好，在相同网络覆盖率的情况下，管道的长度不同，则使用的传感器节点的数量不同，但iLSO算法使用传感器节点的数量最少。当管道长度为1 500 m时，iLSO覆盖率与其他两种算法的覆盖率差值最大，管道超过1 500 m，覆盖率的变化趋于稳定。

图4 网络覆盖率(节点通讯范围50 m)

图5 网络覆盖率(节点通讯范围100 m)

由于在ESCA节点部署优化和COBFO节点部署优化中，节点在管道中分布不均、节点冗余性和覆盖面重复较大，而改进狮群算法使无线传感器节点在管道监测区域中均匀分布，覆盖度大的节点几乎不产生节点冗余，并且覆盖率平均能够到99.08%，几乎没有覆盖空洞。当节点通讯范围为50 m时，通过改进狮群算法得到节点部署优化网络覆盖率提高了1.99%，当节点通讯范围为100 m时，通过改进狮群算法得到节点部署优化网络覆盖率提高了1.42%，传感器节点在管道监测区域中分布得更加均匀，重复覆盖的区域会更少，节点的冗余性也会降低，以此达到改进狮群算法优化覆盖的目的，并且该算法能够以较少的节点有效覆盖监控区域，从而节省节点置换成本并延长无线传感器的监控时间。

图6和图7中显示了iLSO与ACO、GA和贪婪算法之间端到端延迟的比较，从仿真结果可以明显看出，所使用的iLSO优于贪婪算法，并且表现出略好于GA和ACO的性能。当传感器节点的通信范围增加时，端到端延迟正在减小，这是因为传送数据分组所需的中间节点的数量减少了。贪婪方法的延迟随着管道长度的增加而增加，而在使用其他三种元启发式技术的情况下，这种趋势并不一致。这种现象的一个可能原因是，当管道长度增加时，节点的数量也会增加。

图6 端到端延迟(节点通讯范围50 m)

图7 端到端延迟(节点通讯范围100 m)

图8和图9中显示了iLSO与ACO、GA和贪婪算法之间吞吐量的比较。从仿真结果可以明显看出，iLSO算法在吞吐量方面优于贪婪算法。此外，iLSO算法在吞吐量方面略好于其他两种算法，即GA和ACO。在所提出的方法中，位置已根据丢包率和延迟进行了优化，这个因素是该算法吞吐量更好的原因。对于所有算法，随着传感器节点通信范围的增加，吞吐量都会增加。虽然随着管道长度的增加，吞吐量呈现上升趋势，但是iLSO算法的吞吐量最大，当管道长度为1 500 m时，吞吐量趋于稳定。

图8 吞吐量(节点通讯范围50 m)

图9 吞吐量(节点通讯范围100 m)

图10和图11中显示了iLSO与ACO、GA和贪婪算法之间网络寿命的比较。从仿真结果可以明显看出，在每种情况下，iLSO具有不同管道长度的网络寿命要好于ACO、GA和贪婪算法。当管道长度为1 500 m时，iLSO网络寿命与其他两种算法的网络寿命差值最大，管道超过1 500 m，网络寿命的变化也在增大，不过变化的趋势在减小。当管道长度为1 500 m时，其性能明显优于其他三种算法，因此iLSO适用于较长的管道。

图10 网络寿命(节点通讯范围50 m)

图11 网络寿命(节点通讯范围100 m)

当增加传感器节点的通信范围时，对于所有算法，网络寿命都会略有增加。尽管每个数据包消耗的能量与传感器节点的通信范围成正比，但是由于中间节点数量的减少，传输数据包的总能量需求减少。因此，归一化网络寿命在增加传感器节点的通信范围时显示出改善。综上所述，通过在不同性能上的比较，验证了iLSO覆盖优化的有效性及优越性。

5 结论

本文提出了一种改进算法，该算法通过改进狮群算法来建立相互交叉管道的传感器网络。将不同长度的管道用改进狮群算法与其他启发式算法相比较，传感器节点在采用改进狮群算法的管道上具有更好的网络覆盖、端与端之间的延迟、网络寿命和吞吐量。从仿真结果可以看出，改进狮群算法在性能和传感器网络覆盖优化的有效性上得到了更好的验证，当管道长度为1 500 m时，其性能明显优于ACO、GA和贪婪算法，因此该算法适合用于较长距离的、相互交叉的管道中传感器网络节点的部署。