复杂环境下针对遮挡目标的鲁棒自动跟踪方法*
石义芳,方伟业,周福珍,郭云飞
(杭州电子科技大学自动化学院 通信信息传输与融合技术国防重点学科实验室,浙江 杭州 310018)
复杂环境下的目标自动跟踪技术通常面临高目标漏检、密集杂波干扰等挑战,跟踪系统不仅需要估计目标的动力学状态,还应对大量身份未知的航迹进行自动管理,包括起始并维持目标航迹[1]、识别并剔除虚假航迹。目标自动跟踪技术已被广泛应用于智能监控、汽车辅助驾驶、精确制导等领域[2-3]。数据关联[4]是解决测量来源不确定的有效手段,基于数据关联的目标自动跟踪方法可分为单帧和多帧目标自动跟踪两种。综合概率数据关联算法[5-6](Integrated Probabilistic Data Association,IPDA)是一种经典的单帧目标自动跟踪方法,该方法利用概率数据关联(Probabilistic Data Association,PDA)的思想实现当前帧测量与航迹的数据关联,通过递归计算目标存在概率[7](Probability of Target Existence,PTE),对航迹质量进行打分,并实现对未知身份航迹的自动管理。然而,该类方法在高目标漏检、密集杂波干扰环境下的数据关联准确性急剧恶化。而多帧自动跟踪方法通过保存每条航迹的历史关联假设信息,利用后续实时观测不断加强数据关联的准确性。多假设目标跟踪方法[7-8](Multiple Hypothesis Tracking,MHT)通过穷举航迹分支与观测的关联假设获得最优的数据关联性能,然而该方法的计算复杂度随着杂波密度、航迹分支数的增加呈指数增长。综合航迹分裂(Integrated Track Splitting,ITS)[9-10]是一种兼顾数据关联准确性与计算复杂度的多帧目标自动跟踪方法,该方法仅利用当前时刻航迹分量与高质量观测的枚举关联,有效解决了关联假设个数爆炸式增长的问题,同时利用PTE对未知身份航迹进行高效的自动管理。
遮挡目标的跟踪问题一直是国内外研究的重点和难点,能否有效地处理遮挡,特别是严重遮挡,是评判一个目标跟踪算法鲁棒性的重要依据。线性预测[11]基于轨迹预测目标位置,该方法实现简单且能够处理短时间的目标遮挡,但当目标运动状态发生机动或目标长时间被遮挡时,线性预测跟踪往往会失效。Musicki D教授[12]提出的遮挡目标下的综合概率数据关联(IPDA-Occlusion Target Tracking,IPDA-OTT),考虑了目标存在但无法被观测的可能性,在稀疏杂波环境下有着不错的跟踪性能。然而,在目标漏检、密集杂波干扰复杂环境下,上述方法对遮挡目标的跟踪性能快速恶化。为此,针对严重遮挡目标的鲁棒自动跟踪问题,对现有的ITS方法进行改进。通过对遮挡目标的存在事件进行三状态建模,在现有ITS多帧数据关联的基础上,对每条航迹的航迹分量进行扩充关联,同时考虑目标存在且可观测和目标存在但不可观测的可能性,重新推导了目标三状态下的航迹分量关联概率,实时递归计算每条航迹分量跟踪目标航迹的概率,并以此完成对未知航迹的自动管理。
1 问题描述
本章探讨复杂环境下,基于ITS的目标自动跟踪方法所需的系统模型,包括目标存在状态、目标动力学状态以及传感器量测模型。
1.1 目标存在状态模型
在监视区域内,tk时刻目标的存在性和位置都是未知。现有的ITS只考虑目标存在状态的两种可能性,即:目标存在与目标不存在两种状态,目标存在事件与目标不存在事件构成完备事件组:
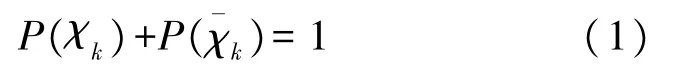
式中:χk表示tk时刻目标存在表示tk时刻目标不存在。
目标存在概率[13]的演化通过下式获得:

式中:M1表示目标二状态转移矩阵。以P(χk|χk-1)为例,P(χk|χk-1)表示tk-1时刻目标存在而且在tk时刻目标依然存在的概率,可由下式计算:

式中:Tχ表示监控区域内目标的平均寿命,Δtk表示tk-1时刻到tk时刻的时间间隔,通常Δtk≪Tχ。
1.2 目标运动模型
通常情况下,tk时刻二维笛卡尔坐标系的目标状态向量Xk可表示为:
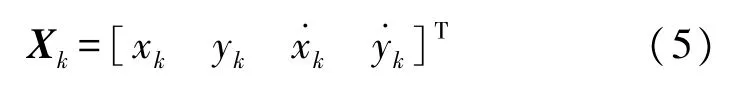
式中:xk和yk分别表示tk时刻笛卡尔坐标系中的位置信息,和分别表示tk时刻笛卡尔坐标系中的速度信息。由于在实际应用中,传感器的采样周期很小,目标在采样周期时间内可近似为匀速直线运动。因此,采用近似匀速直线运动模型具有合理性,以常用的匀速直线运动模型为例,其动力学状态时域演变模型表达式为:
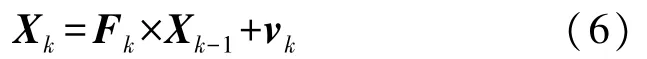
式中:Fk为tk时刻目标的状态转移矩阵,vk~N(0,Qk),Qk为过程噪声协方差矩阵。
1.3 传感器观测模型
假设传感器的分辨率无限大且目标为点目标,即:每个量测有且仅有一个来源(杂波或目标)。根据采样周期,传感器每时刻都会产生一个量测集,该量测集内可能会包括目标量测以及任意数量的杂波量测。令Zk表示传感器在tk时刻得到的量测集,Zk(i)表示Zk中第i个量测,Zk表示传感器从第一个时刻累计到tk时刻的总量测集。

传感器在探测过程中,当目标存在时,目标以一定的概率PD被检测到,tk时刻目标位置量测Zk(i)可根据目标状态方程建模得到。

式中:Hk为量测矩阵,本文假设传感器的量测形式是线性的,wk~N(0,Rk),Rk为量测误差协方差矩阵。
在tk时刻,当目标不存在或者目标被遮挡时,那么传感器无法探测到目标量测zk,此时zk={}。除了目标量测,传感器在每一时刻会返回任意数量的杂波量测。通常在监控区域内,杂波量测的状态在空间上服从均匀分布,在时间上服从泊松分布。
在复杂环境(密集杂波、高目标漏检)下,并且目标伴随着不同时长的遮挡,本文将利用传感器在tk时刻返回来源不确定的量测集Zk,探究复杂环境中遮挡目标的鲁棒自动跟踪方法,实现快速起始并鲁棒维持目标航迹、识别并剔除虚假航迹,精准估计目标的动力学状态。
2 综合航迹分裂法
针对单帧目标自动跟踪方法在高目标漏检和密集杂波干扰下因数据关联准确率下降而导致目标自动跟踪性能恶化的问题,Musicki D教授提出了一种兼顾数据关联准确性与计算复杂度的多帧目标自动跟踪方法-综合航迹分裂法(ITS)[9]。该方法通过利用当前时刻航迹分量与高质量观测的枚举关联,有效解决了关联假设个数爆炸式增长的问题,同时利用PTE对未知身份航迹进行高效的自动管理。由于所提方法主要在现有ITS基础上针对复杂环境下遮挡目标的鲁棒自动跟踪问题进行改进,因此有必要对现有的ITS方法进行回顾。为节省篇幅,下文仅介绍现有ITS与本文所提方法的不同之处:航迹目标存在概率和航迹状态更新两方面,ITS算法的完整介绍参见文献[9]。
在ITS中,目标在tk时刻的航迹混合状态由目标存在事件χk、目标动力学状态Xk(下文统称为航迹状态)构成,其中,χk为随机离散变量,Xk为随机连续变量,ITS在每个tk时刻递归地计算每条航迹的混合状态概率密度函数(Probability Density function,PDF),其数学描述为:

2.1 目标存在概率更新
每条航迹的目标存在概率P(χk|Zk)更新计算公式如下[9]:
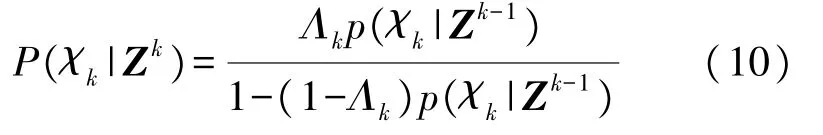
式中:p(χk|Zk-1)为tk时刻目标存在概率预测,由式(2)计算得到,Λk为观测似然比。
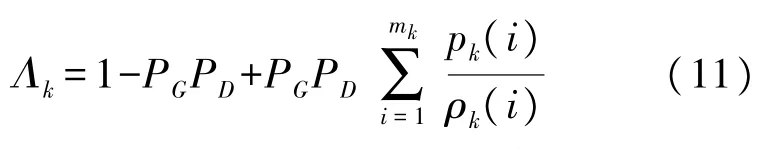
式中:PG表示目标量测落入波门的概率,ρk(i)表示tk时刻门限量测zk,i的杂波密度。每条航迹的每个航迹分量均独立地进行门限量测,mk表示tk时刻该条航迹所有航迹分量门限量测集合的基数。pk(i)为zk,i相对于该条航迹的似然值,其为所有航迹分量门限到该量测似然值的加权融合,计算如下:

式中:p(ck-1)为该航迹的航迹分量ck-1的相对概率,且满足表示zk(i)对应航迹分量ck-1的观测似然值,其计算如下:

2.2 航迹状态更新
在ITS中,航迹状态的更新由航迹在tk时刻新生成的各航迹分量后验状态估计的加权融合得到,其计算如下[9]:
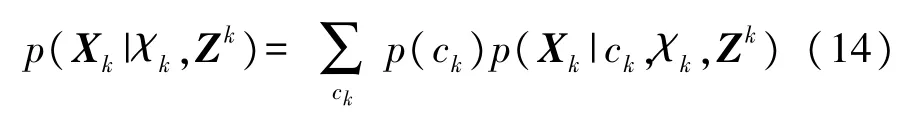
式中:ck表示新生成的航迹分量,其为该航迹在上一时刻的航迹分量与其在当前时刻门限量测的关联组成,即,ck={ck-1,zk(i)}。p(xk|ck,χk,Zk)表示航迹分量ck后验状态估计,其分布服从高斯分布,均值及对应方差由标准KF滤波更新得到。p(ck)表示tk时刻航迹分量ck的相对概率,其更新计算为:
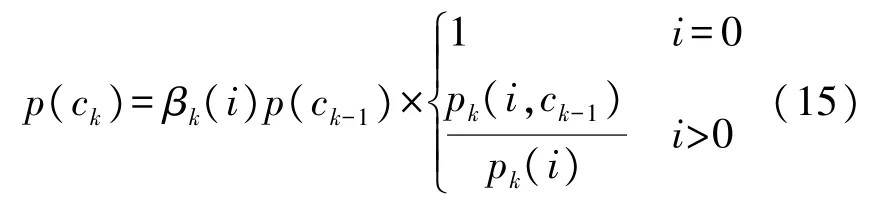
式中:βk(i)表示门限量测zk(i)与航迹的关联概率,其计算如下:
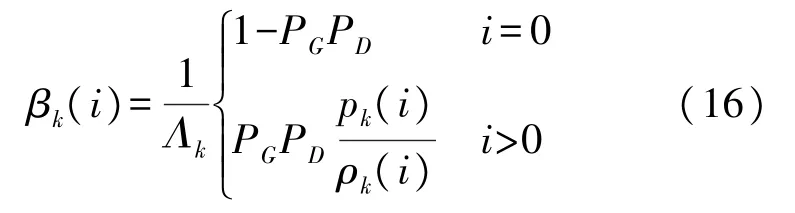
ITS是一种基于多帧数据关联的自动跟踪算法。每条航迹拥有多条航迹分量,每个分量独立进行关联假设,通过后续量测不断形成新的航迹分量。为了避免关联假设数爆炸式增长的问题,ITS仅针对门限内的确认量测进行关联,同时,采用航迹分量合并与裁剪的方式及时剔除新生成航迹分量中的低质量分支。完成每条航迹的混合状态递归更新后,首先利用更新的目标存在概率对身份未知的航迹进行高效管理,起始目标航迹,再输出目标航迹的后验状态估计。
3 改进的综合航迹分裂算法
ITS虽然能在高目标漏检、密集杂波干扰等复杂环境下有效地实现对目标的自动跟踪,但当目标被遮挡时,ITS并未考虑目标存在但不可观测这一情况,导致在遮挡区域的目标自动跟踪鲁棒性急剧下降,目标航迹连续性变差,甚至出现失跟现象。因此,本章针对复杂环境下的遮挡目标自动跟踪问题,对现有的ITS方法进行改进,提出了改进的综合航迹分裂法(Enhanced ITS,EITS)。
EITS递归地计算每条航迹的混合状态概率密度函数p(xk,χk|Zk),其数学描述同式(9)。区别于现有的ITS,本文所提EITS方法针对复杂环境下的目标遮挡问题,对目标存在事件进行三状态描述并构建其时域演变模型,在此基础上,重新推导航迹混合状态中目标存在概率、航迹状态的更新过程。为了避免重复,下文仅对EITS中的目标存在事件描述与建模、目标存在概率更新、航迹混合状态更新这三部分内容进行阐述,算法的其他步骤与现有ITS保持一致。
3.1 目标存在事件三状态描述与建模
当目标被遮挡时,目标在监控区域中虽然存在,但相对传感器仍然不可观测。针对遮挡目标这一特殊问题,EITS对目标在tk时刻的存在事件进行三状态描述:目标不存在,目标存在且可观测χok,目标存在但不可观测χnk,该三状态构成完备事件组:
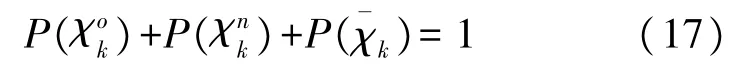
式中:χok和χnk为目标存在条件下的两个互斥事件:

与ITS类似,目标存在事件三状态的时域演变符合一阶马尔科夫链模型[14-15]:
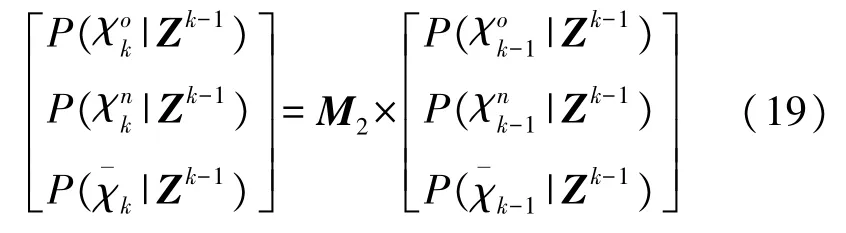
式中:M2为转移概率矩阵,

3.2 基于目标存在三状态的目标存在概率更新
在tk时刻更新的目标存在概率P(χk|Zk)由两部分组成:

式中:P(χok|Zk)表示目标存在且可观测的后验概率,P(χnk|Zk)表示目标存在但不可观测的后验概率。经过的复杂公式推导(详见附录),航迹在tk时刻更新的目标存在概率为:

式中:δk=1-Λk,δk由附录中式(41)得到,P(χok|Zk-1)和P(χnk|Zk-1)分别表示目标存在且可观测预测概率、目标存在但不可观测预测概率,由下式得到:

式中:P(χok,ck-1|Zk-1)和P(χnk,ck-1|Zk-1)分别表示隶属于该航迹的航迹分量ck-1的目标存在且可观预测概率、目标存在但不可观预测概率,由3.1章节中构建的目标存在三状态时域演变模型得到:

式中:P(χok-1,ck-1|Zk-1)和P(χnk-1,ck-1|Zk-1)分别为航迹分量ck-1在上一时刻tk-1的目标存在且可观测后验概率、目标存在但不可观测后验概率。
3.3 基于目标存在三状态的航迹状态更新
在tk时刻更新的航迹状态利用Chapman-Kolmogorov方程展开如下:
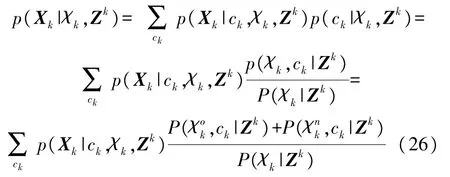
式中:p(xk|ck,χk,Zk)表示由ck-1新生成的航迹分量ck后验状态估计,其分布服从高斯分布,均值及对应方差由标准KF滤波更新得到。P(χok,ck|Zk)和P(χnk,ck|Zk)分别表示新生成的航迹分量ck在tk时刻的存在且可观测的后验概率、存在但不可观的后验概率,其更新由下式得到:


4 仿真验证
本章将在目标漏检、密集杂波干扰的复杂环境下,验证所提的EITS对遮挡目标自动跟踪的鲁棒性,同时,与现有的IPDA、ITS以及IPDA-OTT算法比较,最后测试所提EITS在目标不同遮挡时长下的自动跟踪极限。
4.1 仿真场景及参数设置
如图1所示,当飞机处于比较低的高度时,由于高山或高大建筑物的遮挡,雷达的视线就有可能被这些物体挡住,雷达电波无法穿透大山或高大建筑物,从而看不到远处的飞机,造成目标被遮挡的情况。雷达通过发射脉冲与回波脉冲之间的时间差测量距离,利用天线收到的回波信号幅度值来做角度测量。本文采用的传感器为地基预警雷达,其检测的信号为距离和角度,为了便于计算,在进行滤波之前,利用文献[16]详细给出了将极坐标系下的量测转换到笛卡尔坐标系下,同时对转换后量测值的协方差矩阵进行估计。

图1 算法应用场景
二维笛卡尔坐标系下,假设目标在检测区域[-100 m,1 300 m]×[-100 m,1 300 m]内做近似匀速直线运动。初始状态X0=[0 m 0 m 5 m/s 5 m/s]T,tk时刻过程噪声的协方差矩阵Qk中的光率谱密度q取0.01。传感器始终位于[-100 -100]m,传感器的采样周期T=1 s,检测概率PD=0.9,观测过程噪声协方差矩阵其中I2×2为2×2的单位矩阵,02×2为2×2的零矩阵,r为测距的一倍标准差,r取10。蒙特卡洛次数N=200,每次实验仿真时长为250 s。
仿真场景1:监视区域内的杂波密度为5×10-5个/m2。设置3、5、10、15 s的遮挡时长,仿真场景1中目标真实运动轨迹如图2所示。

图2 仿真场景1目标真实运动轨迹图
仿真场景2:监控区域内的杂波密度与仿真场景1中相同,设置20、25、30 s的遮挡时长。仿真场景2目标真实运动轨迹如图3所示。

图3 仿真场景2目标真实运动轨迹图
四种算法均采用二点初始化,最大约束速度设置为15 m/s。波门概率Pg=0.999,跟踪门门限g=13.816。多帧目标自动跟踪算法中的航迹分量剪切门限τ=0.05。在两种场景的航迹管理模块中,航迹的确认门限设为0.98,航迹终止门限为航迹初始概率的一半;通过调整航迹初始概率使各算法的虚假航迹个数接近一致,从而对比各算法在目标航迹起始与维持方面的性能。
基于二状态、三状态的目标存在状态转移矩阵M1和M2的分别为:

4.2 性能评价指标
为了验证所提算法在复杂环境下的遮挡目标自动跟踪性能,采用均方根误差(Root Mean Square Error,RMSE)、平均确认航迹个数(Averaged Number of Confirmed True Tracks,ANCTT)、航迹零碎度、目标航迹占比率四个指标对跟踪算法性能进行综合评价。其中,ANCTT、航迹零碎度、目标航迹占比率评价跟踪算法在目标航迹起始与维持方面的性能,RMSE评价跟踪算法在目标状态估计精度方面的性能。RMSE与ANCTT的定义以及计算公式可见文献[17]。航迹零碎度f衡量跟踪算法输出的目标航迹的连续性,其计算公式为:

式中:fi表示第i次蒙特卡洛实验跟踪算法输出的目标航迹数量。目标航迹占比率用来衡量跟踪算法输出的目标航迹存活时长,第i次蒙特卡洛实验中目标航迹占比率计算公式为:
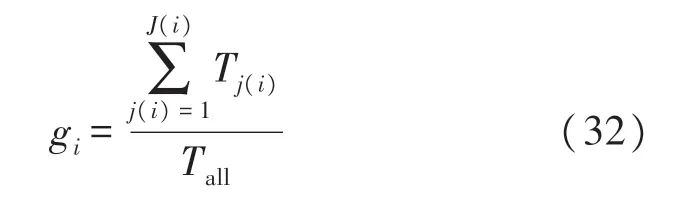
式中:j(i)表示第i次蒙特卡洛实验中第j(i)条跟踪目标的航迹。J(i)表示第i次蒙特卡洛实验中跟踪目标的航迹数量,Tj(i)表示第i次蒙特卡洛实验中第j(i)条航迹跟踪目标的时间,Tall表示目标存活周期。
4.3 仿真结果及分析
4.3.1 仿真场景1
通过调整初始PTE,使四种算法在所有蒙特卡洛实验中起始的虚假航迹个数维持41左右。图4展示了位置量测RMSE和四种算法位置估计RMSE的对比图,四种算法在目标被遮挡阶段均出现了RMSE性能下降,目标被遮挡的时长越长,其RMSE性能越差。从图中可以看出相比其他算法,EITS能保证良好的估计精度。图5展示了四种算法的平均确认目标数ANCTT,由图可知,四种算法均能快速识别并起始目标航迹,然而,当目标被遮挡时,基于目标存在二状态的ITS和IPDA因未考虑目标存在但不可观的情况,导致其在遮挡段的目标航迹维持性能下降,严重遮挡时,甚至出现完全失跟的现象;而IPDA-OTT和EITS由于额外考虑了目标存在但不可观这一特殊情况,其在遮挡段的目标航迹维持性能非常鲁棒,明显优于现有的IPDA和ITS算法,在目标被严重遮挡阶段,IPDA-OTT的目标航迹维持性能下降甚至失跟,而EITS依然能鲁棒地跟踪目标。
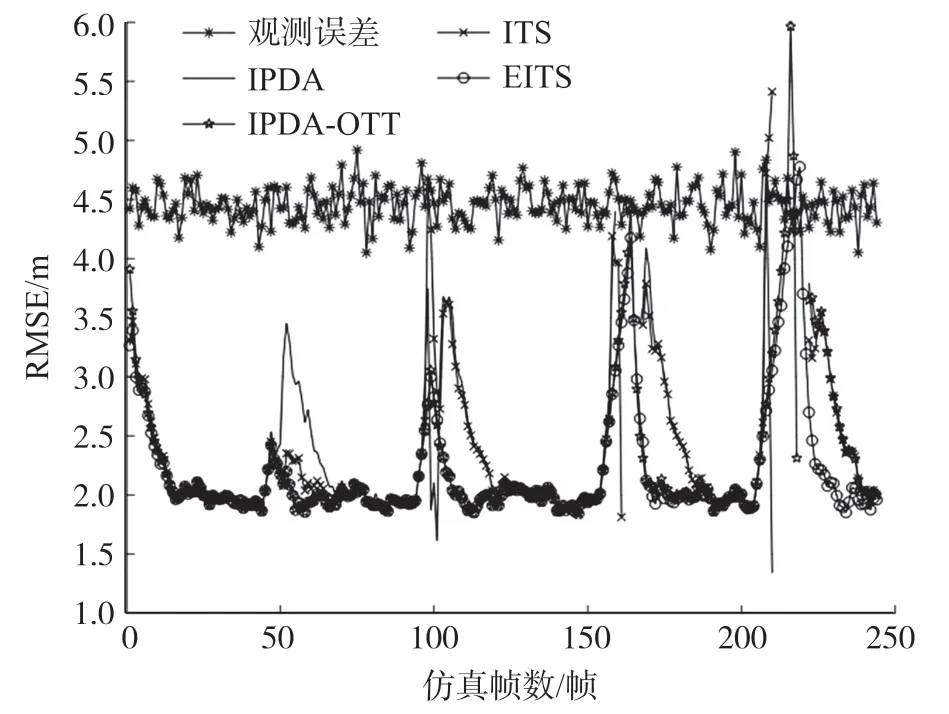
图4 位置的观测误差和估计误差比较图

图5 平均确认目标个数比较图
表1和图6分别展示了四种算法的航迹零碎度、目标航迹占比率,通过数据对比可知,基于目标存在三状态的IPDA-OTT与EITS的航迹连续性、目标航迹存活时长明显优于现有的IPDA与ITS。

表1 航迹零碎度

图6 航迹占比率比较图
4.3.2 仿真场景2
通过仿真场景1的验证可知,现有的IPDA和ITS算法由于未考虑目标存在但不可被观测的情况,在目标被遮挡时,其自动跟踪性能的鲁棒性急剧下降,而基于目标存在三状态的IPDA-OTT与本文所提的EITS方法仍然具备良好的遮挡目标航迹维持能力。因此仿真2着重比较EITS和现有的IPDA-OTT在目标被严重遮挡情况下的自动跟踪性能,同时测试EITS的跟踪极限。通过调整初始PTE,使两种算法在所有蒙特卡洛实验中起始的虚假航迹个数维持41左右。
图7展示了IPDA-OTT和EITS起始的平均目标航迹数,可以看出,两种算法均能快速识别并起始目标航迹。当遮挡时长为20 s时(目标被连续遮挡20帧),EITS的ANCTT性能远远高于IPDA-OTT,这是因为,IPDA-OTT是一种基于单帧数据关联的遮挡目标自动跟踪算法,当目标被长时间遮挡时,由于未能保留关联历史假设导致关联准确率急速下降,而本文所提的EITS是一种基于多帧数据关联算法改进的遮挡目标自动跟踪方法,以航迹分量形式保留的历史关联假设具备对长时间遮挡目标航迹的鲁棒维持能力。然而,当遮挡时长达到25 s时(连续遮挡25帧),EITS和IPDA-OTT均开始失效。由表2和图8可知,本文所提EITS的目标航迹连续、存活时长明显优于现有的IPDA-OTT算法,进一步验证了所提方法较现有遮挡目标自动跟踪算法的优越性。

图7 平均确认目标个数比较图

表2 航迹零碎度

图8 航迹占比率
5 结论
本文探讨了复杂环境下针对遮挡目标的鲁棒自动跟踪算法研究,针对遮挡目标存在但不可被观测这一特殊问题,对目标存在事件进行三状态描述,并构建了基于一阶马尔科夫链的目标存在三状态时域演变模型,在现有ITS多帧自动跟踪算法的基础上,重新推导了基于目标存在三状态的目标混合状态更新过程,提出了EITS。仿真实验结果表明,相比现有方法,EITS明显提升了对遮挡目标航迹的维持能力。未来将增加实测数据对所提算法的有效性进行实验验证。
附 录
将目标存在概率P(χk|Zk)展开:

注:χk,0表示门限内没有目标量测被框到,χk,i表示第i个目标量测被框到。
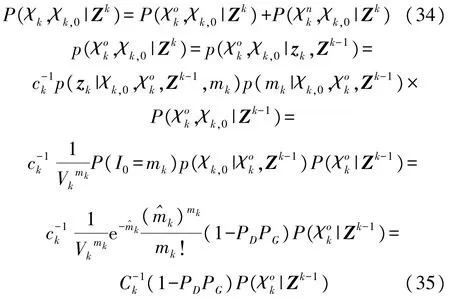
式中:c-k1和Ck-1为预设常数项。
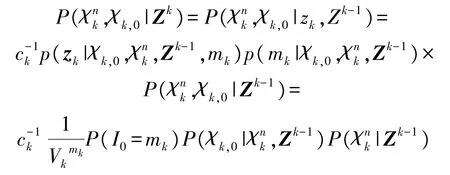
式中:
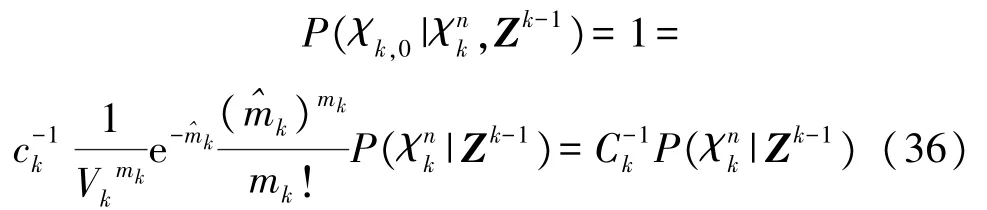
χk,0,χok的假设下,I0=mk表示杂波个数。P(I0,表示杂波个数时间上服从泊松分布。
因此式(34)可表示为:
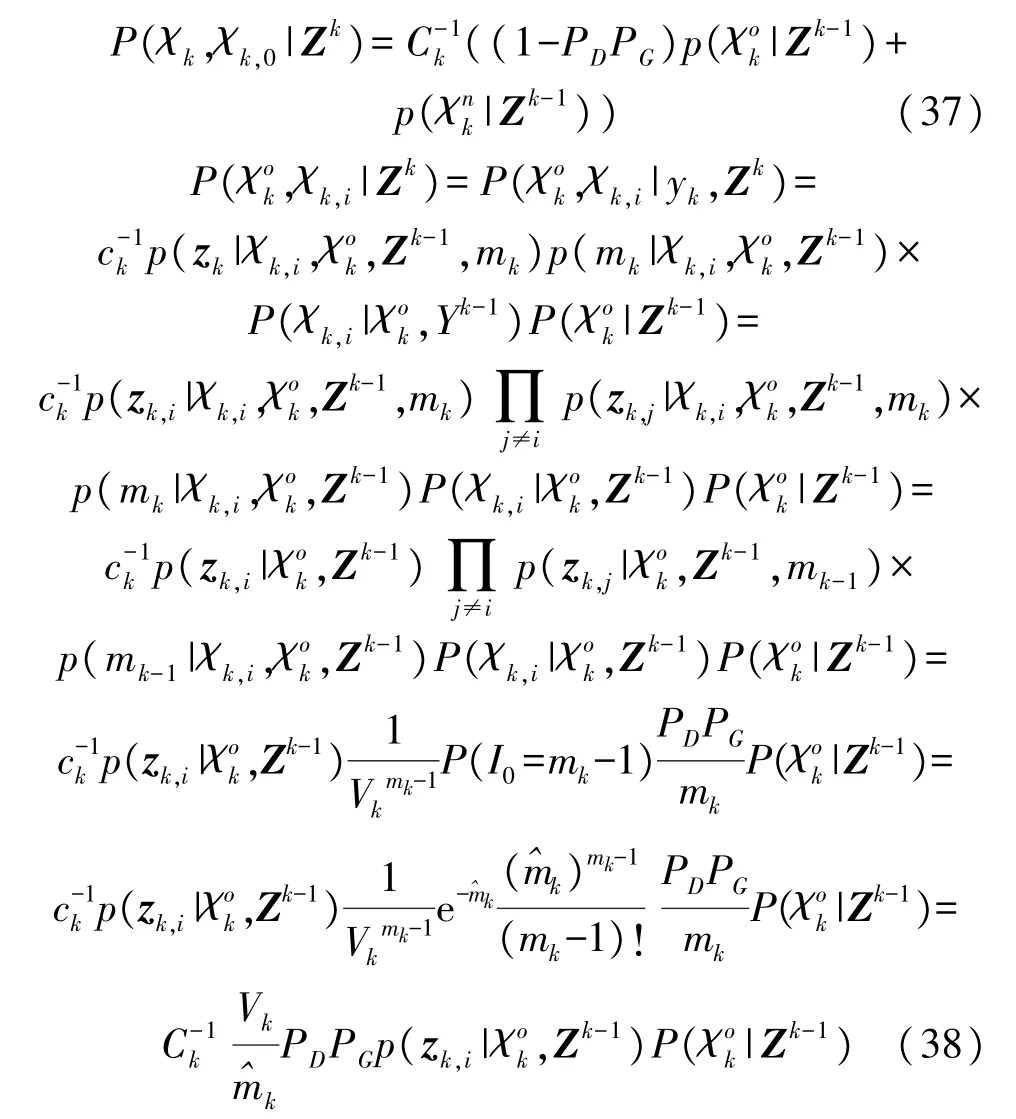
的假设下,I0=mk-1表示杂波个数为mk-1,其中
由概率知识可知:

式中:

将式(38)和式(40)代入式(39)中得到:

将式(36)和式(40)代入式(35)中得到目标存在更新P(χk|Zk)

令Λk=1-δk。


