爆炸地震动下储液结构动力响应试验研究

张浩天， 赵雪川， 宋春明， 吴红晓， 郑际镜， 岳松林， 程怡豪

(1. 陆军工程大学 爆炸冲击防灾减灾国家重点实验室， 南京 210007； 2. 96911部队， 北京 100010)

世界格局与战争形态不断演变，各国争相运用高新技术研发和改进武器装备。在持续紧张的安全形势之下，国防工程建设与防护技术研究面临着严峻的挑战。作为工程防护关注的特种结构之一，储液结构(liquid storage structures ，LSS)在给排水系统和石油化工等方面有着重要的应用，关乎水源、油料等战略资源的储备安全[1-3]。在面临突发武器打击和偶然爆炸袭击，特别是核武器爆炸时，强烈的冲击地震动将导致储液结构产生动力响应，严重时将造成结构的损伤破坏，乃至引发巨大的次生灾害，对人民群众的生命和财产安全造成极大的威胁[4-6]。因此，有必要开展爆炸地震动下储液结构的动力响应研究，对于补充和完善国防工程理论体系，提高工程防护能力具有重要意义。

当前，国内外学者围绕储液结构开展了大量研究工作。其中，储液结构动力特性研究是分析结构动力响应的基础，魏发远等[7-9]将储液容器简化为梁式结构，分别基于悬臂梁弯曲、剪切、弯剪变形理论建立了储液结构的振动方程，并指出工程应用时可根据结构高宽比选用不同变形理论进行近似计算。Kim等[10]对储液结构单一壁板进行分析，建立了固支-自由-对边简支板和固支-自由-对边固支板两种计算模型，发现随着壁板长高比的增大，结构基频逐渐趋近于悬臂梁模型计算结果。Hashemi等[11]提出了储液结构四面壁板的振动分析方法，在水平和竖直方向分别利用连续梁和悬臂梁变形理论，组合得到了储液结构折板振型。杨鸣等[12]基于声固耦合算法分析储液容器固有特性，发现液体的附加质量效应使得结构的固有频率下降，增大了结构在低频荷载下发生强烈振动的可能性。杜永峰等通过数值算例得到类似的结论，指出液动压力使结构自振频率明显下降，同时发现在储液条件下结构振型变化不大，在分析其振动响应时可使用无液结构振型近似替代。程选生等[13]针对Winkler弹性地基和弹性构造底板的情况，推导了储液结构液-固耦合振动方程，讨论了无量纲参数对自振频率的影响。

关于储液结构动力响应，现有研究多以自然地震动作为输入载荷，进行理论推导、数值分析与振动台模型试验。地震激励下需要考虑液体与结构的相互作用问题，以达到科学安全的设计要求。Housner[14]提出了刚性储液结构计算简化模型，将液动压力分为两部分：一是随结构作同步运动的液体产生的脉冲压力；二是结构内液体晃动产生的对流压力，并将液体等效为与结构相连的弹簧-质量系统，在储液结构设计中被广泛应用。Veletsos[15]将储液结构考虑为单自由度体系，并假定结构按照给定形式发生挠曲变形，提出了弹性储液结构简化计算方法，发现考虑结构柔性时液动压力有所增加。Chen等[16]基于广义单自由度理论并考虑悬臂梁变形边界条件进行储液结构动力响应案例分析，发现单自由度方法用于储液结构设计具有较高的精度，同时应考虑高阶模态的影响。Kim等、Hashemi等提出了考虑流固耦合作用和壁板弹性的柔性储液结构动力响应计算模型，在计算脉冲压力时叠加了壁板变形引起的脉冲压力。特别地，针对带有弹性壁板的钢筋混凝土储液结构，程选生等[17]推导了液动压力计算公式。程选生等[18]采用ADINA软件建立储液结构有限元模型，考虑了液体表面重力波的影响，探讨了地震烈度和液位高度对液晃波高和结构壁板变形的影响。张如林等[19]建立流固耦合运动方程并利用ANSYS软件建模，分析了地震波频谱特性对储液结构地震响应的影响，发现当地震波卓越周期接近流固耦联振动周期时，结构响应显著增强。Radnic等[20]利用振动台进行地震激励下储液结构的动力响应试验研究，讨论了激励特性、壁板刚度与储液水位等参数对结构动力响应的影响。程选生等[21-22]采用人工黏弹性边界模拟地基效应进行有限元分析，发现考虑土-结构相互作用后，内部水体液动压力和储液结构动力响应均有较大程度的减小。

综上所述，储液结构在生命线工程中具有重要应用，其安全性备受关注，地震激励下储液结构的动力响应研究已经取得了一些成果。然而，以往研究侧重于自然地震动下储液结构响应，在方法上则偏重于理论计算和模拟仿真。相比之下，爆炸地震动加速度信号具有峰值大、持时短等特点，该震动环境下储液结构动力响应研究较少，特别是在试验方面，由于操作难度大、危险系数高、成本高等，成功案例鲜有，缺少能够指导工程实践的规律性发现，也不足以有效验证和补充相关理论与数值研究结果。因此，本文开展爆炸地震动下储液结构动力响应试验研究，对不同强度地震动下，处于无水、浅水、深水液位状态的储液结构进行振动台试验，同时结合理论方法与相关设计规范，分析结构振动加速度、结构变形、动水压力等动力响应的变化规律，以期为国防工程中储液结构的研究与设计提供有益参考。

1 试验概况

1.1 试验设备

结构试验于爆炸冲击震动模拟平台进行，如图1所示。该平台由陆军工程大学爆炸冲击防灾减灾国家重点实验室研制，用以模拟核武器爆炸冲击震动环境[23]。平台试验时，用挂钩吊住摆锤，卷扬机通电提升摆锤至预定高度后释放，自由下落的摆锤撞击振动台，提供单次近半正弦加速度脉冲，通过调整摆锤下落高度与缓冲垫块厚度，可改变输入加速度波的峰值与脉宽。其中，下落高度定义为摆锤自释放至水平撞击振动台，其锤头重心下降高度，示意图如图2所示。需要说明的是，爆炸震动与爆炸参数、介质条件、结构特性等因素有关，该平台以冲击荷载对爆炸震动环境进行模拟，究其原理：一是反应谱等效[24-25]，将结构系统简化为若干单自由度系统，爆炸震动对结构的作用效果与对各单自由度系统作用效果相同时，可对爆炸震动加速度信号进行反应谱分析，并以半正弦加速度信号反应谱包络，则半正弦加速度脉冲峰值和脉冲持时即为相应爆炸震动加速度等效值；二是波形等效，爆炸地震动的波形难以准确预测，通常采用某一较符合实际情况的假定波形进行参数分析。设计中可近似将自由场地运动参数取为结构运动参数，而半正弦类脉冲及其主导的加速度信号是爆炸试验典型波形之一[26-27]。

图1 爆炸冲击震动模拟平台Fig.1 Explosion shock and vibration simulation platform

图2 摆锤自由下落Fig.2 Free falling of the pendulum bob

1.2 模型结构及传感器布置

试验模型为地面式矩形无顶盖储液结构，其尺寸特征参考地下工程典型储液结构，如图3所示。模型材料为201不锈钢，长1 200 mm，宽900 mm，高750 mm，壁厚10 mm，存储液体为常温常压下的自然常用水。储液结构底板与震动平台对应布置φ30 mm孔洞，通过螺栓连接，结构长边平行于加载方向。动力试验过程中，布置一系列传感器来记录各种参数，如图4所示。其中，加速度传感器(记为A)与动水压力传感器(记为P)沿加载方向布置，分别测量加载后结构的振动响应、结构受到的动水压力，应变片(记为S)沿结构短边方向布置，反映结构的变形情况，以上传感器均为单向式。

图3 矩形储液结构Fig.3 Rectangular LSS

图4 传感器布置 (mm)Fig.4 Sensors layout (mm)

1.3 试验工况

分别进行爆炸地震动下无水、300 mm储水、500 mm储水结构动力响应试验，垫块厚度50 mm，通过调整摆锤下落高度H1～H5，提供5种幅值的输入加速度。其中，H1～H5分别为1 140 mm，1 340 mm，1 540 mm，1 740 mm， 1 940 mm。500 mm储水、摆锤高度H3时得到的典型输入加速度时程曲线，如图5所示。该工况下获得幅值15.8g、持续时间15.5 ms的单次加速度脉冲。可以看出，结构底部A1处与振动台台面A0处采集的加速度时程曲线一致性较好，说明螺栓连接紧实可靠，保证了加载过程中振动台与结构之间无相对滑移，试验的有效性得到验证。

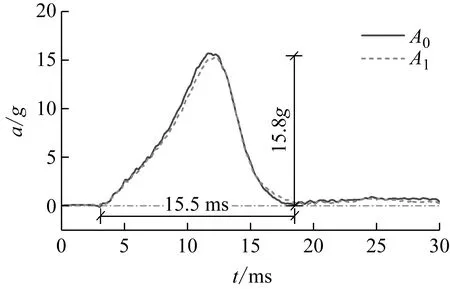
图5 典型输入加速度时程曲线Fig.5 Typical time history curve of input acceleration

对于每种工况进行至少两次平行试验，在试验结果差值小于两者平均值5%的前提下取平均值作为可信数据进行后续分析，否则补充第三次及以上试验直至满足可信条件。不同工况下得到的地震动参数如表1所示，地面峰值加速度(peak ground acceleration,PGA)范围为10.0～26.4g，持续时间(duration time of ground acceleration, TGA)平均值为14.8 ms。经查阅文献资料[28-29]，了解到加速度型地震动强度参数可以较好地表征地震动对结构的潜在破坏作用，同时考虑到GB 50011—2010《建筑抗震设计规范》[30]将峰值加速度作为地震动强度指标，本文亦选取峰值加速度这一参数描述地震动强度特性，以便于分析爆炸地震动对储液结构动力响应的影响。此外，由于篇幅有限，而不同地震动输入条件下动力响应时程曲线变化规律基本一致，仅展示500 mm储水、15.8g地震动强度(摆锤高度H3)时得到的典型时程数据，并分析储液状态、地震动强度对响应峰值等参数的影响。

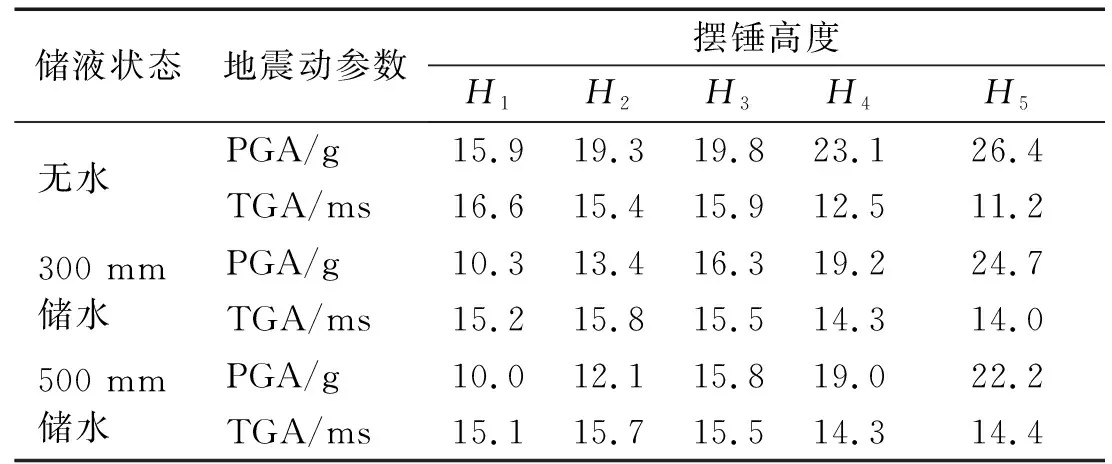
表1 不同工况下地震动参数Tab.1 Seismic load parameters under different working conditions

2 试验结果与分析

2.1 结构动力特性分析

结构的动力特性包括固有频率、阻尼比、振型等，通常认为固有频率对挡墙等短周期结构的地震响应有很大影响[31]。本文振动台模型试验中，通过传递函数分析法确定结构的动力特性参数[32]，传递函数Ha(ω,zj)计算为

(1)

式中：GXX(ω)为振动台台面A0处加速度时程信号的自功率密度函数；GXY(ω,zj)为结构测点Aj(j=2,3,4)处加速度时程与振动台台面A0处加速度时程信号的互功率密度函数。描绘复函数Ha(ω,zj)的幅值-频率曲线，其首个峰值对应的频率fn即为结构固有频率。

不同储液状态下得到的加速度传递函数幅值-频率曲线，如图6所示。由图6可知，结构壁板不同高度测点A2，A3，A4得到的结构固有频率基本一致，取3处测点计算结果的平均值为结构固有频率。相比于无水结构(fn=54.15 Hz)，300 mm储水结构(fn=48.84 Hz)和500 mm储水结构(fn=38.56 Hz)自振频率分别下降9.82%，28.80%，说明储液深度的增加使储液结构固有频率下降，与以往杜永峰等和杨鸣等研究的结论一致。

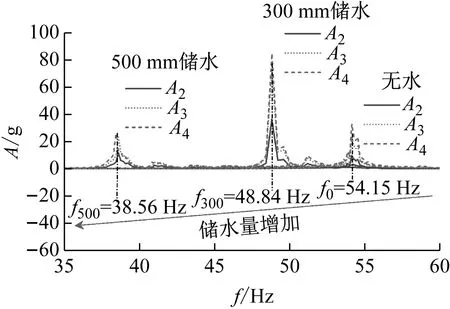
图6 结构加速度传递函数幅值-频率特性曲线Fig.6 Amplitude-frequency characteristic curve of structural acceleration transfer function

2.2 结构振动加速度响应分析

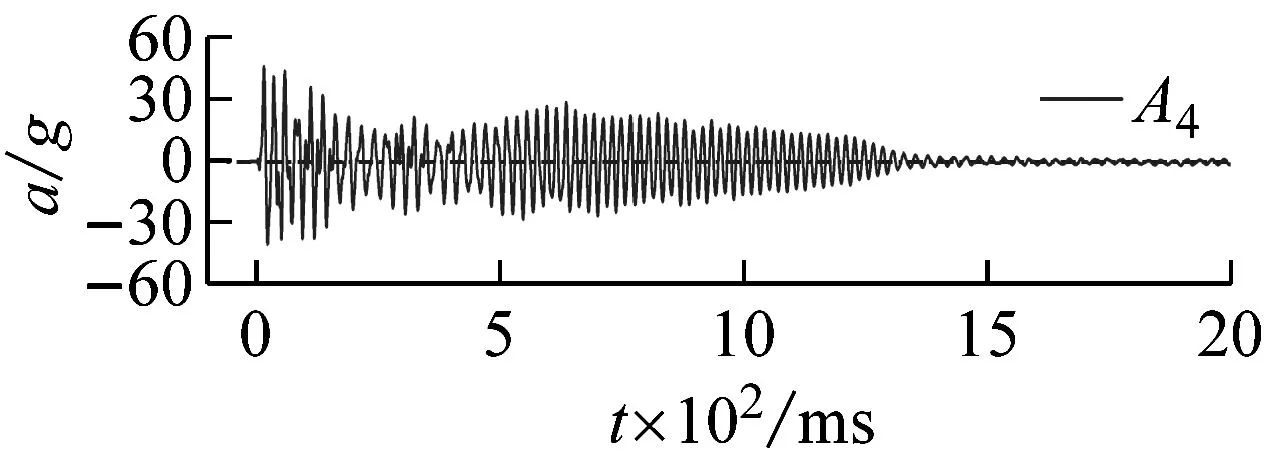
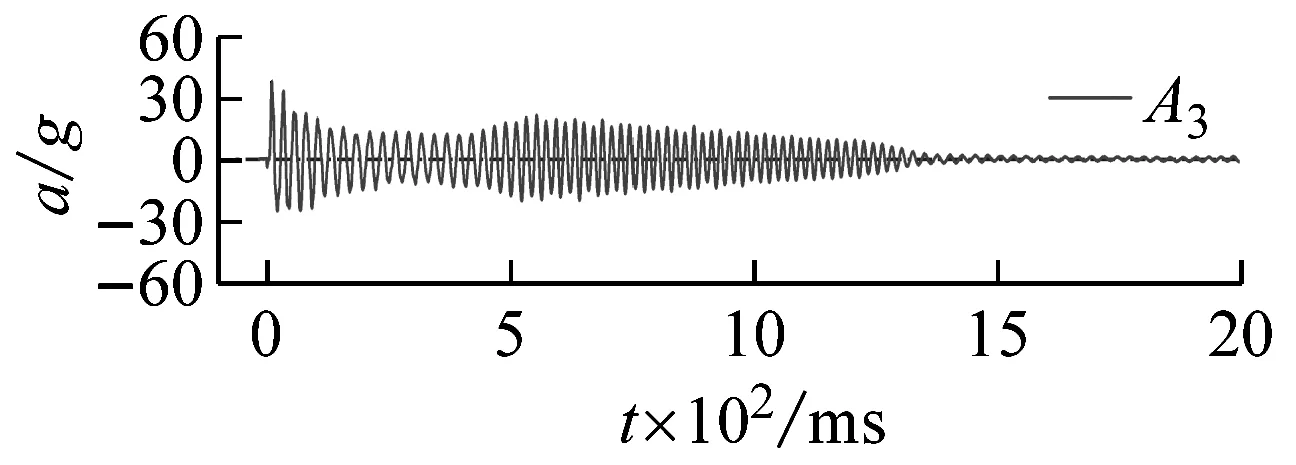
500 mm储水、15.8g加载条件下，测点A2，A3，A4处结构振动加速度响应典型时程曲线，如图7所示。由图7可知，受冲击荷载后结构振动加速度迅速达到峰值，在低阻尼作用下，往复振动幅值逐渐减小。加载后120 ms内输入加速度与不同测点处结构加速度随时间变化的规律，如图8所示。由图8可知，由振动台台面A0测点至顶部A4测点，加速度曲线峰值依次出现，说明地震动影响由底部逐渐传至顶部。为了描述地震动从基础传递到上部结构的变化情况，采用传递系数β表征结构加速度沿模型高度的放大或者衰减效应，β的定义为测点加速度峰值与台面输入加速度峰值的比值，即

(a)

(b)

(c)图7 结构加速度响应典型时程曲线Fig.7 Typical time history curve of structural acceleration response

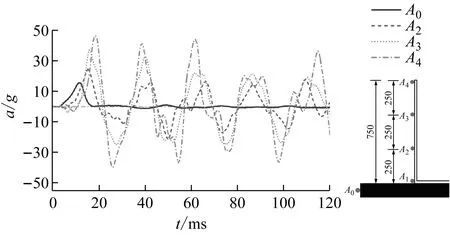
图8 结构加速度响应规律对比Fig.8 The comparison of the law of structural acceleration response

β=ai/a0

(2)

式中：ai为壁板上A2～A4测点加速度峰值；a0为台面A0输入加速度峰值。

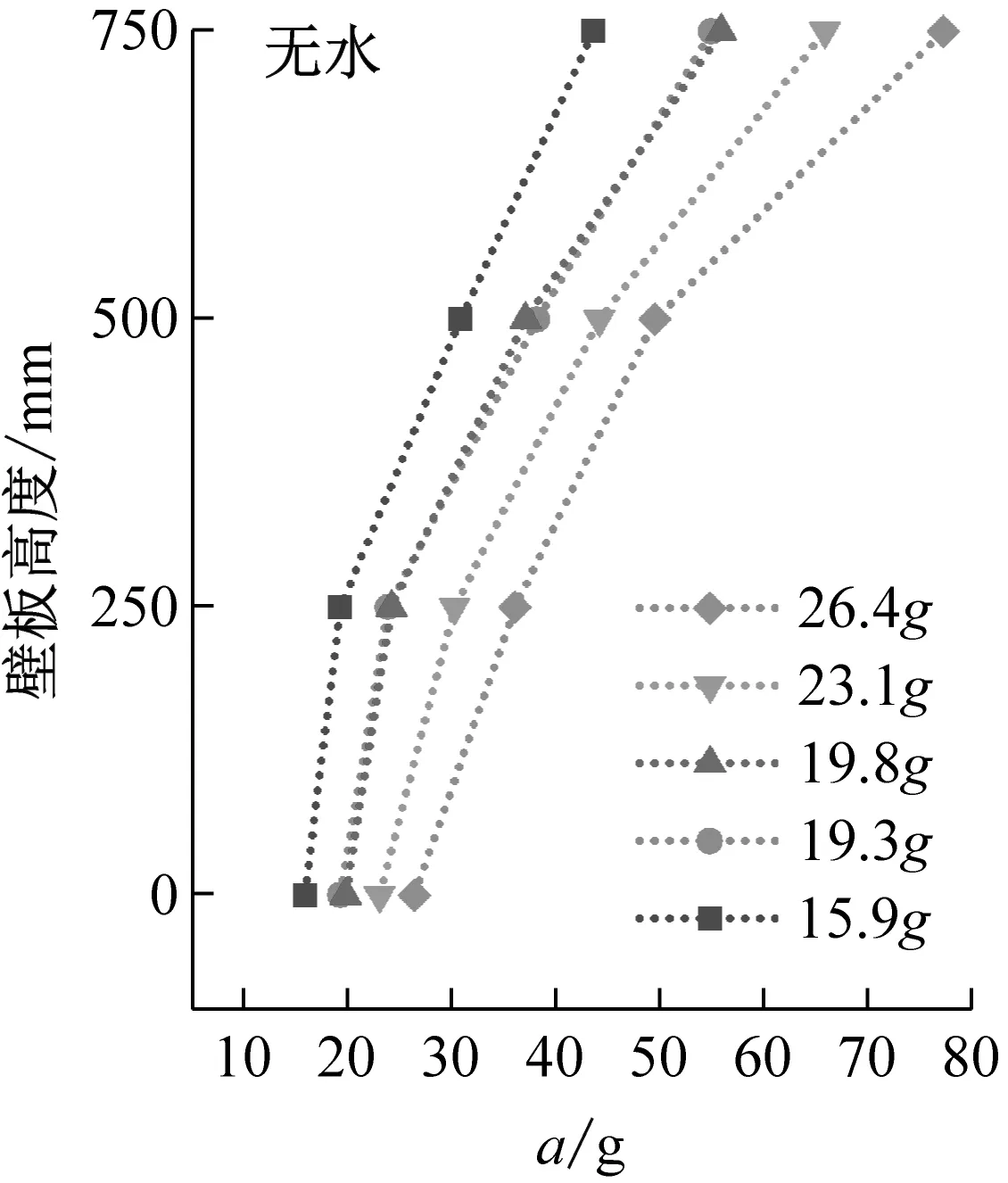
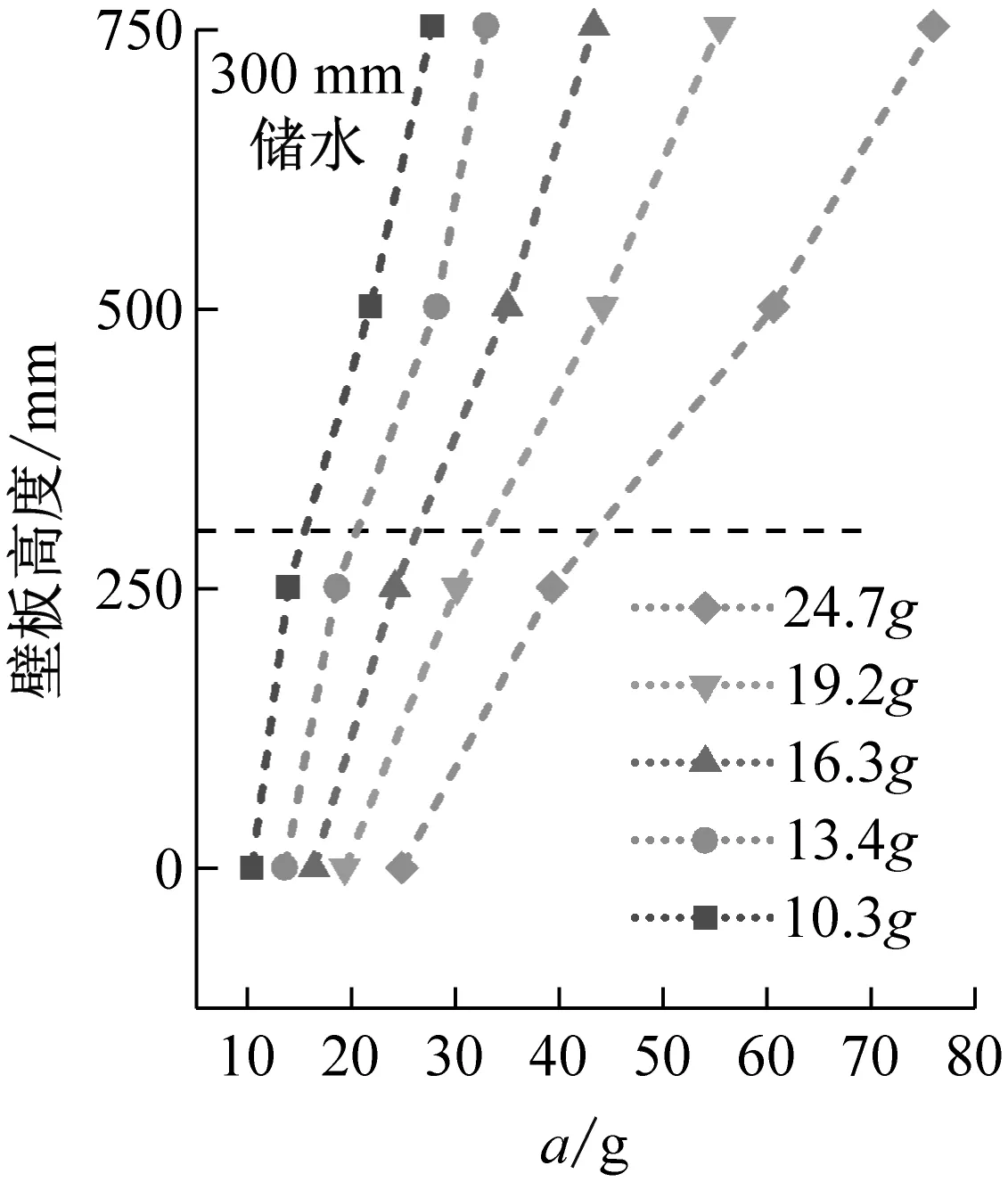
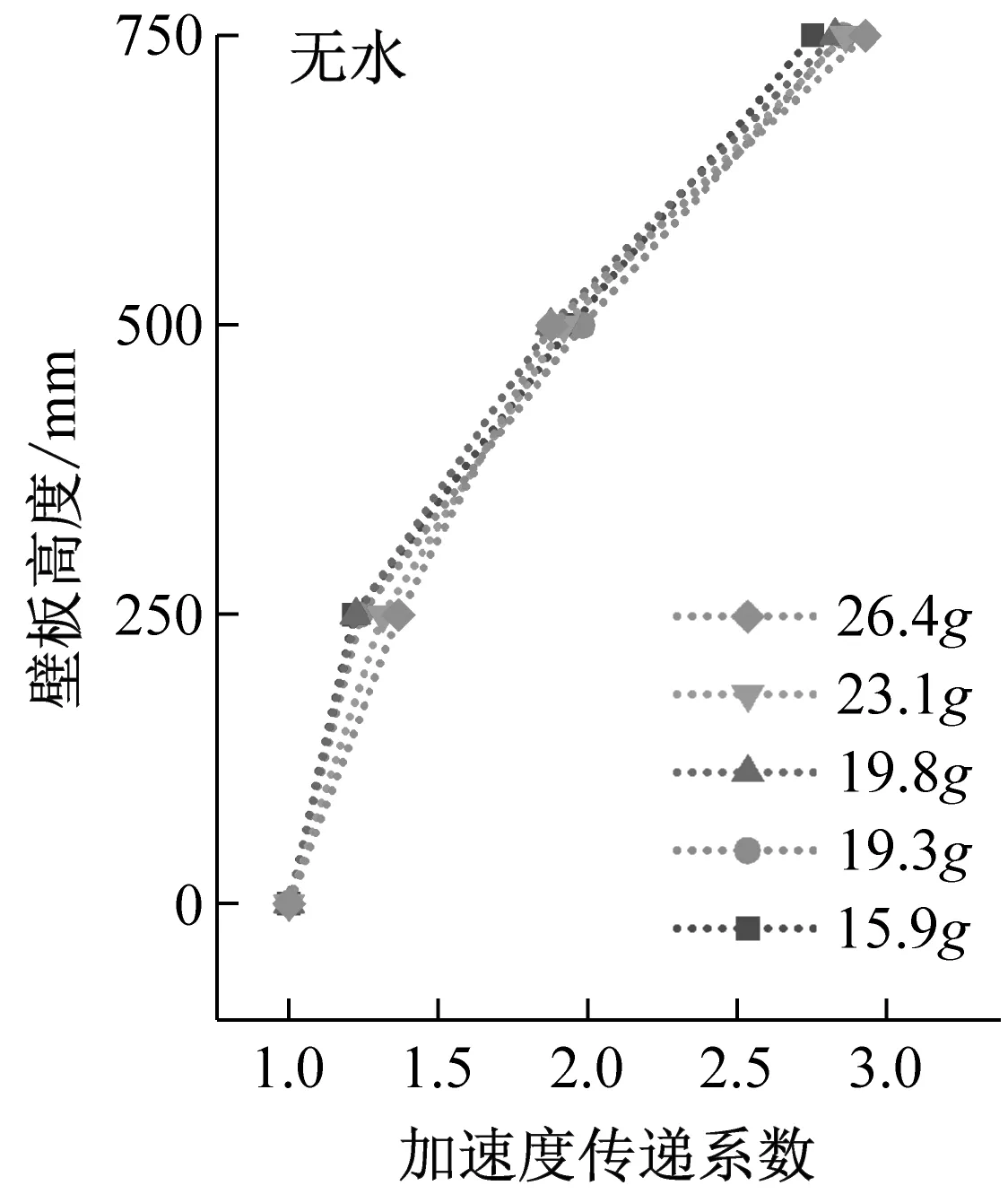
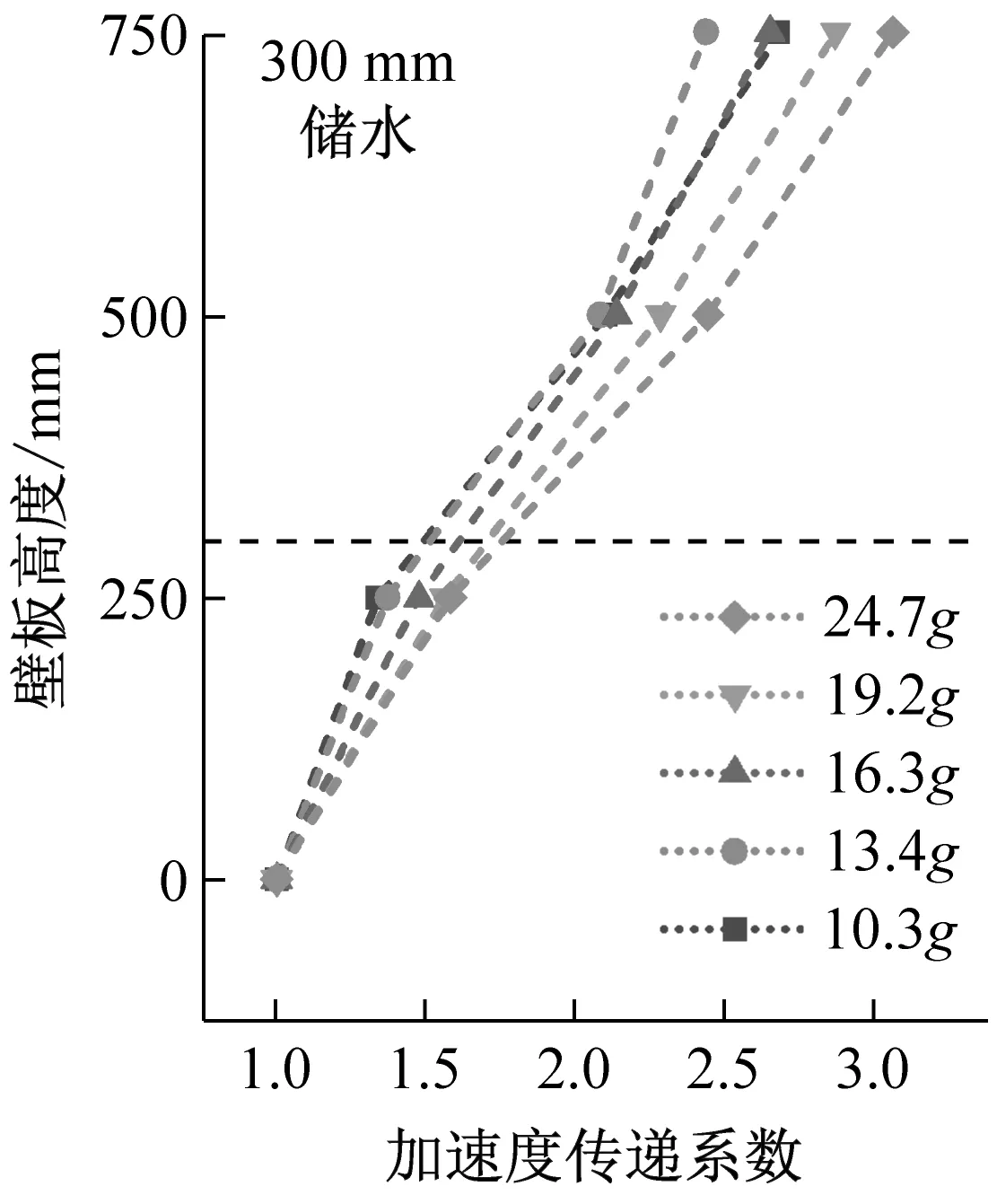
结构加速度峰值与加速度传递系数沿壁板高度变化规律，如图9、图10所示。由图9、图10可知，由壁板底部至顶部，加速度峰值呈现非线性增大趋势，传递系数均大于1，说明地震动在由基础向上部结构传递的过程中存在递增的放大效应，在结构顶部放大效应最为明显。无水条件下，结构加速度传递系数沿结构高度呈加速增大趋势；储水条件下，液面以下由于液体的附加质量效应，结构加速度放大效应更加显著。因此，以储水液面为划分界面，加速度传递系数沿壁板底部至顶部呈现先加速增大、后减速增大的趋势。

(a)

(b)

(c)图9 加速度峰值沿壁板高度变化Fig.9 Peak acceleration varies along the height of the wall

(a)

(b)

(c)图10 结构加速度传递系数沿壁板高度变化Fig.10 Acceleration transfer coefficient varies along the height of the wall

不同工况下，结构加速度传递系数随输入加速度变化曲线，如图11所示。总的来说，不同储水条件下，随着输入加速度的增大，结构振动加速度放大效应均得到一定提高。无水条件下，曲线变化较平缓，说明随着输入加速度的增加，结构加速度传递系数增幅不大；储水条件下，曲线斜率增加，说明结构加速度传递系数受输入加速度的影响增大，地震动强化效应更加明显。为了直观体现储液状态对加速度传递系数的影响，定义16.0g等级输入加速度(无水15.9g、300 mm储水16.3g、500 mm储水15.8g)和19.2g等级输入加速度(无水19.3g、300 mm储水19.2g、500 mm储水19.0g)，该两种等级输入加速度下加速度传递系数随储水状态变化规律，如图12所示。由图12可知，同一强度等级地震动加载条件下，随着储液深度的增加，不同测点的结构振动加速度放大效应均得到增强。

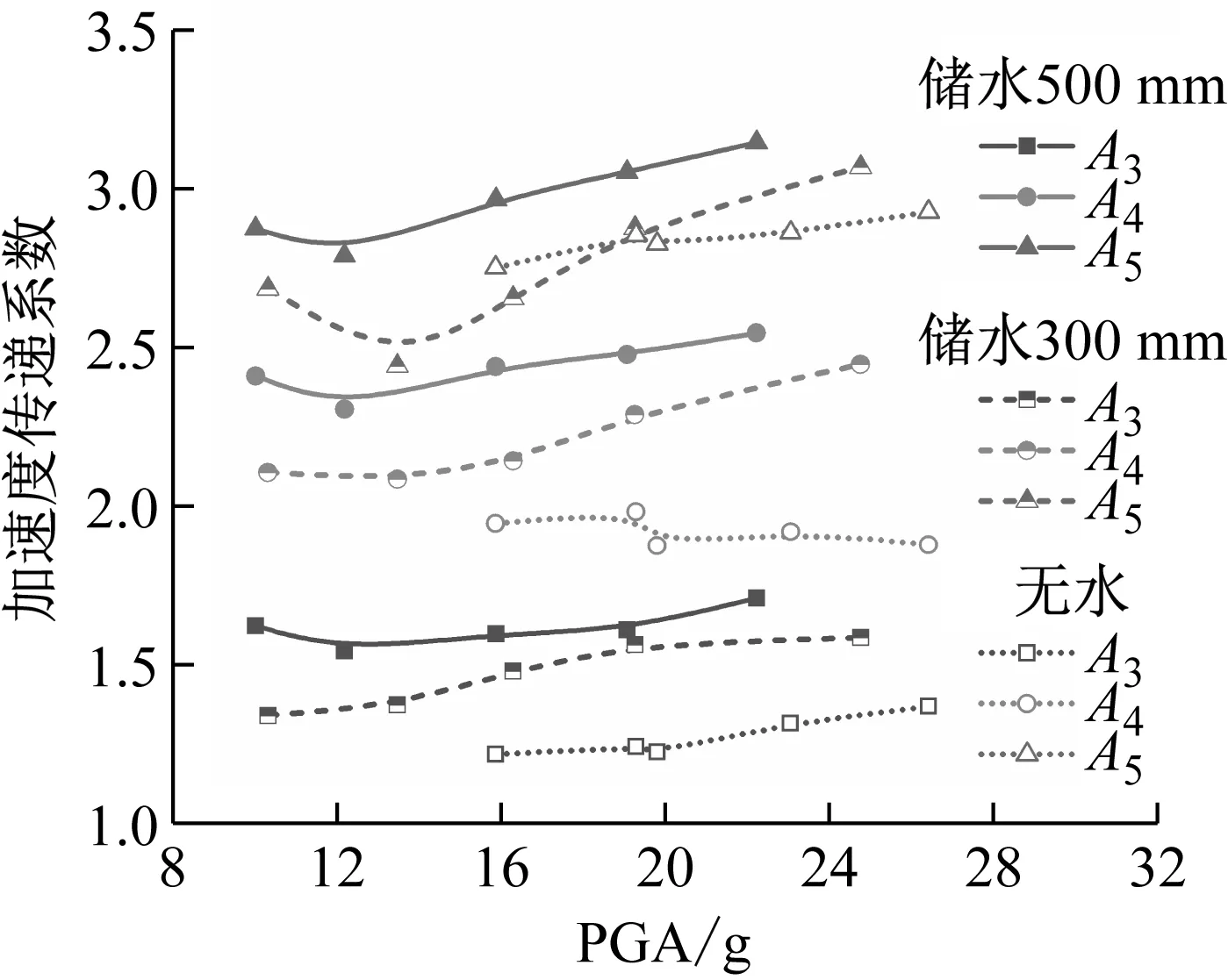
图11 结构加速度传递系数随输入加速度变化Fig.11 Acceleration transfer coefficient varies with the input acceleration

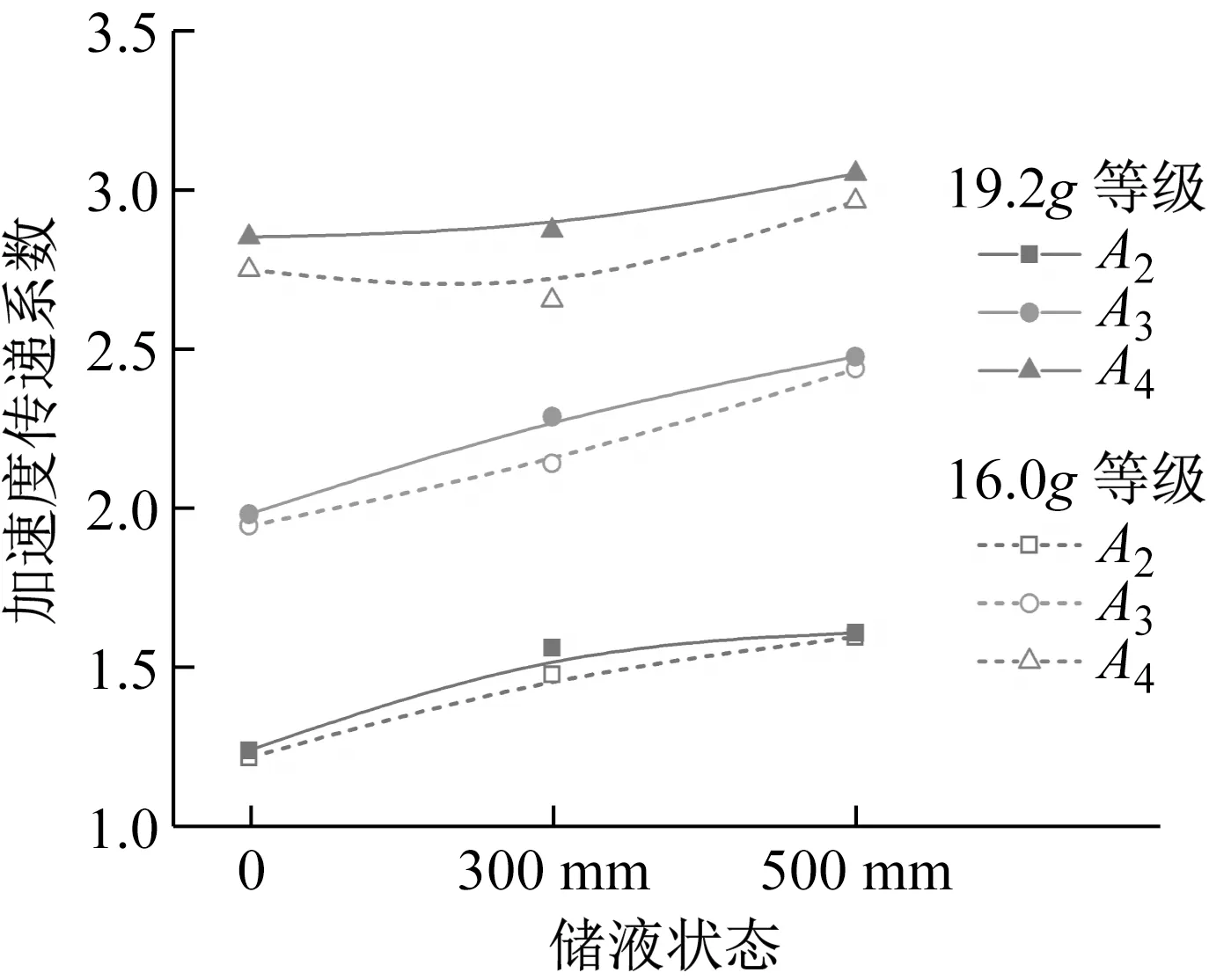
图12 结构加速度传递系数随储液状态变化Fig.12 Acceleration transfer coefficient varies with the liquid storage conditions

2.3 结构应变响应分析

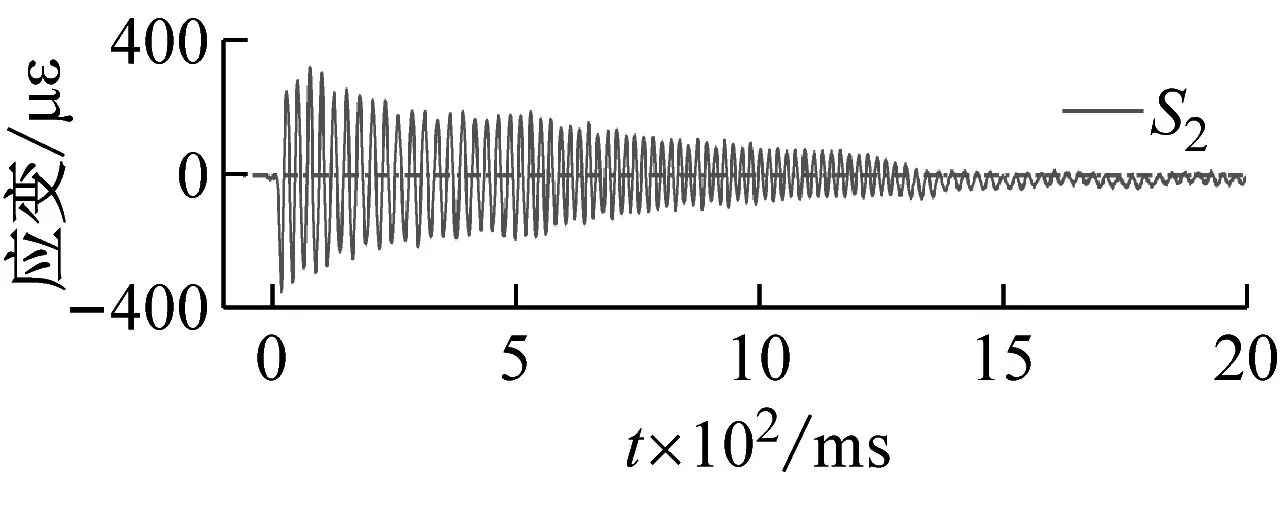
500 mm储水、15.8g加载条件下，测点S1，S2，S3处应变响应时程曲线，如图13所示，可以发现，受冲击荷载后结构迅速达到最大变形，经阻尼消耗能量，往复振动变形幅值逐渐减小。加载后120 ms内不同测点处应力随时间变化的规律，如图14所示，可以看出，不同测点处应变的变化趋势基本一致，由于应变片布置于结构内侧，故加载后应变首先达到负向极值，即结构振动变形首先呈现内侧受压、外侧受拉的状态。

(a)

(b)

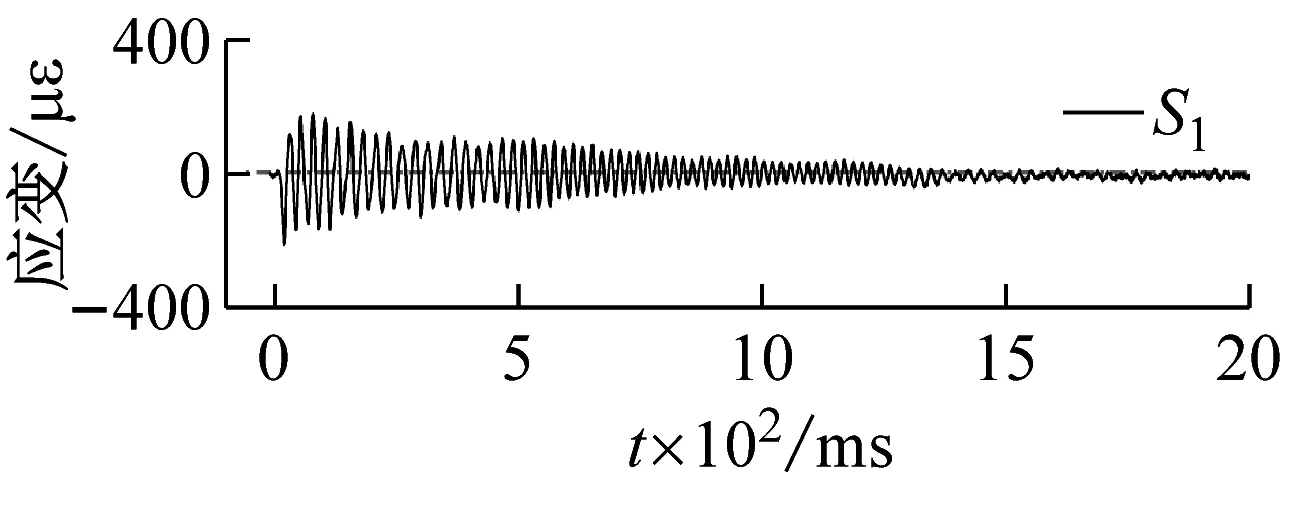
(c)图13 应变响应典型时程曲线Fig.13 Typical time history curve of strain response

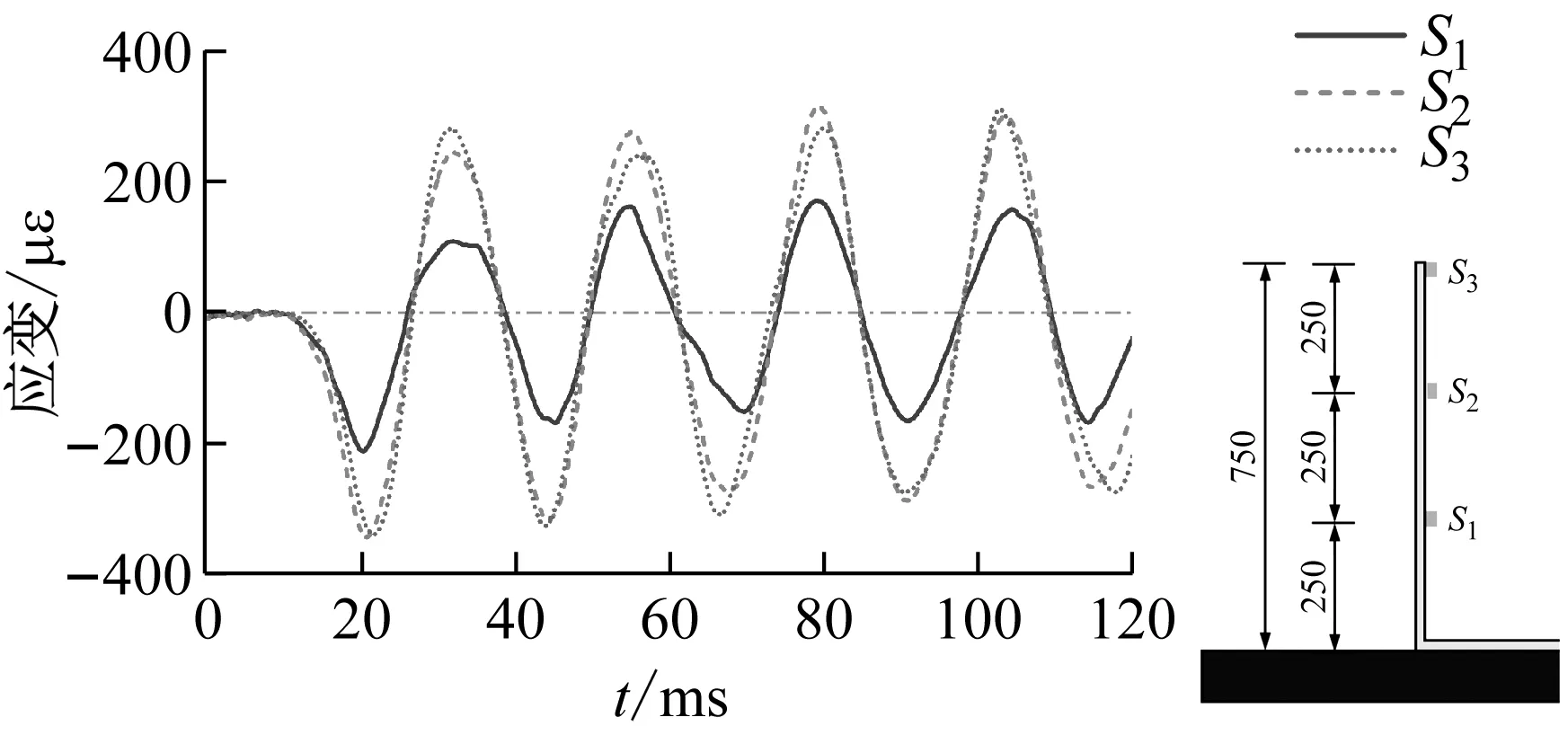
图14 不同测点处应变规律对比Fig.14 The comparison of the law of strain response

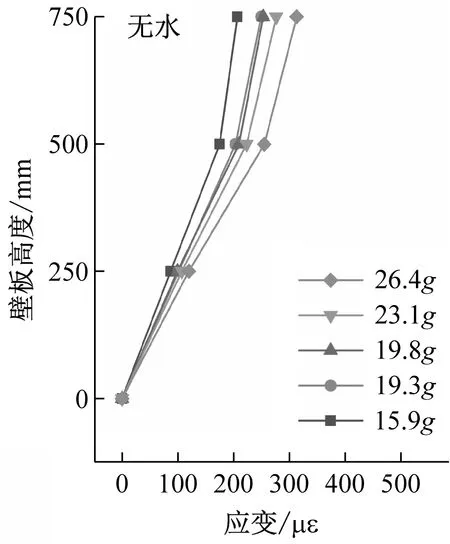
不同储液深度、不同输入加速度下结构应变峰值沿壁板高度变化情况，如图15所示。可以反映出，加载过程中结构动态应力壁板底部至顶部呈现减速增大的趋势，在结构顶部达到最大值。相比于无水结构，储水结构应变分布发生变化，液面以下应变增速提高，液面以上应变增速降低，当储液深度达到500 mm时，结构顶部S3测点处应变与500 mm高度S2测点处应变相差不大。

(a)

(b)

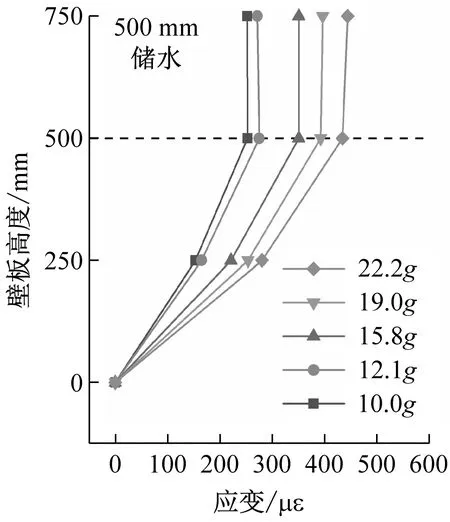
(c)图15 结构应变峰值沿壁板高度变化Fig.15 Peak strain varies along the height of the wall

不同储水条件下，结构应变随输入加速度变化曲线，如图16所示。由图16可知：随着输入加速度的提高，结构应变响应逐渐增大，其中结构顶部增幅更加明显；与无水条件相比，储水条件下曲线斜率增大，说明应变对于地震动强度变化的敏感性提高。16.0g等级和19.2g等级输入加速度下，结构应变随储液状态变化，如图17所示，说明在同一等级地震动加载条件下，储液深度的增加使结构变形值增大。以19.2g输入加速度为例，无水、300 mm储水、500 mm储水条件下结构顶部最大应变值分别提高30.4%，45.9%。

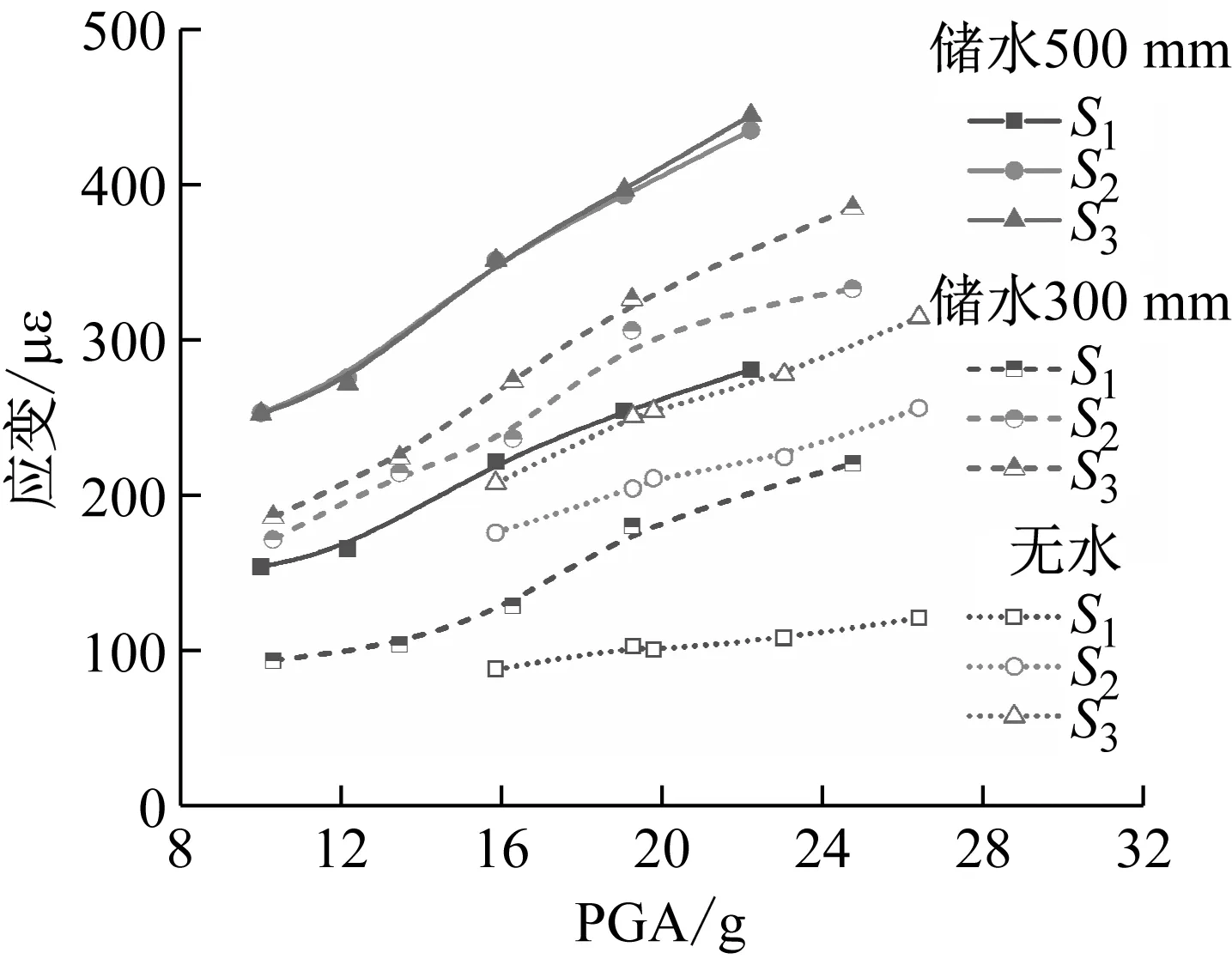
图16 结构应变峰值随输入加速度变化Fig.16 Peak strain varies with the input acceleration

图17 结构应变峰值随储液状态变化Fig.17 Peak strain varies with the liquid storage conditions

2.4 结构动水压力响应分析

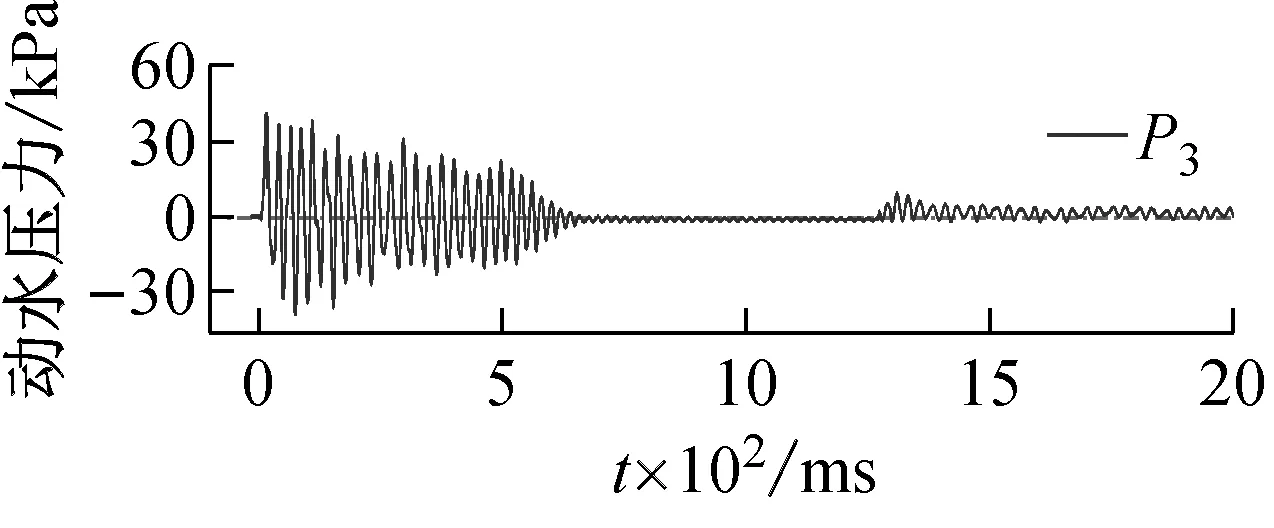
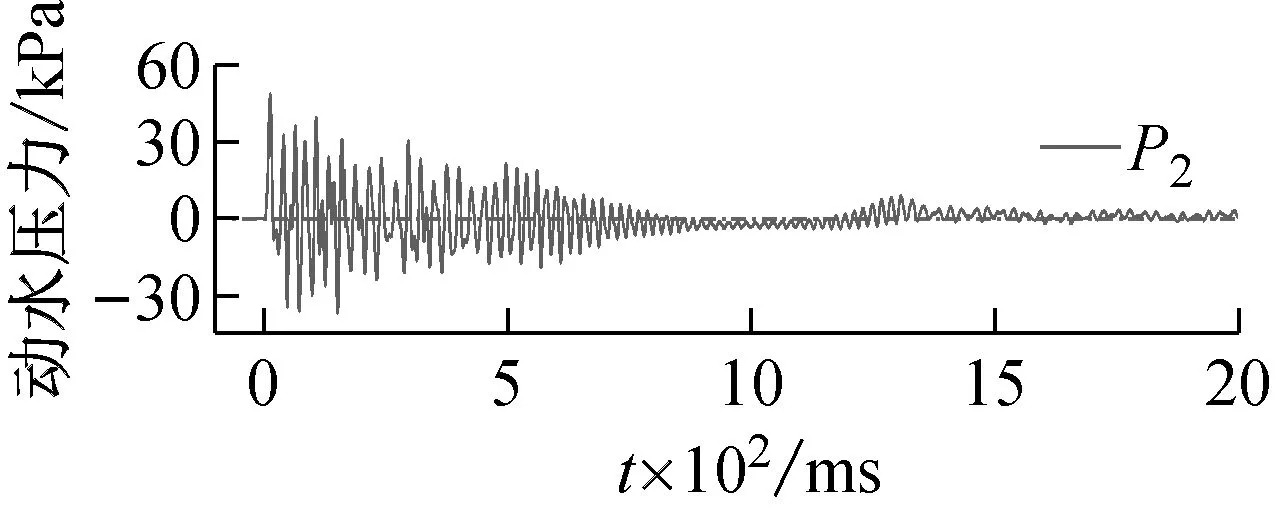
由2.2节、2.3节分析可知，储液状态对于储液结构的动力响应影响很大，动水压力是关键因素。500 mm储水、15.8g加载条件下，测点P1，P2，P3处动水压力响应时程曲线，如图18所示。由图18可知，受冲击荷载后作用于结构壁板的动水压力迅速达到峰值，随着结构振动衰减，动水压力幅值逐渐减小。此外，在800～1 000 ms段，动水压力传感器监测到的响应值为零，这是由于爆炸冲击震动模拟平台缺少限位装置，振动台晃动致结构内储液体流向对侧壁板。加载后120 ms内不同测点处动水压力随时间变化的规律，如图19所示。由图19可知，由结构底部P1测点至上部P3测点，动水压力首个峰值依次出现，说明动水压力响应自结构底部向顶部传递的过程中产生了相位差。

(a)

(b)

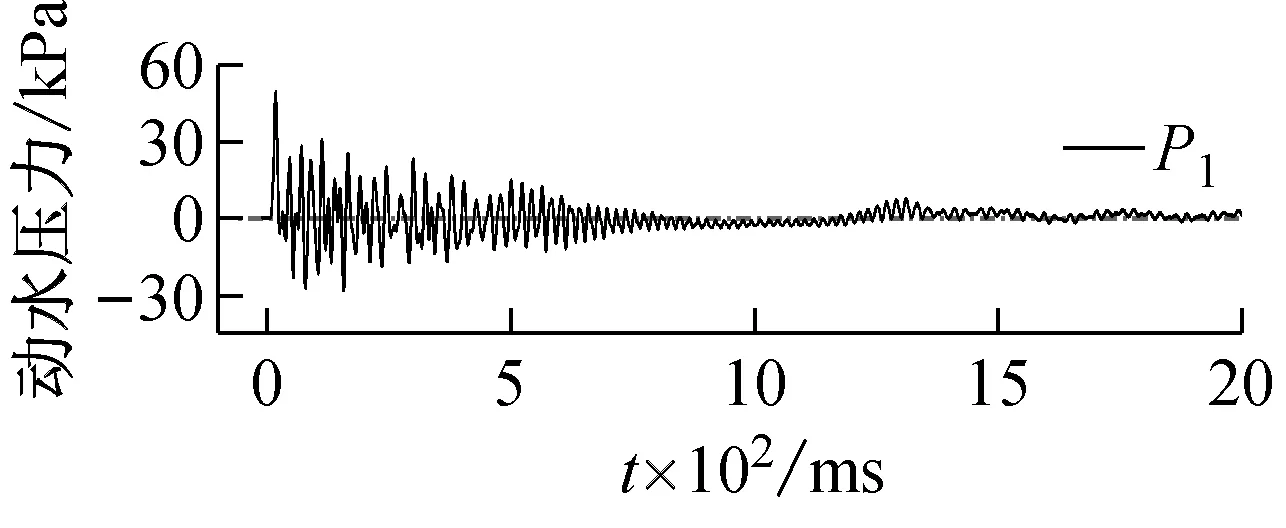
(c)图18 动水压力响应典型时程曲线Fig.18 Typical time history curve of hydrodynamic pressure

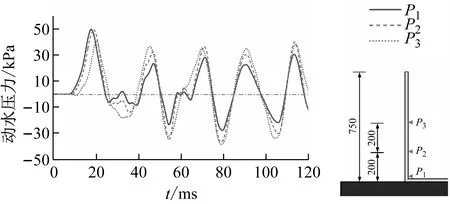
图19 不同测点处动水压力规律对比Fig.19 The comparison of the law of hydrodynamic pressure

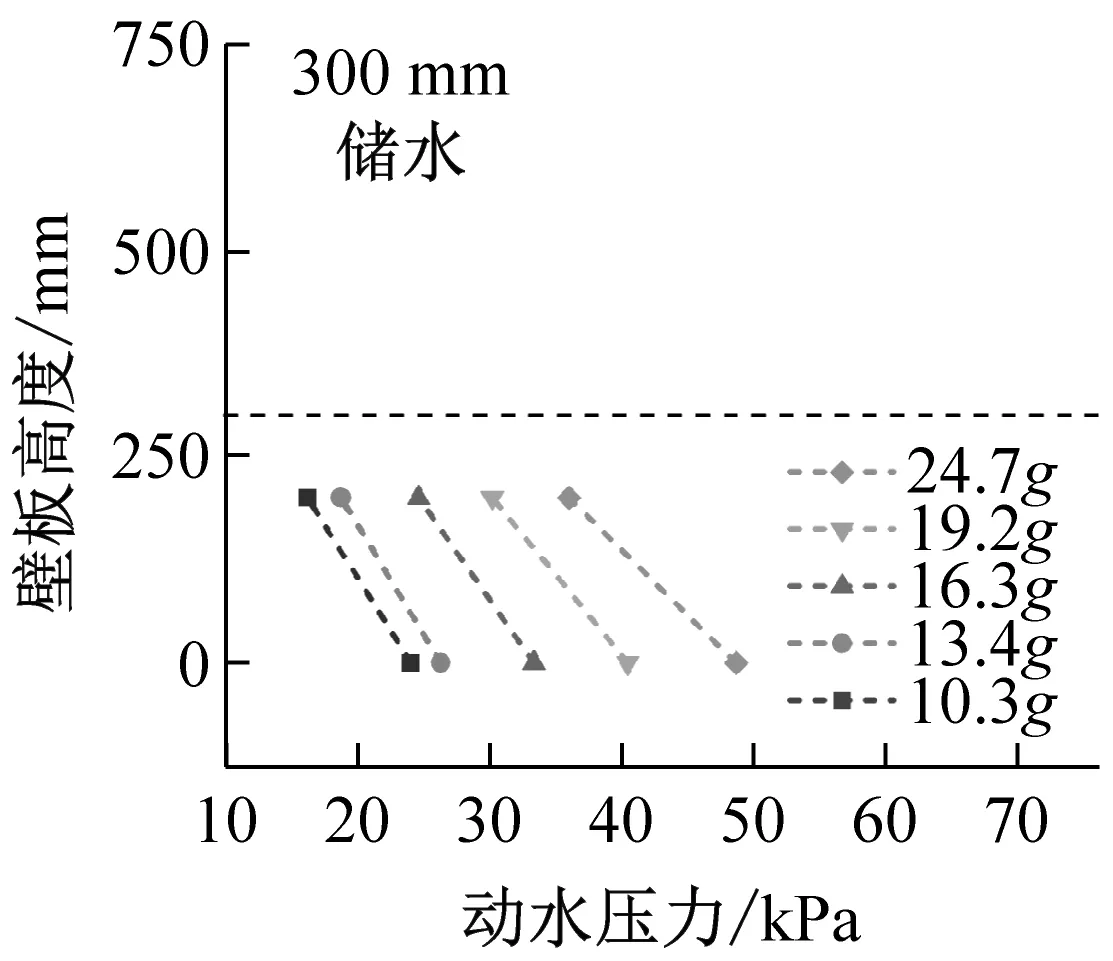
不同储液深度、不同输入加速度下结构动水压力峰值沿壁板高度变化情况，如图20所示。由图20可知，在500 mm储水条件下，动水压力随水深增加表现出减速增大的趋势，结构底部动水压力最大，而2/5水位处与结构底部动水压力相差不大，结构临水部分中下段承受了水平相当且幅值较高的动水压力。

(a)

(b)图20 结构动水压力沿壁板高度变化Fig.20 Hydrodynamic pressure varies along the height of the wall

不同工况下，结构动水压力随输入加速度变化曲线，如图21所示。由图21可知：随着输入加速度的增加，结构承受的动水压力逐渐增大；结构储水由300 mm增至500 mm，在不同加速度加载的条件下，动水压力均有明显的增幅。

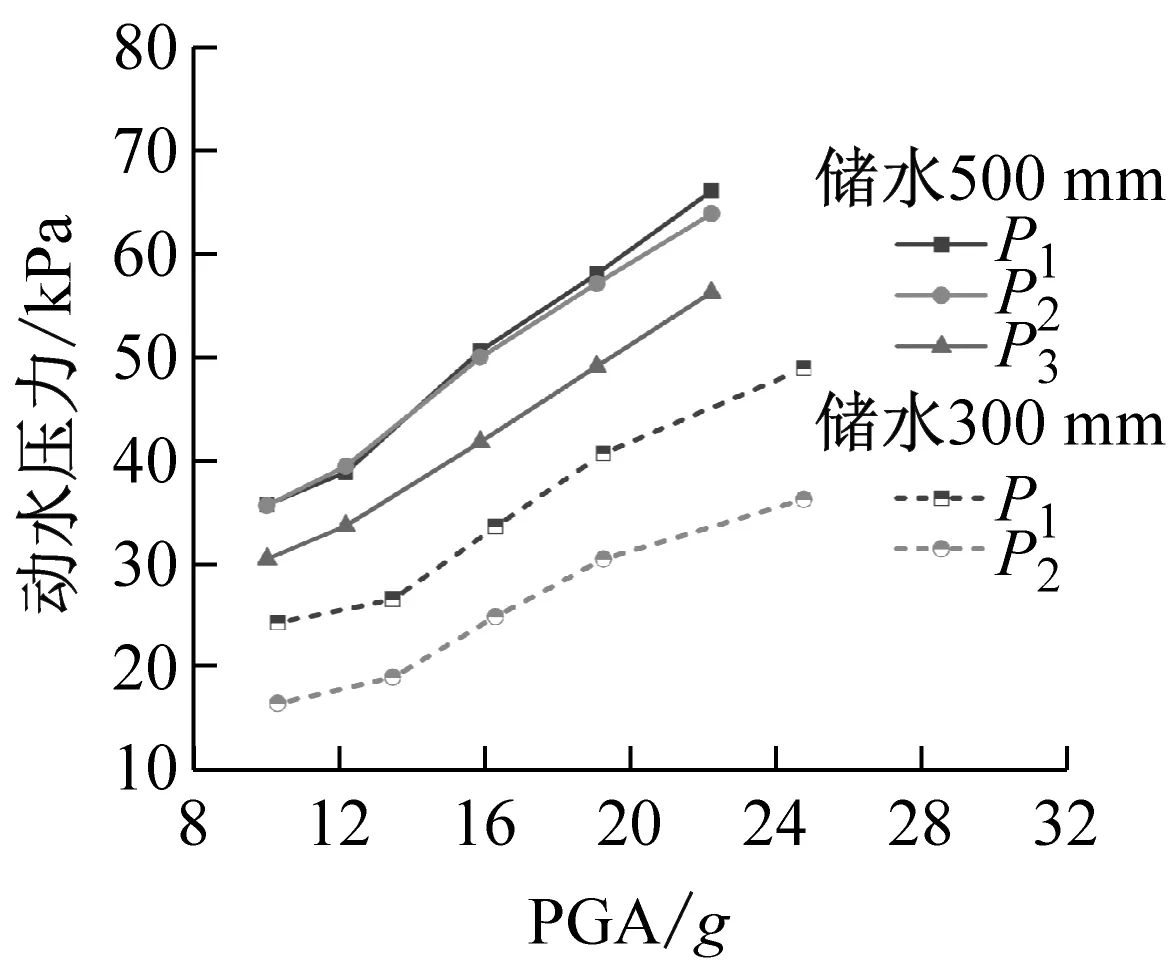
图21 结构动水压力随输入加速度变化Fig.21 Hydrodynamic pressure varies with the input acceleration

3 理论分析与讨论

3.1 储液结构壁板振型探讨

由引言部分可知，以往学者对于储液结构自振特性开展了相关研究，关于壁板振型尚未得到一致结论。本文基于试验数据，对于储液结构壁板振型进行初步的探讨。储液结构计算模型示意图如图22所示，图22中：地震动沿x方向；Lx为矩形储液结构沿地震作用方向的边长；Ly为结构垂直地震作用方向的边长；Hs为结构高度；Hw为储液深度。

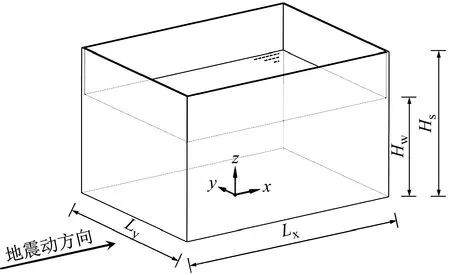
图22 储液结构计算模型示意图Fig.22 Schematic diagram of LSS calculation model

由板壳振动理论[33]可知，矩形板固有振动分析可采用双向梁函数组合级数逼近方法，一般性矩形薄板的挠度振型W(y,z)可表示为

(3)

式中：Ym(y)与Zn(z)分别为与壁板水平y方向，竖直z方向两端边界条件对应的第m与n阶梁振型函数；Amn为待定系数，用于调整梁函数的组合以逼近矩形板振型真实解。矩形薄板的振动方程w(y,z,t)可表示为

w(y,z,t)=W(y,z)T(t)

(4)

式中，T(t)为时间相关的动力函数。因此，得到板内横向应变分量εy为

(5)

将式(3)、式(4)代入可得

(6)

式中，t为壁板厚度。考虑到试验中单向应变片沿壁板水平y方向布置，且均粘贴处于壁板中轴位置(y=0)，故由式(6)可知S1，S2，S3测点应变值对比结果为

εy(S3):εy(S2):εy(S1)=Zn(S3):Zn(S2):Zn(S1)

(7)

该结果反映了结构壁板竖向振型。因此，将图15应变测量结果进行归一化处理，结果如图23所示。

图23 结构应变峰值沿壁板高度变化归一化结果Fig.23 Normalized results of peak strain along the height of wall

图23中除归一化的试验数据外，标注了弯曲悬臂梁一阶振型曲线与剪切悬臂梁一阶振型曲线。可以看出，不同工况下试验值与剪切悬臂梁振型曲线更接近，说明储液结构壁板振动竖向振型更加符合剪切型变形理论。由无水至300 mm储水、500 mm储水，液体附加质量效应出现并逐渐增强，壁板振型在剪切悬臂变形的基础上发生局部变化，表现为液面以下壁板临水部分变形得到增强，上部无水部分变形相对弱化。

3.2 动水压力理论计算与规范对比

考虑到动水压力对于储液结构动力响应的重要影响，抗震设计时需对爆炸地震动下的动水压力进行验算。首先进行理论方法求解，计算模型参考图22。基于程选生等推导的动水压力计算方法，在考虑储液结构弹性变形的条件下，壁板受到的脉冲动水压力pi由两部分组成：刚体运动产生的脉冲压力pg与考虑壁板侧向变形产生的脉冲压力pf，可按式(8)～式(11)计算

(8)

(9)

(10)

(11)

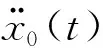
(12)

式中，βmax为单质点弹性结构的最大水平加速度与地震动最大加速度的统计平均值的比值[34]，即

(13)

对于钢筋混凝土储液结构取值2.25。对于本文不锈钢储液结构，以2.2节加速度传递系数统计平均值进行修正，取为2.85。

此外，基于Hashemi等提出的流固耦合理论方法，壁板对流压力pc可按式(14)～式(19)计算

(14)

(15)

(16)

λj=(2j+1)π/2

(17)

αj=λj/Lx

(18)

(19)

以500 mm储水、摆锤高度H3工况为例，通过Maple软件进行理论计算前，以Asym2Sig模型[见式(20)]对地震动加速度信号进行单峰值拟合，结果如图24所示，拟合曲线与试验曲线吻合较好。

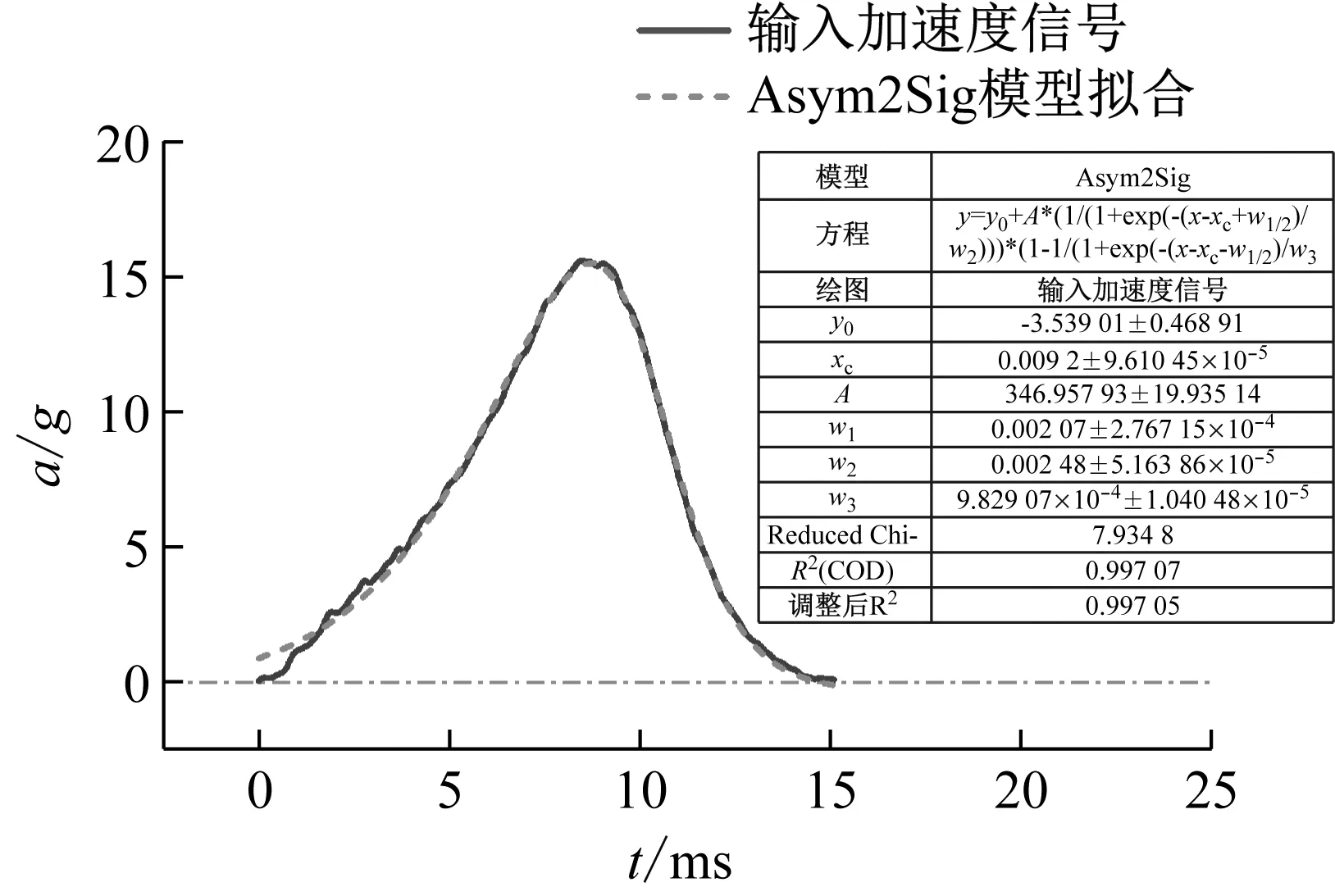
图24 典型输入加速度信号与Asym2Sig模型拟合结果Fig.24 The typical input acceleration signal and the fitting results using Asym2Sig model

(20)

将拟合函数代入式(8)～式(19)，计算得到该工况下动水压力理论值，计算结果如图25～图26所示。图25中呈现了地震动加速度峰值时刻脉冲压力pi、刚体运动脉冲压力pg、壁板变形脉冲压力pf、以及对流压力pc沿临水壁板分布情况。可以看出：液面以下随着水深增加，pi，pf先增大后减小；pg逐渐增大，在结构底部达到最大值；pc逐渐减小，最大值出现在液面处。相比之下，液体晃动产生的对流压力不足脉冲压力的1%，对动水压力影响可忽略。脉冲压力则是动水压力主要组成部分，对储液结构动力响应起主要作用。

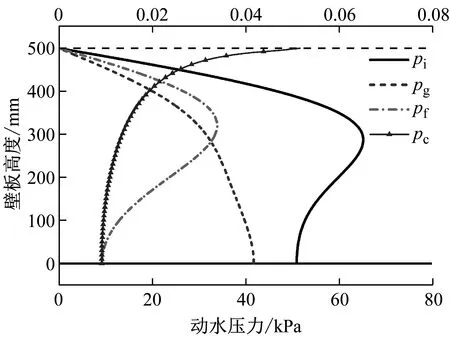
注：脉冲压力pi,pf，pg参照下轴；对流压力pc参照上轴。图25 理论计算动水压力沿壁板分布Fig.25 Theoretically calculated hydrodynamic pressure distribution along the wall

(a) 300 mm储水

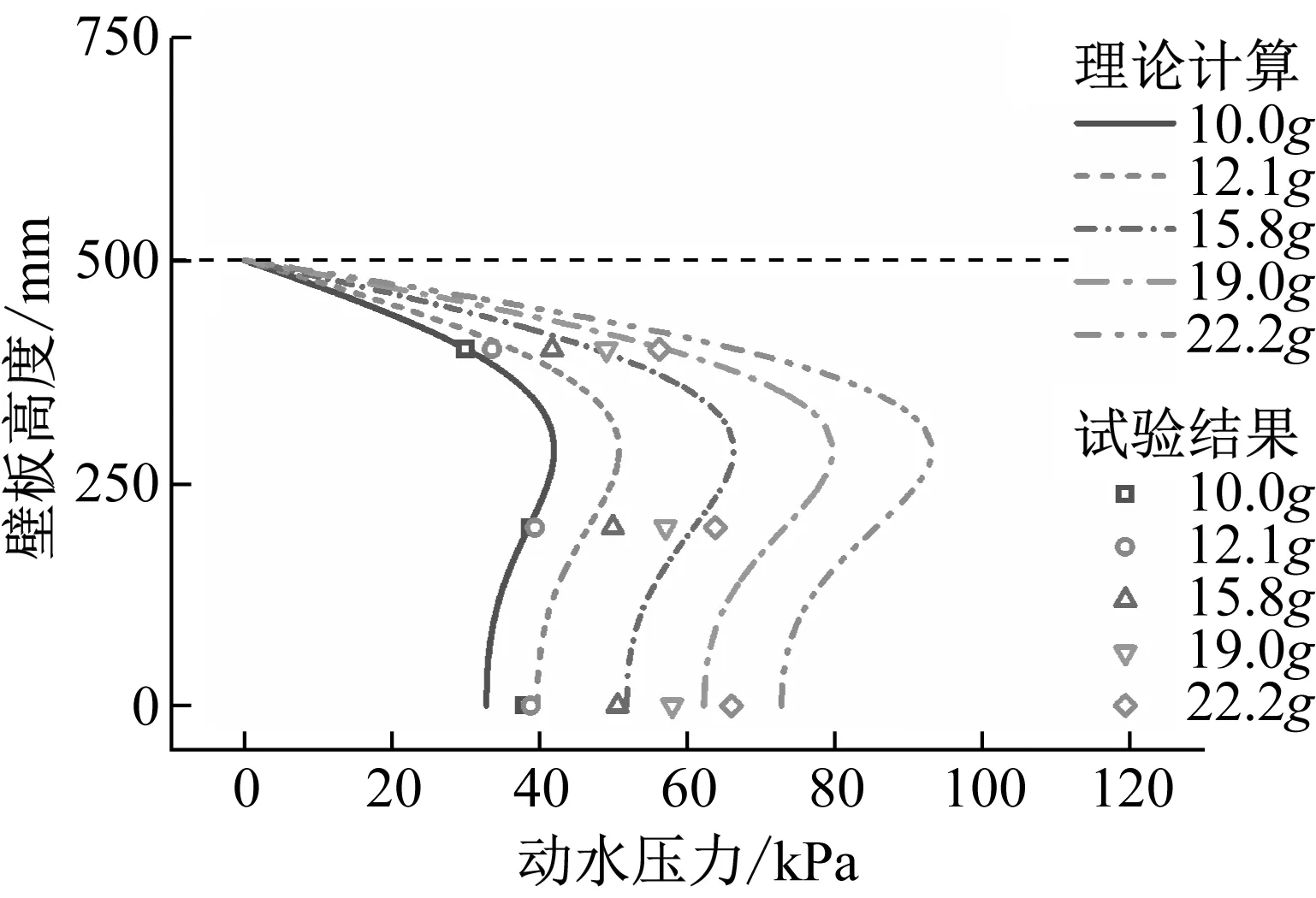
(b) 500 mm储水图26 动水压力理论计算与试验结果对比Fig.26 Comparisons between theoretical calculations and experimental results of hydrodynamic pressure

对比不同测点处动水压力最大值理论计算与试验结果，如图26所示。可以发现两者存在一定偏差，分析其原因，一是式(8)～式(11)计算pg与pf时对结构振型进行简化，弱化了结构响应的非线性；二是式(12)计算pi时作了简化处理，以便于工程设计。但总的来说，理论计算值在结构底部P1，上部P3处吻合较好，不同测点处计算偏于保守，有利于结构安全设计。加之工程设计往往关注计算求解的便利性，上述理论计算方法仍具有较好的适用性，下面结合现有设计规范进行讨论。

现行规范中提供了盛水构筑物动水压力的抗震验算方法。其中，GB 50032—2003《室外给水排水和燃气热力工程抗震设计规范》[35]在进行矩形水池抗震验算时，将壁板受到的动水压力简化为沿平面、沿高度等值分布，并给出地面式矩形水池在水平地震作用下动水压力标准值Fwr,c的计算方法

Fwr,c=KH·γw·Hw·fwr

(21)

式中：KH为水平地震加速度与重力加速度的比值；γw为池水重力密度；fwr为地面式矩形水池动水压力系数，可按表2采用。

表2 地面式水池动水压力系数fwrTab.2 Hydrodynamic pressure coefficient of above-ground pool, fwr

参照规范计算式(21)对动水压力理论计算式(12)进行改进，得到

Fwr,c2=KH·γw·Hw·fwr2

(22)

(23)

将式(23)进一步化简，得到

(24)

式(24)表达了fwr2与Lx/Hw的函数关系，对应函数曲线如图27所示。可以看出，对于本文地面式不锈钢矩形储液结构，GB 50032—2003《室外给水排水和燃气热力工程抗震设计规范》系数fwr偏差较大且不利，需要进行修正。参考规范中常见做法进行离散化处理，得到修正后的动水压力系数fwr2取值表，见表3，可供相关工程按照线性差值法使用。

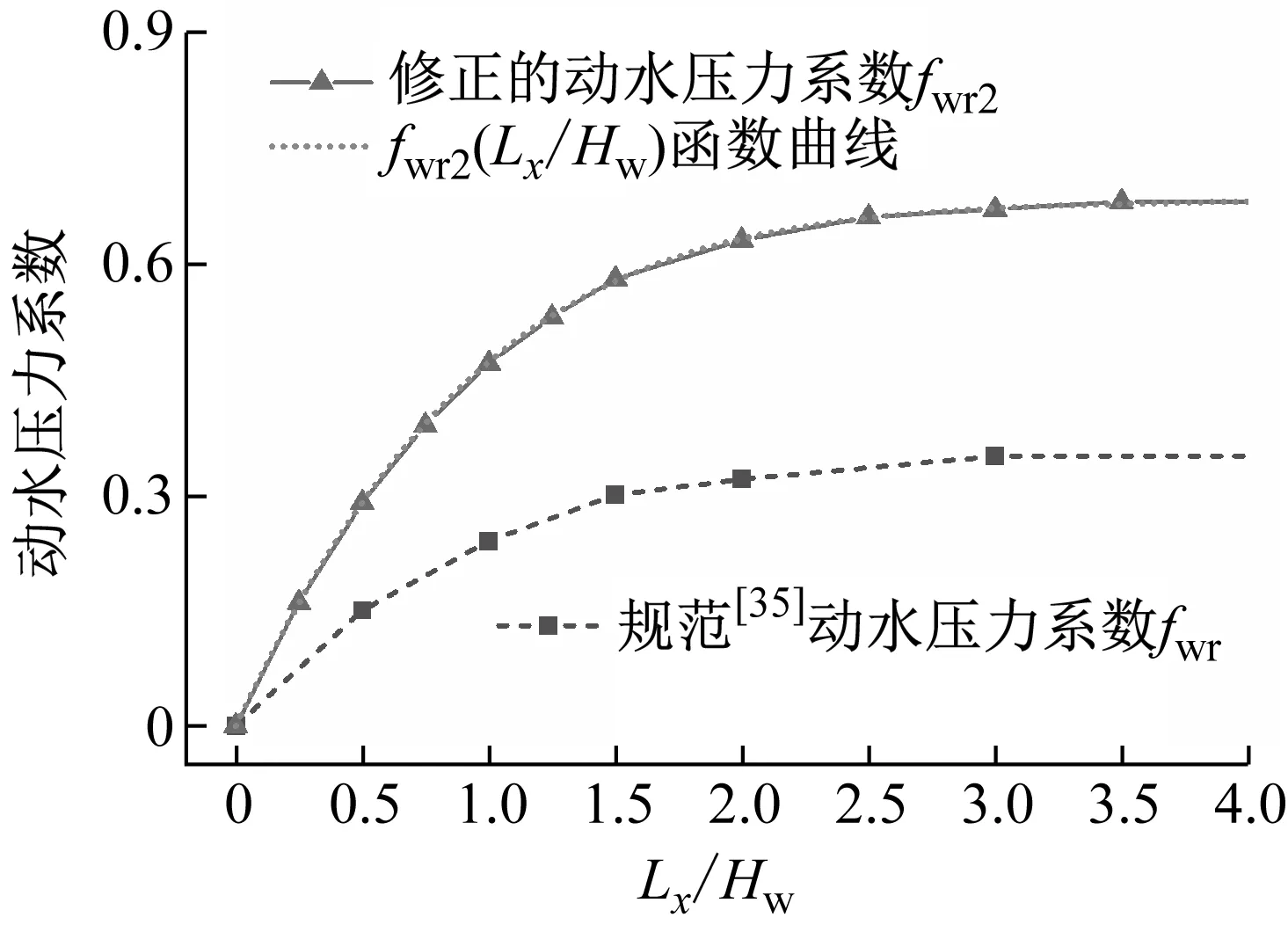
图27 动水压力系数修正结果Fig.27 Modified result of hydrodynamic pressure coefficient

表3 修正后的地面式不锈钢储液结构动水压力系数fwr2Tab.3 Modified hydrodynamic pressure coefficient for ground-mounted stainless steel rectangular LSS, fwr2

此外，在进行储液结构抗震设计时，需要考虑动水压力所产生的倾覆力矩。在推导动水压力计算式的基础上，作用于储液结构壁板上的动水压力所导致的倾覆力矩可计算为

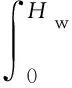
(25)

联立式(12)并参照规范计算式(21)进行改进，得到

(26)

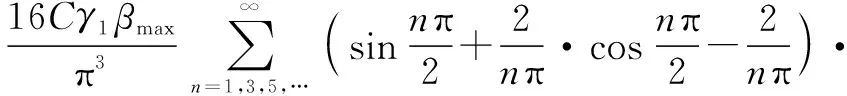
(27)

式(27)表达了倾覆力矩系数mover与Lx/Hw的函数关系，对应函数曲线如图28所示，经离散化处理得到的动水压力倾覆力矩系数mover取值表，见表4，可供相关工程按照线性差值法使用。

图28 动水压力倾覆力矩系数计算结果Fig.28 Calculation result of overturning moment coefficient

表4 地面式不锈钢储液结构倾覆力矩系数moverTab.4 Overturning moment coefficient for ground-mounted stainless steel rectangular LSS, mover

4 结 论

本文利用爆炸冲击震动模拟平台对固有频率为54.15 Hz的地面式矩形无顶盖储液结构开展了动力响应试验研究，得到了峰值加速度范围为10.0～26.4g、平均持时为14.8 ms的地震动荷载，分析了储液状态、地震动强度对储液结构动力响应的影响，结合试验与理论方法揭示了储液结构振型特点和动水压力变化规律，主要结论有：

(1) 通过分析传递函数得到不同储液状态下储液结构的固有频率，发现储液状态影响液-固体系固有频率，由无水到300 mm储水、500 mm储水状态，液-固体系固有频率分别下降9.82%，28.80%。

(2) 储液结构振动加速度沿壁板高度呈放大效应，地震动强度的提高使放大效应更加明显。相比于无水条件，储水条件下加速度传递系数对地震动强度的敏感性提高。同一等级地震动强度下，随着储液深度增加，结构加速度放大效应增强。

(3) 储液结构应变沿壁板高度呈现减速增大的趋势，壁板振动竖向振型符合悬臂梁剪切变形理论。储水条件下，壁板临水部分变形由于液体附加质量效应得到加强，无水部分变形相对弱化。结构变形随地震动增强而增加，结构顶部应变值的地震动强度敏感性较强。同一等级地震动强度下，储水深度的增加使结构变形幅度提高。

(4) 储液结构动水压力随水深增加呈现先增大后减小的趋势，相较于对流压力，脉冲压力是动水压力主要组成部分。分别以流固耦合理论方法和现行设计规范计算得到了水平地震作用下动水压力标准值，发现现有规范对地面式矩形不锈钢储液结构设计不利，结合理论方法修正了动水压力系数。推导了动水压力所致倾覆力矩的计算公式，并得到了倾覆力矩系数。

本文采用模型试验方法进行参数研究，并结合理论分析得到了一些结论。未来还需要对针对不同结构尺寸、形状等进一步研究，以扩充认知体系，得出更具普遍指导意义的结论。