联合载荷下改进的角接触球轴承拟静力学分析模型

王延忠，鄂世元，贾彦蓉，马新忠，谢斌

(1.北京航空航天大学，北京 100191；2.洛阳轴承研究所有限公司，河南 洛阳 471039；3.高性能轴承数字化设计国家国际科技合作基地，河南 洛阳 471039；4.河南省高性能轴承技术重点实验室，河南 洛阳 471039)

滚动轴承是机械领域广泛应用的基础零部件，角接触球轴承能同时承受径向、轴向载荷，且刚性及高速性能优越，在各类精密机械上广泛应用，其性能将直接影响主机的性能[1]。

国内外学者均采用拟静力学分析轴承的变形及载荷分布等[2-6]：文献[7]最先提出球轴承拟静力学模型，将沟道控制理论作为球运动的边界条件，使轴承运动非线性方程组存在唯一解，但模型求解速度慢，且计算结果存在一定的误差；文献[8]基于经验拖动力计算公式取代沟道控制理论改进拟静力学模型，计算结果误差较小，但模型求解速度慢。拟静力学模型多采用牛顿-拉弗森迭代法求解，迭代初值选取不当易导致计算结果收敛困难。随计算机技术的发展，文献[9]基于迭代变量之间的几何约束关系，由程序计算出合理的迭代初值，避免了迭代初值选取的盲目性；文献[10]提出了一种牛顿-拉弗森迭代法的改进算法，引入中间变量，减少了未知量数目，提高了计算速度；但上述模型均未考虑轴承内圈偏移对其受力平衡的影响。

针对上述模型的不足，考虑轴承内圈偏移对其受力平衡的影响，建立角接触球轴承拟静力学模型，在传统牛顿-拉弗森迭代求解的基础上引入对迭代初值的几何约束，并与传统算法对比验证优化算法的正确性。

1 角接触球轴承拟静力学模型

传统角接触球轴承拟静力学分析方法是在轴承静力学基础上，考虑球的离心效应、陀螺力矩和接触变形，计算得到某一瞬时轴承内部载荷分布、球转速、内圈位移等。由于轴承运动状态复杂，为简化计算，建立拟静力学分析模型时通常做以下假设：1)球轴承符合刚性套圈假设；2)可以采用沟道控制理论建立球与内、外圈之间的运动关系；3)忽略球沿运动方向的作用力以及内圈、球与保持架之间的相互作用；4)不考虑球与内、外圈之间的润滑。

轴向载荷一般通过套圈或与轴承相连的轴的轴肩周向施加，理论计算中将其等效为轴向载荷Fa、径向载荷Fr(通过轴传递给内圈的径向载荷)以及倾覆力矩M(轴向载荷施加过程中可能存在的偏心现象而产生的力矩)，如图1所示。

1.1 单个球的几何变形协调方程

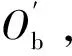
Δij=Dw(fi-0.5)+δij，

(1)

Δej=Dw(fe-0.5)+δej，

(2)

式中：fi，fe分别为内、外圈沟曲率半径系数；Dw为球直径；δij，δej分别为球与内、外圈的接触变形量；ri，re分别为内、外圈沟道半径。

内、外圈沟曲率中心的轴向、径向距离分别为

A1j=Asinα0+δa+risinθcosφj，

(3)

A2j=Acosα0+δrcosφj-Ri(1-cosθ)cosφj，

(4)

A=ri-re-Dw，

α0=arccos(1-Gr/2A)，

Gr=Di-De-2Dw，

φj=2π(j-1)/Z，

式中：A为内、外圈沟曲率中心距；α0为初始接触角；δa，δr，θ分别为内圈的轴向位移、径向位移和倾角；Gr为径向游隙；Di，De分别为内、外圈沟底直径；φj为第j个球方位角；Z为球数。

根据几何关系可知，第j个球与内、外圈的接触角可表示为

(5)

(6)

(7)

(8)

式中：X1j，X2j分别为球与外圈沟曲率中心的轴向距离和径向距离。

由(1)～(8)式可得单个球的几何变形协调方程为

(9)

(A1j-X1j)2+(A2j-X2j)2-

[Dw(fi-0.5)+δij]2=0。

(10)

1.2 球受力平衡方程

根据沟道控制理论，当轴承高速运转时，球受离心力作用会与内圈分离，陀螺力矩完全由球与外圈的摩擦力平衡。球受力示意图如图4所示，受力平衡方程为

(11)

式中：Qij，Qej分别为球与内、外圈的接触载荷；Mg j为球所受陀螺力矩；Fcj为球所受离心力；λij，λej为修正系数，随载荷变化，且λij+λej=2；ωm为球公转角速度；ωR为球自转角速度；ω为内圈角速度；Dpw为球组节圆直径；J为球转动惯量；m为球质量；β为球姿态角。

1.3 内圈受力平衡方程

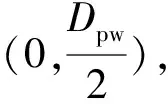
xwj=X1j-Dw(fe-0.5)sinα0，

(12)

(13)

考虑内圈质心从(0，0)移动至(δa，δrcosφj)，球与内圈接触点的坐标为

(14)

(15)

第j个球对内圈的作用力矩对应的力臂hj为

(xij-δa)tanαijsinαij,

(16)

内圈受力平衡方程组为

(17)

2 牛顿-拉弗森迭代法的初值约束

上述模型通常采用牛顿-拉弗森(N-L)迭代法求解，但易因迭代初值选取不当导致计算结果收敛困难，在此基于轴承几何关系约束初值[10]。该算法迭代包括δa，δr，θ和球心与外圈沟曲率中心的位置关系X1j，X2j。由图2几何关系可知，球与内、外圈的接触变形量δij，δej均为正值，以此约束X1j，X2j初值，X1j，X2j初值应满足Δij>Dw(fi-0.5)，Δej>Dw(fe-0.5)，即球心位于以外圈沟曲率中心为圆心，半径为Dw(fe-0.5)的圆和以内圈沟曲率中心(A1j，A2j)为圆心，半径为Dw(fi-0.5)的圆之外，如图6所示。

以(0.5A1j，0.5A2j)为初始点，上述两圆会出现相交的情况，将初始点沿与内、外圈沟曲率中心连线的垂直方向向上平移，得到新的初始点，判断其是否在两圆内，并循环直至得到合适的初始点。轴承拟静力学分析模型算法流程图如图7所示。

3 实例分析

以NSK 7016A5角接触球轴承为例进行分析，其主要结构参数见表1。轴向载荷为3 500 N,径向载荷为88.5 N[11]。

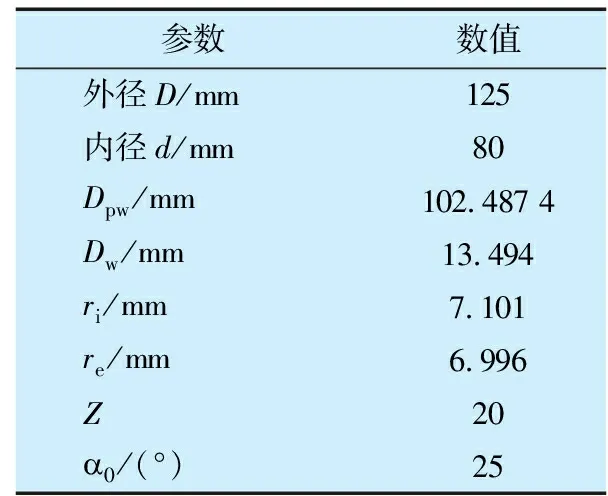
表1 7016A5角接触球轴承主要结构参数

当转速为8 000 r/min时，收敛精度相同的情况下，优化前、后的算法计算结果见表2，优化后的算法迭代次数少，且规避了因初值选取不当而导致算法收敛困难的问题，使角接触球轴承非线性方程组的求解速度进一步加快。

表2 优化前、后的算法对比

在Fa=3 500 N，Fr=88.5 N的联合载荷下，不同方位角的球与沟道的接触角、接触载荷随转速的变化分别如图8、图9所示：1)随转速升高，内圈接触角增大，外圈接触角减小；2)不同方位角的球与套圈的接触载荷不同，方位角为0°的球与套圈的接触载荷最大；3)随转速升高，内圈接触载荷减小，外圈接触载荷增大。

4 结束语

针对传统角接触球轴承拟静力学分析模型的不足，考虑轴承内圈偏移对其力学平衡的影响，建立轴承拟静力学分析模型，在牛顿-拉弗森迭代法求解的基础上引入了对迭代初值的几何约束，选取合适的初值，解决了因初值不当导致算法收敛困难的问题，并提高了计算速度。文中方法可为该类轴承的设计和分析提供参考。