不同沟形七沟道球笼式等速万向节钢球周向力和法向接触力分析

谢鲲,丁新,刘征宇

(上海应用技术大学 轨道交通学院，上海 201418)

万向节是一种能实现扭矩传输的部件，扭矩从输入轴传入，经星形套作用于钢球，再由钢球作用于钟形壳上，从而实现扭矩传递。六沟道球笼式等速万向节作为应用广泛的等速万向节，前人对其内部受力进行了分析：文献[1-2]对球笼式等速万向节内部接触应力进行分析，结果表明将椭圆形沟道改为圆弧形沟道可缓解应力集中问题；文献[3]建立圆弧形、双心弧形、椭圆形沟道的等速万向节三维模型，基于ANSYS对其承受极限转矩时的滚道接触应力进行分析，结果表明不同沟形内、外沟道接触应力不同。

关于七沟道球笼式等速万向节的研究较少，文献[4]基于七沟道球笼式等速万向节钢球受力模型，得到了钢球在星形套内沟道和钟形壳外沟道运动时沟道对钢球的周向力、法向接触力，并基于ADAMS进行动力学分析，结果表明七沟道球笼式等速万向节钢球的周向力、法向接触力均小于六沟道球笼式等速万向节；但其仅研究了一种沟道，沟形不同，在相同条件下钢球的周向力、法向接触力不同，进而影响球笼式等速万向节的性能，故有必要分析不同沟形七沟道球笼式等速万向节钢球的周向力、法向接触力。本文推导了不同沟形七沟道球笼式等速万向节钢球的周向力和法向接触力的计算公式，并与ADAMS仿真结果进行对比。

1 七沟道球笼式等速万向节钢球周向力和法向接触力理论分析

钢球在星形套内沟道和钟形壳外沟道内运动，如图1所示，ρN=[ON,i′，j′，k′]为以星形套曲面中心ON为原点，以星形套输入轴IN为j′方向的固定坐标系，ρW=[OW,i，j，k]为以钟形壳曲面中心OW为原点，以钟形壳输出轴IW为j方向的固定坐标系，建立ρW相对于ρN的方向矩阵，αi为向量i′与向量i的夹角，即

cosαi=cos(-δ)cosδ-sin(-δ)cos(2θ)sinδ，

(1)

式中：δ为星形套输入轴转角；θ为星形套输入轴与钟形壳输出端之间轴间夹角的一半。

各个钢球的瞬时受力随转角δ和轴间夹角2θ变化而变化，则七沟道球笼式等速万向节钢球所受周向力QN为

(2)

式中：MN为传递的扭矩；R为沟道圆弧半径；g为重力加速度；α为接触角；φ为半锥角。

通过方向矩阵建立钢球法向接触力QNQ与所受周向力QN之间的关系[5]，如图2所示，即

[cos(-δ)cosδ-sin(-δ)cos(2θ)sinδ]。

(3)

分析万向节几何模型，得到其曲面参数与万向节结构参数的关系[6]，如图3所示，O为沟曲率中心；O1为钢球中心。

对于椭圆形沟道

(4)

(5)

周向力为

(6)

法向接触力为

[cos(-δ)cosδ-sin(-δ)cos(2θ)sinδ]，

(7)

式中：a为接触椭圆长半轴；b为接触椭圆短半轴；f为沟曲率半径系数；β为压力角；Dw为钢球直径。

对于双心弧形沟道

R=fDw，

(8)

(9)

(10)

(11)

[cos(-δ)cosδ-sin(-δ)cos(2θ)sinδ]。

(12)

对于圆弧形沟道

R=fDw，

(13)

(14)

圆弧形沟道等速万向节传递扭矩时，沟道直径大于钢球直径，钢球与内、外沟道仅两点接触，不同于双心弧、椭圆沟道。星形套传递扭矩的力臂L1小于钟形壳力臂，法向接触力由接触角α、轴间夹角的一半θ、转角δ决定[7]，钢球在沟道中受到的周向力为

(15)

法向接触力为

[cos(-δ)cosδ-sin(-δ)cos(2θ)sinδ]，

(16)

式中：Rg为钢球回转中心半径。

2 七沟道球笼式等速万向节钢球周向力和法向接触力仿真分析

2.1 建模

以某七沟道球笼式等速万向节为研究对象，其主要结构参数见表1。在SOLIDWORKS中建立椭圆形、双心弧形、圆弧形沟道万向节几何模型，并导入ADAMS中，其中椭圆形沟道等速万向节轴间夹角为30°的三维模型如图4所示。在星形套和钟形壳上分别施加旋转副约束，以星形套或钟形壳转动轴线为旋转副轴线，万向节中心为旋转副中心。根据万向节内部约束关系，并根据接触力形式[8]在星形套、钟形壳、保持架、钢球之间施加接触力，摩擦力为库仑摩擦力，静摩擦因数为0.005，动摩擦因数为0.002。

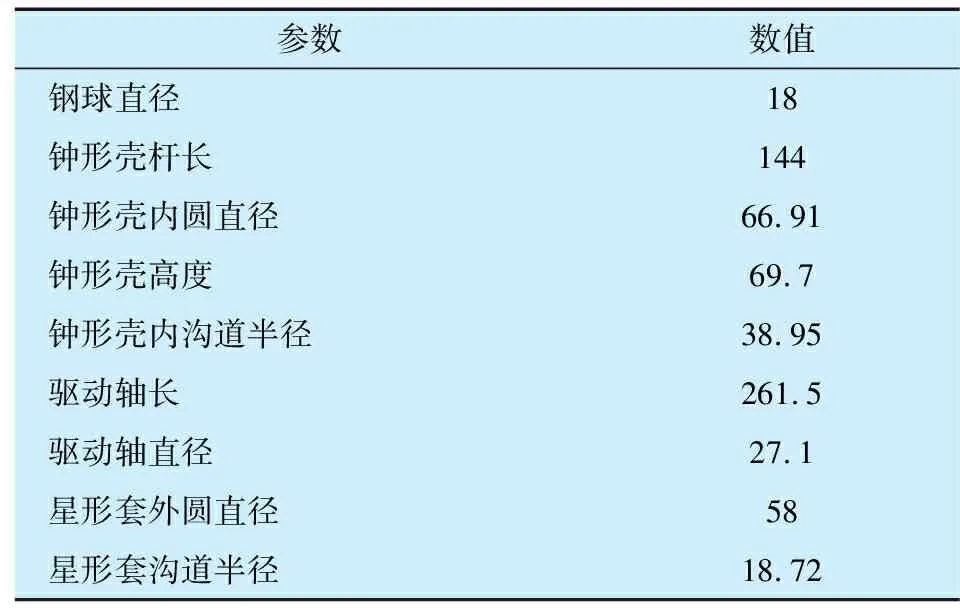
表1 七沟道球笼式等速万向节主要结构参数

2.2 模型验证

在一定范围内的转角下，球笼式等速万向节钢球始终位于输入端星形套内沟道和输出端钟形壳外沟道夹角的平分线上[9]，主从动轴角速度不变，即等速性。轴间夹角为30°，输入轴扭矩为100 N·m时星形套和钟形壳角速度如图5所示，星形套和钟形壳角速度近似相等，说明了模型的正确性。

2.3 结果分析

输入轴扭矩分别为100，200 N·m时，不同沟形七沟道球笼式等速万向节钢球周向力和法向接触力的变化规律分别如图6、图7所示。

由图6、图7可知：

1)钢球周向力和法向接触力理论计算值与ADAMS仿真值相差不大，进一步说明了仿真模型的正确性。

2)圆弧形沟道钢球的周向力和法向接触力明显小于椭圆形、双心弧形沟道，当轴间夹角为0°，15°，30°时，钢球周向力和法向接触力从大到小依次均为双心弧形、椭圆形、圆弧形。

3)在万向节输入扭矩相同时，随轴间夹角增大，钢球周向力和法向接触力逐渐增大。

4)在万向节的轴间夹角相同时，随扭矩增大，钢球周向力和法向接触力逐渐增大。

3 结论

建立了不同沟形七沟道球笼式等速万向节钢球周向力和法向接触力理论计算和仿真分析模型，并分析了输入轴扭矩分别为100，200 N·m时不同轴间夹角下钢球周向力和法向接触力的变化规律，得出以下结论：

1)钢球周向力和法向接触力理论计算和仿真分析结果均一致，说明了模型的正确性；

2)随输入轴扭矩和轴间夹角增大，钢球周向力和法向接触力增大；

3)圆弧形沟道钢球周向力和法向接触力明显小于椭圆形和双心弧形，随轴间夹角或扭矩增大，圆弧形沟道钢球周向力和法向接触力与椭圆形、双心弧形差距也增大。