比较：让学生的概念认知趋于结构化比较：让学生的概念认知趋于结构化——以“分数的意义”为例

◎陈 城

(南京市百家湖小学，江苏 南京 210000)

心理学家布鲁纳指出,学习的实质在于主动形成认知结构.认知结构化是指教师整体布局，学生认知经历比较、关联，化零碎认识为整体认知结构.从布鲁纳提倡的建立“学科基本结构”理念，到奥苏泊尔提出的所学与认知结构相联系的有意义学习理论，都与笔者研究的“结构”存在联系.比较作为一种学习方法，常常用于对知识的整体性的认识和建构，通过比较，学生在“不同”中看到“联系”，在“解构”中进行“建构”.概念认知是指学习主体对概念形成自己的认知与理解.让学生对数学概念产生结构化的认知，是数学教师追求的目标，若想达成这一目标，教师有必要根据概念实质，引导学生在学习过程中进行比较.下面，笔者结合苏教版五年级下册的“分数的意义”，展开结构化研究：

一、比较的缘由

“分数的意义”是苏教版五年级下册内容，在此之前，学生已经在三年级学习了“认识一个物体的几分之几”与“认识一些物体的几分之几”，初步了解了分数的意义，并系统学习了除法、倍数等相关联的知识.学生五年级学习这一课的时候，已经积累了足够的前概念和生活经验，但这些知识与经验都零散地存放于学生的脑海里，等待在进一步的学习中，通过比较产生关联，形成结构化.这里，需要教师注意以下这几个地方：一是对单位“1”的概念认知，“1”是学生幼儿时就接触的数，概念内涵丰富，这里的单位“1”与过去学过的“1”有什么区别和联系呢？学生通过比较后，能够感悟单位“1”是一种倍比关系中的比较标准，而不是数的组成中的计数单位.二是对分数的概念认知，分数既可以表示“量”，也可以表示“率”，但核心还是在“率”，理解分数的关键在于理解分数表示了两个数量之间的倍比关系，与所学的除法、倍数存在着很大的关联.理解到这一点，学生才能感悟到分数的实质，有利于他们接下来学习假分数、带分数等一系列的概念，而这需要教师在课堂教学中，通过设置相应的比较环节，让学生自主发现并理解.

二、具体策略

(一)在冲突处比较，让“1”的概念认知趋于结构化

这里的冲突是指认知的冲突，新知识和学生原有知识发生矛盾，进而打破学生的认知平衡，对学生的认知进行调整、整合，从而建立新的认知平衡.在教学实践中，学生经常会遇到知识的冲突，这时，教师要引导学生在冲突处比较，在比较中厘清概念的发展，让认知趋于结构化.例如以下环节：

师:看到“1”你能想到什么？

生：一个人，一棵树.

师：你们想到的“1”，都是指数量.如果把○看作1，那○○○○是？

生：4.

师：如果把○○看作1，那这里的○○○○是？

生：是2.因为把○○看作1组，○○○○就有2组，所以是2.

师：如果把○○○○○○○○看作1，那○○○○是多少？

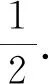
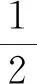
生1：因为每组下面的那个“1”都是不一样的.

生2：第一组的“1”表示1个，第二组的“1”表示1份，2个，第三组的“1”表示一份，8个.

生3：1可以看作一个整体.

师：看来，“1”不再是我们以前单纯认为的数量1，可以说它表示1份、一个整体，那从刚才比较的过程来看，这里的“1”相当于？

生：比较的标准.

学生在一年级时就认识了“1”，建立了无论1棵数，还是1个人，只要在数量是1，都可以用1表示.二年级的时候，学生学习了乘法，初步感知1份、1组的概念，但对“1”的认识更多地停留在指数量1上.本环节，教师应引导学生在冲突处进行比较，学生的目光聚焦到“1”上，在比较中关注到“1”的不同，对“1”的概念的认知也从数量1，上升到更概括的认知——1份或1组，由此可见，这里的“1”实际上相当于一种比较的标准.至此，学生对“1”的概念认知愈加趋于结构化，也为后面理解分数意义、分数的基本性质、倍率与分率的关系打下基础.

(二)在回顾处比较，让单位“1”的概念趋于结构化

学生是带着自己原有的理解与认识来到课堂的，因此，教师一定要充分了解学生原有的旧知与经验，充分利用学生的旧知，以旧知为生长点，让学生进行新旧知的比较，实现认知的同化或顺应，促使新旧认知结合，让知识趋于结构化.例如，单位“1”的概念，很多教师只是告知学生什么是单位“1”，这样简单的告知，剥夺了学生的认知体验，不利于学生形成结构化的认识，笔者在教学中是这样处理的：

师：我们知道“1”代表一种比较的标准，在以往学过的知识里，你觉得有哪些知识也表示比较的标准？

生1：长度单位，比如1 cm，1 dm，1 m.

生2：面积单位，比如1 cm2.

师：我们把1 cm请出来，这是1 cm，那这条线段的长度是？

生：将它和1 cm比较，有几个1 cm就是几厘米.

师：如果这个图形的面积是1 cm2，那右边图形的面积怎么求？

生：将其和1 cm2比，我发现几个1 cm2合起来就是几平方厘米.

师：长度单位、面积单位，它们都是计量单位.看来，刚刚我们说的这个比较的标准，其实是单位，那么我们之前说的1，可以叫作单位“1”.

师：回顾刚才讲的关于○的题，每组是把什么看作了单位“1”？

生：先是把一个○看作了单位“1”，然后是把一些○，相当于一个整体看作了单位“1”.

师：是的，现在我们发现，可以把什么看作单位“1”？

生：一个物体、一个整体，还有计量单位，它们都可以看作单位“1”.

师：比较一下原来学过的“单位”，和今天学的“1”和单位“1”，你们有什么想说的？

生1：把单位，还有“1”合起来，就是我们学的单位“1”.

生2：单位“1”和单位类似是一种比较的标准.

师：数学上把平均分的对象，比如一个物体、一个计量单位或由许多物体组成的一个整体，都可以用自然数1来表示，通常，我们把它叫作单位“1”.

师：(指着图中椭圈内的一个实心圆)这个实心圆可以用自然数1表示吗？(生：能！)那在这里它能表示单位“1”吗？为什么？

生：不能，因为这里分的并不是它，分的是这6个圆，单位“1”是6个圆组成的整体.

生：要把平均分的对象看作单位“1”.

师：现在，你们感受到自然数1和单位“1”的区别了吗？

单位“1”的本质还是单位，是一种比较的标准.但学生在理解与归纳的过程中，更多的时候只关注了“1”，而忽略了其中的“单位”二字.什么是单位？单位是测量比较中的标准量，没有比较，也就没有单位，确立的单位，必然被视为“1”.教师让学生回顾旧知：还有哪些学过的知识，也是一种比较的标准？学生的认知一下子被打开，能够自主激活认知结构中的旧知，原有的长度单位、面积单位、重量单位等旧知迅速被提取出来.这里，教师注重引导学生将新旧知进行对比，学生对单位“1”不再陌生，有了旧知“单位”和新知“1”的支撑，教师在揭示单位“1”的概念后，又出示一幅图，让学生感受一个实心圆可以用数1来表示，但是不可以用单位“1”表示，单位“1”是在比较中产生的，而这幅图是将整体进行平均分，因而要把6个圆组成的一个整体看作单位“1”，让学生彻底弄清数“1”和单位“1”的联系与区别，从而形成结构化的认识.

(三)在迁移处比较，让分数的概念认知趋于结构化

迁移是一种学习对另一种学习的影响.学习之所以能发生迁移是因为知识间存在某些共同的元素，这些共同的元素恰恰是知识的本质与关键所在.教师不仅要创设条件促使学生的迁移得以发生，更重要的是要引导学生在迁移的过程中进行比较，从而淡化外在形式，抓住关键本质.在概念教学中，学生经历在迁移中比较后，更容易概括出概念的本质，在大脑中逐步形成一个具有内部规律的整体结构.例如以下分数概念的学习：

师：如果把6个梨看作单位“1”，这2个梨怎么表示？

师：如果把这3段线段看作单位“1”，这一段是？

生：把单位“1”平均分成n份，取m份.

师：数学上，我们可以说是平均分成若干份.

师：那你觉得，到底什么是分数？

生：把单位“1”平均分成若干份，表示这样一份或几份的数，叫分数.

师：没错，把单位“1”平均分成若干份，表示这样一份或几份的数，就叫分数，表示其中一份的数，叫作分数单位.比较单位“1”和分数单位，它们的意思一样吗？

生：不一样，虽然都有单位两个字，把谁平均分，谁就是单位“1”.分数单位只是其中的一份.

师：是的，分数单位就如同过去学的计数单位，通过累积，得到对应的几分之几.而单位“1”是比较的标准，通过把单位“1”平均分，得到对应的几分之几.

(四)在变式中比较，让概念的关系认知趋于结构化

变式是认识概念本质的一种教学手段，教师可以在教学过程中保留概念的本质特征，改变非本质特征，让学生对概念的本质特征形成更深刻的认识.在教学中，教师不仅要让学生感受到变式，更应引导学生在变式中进行比较，感受变中的“不变”，从而抓住关键与本质.在“分数意义”这一课的教学中，很多教师没有帮助学生厘清分数的概念实质，没有沟通分数与倍数的关系，导致学生无法将分数与之前的知识产生关联，无法形成结构化的认知.以下的做法值得借鉴：

(师出示下图)

师：如果把第一排的1个圆看作单位“1”，下面两排分别用什么数表示？

生：两个单位“1”，用2表示，最后一排用4表示，因为是4个单位“1”，相当于第一排的4倍.

师：为什么都用了整数来表示？

生：下面两排都相当于几个单位“1”.

师：如果把第三排4个黑圆看作单位“1”，上面第一、第二排用什么数表示？

师：这次为什么都用分数表示？

生：因为4个黑圆是单位“1”，上面的两排表示把单位“1”平均分.

师：如果把第二排两个○看作单位“1”，第一、第三排分别用什么数表示？

师：为什么第一排用分数表示，第三排用整数表示呢？

生：2个○是单位“1”时，上面一排表示平均分，把单位“1”平均分成2份，取其中一份.而下面4个黑圆相当于2个单位“1”，用2表示.

(师出示下图)

师：下面分析一下上述我们解决的问题中，有什么不同点和相同点？先独立思考，再小组讨论.

生：有的是把1个○看作单位“1”，有的是把2个○或4个○看作单位“1”.

生：同一排，比如第二排，表示的形式不一样.

师：是的，将同一个量和不同的单位“1”进行比较，会有不同的表示形式.

师：那有什么相同点呢？

生：有的用整数表示几倍，不是整倍数的就用分数表示.

师：是的，这里不管是用整数还是用分数，都表示了它与单位“1”的倍比关系.

教师出示三组富有变式的问题，即每次改变单位“1”的对象，但不变的是分数、整数与单位“1”之间的关系，从而突出本质.第一问把第一排看作单位“1”，求下面两排，学生在比较中意识到几个单位“1”用整数几来表示；第二问把第三排4个黑圆看作单位“1”，求上面两排，学生在比较中意识到把单位“1”平均分，表示这样的几份用分数.最后，把第二排的2个圆看作单位“1”，求其余两排.通过变式的比较，学生能够清晰地建立分数、整数倍、单位“1”三者的关系，当教师抛出问题“比较一下上述我们解决的问题，有什么不同点和相同点？”时，学生能在比较中得出，不管用整数还是用分数，都表示它与单位“1”的倍比关系，从而认识分数的本质，并与已经学过的倍数关系产生了关联，构建了完整的倍比关系知识网络，形成了完整的认知结构.另外，这里的以圆进行比较，不再是部分与整体的比较，而是两个独立量之间的比较，这样的比较有利于学生在接下来的学习中再一次突破自己的认知结构，更好地理解并接纳假分数的概念.